A fraction shows the equal parts of a collection or whole. The number line is a straight line with numbers placed at equal intervals along its length. Representing Fractions on Number Line means pointing the fractions on the number line. It shows the interval between two numbers. Learn the process of how to represent fractional numbers on a number line from the below-provided segments of this page.
Representing Fractions on Number Line – Definition
First of all, representing whole numbers on a number line means pointing those numbers on the line. In the same way, we need to point to the fraction which is between two numbers on the number line. Here, we need to divide the space between two whole numbers on a number line into the number of parts. Make each part as a fraction and then point to the respective fraction.
Examples of Fractions are \(\frac { 2 }{ 5 } \), \(\frac { 1 }{ 2 } \), \(\frac { 5 }{ 6 } \).
How to Represent Fraction on Number Line?
Are you looking for any help on representing fractions on a number line then read the following points. Here you will get the detailed step-by-step procedure.
- Get the fraction and draw a number line.
- If the numerator of the fraction is more than the denominator, then convert the fraction into a mixed fraction.
- Divide the space between two consecutive whole numbers and the denominator number of parts.
- And consider each division as a fraction.
- Now, mark the points on the number line.
Also, Read More Related Articles
Representing Fractions on a Number Line Examples
Example 1:
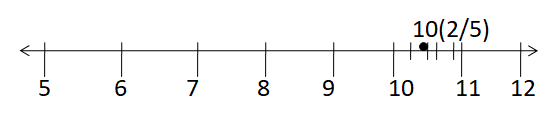
Represent \(\frac { 52 }{ 5 } \) on the number line.
Solution:
First, convert \(\frac { 52 }{ 5 } \) into the mied fraction.
\(\frac { 52 }{ 5 } \) = 10\(\frac { 2 }{ 5 } \)
Now, we start from 10 and divide the section between 10 and 11 into 5 equal parts because the denominator is 5. The second point in the division is 2/5. Mark the point as 10\(\frac { 2 }{ 5 } \).
Example 2:
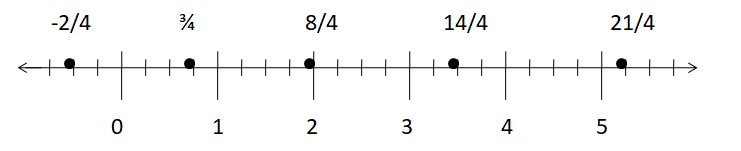
Draw a number line to represent the fractions –\(\frac { 2 }{ 4 } \), \(\frac { 3 }{ 4 } \), \(\frac { 8 }{ 4 } \), \(\frac { 14 }{ 4 } \), and \(\frac { 21 }{ 4 } \).
Solution:
Given fractions are –\(\frac { 2 }{ 4 } \), \(\frac { 3 }{ 4 } \), \(\frac { 8 }{ 4 } \), \(\frac { 14 }{ 4 } \), and \(\frac { 21 }{ 4 } \)
The denominator of all the factions is 4. So, divide each interval into 4 parts. Each part so obtained will represent the fraction 1/4 and the number line obtained will be in the form of as shown here.

To mark –\(\frac { 2 }{ 4 } \); move two parts on the left-side of zero.
To mark \(\frac { 3 }{ 4 } \); count three parts from the zero.
To mark \(\frac { 8 }{ 4 } \); count 8 parts from the zero.
To mark \(\frac { 14 }{ 4 } \); count 14 parts from the zero.
To mark \(\frac { 21 }{ 4 } \), count 21 parts from the zero.
The following diagram shows markings of fractions –\(\frac { 2 }{ 4 } \), \(\frac { 3 }{ 4 } \), \(\frac { 8 }{ 4 } \), \(\frac { 14 }{ 4 } \), and \(\frac { 21 }{ 4 } \) on a number line.
Example 3:
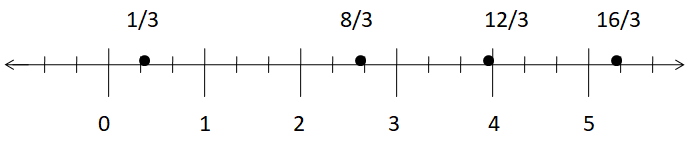
Represent the fractions \(\frac { 1 }{ 3 } \), \(\frac { 12 }{ 3 } \), \(\frac { 16 }{ 3 } \), \(\frac { 8 }{ 3 } \) on a number line.
Solution:
The given fractions are \(\frac { 1 }{ 3 } \), \(\frac { 12 }{ 3 } \), \(\frac { 16 }{ 3 } \), \(\frac { 8 }{ 3 } \)
The denominator of all the factions is 3. So, divide each interval into 3 parts. Each part so obtained will represent the fraction 1/3 and the number line obtained will be in the form of as shown here.

To mark \(\frac { 1 }{ 3 } \), move 1 point on the right side of zero.
To mark \(\frac { 12 }{ 3 } \), move 12 pionts on the right side of zero.
To mark \(\frac { 16 }{ 3 } \), move 16 points on the right side of zero.
To mark \(\frac { 8 }{ 3 } \), move 8 points on the right side of zero.
The following diagram shows markings of fractions \(\frac { 1 }{ 3 } \), \(\frac { 12 }{ 3 } \), \(\frac { 16 }{ 3 } \), \(\frac { 8 }{ 3 } \) on a number line.
Example 4:
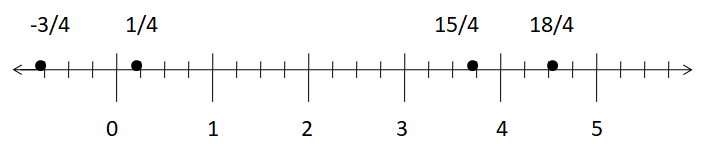
Represent the fractions \(\frac { 15 }{ 4 } \), \(\frac { 1 }{ 4 } \), \(\frac { -3 }{ 4 } \), \(\frac { 18 }{ 4 } \) on a number line.
Solution:
The give fractions are \(\frac { 15 }{ 4 } \), \(\frac { 1 }{ 4 } \), \(\frac { -3 }{ 4 } \), \(\frac { 18 }{ 4 } \)
The denominator of all the factions is 4. So, divide each interval into 4 parts. Each part so obtained will represent the fraction 1/4 and the number line obtained will be in the form of as shown here.

To mark –\(\frac { 3 }{ 4 } \); move three parts on the left-side of zero.
To mark \(\frac { 1 }{ 4 } \); count one part from the zero.
To mark \(\frac { 15 }{ 4 } \); count 15 parts from the zero.
To mark \(\frac { 18 }{ 4 } \), count 18 parts from the zero.
The following diagram shows markings of fractions \(\frac { 15 }{ 4 } \), \(\frac { 1 }{ 4 } \), \(\frac { -3 }{ 4 } \), \(\frac { 18 }{ 4 } \) on a number line.
FAQ’s on Representing Fractions on Number Line
1. How do you represent a fraction on a number line?
To represent fractions on the number line, divide each line segment between 0 to 1 into the denominator number of parts. And count the numerator parts from zero and mark the fractions.
2. What is \(\frac { 3}{ 4 } \) on a number line?
The fraction \(\frac { 3}{ 4 } \) means 3 out of 4 equal parts. So, count 3 parts from 0 on the number line to get \(\frac { 3}{ 4 } \).
3. What does the denominator of a fraction represent on the number line?
A fraction has two parts numerator and denominator. The denominator means how many equal parts an item was divided into.
