If two or more figures in equal measure or the same due to their shape, then this property is called as a similarity. When we magnify or demagnify similar figures, they always superimpose each other. Check the condition of similarity, similarity applications and solved problems in the following sections.
What is Similarity?
When two or more objects appear the same or equal because of their shape, this property is known as a similarity. When we magnify or demagnify similar figures, they always superimpose to each other. One of the examples is of two circles of any radii are always superimpose each other because they are similar. In the same way, the two squares are also always similar.
- Enlargement Transformation
- Reduction Transformation
- Properties of size Transformation
- Similar Triangles
- Criteria of Similarity between Triangles
- AA Criterion of Similarity
- Basic Proportionality Theorem
- Converse of Basic Proportionality Theorem
- Application of Basic Proportionality Theorem
- Greater segment of the Hypotenuse is Equal to the Smaller Side of the Triangle
- AA Criterion https://ccssanswers.com/of Similarly on Quadrilateral
- Pythagoras’ Theorem
- Converse of Pythagoras’ Theorem
- Applying Pythagoras’ Theorem
- Riders Based on Pythagoras’ Theorem
Criteria of Similarity
If two-dimensional figures are similar, then all the corresponding angle pairs are equal or all corresponding sides are proportional. These are different rules to say that two triangles are similar.
SSS Similarity Criterion
The SSS similarity criterion states that if three sides of one triangle are proportional to the three sides of another triangle, then they are similar. It means that those triangles are equiangular also.
The following triangles ABC, DEF are similar as their corresponding sides are proportional.

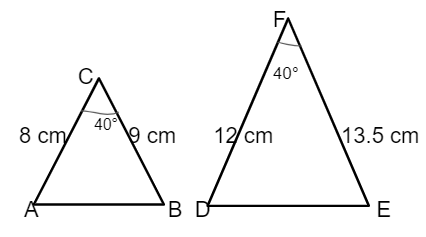
SAS Similarity Criterion
It states that if two sides of one triangle are proportional to the corresponding two sides of the second triangle, and the included angles are equal, then the two triangles are said to be similar.
AA Similarity Criterion
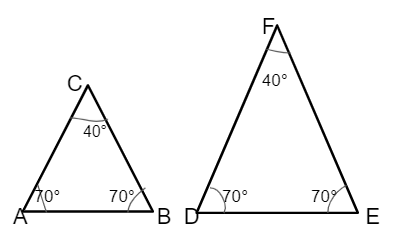
It states that if three angles of one triangle are equal to the three angles of the other, then the two triangles will be similar.
In the following figure, ∠A = ∠D, ∠B = ∠E, ∠C = ∠F.
Applications of Similarity
The applications of similarity are listed here.
- It is helpful to solve problems involving distance and height.
- The similarity is widely used in architecture.
- Solving mathematical problems involving triangles.
Similarity Vs Congruency
The main difference between similarity and congruency are provided in the following sections.
| Similar | Congruent |
|---|---|
| Figures should have the same shape. | Figures should have the same shape and size. |
| Objects can have different sizes. | Objects must have the same size. |
| The sides of the figures have the same proportions. | Figures are completely same in all aspects. |
| They are resized versions of each other. | They are identical to each other. |
| Objects are may or may not be congruent to each other. | Objects are also similar to each other. |
Solved Questions on Similarity
Question 1:
It is given that △DEF ~ △MNK. If DE = 5, MN = 6, find Area of △DEF/Area of △MNK.
Solution:
Given that,
DE = 5, MN = 6
△DEF ~ △MNK
So, \(\frac { Area of △DEF }{ Area of △MNK } \) = \(\frac { DE² }{ MN² } \)
= \(\frac { 5² }{ 6² } \)
= \(\frac { 25 }{ 36 } \)
Question 2:
Check whether two triangles are equal.
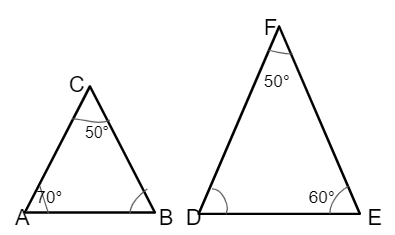
Solution:
The sum of all internal angles in a trinagle is 180 degrees.
In triangle ABC,
∠A + ∠B + ∠C = 180°
∠B + 70° + 50° = 180°
∠A = 180° – 120°
= 60°
In triangle DEF
∠D + ∠E + ∠F = 180°
∠D + 60° + 50° = 180°
∠D = 180° – 110°
= 70°
So, ∠D = ∠A and ∠B = ∠E
Using AA rule, ΔABC ~ ΔDEF.
FAQ’s on Similarity of Triangles
1. What are the rules of similarity?
The three rules of similarity are SSS similarity, SAS similarity, and AA or AAA similarity.
2. What is a similarity statement?
A similarity is a statement used in geometry to prove exactly two shapes have the same and are in equal proportion.
3. How is similarity used in real life?
The similarity is used in designing, solving the problems involving distance, height and etc.
4. What is the AA similarity theorem?
The AA criterion for triangle similarity states that if three angles of one triangle are equal to the three angles of the other, then two triangles are similar.