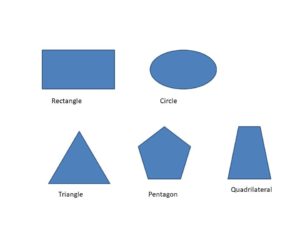
The images or shapes that are closed by the line or line-segment are called simple closed curves. A Closed curve’s starting point and ending points are the same and a closed curve doesn’t cross its path. Triangle, quadrilateral, circle, pentagon, …etc. are an example of the simple closed curves.
Simple closed curves are
Generally, curves are generated with the line only. By using the line or line segments only, we can draw the number of curves.
Types of Curves
Different types of curves are there. They are
1. Simple Open Curves
2. Closed curves
3. Non – Simple Curve
4. Upward curve
5. Downward curve
1. Simple Open Curves
Simple open curves are created with the line-segment but there is no intersection itself. That means, there is no joining point between the starting point and ending point.

2. Closed Curves
Closed curves are opposite to open curves. In closed curves, line intersection will be done. That means the starting and ending points are joined at the same point.

Also, See:
3. Non-Simple Curves
A Non-simple curve is a little bit typical compared to simple curves and it crosses its path while joining the ending point of the curve with the starting point. Again non-simple curves are divided into two types. They are
1. Non-simple closed curves
2. Non-simple open curves

4. Upward Curve
Every curve is designed with a starting point and ending point. Where the two points starting and ending points are located in the upward direction is called as ‘Upward Curve’.

5.Downward Curve
The Downward curve is opposite to the Upward curve. The two points of the curve, starting and ending points are located in the downward direction are called as ‘Downward Curve’.

Simple Closed Curves Examples
Find which of the following are simple closed curves?

From the above diagram, we have four images.
Closed curves intersect themselves and there is no intersection point in open curves. In the above diagram, Figure a and d are closed curves.
