In the previous articles, we have discussed about slope and y-intercept, plotting points in the XY plane, independent variables and dependent variables, etc. Let us learn how to solve the slope of the graph y = mx + c from this page. In addition that you can find the problems on the slope of the graph y = mx + c in the below section.
Also Read:
- Problems on Slope and Y-intercept
- Worksheet on Slope and Y-intercept
- y-intercept of the Graph of y = mx + c
Introduction to Slope-Intercept Form | y=mx+c Equation of Straight Line Slope
y = mx + c is an equation of the line having a slope and y-intercept of the line in coordinate geometry. m represents the slope or gradient of the line and c is the y-intercept that cuts the point on the y-axis. The line cuts the y-axis at the point (0, c) which is the distance from the origin to the point c.
m = (y – c)/(x – 0)
m = (y – c)/x
mx = y – c
mx + c = y
y = mx + c
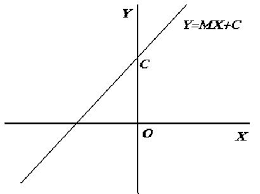
y = mx + c Straight Line Graphs Slope Examples
Example 1.
What is the slope of the equation 6x – 4y + 5 = 0?
Solution:
Given that the equation is
6x – 4y + 5 = 0
4y = 6x + 5
y = 6/4x + 5/4.
y = 3/2x + 5/4
Comparing the equation with y = mx + c,
we have m = 3/2.
Therefore, the slope of the line is 3/2
Example 2.
Find the equation of a line in the form of y = mx + c, having a slope of 4 units and an intercept of -6 units.
Solution:
Given that
The slope of the line, m = 4 and The y-intercept of the line, c = -6.
We know that
The slope-intercept form of the equation of a line is y = mx + c.
From the equation
y = 4x – 6
Therefore the required equation of the line is y = 4x – 6
Example 3.
Convert the equation 5x + 4y = 12 into y = mx + c and find its y-intercept.
Solution:
Given that the equation is
5x + 6y + 12 = 0
6y = 5x + 12
y = 5/6x + 12/6.
y = 5/6x + 2
Comparing the equation with y = mx + c,
we have m = 5/6 and c = 2
Therefore, the slope of the line is 5/6. y-intercept is c = 2
Example 4.
What is the slope of the equation 2x – 4y + 10 = 0?
Solution:
Given that the equation is
2x – 4y + 10 = 0
4y = 2x + 10
y = 2/4x + 10/4.
y = 1/2x + 5/2
Comparing the equation with y = mx + c,
we have m = 1/2.
Therefore, the slope of the line is 1/2.
Example 5.
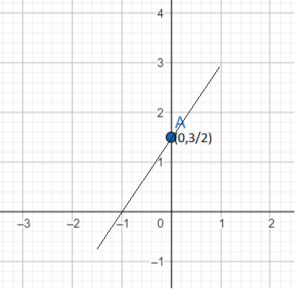
What is the slope and y-intercept of the line 3x – 6y + 12 = 0?
Solution:
Given that the equation is
3x – 8y + 12 = 0
8y = 3x + 12
y = 3/8x + 12/8.
y = 3/8x + 3/2
Comparing the equation with y = mx + c,
we have m = 3/8 and c = 3/2
Therefore, the slope of the line is ⅜ and y intercept c = 3/2
FAQs on Slope of the graph y = mx + c
1. What is the equation of a straight line?
The equation of the straight line is y = mx +c
where,
m is the slope and c is the y-intercept.
2. How do I find the slope in a graph?
Take two points on the line and determine their coordinates. Determine the difference in y-coordinates of these two points. Find the difference in x-coordinates for these two points. Divide the difference in y-coordinates by the difference in x-coordinates.
3. What is mx in the slope formula?
In the equation of a straight line y = mx + c, the slope is m which is multiplied by x and c is the y-intercept.