Practice with the help of Spectrum Math Grade 5 Answer Key Chapter 3 Posttest regularly and improve your accuracy in solving questions.
Spectrum Math Grade 5 Chapter 3 Posttest Answers Key
Add or subtract.
Question 1.
a.
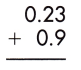
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
We can see that the given decimals are unlike, so we will convert them to like decimals by adding the required number of zeros. We will count the number of digits after the decimal point in both numbers and identify the higher one in them. In this case, 0.9 has one digit after the decimal, and 0.23 has two digits after the decimal. So, will make it 0.90 so that it becomes the same length as 0.23. Now, we will add the decimals numbers.
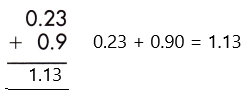
Therefore, the sum of the given decimals is 1.13
b.
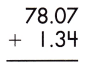
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
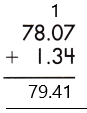
Therefore, the sum of the given decimals is 79.41
c.
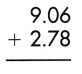
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
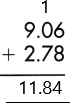
Therefore, the sum of the given decimals is 11.84
d.
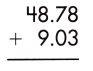
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
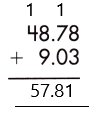
Therefore, the sum of the given decimals is 57.81
Question 2.
a.

Answer:
There are certain rules and steps which should be remembered while subtracting decimals.
– Change the given decimal fractions to like decimals.
– Write the smaller number below the greater number in such a way that the digits are placed in the corresponding places and the decimal points are placed in the same vertical line.
– Then, subtract the numbers in the same way as in the case of whole numbers.
– After the subtraction, place the decimal point in line with the other decimal points.
– Subtracting decimals with the same number of decimal places is simple. We just need to do the simple process of subtraction and then place the decimal points according to the given numbers.
– We can see that the numbers have the same decimal places. So, we will subtract them in a regular way.
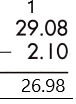
Therefore, the difference is 26.98
b.
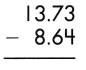
Answer:
There are certain rules and steps which should be remembered while subtracting decimals.
– Change the given decimal fractions to like decimals.
– Write the smaller number below the greater number in such a way that the digits are placed in the corresponding places and the decimal points are placed in the same vertical line.
– Then, subtract the numbers in the same way as in the case of whole numbers.
– After the subtraction, place the decimal point in line with the other decimal points.
– Subtracting decimals with the same number of decimal places is simple. We just need to do the simple process of subtraction and then place the decimal points according to the given numbers.
– We can see that the numbers have the same decimal places. So, we will subtract them in a regular way.
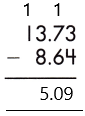
Therefore, the difference is 5.09
c.
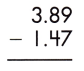
Answer:
There are certain rules and steps which should be remembered while subtracting decimals.
– Change the given decimal fractions to like decimals.
– Write the smaller number below the greater number in such a way that the digits are placed in the corresponding places and the decimal points are placed in the same vertical line.
– Then, subtract the numbers in the same way as in the case of whole numbers.
– After the subtraction, place the decimal point in line with the other decimal points.
– Subtracting decimals with the same number of decimal places is simple. We just need to do the simple process of subtraction and then place the decimal points according to the given numbers.
– We can see that the numbers have the same decimal places. So, we will subtract them in a regular way.
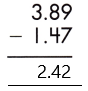
Therefore, the difference is 2.42
d.
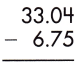
Answer:
There are certain rules and steps which should be remembered while subtracting decimals.
– Change the given decimal fractions to like decimals.
– Write the smaller number below the greater number in such a way that the digits are placed in the corresponding places and the decimal points are placed in the same vertical line.
– Then, subtract the numbers in the same way as in the case of whole numbers.
– After the subtraction, place the decimal point in line with the other decimal points.
– Subtracting decimals with the same number of decimal places is simple. We just need to do the simple process of subtraction and then place the decimal points according to the given numbers.
– We can see that the numbers have the same decimal places. So, we will subtract them in a regular way.
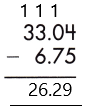
Therefore, the difference is 26.29
Question 3.
a.
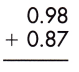
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
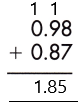
Therefore, the sum of the given decimals is 1.85
b.
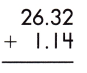
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
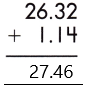
Therefore, the sum of the given decimals is 27.46
c.
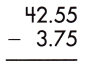
Answer:
There are certain rules and steps which should be remembered while subtracting decimals.
– Change the given decimal fractions to like decimals.
– Write the smaller number below the greater number in such a way that the digits are placed in the corresponding places and the decimal points are placed in the same vertical line.
– Then, subtract the numbers in the same way as in the case of whole numbers.
– After the subtraction, place the decimal point in line with the other decimal points.
– Subtracting decimals with the same number of decimal places is simple. We just need to do the simple process of subtraction and then place the decimal points according to the given numbers.
– We can see that the numbers have the same decimal places. So, we will subtract them in a regular way.

Therefore, the difference is 38.80
d.
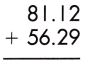
Answer:
While adding decimals, we need to remember some rules that would be helpful and make the addition easier.
– Align the decimal numbers in such a way that they are placed in the correct place according to their place values.
– Always convert the decimal numbers to like decimals, wherever needed.
– Add zeros in the places wherever the length of the decimal numbers is not the same.
– Now, add the numbers and place the decimal point aligned with the given decimal points.
– If we observe the given decimals, we see that they are like decimals, so, we will place them in order and do the regular addition.
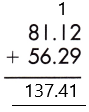
Therefore, the sum of the given decimals is 137.41
Multiply or divide.
Question 4.
a.
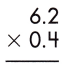
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
62 x 4 = 248
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 6.2 = 1
And the number of decimal places in 0.4 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 1 + 1 = 2
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 2, the resultant product must contain the decimal point after 2 digits from the rightmost place.
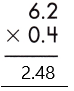
– Therefore, the product of the given decimals is 2.48
b.

Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
305 x 283 = 86315

2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 3.05 = 2
And the number of decimal places in 2.83 = 2
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 2 = 4
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 4, the resultant product must contain the decimal point after 4 digits from the rightmost place.
– Therefore, the product of the given decimals is 8.6315
c.
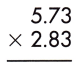
Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.

2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 5.73 = 2
And the number of decimal places in 2.83 = 2
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 2 + 2 = 4
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 4, the resultant product must contain the decimal point after 4 digits from the rightmost place.
– Therefore, the product of the given decimals is 16.2159
d.

Answer:
Multiplication of a decimal number by another decimal can be performed similarly to the multiplication of whole numbers except keeping the decimal point in the result. The below figure shows the process of multiplying decimal numbers by another decimal number.
steps:
1. Multiply both decimal numbers as whole numbers by removing the decimal point.
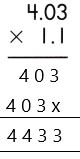
2. Count the number of digits to the right of the decimal point in both decimal numbers.
Thus, the number of digits after the decimal point in 4.03 = 2
And the number of decimal places in 1.1 = 1
3. Add the number of digits counted for the decimal point.
Total number of decimal places = 1 + 2 = 3
4. Put the decimal point in the product by counting the same digits as obtained in the previous step from its rightmost place.
– As the total number of decimal places is 3, the resultant product must contain the decimal point after 3 digits from the rightmost place.
– Therefore, the product of the given decimals is 4.433
Question 5.
a.
![]()
Answer:
There will be certain rules for dividing decimals in maths. These can be observed from the illustrative examples below.
Step 1: Write the given division expression in the standard form.
Step 2: Now, we have to divide the decimal number’s whole number part by the divisor.
Step 3: Place the decimal point in the quotient above the dividend’s decimal point and then bring down the tenth digit.
Step 4: If the tenth digit of the obtained dividend cannot be divided by the divisor, write 0 in the quotient and in front of the tenth digit. Otherwise, proceed with the division process.
Step 5: Repeat the above step and keep adding the zeroes in the dividend until 0 is obtained in the remainder.
Change the divisor 0.25 to a whole number by moving the decimal point 2 places to the right. Then move the decimal point in the dividend the same, 2 places to the right.
We then have the equations:
6500 ÷ 25 = 260.00
and therefore:
65 ÷ 0.25 = 260.00
Both were calculated to 2 decimal places.
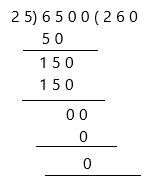
Therefore, the remainder is 0 and the quotient is 260.
b.
![]()
Answer:
There will be certain rules for dividing decimals in maths. These can be observed from the illustrative examples below.
Step 1: Write the given division expression in the standard form.
Step 2: Now, we have to divide the decimal number’s whole number part by the divisor.
Step 3: Place the decimal point in the quotient above the dividend’s decimal point and then bring down the tenth digit.
Step 4: If the tenth digit of the obtained dividend cannot be divided by the divisor, write 0 in the quotient and in front of the tenth digit. Otherwise, proceed with the division process.
Step 5: Repeat the above step and keep adding the zeroes in the dividend until 0 is obtained in the remainder.
Change the divisor 0.04 to a whole number by moving the decimal point 2 places to the right. Then move the decimal point in the dividend the same, 2 places to the right.
We then have the equations:
1900 ÷ 4 = 475.00
and therefore:
19 ÷ 0.04 = 475.00
Both were calculated to 2 decimal places.
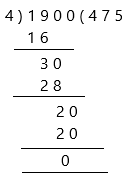
Therefore, the remainder is 0 and the quotient is 475
c.
![]()
Answer:
When we divide decimals, we have to convert the divisor to a whole number by moving the decimal point to the right. Then, we carry the dividend’s decimal point up to the same number of places to the right and divide the resultant numbers in the usual way as we perform in regular long division.
Change the divisor 0.7 to a whole number by moving the decimal point 1 place to the right. Then move the decimal point in the dividend the same, 1 place to the right.
We then have the equations:
132.3 ÷ 7 = 18.90
and therefore:
13.23 ÷ 0.7 = 18.90
Both were calculated to 2 decimal places.
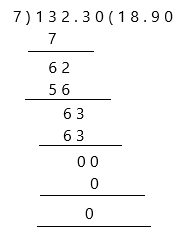
Therefore, the remainder is 0 and the quotient is 18.9
d.
![]()
Answer:
When we divide decimals, we have to convert the divisor to a whole number by moving the decimal point to the right. Then, we carry the dividend’s decimal point up to the same number of places to the right and divide the resultant numbers in the usual way as we perform in regular long division.
Change the divisor 1.3 to a whole number by moving the decimal point 1 place to the right. Then move the decimal point in the dividend the same, 1 place to the right.
We then have the equations:
28.6 ÷ 13 = 2.20
and therefore:
2.86 ÷ 1.3 = 2.20
Both were calculated to 2 decimal places
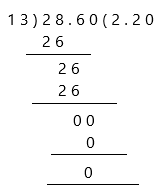
Therefore, the remainder is 0 and the quotient is 2.20
Solve each problem.
Question 6.
Sheila bought three books for $12.63, $9.05, and $ 14.97. How much did she spend?
Sheila spent __________ on the three books.
Answer:
The above-given:
The number Sheila bought = 3
The cost of book 1 = $12.63
The cost of book 2 = $9.05
The cost of book 3 = $14.97
The amount she spends on the three books = b
Based on the given conditions, we can formulate:
b = 12.63 + 9.05 + 14.97
b = 36.65
Therefore, she spent $36.65 on the three books.
Question 7.
Roberto bought a 12-pack of bottled water. Each bottle held 0.75 liters. How many liters of water did he buy?
Roberto bought _______________ liters.
Answer:
The above-given:
The number of bottles Roberto bought = 12
The number of litres each bottle held = 0.75
The number of litres he buys = x
Based on the given conditions, we can formulate;
x = 12 x 0.75
x = 9
Therefore, he bought 9 litres.
Question 8.
The highest batting average on the Owls baseball team is 0.42. The lowest batting average is 0.18. What is the difference?
The difference is ____.
Answer:
The above-given:
The highest average of the Owls baseball team is 0.42
The lowest average = 0.18
The difference = t
t = 0.42 – 0.18
t = 0.24
Therefore, the difference is 0.24
Question 9.
Lou spent $17.65 to buy 5 items of equal value. How much did he spend on each item?
Lou spent ________________ on each item.
Answer:
The above-given:
The number of items = 5
The total amount she spent = $17.65
The amount she spent on each item = x
Based on the given conditions, we can formulate:
x = 17.65/5
x = 3.53
Therefore, she spent $3.53 on each item.
Question 10.
A hike is 26.4 miles. Alicia wants to divide it equally over 3 days. How far does she need to hike each day?
She needs to hike __________________ miles each day.
Answer:
The above-given:
The total number of miles = 26.4
The number of days = 3
The number of miles she needs to walk each day = h
Based on the given conditions, we can formulate:
h = 26.4/3
h = 8.8
Therefore, she needs to walk 8.8 miles each day.
Question 11.
There are 6.75 buckets of sand in a sandbox. If each full bucket holds 4.32 pounds of sand, how many pounds of sand are there in the sandbox?
There are _____________ pounds of sand in the sandbox.
Answer:
The above-given:
The number of buckets of sand in the sandbox = 6.75
The number of pounds of sand each bucket holds = 4.32
The remaining sand in the sandbox = s
s = 6.75 – 4.32
s = 2.43
Therefore, 2.43 pounds of sand are in the sandbox.