Go through the Spectrum Math Grade 6 Answer Key Chapter 2 Lesson 2.2 Using Visual Models to Divide Fractions and get the proper assistance needed during your homework.
Spectrum Math Grade 6 Chapter 2 Lesson 2.2 Using Visual Models to Divide Fractions Answers Key
Fraction bars can be used to help divide fractions.

When dividing \(\frac{1}{3}\) by \(\frac{1}{6}\), you are finding out how many sixths are equal to \(\frac{1}{3}\).
When you line up the fraction bars and divide them into the appropriate pieces, you can see that \(\frac{2}{6}\) is equal to \(\frac{1}{3}\).
Therefore,
\(\frac{1}{3}\) ÷ \(\frac{1}{6}\) = 2
Use the fraction bars to solve the problems. Write answers in simplest form.
Question 1.
\(\frac{1}{2}\) ÷ \(\frac{1}{4}\) = _____

Answer:
Simplest form of \(\frac{1}{2}\) ÷ \(\frac{1}{4}\) is 2.
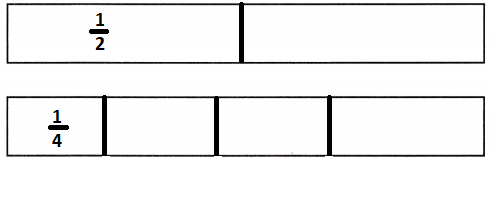
Explanation:
\(\frac{1}{2}\) ÷ \(\frac{1}{4}\)
= \(\frac{1}{2}\) × \(\frac{4}{1}\)
= \(\frac{1}{1}\) × \(\frac{2}{1}\)
= \(\frac{2}{1}\)
= 2.
Question 2.
\(\frac{2}{3}\) ÷ \(\frac{1}{6}\) = _____

Answer:
Simplest form of \(\frac{2}{3}\) ÷ \(\frac{1}{6}\) is 4.
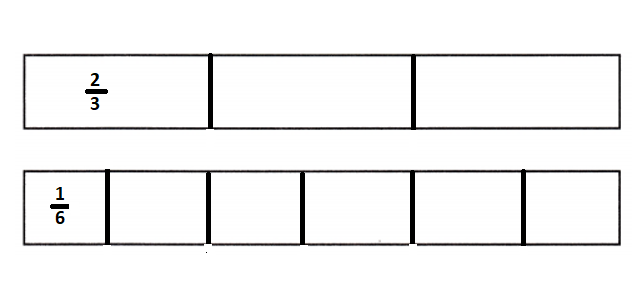
Explanation:
\(\frac{2}{3}\) ÷ \(\frac{1}{6}\)
= \(\frac{2}{3}\) × \(\frac{6}{1}\)
= \(\frac{2}{1}\) × \(\frac{2}{1}\)
= \(\frac{4}{1}\)
= 4.
Question 3.
\(\frac{3}{5}\) ÷ \(\frac{1}{15}\) = _____

Answer:
Simplest form of \(\frac{3}{5}\) ÷ \(\frac{1}{15}\) is 9.
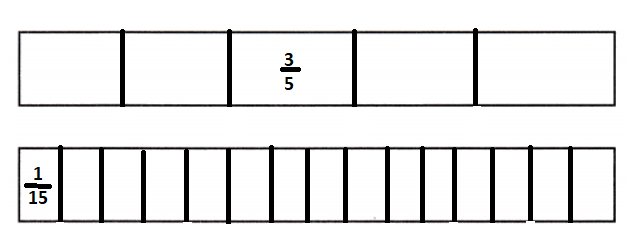
Explanation:
\(\frac{3}{5}\) ÷ \(\frac{1}{15}\)
= \(\frac{3}{5}\) × \(\frac{15}{1}\)
= \(\frac{3}{1}\) × \(\frac{3}{1}\)
= \(\frac{9}{1}\)
= 9.
Use the fraction bars to solve the problems. Write answers in simplest form.
Question 1.
\(\frac{1}{8}\) ÷ \(\frac{1}{2}\) = _____

Answer:
Simplest form of \(\frac{1}{8}\) ÷ \(\frac{1}{2}\) is \(\frac{1}{4}\).
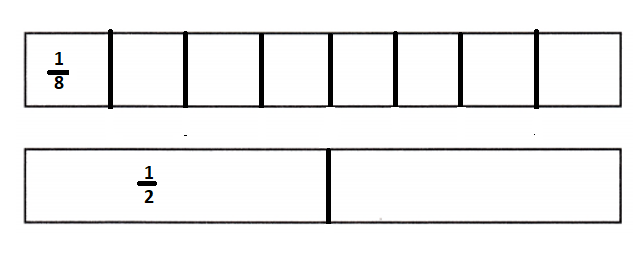
Explanation:
\(\frac{1}{8}\) ÷ \(\frac{1}{2}\)
= \(\frac{1}{8}\) × \(\frac{2}{1}\)
= \(\frac{1}{4}\) × \(\frac{1}{1}\)
= \(\frac{1}{4}\)
Question 2.
\(\frac{1}{10}\) ÷ \(\frac{2}{5}\) = _____

Answer:
Simplest form of \(\frac{1}{10}\) ÷ \(\frac{2}{5}\) is \(\frac{1}{4}\).
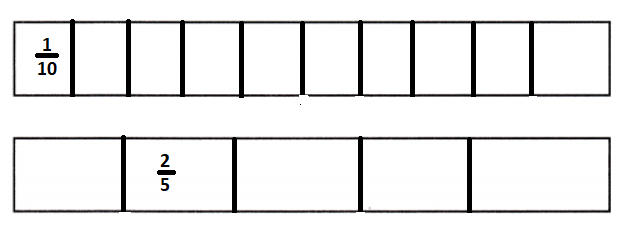
Explanation:
\(\frac{1}{10}\) ÷ \(\frac{2}{5}\)
= \(\frac{1}{10}\) × \(\frac{5}{2}\)
= \(\frac{1}{2}\) × \(\frac{1}{2}\)
= \(\frac{1}{4}\)
Question 3.
\(\frac{1}{12}\) ÷ \(\frac{1}{4}\) = _____

Answer:
Simplest form of \(\frac{1}{12}\) ÷ \(\frac{1}{4}\) is \(\frac{1}{3}\).
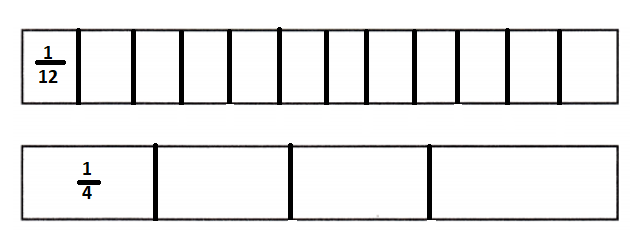
Explanation:
\(\frac{1}{12}\) ÷ \(\frac{1}{4}\)
= \(\frac{1}{12}\) × \(\frac{4}{1}\)
= \(\frac{1}{3}\) × \(\frac{1}{1}\)
= \(\frac{1}{3}\)
Question 4.
\(\frac{2}{9}\) ÷ \(\frac{1}{3}\) = _____

Answer:
Simplest form of \(\frac{2}{9}\) ÷ \(\frac{1}{3}\) is \(\frac{2}{3}\).
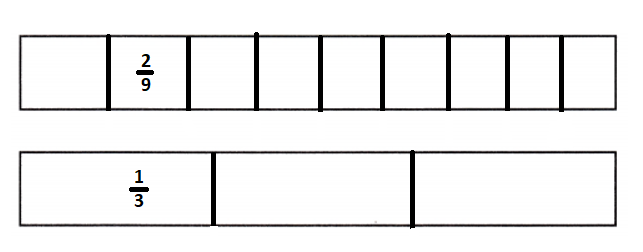
Explanation:
\(\frac{2}{9}\) ÷ \(\frac{1}{3}\)
= \(\frac{2}{9}\) × \(\frac{3}{1}\)
= \(\frac{2}{3}\) × \(\frac{1}{1}\)
= \(\frac{2}{3}\)