This handy Spectrum Math Grade 7 Answer Key Chapter 2 Pretest provides detailed answers for the workbook questions
Spectrum Math Grade 7 Chapter 2 Pretest Answers Key
Multiplying and Dividing Rational Numbers
Rewrite each expression using the distributive property.
Question 1.
a.
(x × 3) + (x × 7) =
___________
Answer: x × ( 3 + 7)
(x × 3) + (x × 7) = x × ( 3 + 7)
The distributive property states that multiplying the sum of two or more addends by a number yields the same outcome as multiplying each addend separately by the number and combining the resulting products.
b.
8 × (b + 12) =
___________
Answer: (8 × b) + (8 × 12)
8 × (b + 12) = (8 × b) + (8 × 12)
The distributive property states that multiplying the sum of two or more addends by a number yields the same outcome as multiplying each addend separately by the number and combining the resulting products.
Question 2.
a.
4 × (3 + c) =
___________
Answer: (4 × 3) + (4 × c)
4 × (3 + c) = (4 × 3) + (4 × c)
The distributive property states that multiplying the sum of two or more addends by a number yields the same outcome as multiplying each addend separately by the number and combining the resulting products.
b.
(5 × m) + (5 × n) =
___________
Answer: 5 × (m + n)
(5 × m) + (5 × n) = 5 × (m + n)
The distributive property states that multiplying the sum of two or more addends by a number yields the same outcome as multiplying each addend separately by the number and combining the resulting products.
Identify the property described as commutative, associative, identity, or zero.
Question 3.
The product of any number and one is that number. _____________
Answer: Identity Property
The product of any number and one is that number is called Identity Property.
According to the identity property of multiplication, if a number is multiplied by 1 (one), the result will be the original number. This property is applied when numbers are multiplied by 1. If there is a number, x then the identity property implies that x × 1 = x.
Question 4.
When two numbers are multiplied together, the product is the same regardless of the order of the factors.
_____________
Answer: Commutative Property
When two numbers are multiplied together, the product is the same regardless of the order of the factors is called Commutative Property.
According to the commutative property of multiplication, changing the order of the numbers we are multiplying does not change the product. If there are two numbers, x and y, the commutative property of multiplication implies that x × y = y × x.
Question 5.
When a factor is multiplied by zero, the product is always 0. ___________
Answer: Zero Property
According to the zero property of multiplication, if a number is multiplied by 0 (zero), the result will be zero. This property is applied when numbers are multiplied by 0. If there is a number, x then the identity property implies that x × 0 = 0.
Question 6.
When three or more numbers are multiplied together, the product is the same regardless of how the factors are grouped. _____
Answer: associative property
When three or more numbers are multiplied together, the product is the same regardless of how the factors are grouped is called associative property.
According to the associative principle of multiplication, when multiplying three integers, the outcome will always be the same regardless of how the numbers are grouped. If there are three numbers, x, y and z, the associative property of multiplication implies that x × (y × z) = (x × y) × z.
Question 7.
a. 6 × 0 = 0
___________
Answer: Zero Property
6 × 0 = 0
The above expression is the example for zero property.
According to the zero property of multiplication, if a number is multiplied by 0 (zero), the result will be zero. This property is applied when numbers are multiplied by 0. If there is a number, x then the identity property implies that x × 0 = 0.
b. (5 × 4) × 6 = 5 × (4 × 6)
___________
Answer: associative property
5 × 4) × 6 = 5 × (4 × 6)
The above expression is the example for associative property.
According to the associative principle of multiplication, when multiplying three integers, the outcome will always be the same regardless of how the numbers are grouped. If there are three numbers, x, y and z, the associative property of multiplication implies that x × (y × z) = (x × y) × z.
Question 8.
a. a × 1 = a
___________
Answer: Identity Property
a × 1 = a
The above expression is the example for Identity Property.
According to the identity property of multiplication, if a number is multiplied by 1 (one), the result will be the original number. This property is applied when numbers are multiplied by 1. If there is a number, x then the identity property implies that x × 1 = x.
b. 8 × 9 = 9 × 8
___________
Answer: Commutative Property
8 × 9 = 9 × 8
The above expression is the example for Commutative Property.
When two numbers are multiplied together, the product is the same regardless of the order of the factors is called Commutative Property.
According to the commutative property of multiplication, changing the order of the numbers we are multiplying does not change the product. If there are two numbers, x and y, the commutative property of multiplication implies that x × y = y × x.
Change each rational number into a decimal using long division.
Question 9.
a. \(\frac{3}{5}\) = ___________
Answer: 0.6

Rational numbers can be converted into decimals using long division. All fractions will be turned into decimals that either terminate or repeat. Repeating decimals can be given as a same pattern of numbers will get when we perform division. A line will be placed above the digits which are repeating.
Here, If we divide 3 by 5, we will get terminating decimal 0.6
Therefore, \(\frac{3}{5}\) = 0.6
b. \(\frac{4}{8}\) = ___________
Answer: 0.5
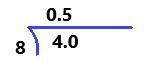
Rational numbers can be converted into decimals using long division. All fractions will be turned into decimals that either terminate or repeat. Repeating decimals can be given as a same pattern of numbers will get when we perform division. A line will be placed above the digits which are repeating.
Here, If we divide 4 by 8, we will get terminating decimal 0.5
Therefore, \(\frac{4}{8}\) = 0.5
Question 10.
a. \(\frac{1}{4}\) = ___________
Answer: 0.25

Rational numbers can be converted into decimals using long division. All fractions will be turned into decimals that either terminate or repeat. Repeating decimals can be given as a same pattern of numbers will get when we perform division. A line will be placed above the digits which are repeating.
Here, If we divide 1 by 4, we will get terminating decimal 0.25
Therefore, \(\frac{1}{4}\) = 0.25
b. \(\frac{7}{10}\) = ___________
Answer: 0.7

Rational numbers can be converted into decimals using long division. All fractions will be turned into decimals that either terminate or repeat. Repeating decimals can be given as a same pattern of numbers will get when we perform division. A line will be placed above the digits which are repeating.
Here, If we divide 7 by 10, we will get terminating decimal 0.7
Therefore, \(\frac{7}{10}\) = 0.7
Multiply or divide. Write answers in simplest form.
Question 11.
a. \(\frac{3}{8}\) × \(\frac{4}{5}\) = ______
Answer: \(\frac{3}{10}\)
\(\frac{3}{8}\) × \(\frac{4}{5}\)
Reduce the above fractions into simplest form if possible.
Then, multiply the numerators and denominators separately.
= \(\frac{3 × 4}{8 × 5}\)
Divide 4 in numerator and 8 in denominator with 4, which is the common factor
= \(\frac{3 × 1}{2 × 5}\)
= \(\frac{3}{10}\)
Therefore, \(\frac{3}{8}\) × \(\frac{4}{5}\) = \(\frac{3}{10}\)
b. \(\frac{1}{2}\) × \(\frac{3}{7}\) = ______
Answer: \(\frac{3}{14}\)
\(\frac{1}{2}\) × \(\frac{3}{7}\)
Reduce the above fractions into simplest form if possible.
Then, multiply the numerators and denominators separately.
= \(\frac{1 × 3}{2 × 7}\)
= \(\frac{3}{14}\)
Therefore, \(\frac{1}{2}\) × \(\frac{3}{7}\) = \(\frac{3}{14}\)
c. 2\(\frac{3}{4}\) × 1\(\frac{2}{7}\) = ______
Answer: 3\(\frac{15}{28}\)
2\(\frac{3}{4}\) × 1\(\frac{2}{7}\)
Convert the above numbers into improper fractions to make the calculations easy.
= \(\frac{11}{4}\) × \(\frac{9}{7}\)
Reduce the above fractions into simplest form if possible.
Then, multiply the numerators and denominators separately.
= \(\frac{11 × 9}{4 × 7}\)
= \(\frac{99}{28}\)
= 3\(\frac{15}{28}\)
Therefore, 2\(\frac{3}{4}\) × 1\(\frac{2}{7}\) = 3\(\frac{15}{28}\)
Question 12.
a. 6\(\frac{1}{8}\) ÷ 2\(\frac{4}{7}\) = ______
Answer: 2\(\frac{55}{144}\)
6\(\frac{1}{8}\) ÷ 2\(\frac{4}{7}\)
Convert the above numbers into improper fractions to make the calculations easy.
= \(\frac{49}{8}\) ÷ \(\frac{18}{7}\)
To divide by a fraction, multiply by its reciprocal.
Here, the reciprocal of \(\frac{18}{7}\) = \(\frac{7}{18}\)
So, \(\frac{49}{8}\) ÷ \(\frac{18}{7}\) = \(\frac{49}{8}\) × \(\frac{7}{18}\)
Reduce the above fractions into simplest form if possible.
Then, multiply the numerators and denominators separately.
= \(\frac{49 × 7}{8 × 18}\)
= \(\frac{343}{144}\)
= 2\(\frac{55}{144}\)
Therefore, 6\(\frac{1}{8}\) ÷ 2\(\frac{4}{7}\) = 2\(\frac{55}{144}\)
b. 3\(\frac{2}{3}\) ÷ 8 = ______
Answer: \(\frac{11}{24}\)
3\(\frac{2}{3}\) ÷ 8
Convert the above numbers into improper fractions to make the calculations easy.
= \(\frac{11}{3}\) ÷ \(\frac{8}{1}\)
To divide by a fraction, multiply by its reciprocal.
Here, the reciprocal of \(\frac{8}{1}\) = \(\frac{1}{8}\)
So, \(\frac{11}{3}\) ÷ \(\frac{8}{1}\) = \(\frac{11}{3}\) × \(\frac{1}{8}\)
Reduce the above fractions into simplest form if possible.
Then, multiply the numerators and denominators separately.
= \(\frac{11 × 1}{3 × 8}\)
= \(\frac{11}{24}\)
Therefore, 3\(\frac{2}{3}\) ÷ 8 = \(\frac{11}{24}\)
c. 5\(\frac{1}{2}\) ÷ 1\(\frac{2}{5}\) = ______
Answer: 3\(\frac{13}{14}\)
5\(\frac{1}{2}\) ÷ 1\(\frac{2}{5}\)
Convert the above numbers into improper fractions to make the calculations easy.
\(\frac{11}{2}\) ÷ \(\frac{7}{5}\)
To divide by a fraction, multiply by its reciprocal.
Here, the reciprocal of \(\frac{7}{5}\) = \(\frac{5}{7}\)
\(\frac{11}{2}\) ÷ \(\frac{7}{5}\) = \(\frac{11}{2}\) × \(\frac{5}{7}\)
Reduce the above fractions into simplest form if possible.
Then, multiply the numerators and denominators separately.
= \(\frac{11 × 5}{2 × 7}\)
= \(\frac{55}{14}\)
= 3\(\frac{13}{14}\)
Question 13.
a. -3 × 4 = ______
Answer: -12
-3 × 4 = -12
The product of two positive integers is always positive.
The product of two negative integers is always positive.
The product of one positive and one negative integer is always negative.
Here -3 is a negative integer and 4 is a positive integer therefore the result of their product is a negative integer.
b. 6 × (-3) = ______
Answer: -18
The product of two positive integers is always positive.
The product of two negative integers is always positive.
The product of one positive and one negative integer is always negative.
Here -3 is a negative integer and 6 is a positive integer therefore the result of their product is a negative integer.
c. -2 × (-8) = ______
Answer: 16
The product of two positive integers is always positive.
The product of two negative integers is always positive.
The product of one positive and one negative integer is always negative.
Here -2 and -8 both are negative integers hence their product is also a negative integer.
Question 14.
a. -18 ÷ 9 = ______
Answer: -2
let -18 ÷ 9 = x
As division and multiplication are inverse operations, the above equation can be written as follows
-18 = x × 9
x = -2
-18 ÷ 9 = -2
Therefore Inverse operation: -2
The quotient of two integers with the same sign is positive and the quotient of two integers with different signs is negative. Here -18 and 9 both are having different sign hence the result would be negative.
b. 24 ÷ (-6) = ______
Answer: -4
let 24 ÷ (-6) = x
As division and multiplication are inverse operations, the above equation can be written as follows
24 = x × (-6)
x = -4
24 ÷ (-6) = -4
Therefore Inverse operation: -4
The quotient of two integers with the same sign is positive and the quotient of two integers with different signs is negative. Here 24 and -6 both are having different sign hence the result would be negative.
c. -40 ÷ (-4) = ______
Answer: 10
let -40 ÷ (-4) = x
As division and multiplication are inverse operations, the above equation can be written as follows
-40 = x × (-4)
x = 10
-40 ÷ (-4) = 10
Therefore Inverse operation: 10
The quotient of two integers with the same sign is positive and the quotient of two integers with different signs is negative. Here -40 and -4 both are having same sign hence the result would be positive.
Solve each problem.
Question 15.
A ribbon that is 22\(\frac{3}{4}\) inches long must be cut into 7 equal pieces. How long will each piece be?
Each piece will be ____ inches long.
Answer: 3\(\frac{7}{28}\)
A ribbon that is 22\(\frac{3}{4}\) inches long must be cut into 7 equal pieces.
22\(\frac{3}{4}\) can be converted into improper fraction, which is \(\frac{91}{4}\)
The length of each piece = 22\(\frac{3}{4}\) ÷ 7
= \(\frac{91}{4}\) ÷ 7
To divide by a fraction, multiply by its reciprocal.
Here, the reciprocal of \(\frac{7}{1}\) = \(\frac{1}{7}\)
So, \(\frac{91}{4}\) × \(\frac{1}{7}\)
Reduce the above fractions into simplest form if possible.
Then, multiply the numerators and denominators separately.
= \(\frac{91 × 1}{4 × 7}\)
= \(\frac{91}{28}\)
= 3\(\frac{7}{28}\)
Therefore, Each piece will be 3\(\frac{7}{28}\) inches long.
Question 16.
Fifteen cups of flour are to be stored in containers. Each container holds 2\(\frac{1}{3}\) cups. How many containers will the flour fill? What fraction of another container will it fill?
The flour will fill _____ full containers and _____ of another container.
Answer: 6 and \(\frac{3}{7}\)
Fifteen cups of flour are to be stored in containers.
Each container holds 2\(\frac{1}{3}\) cups.
The amount of filled containers = 15 ÷ 2\(\frac{1}{3}\)
Change 2\(\frac{1}{3}\) into improper fraction, which is \(\frac{7}{3}\)
so, 15 ÷ \(\frac{7}{3}\)
To divide by a fraction, multiply by its reciprocal.
Here, the reciprocal of \(\frac{7}{3}\) = \(\frac{3}{7}\)
So, \(\frac{15}{1}\) × \(\frac{3}{7}\)
Reduce the above fractions into simplest form if possible.
Then, multiply the numerators and denominators separately.
= \(\frac{15 × 3}{1 × 7}\)
= \(\frac{45}{7}\)
= 6\(\frac{3}{7}\)
Therefore, The flour will fill 6 full containers and \(\frac{3}{7}\) of another container.
Question 17.
There are 7\(\frac{1}{2}\) bottles of lemonade. Each bottle holds 1\(\frac{5}{6}\) quarts. How many quarts of lemonade are there?
There are ____ quarts of lemonade.
Answer: 9\(\frac{1}{6}\)
There are 7\(\frac{1}{2}\) bottles of lemonade. Each bottle holds 1\(\frac{5}{6}\) quarts.
The number of quarts of lemonade = 7\(\frac{1}{2}\) × 1\(\frac{5}{6}\)
Convert the above number into improper fractions to make the calculations easy.
So, 7\(\frac{1}{2}\) × 1\(\frac{5}{6}\) = \(\frac{15}{2}\) × \(\frac{11}{6}\)
Reduce the above fractions into simplest form if possible.
Then, multiply the numerators and denominators separately.
= \(\frac{15 × 11}{2 × 6}\)
Divide 15 in numerator and 6 in denominator by 3, which is a common factor
= \(\frac{5 × 11}{2 × 3}\)
= \(\frac{55}{6}\)
= 9\(\frac{1}{6}\)
Therefore, There are 9\(\frac{1}{6}\) quarts of lemonade.
Question 18.
If the length of the pool is 14\(\frac{1}{2}\) feet, the width is 6\(\frac{1}{2}\) feet, and the depth is 6\(\frac{1}{2}\) feet, what is the volume of the pool?
The volume of the pool is ____ cubic feet.
Answer: 612\(\frac{5}{8}\)
If the length of the pool is 14\(\frac{1}{2}\) feet, the width is 6\(\frac{1}{2}\) feet, and the depth is 6\(\frac{1}{2}\) feet
the volume of the pool is 14\(\frac{1}{2}\) × 6\(\frac{1}{2}\) × 6\(\frac{1}{2}\)
Convert the above number into improper fractions to make the calculations easy.
14\(\frac{1}{2}\) = \(\frac{29}{2}\)
6\(\frac{1}{2}\) = \(\frac{13}{2}\)
So, 14\(\frac{1}{2}\) × 6\(\frac{1}{2}\) × 6\(\frac{1}{2}\) = \(\frac{29}{2}\) × \(\frac{13}{2}\) × \(\frac{13}{2}\)
Reduce the above fractions into simplest form if possible.
Then, multiply the numerators and denominators separately.
= \(\frac{29 × 13 × 13}{2 × 2 × 2}\)
= \(\frac{4901}{8}\)
= 612\(\frac{5}{8}\)
Therefore, The volume of the pool is 612\(\frac{5}{8}\) cubic feet.