This handy Spectrum Math Grade 7 Answer Key Chapter 3 Lesson 3.5 Using Variables to Express Inequalities provides detailed answers for the workbook questions.
Spectrum Math Grade 7 Chapter 3 Lesson 3.5 Using Variables to Express Inequalities Answers Key
An inequality is a mathematical sentence that states that Iwo expressions are not equal.
2 × 5 > 6
Inequalities can be solved the same way as you solve equations.
-4 × x ≥ -4
-4 × x ÷ (-4) ≥ -4 ÷ (-4)
x ≤ 1
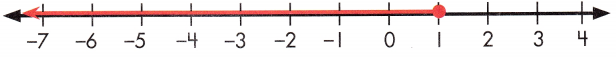
When you multiply or divide by a negative number, you must flip the inequality sign.
Solve each inequality and graph its solution.
Question 1.
a. -4 × m > 20

Answer:
An inequality is a mathematical sentence that states that Iwo expressions are not equal.
-4 × m > 20
-4 × m ÷ (-4) > 20 ÷ (-4)
m < -5
When you multiply or divide by a negative number, you must flip the inequality sign.

b. \(\frac{v}{5}\) ≤ –\(\frac{3}{5}\)

Answer:
An inequality is a mathematical sentence that states that Iwo expressions are not equal.
\(\frac{v}{5}\) ≤ –\(\frac{3}{5}\)
\(\frac{v}{5}\) × 5 ≤ –\(\frac{3}{5}\) × 5
v ≤ -3

Question 2.
a. 15 × x ≤ 15

Answer:
An inequality is a mathematical sentence that states that Iwo expressions are not equal.
15 × x ≤ 15
15 × x ÷15 ≤ 15÷15
x ≤ 1

b. h ÷ 6 < -12

Answer:
An inequality is a mathematical sentence that states that Iwo expressions are not equal.
h ÷ 6 < -12
h ÷ 6 × 6< -12 × 6
h < -72

Question 3.
a. -10a < -70

Answer:
An inequality is a mathematical sentence that states that Iwo expressions are not equal.
-10a < -70
-10a ÷ (-10) < -70 ÷ (-10)
a > 7
When you multiply or divide by a negative number, you must flip the inequality sign.

b. n ÷ 2 ≥ 2

Answer:
An inequality is a mathematical sentence that states that Iwo expressions are not equal.
n ÷ 2 ≥ 2
n ÷ 2 × 2 ≥ 2 ×2
n ≥ 4

Word problems can be solved by creating inequality statements.
Aria has $55 to spend on flowers. She wants to buy two rose bushes, which will cost $20, and spend the rest of her money on lilies. Each lily costs $ 10. Write an inequality to show how many lilies Aria can buy.
Let l represent the number of lilies she can buy.
Inequality: $ 10 × l + $20 ≤ $55
$10 × l + $20 – $20 ≤ $55 – $20
$10 × l ÷ $10 ≤ $35 ÷ $10
1 ≤ 3.5
Aria can buy 3 lilies.
Solve each problem by creating an inequality.
Question 1.
Andrew had $20 to spend at the fair. If he paid $5 to get into the fair, and rides cost $2 each, what is the maximum number of rides he could go on?

Let r represent the number of rides.
Inequality: $5 + r×$2 ≤ $20
Andrew could go on 7 rides.
Inequality: __________
Andrew could go on _____ rides.
Answer:
Andrew had $20 to spend at the fair.
he paid $5 to get into the fair, and rides cost $2 each.
Let r represent the number of rides.
Inequality: $5 + r×$2 ≤ $20
Add -$5 on both sides
-$5 + $5 + r×$2 ≤ $20 -$5
r×$2 ≤ $15
Divide $2 on both sides
r×$2 ÷$2≤ $15÷$2
r ≤ $7.5
Therefore, Andrew could go on 7 rides.
Question 2.
Sandra has $75 to spend on a new outfit. She finds a sweater that costs twice as much the skirt. What is the most the skirt can cost?
Let s represent the cost of the skirt.
Inequality: _________
The most the skirt can cost is __________
Answer:
Inequality: s + 2s ≤ $75
The most the skirt can cost is $25
Sandra has $75 to spend on a new outfit.
She finds a sweater that costs twice as much the skirt.
Let s represent the cost of the skirt.
Inequality: s + 2s ≤ $75
3s ≤ $75
divide 3 on both sides
3s ÷3≤ $75÷3
s ≤ $25
Therefore, The most the skirt can cost is $25
Question 3.
Alan earns $7.50 per hour at his after-school jobs. He is saving money to buy a skateboard that costs $ I 20. How many hours will he have to work to earn enough money for the skateboard?

Let h represent the number of hours Alan will have to work.
Inequality: _________
Alan will have to work _____ hours.
Answer:
Inequality: $7.50 × h ≤ $ 120
Alan will have to work 16 hours.
Alan earns $7.50 per hour at his after-school jobs.
He is saving money to buy a skateboard that costs $ 120.
Let h represent the number of hours Alan will have to work.
Inequality: $7.50 × h ≤ $ 120
Divide $7.50 by both sides
$7.50 × h ÷ $7.50 ≤ $ 120 ÷$7.50
h ≤ $16
Alan will have to work 16 hours.
Solve each problem by creating an inequality.
Question 1.
Blue Bird Taxi charges a $2.00 flat rate in addition to $0.55 per mile. Marcy only has $ 10 to spend on a taxi ride. What is the farthest she can ride without going over her limit?
Let d equal the distance Marcy can travel.
Inequality: ____________
Marcy can travel ____ miles without going over her limit.
Answer:
Inequality: 2.00 + 0.55 × d ≤ 10
Marcy can travel 14.54 miles without going over her limit.
Blue Bird Taxi charges a $2.00 flat rate in addition to $0.55 per mile.
Marcy only has $ 10 to spend on a taxi ride.
Let d equal the distance Marcy can travel.
Inequality: 2.00 + 0.55 × d ≤ 10
Add -2.00 on both sides
2.00 + 0.55 × d -2.00 ≤ 10 -2.00
0.55 × d≤ 8
divide by 0.55 on both sides
0.55 × d ÷0.55≤ 8÷0.55
d ≤ 14.54
Marcy can travel 14.54 miles without going over her limit.
Question 2.
The school store is selling notebooks for $ 1.50 and T-shirts for $ 10.00 to raise money for the school. They have a goal of raising $250 to buy supplies for the science lab. If they have sold 60 notebooks, how many T-shirts will they need to sell to reach their goal?
Let t equal the number of T-shirts.
Inequality: _______
They need to sell _____ T-shirts.
Answer:
Inequality: 60 × $ 1.50 + t × $ 10.00 ≤ $250
They need to sell 16 T-shirts.
The school store is selling notebooks for $ 1.50 and T-shirts for $ 10.00 to raise money for the school.
They have a goal of raising $250 to buy supplies for the science lab.
They have sold 60 notebooks
Let t equal the number of T-shirts.
Inequality: 60 × $ 1.50 + t × $ 10.00 ≤ $250
$90 + $10t ≤ $250
Add -$90 on both sides
$90 -$90 + $10t ≤ $250 – $90
$10t ≤ $160
Divide $10 on both sides
$10t ÷$10 ≤ $160÷$10
t ≤ $16
Therefore, they need to sell 16 T-shirts.
Question 3.
There are 178 7th grade students and 20 chaperones going on the field trip to the aquarium. Each bus holds 42 people. How many buses will the group have to take?

Let b represent the number of buses.
Inequality: ___________
They will need to take ____ buses.
Answer:
Inequality: b × 42 ≥ 198
They will need to take 5 buses.
There are 178 7th grade students and 20 chaperones going on the field trip to the aquarium.
Total number of people that can go to the trip = 178 + 20 = 198
Each bus holds 42 people.
Let b represent the number of buses.
Inequality: b × 42 ≥ 198
divide by 42 on both sides
42b ÷ 42≥198 ÷42
b ≥ 4.71
They will need to take 5 buses.
Question 4.
Sofia’s parents gave her an allowance for summer camp of $ 125. If she is going to be at camp for 6 weeks, what is the most she can spend each week while she is at camp?
Let m represent the amount Sofia can spend each week.
Inequality: __________
The most Sofia can spend each week is ______.
Answer:
Inequality: 6×m ≥$ 125
The most Sofia can spend each week is $20.833
Sofia’s parents gave her an allowance for summer camp of $ 125.
she is going to be at camp for 6 weeks
Let m represent the amount Sofia can spend each week.
Inequality: 6×m ≥$ 125
Divide 6 on both sides
6×m ÷6 ≥ $ 125 ÷6
m ≥ $20.833
The most Sofia can spend each week is $20.833
Question 5.
The cell phone company allows all users 450 text messages a month. Any text messages over the allowed amount are charged $0.25 per message. Craig only has $26 extra to spend on his cell phone bill. How many messages can he go over the allowed amount for the month without breaking his budget of $26?

Let p represent the amount of text messages Craig can go over.
Inequality: p × $0.25 ≤$26
Craig can send and receive 104 extra text messages without breaking his budget of $26.
Inequality: __________
Craig can send and receive ______ extra text messages without breaking his budget of $26.
Answer:
The cell phone company allows all users 450 text messages a month.
Any text messages over the allowed amount are charged $0.25 per message.
Craig only has $26 extra to spend on his cell phone bill.
Let p represent the amount of text messages Craig can go over.
Inequality: p × $0.25 ≤$26
divide by $0.25 on both sides
p × $0.25 ÷ $0.25≤ $26 ÷ $0.25
p ≤ 104
Therefore, Craig can use extra of 104 messages
In total, he can use 450 + 104 = 554 messages
