It is really easy to find Square root of numbers that are perfect squares when it comes to Square Root of Numbers that are Not Perfect Squares, it is difficult to find them. If you need to find the square root of a number m places of decimals, then the number of digits in the decimal part must be 2m. If the decimals are less than 2m, then add the required zeros at the right to the decimal part. Check out the complete concepts of Square Root on our website.
Square Root of Decimal Numbers using Long Division Method
Have a look at the procedure on how to solve square roots that aren’t perfect squares. They are as follows
- If we have to find a square root of number correct up to ‘n’ places of decimal, then we need to find the square root of number up to (n + 1) places of decimal.
- Also, if the digit place is (n + 1) decimal place is equal to 5 or greater than 5, then the digit at ‘n’ place increases by 1.
- Furthermore, if the digit place is (n + 1) decimal place is less than 5, then the digit at ‘n’ place remains the same and deletes the digit at (n + 1) place.
Square Root of Numbers that are not Perfect Squares Examples
1. Evaluate √2 correct up to two places of decimal?
Solution:
The given number is √2.
The square root of 1 is 1. Also, the square root of 2.25 is 1.5.
The 2 is in between 1 and 2.25.
Therefore, to find the square root of a 2, add 6 zeros after the decimal point.
√2.000000 = √(1.414 × 1.414)
Grouping the factors into the pairs of equal factors.
(1.414 × 1.414)
1.414 is the square root of 2.

The two places of decimal after the number is 1.41.
2. Evaluate √3 correct up to 3 places of decimal?
Solution:
The given number is √3.
The square root of 2.25 is 1.5. Also, the square root of 3.0625 is 1.75.
The 3 is in between 2.25 and 3.0625.
Therefore, to find the square root of a 3, add 10 zeros after the decimal point.
√3.0000000000 = √(1.7324 × 1.7324)
Grouping the factors into the pairs of equal factors.
(1.7324 × 1.7324)
1.7324 is the square root of 3.

The three places of decimal after the number is 1.732.
3. Evaluate √0.8 correct up to two places of decimal?
Solution:
The given number is √0.8.
The square root of 0.49 is 0.7. Also, the square root of 0.81 is 0.9.
The 0.8 is in between 0.7 and 0.9.
Therefore, to find the square root of 0.8, add 5zeros after the decimal point.
√0.800000 = √(0.894 × 0.894)
Grouping the factors into the pairs of equal factors.
(0.894 × 0.894)
0.894 is the square root of 0.8.
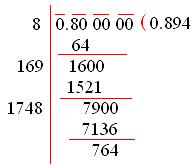
The two places of decimal after the number is 0.89.