Are you looking for all the theorems of inequalities in triangles? Then make use of our page and learn all the theorems. Now on this page, the students of 9th grade can find the theorem with proof of Sum of any two sides is greater than Twice the Median.
Sum of any Two Sides is Greater than Twice the Median
Theorem Statement:
Prove that sum of any two sides of a triangle is greater than twice the median?
Proof:
Given Triangle ABC in which AD is the median.
To prove: AB + AC > 2AD
Construction :
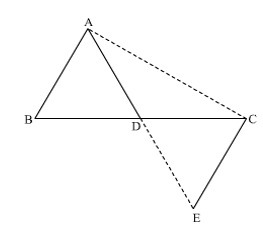
Extend AD to E such that AD = DE.
Now join EC.
Proof:
In ΔADB and ΔEDC
AD=DE[ By construction]
D is the midpoint BC.[DB=DB]
ΔADB=ΔEDC [vertically opposite angles]
Therefore Δ ADB ≅ ΔEDC [ By SAS congruence criterion.]
AB=ED[Corresponding parts of congruent triangles ]
In ΔAEC,
AC+ED> AE [sum of any two sides of a triangle is greater than the third side]
AC+AB>2AD[AE=AD+DE=AD+AD=2AD and ED=AB]
Hence proved.
Do Check:
FAQs on the sum of any two sides is Greater than Twice the Median
1. What is the relationship between the 2 parts of the median?
The centroid is always two-thirds of the way along each median from that median’s interior angle. This means that it sets up a 2:1 for each of the three medians: 2 parts of the median are between the centroid and the interior angle. 1 part of the median is between the centroid and the opposite side.
2. What is the relation between the median and sides of a triangle?
The relation between the median and the sides of a triangle is such that three times the sum of squares of the length of sides is equal to 4 times the squares of medians of a triangle.
3. What is the difference between median and altitude?
The difference between medians and altitudes is that a median is drawn from a vertex of the triangle to the midpoint of the opposite side, whereas an altitude is drawn from a vertex of the triangle to the opposite side being perpendicular to it.