In geometry, a triangle with all three sides of equal length is called an equilateral triangle. In the word equilateral, the word equi means equivalent and lateral means sides. Isosceles triangle theorem states that each angle of an equilateral triangle measures 60 degrees or a triangle is called equilateral if it is equiangular. The proof for the statement of equiangular is given here.
Prove that Three Angles of an Equilateral Triangle are Equal
The following is the proof for the statement three angles of an equilateral triangle are equal.
Given ABS is an equilateral triangle.
To prove: ∠ABC = ∠BAC = ∠ACB
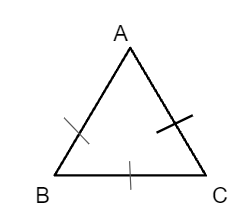
| Statement | Reason |
|---|---|
| ∠CAB = ∠ABC | Angles opposite to equal sides BC and AC are equal |
| ∠ABC = ∠ACB | Angles opposite to equal sides AC and AB are equal |
| ∠BAC = ∠ABC = ∠ACB | From the above two statements |
Hence proved.
Also, Check:
- An Altitude of an Equilateral Triangle is also a Median
- Point on the Bisector of an Angle
- Equal Sides of an Isosceles Triangle are Produced, the Exterior Angles are equal
- Geometry and Measurement
Note:
In an equilateral triangle ABC, let one angle be x°. Find the value of x°.
We know that the three angles of an equilateral triangle are equal.
So, ∠ABC = ∠BAC = ∠ACB = x°
The sum of 3 angles in a triangle si 180 degrees.
∠ABC + ∠BAC + ∠ACB = 180°
x° + x° + x° = 180°
3x° = 180°
x° = 180/3 = 60°
Therefore, each angle of an equilateral triangle is 60°.
Properties of an Equilateral Triangle
In an equilateral triangle, all three sides and angles are equal in measure. The value of each angle is 60 degrees, so it is called an equiangular triangle. Some of the properties of an equilateral triangle are provided here.
- The sides of an equilateral triangle are equal.
- It is a regular polygon with three sides.
- Angles are congruent and are equal to 60 degrees.
- The area of an equilateral triangle is √3side²/ 4 and the perimeter is 3side.
- The sum of all interior angles of an equilateral triangle is 180 degrees.
- Angle bisector, median and altitude of an equilateral triangle are the same.
- Ortho-center, the centroid is at the same point.
Questions on Equilateral Triangle
Question 1:
What is the area, perimeter of an equilateral triangle, if the side length is 5 cm?
Solution:
Given that,
Length of the side = 5 cm
Area of an equilateral triangle = √3side²/ 4
= √3 x 5²/ 4
= 25√3/4
The perimeter = 3side
= 3 x 5 = 15
Therefore, the area, the perimeter of an equilateral triangle are 25√3/4 sq cm, 15 cm.
Question 2:
How to find the other two angles of an isosceles triangle if one angle is x°.
Solution:
Let the isosceles triangle be XYZ.
As it is an isosceles triangle, XY = XZ
And ∠XYZ = ∠XZY = x°
Take the unknown angle as y° = ∠ZXY
The sum of interior angles of a triangle is 180 degrees
∠XYZ + ∠XZY + ∠ZXY = 180
x° + x° + y° = 180
y° = 180 – 2x°
x° = (y° – 180)/2
FAQ’s on All Angles of an Equilateral Triangle are Same
1. Do equilateral triangles have 3 equal angles?
Yes, an equilateral triangle has three equal sides and equal angles. Every angle in an equilateral triangle is always 60 degrees.
2. Why all angles are equal in an equilateral triangle?
As equilateral triangles have sides of equal length, therefore three angles opposite to equal sides are also equal.
3. Are equilateral triangles equal to 180?
Equilateral triangles have 3 equal angles. The sum of interior angles of a triangle is 180 degrees. So, each angle must be equal to 60 degrees.
4. When three angles of a triangle are equal then what it is called?
If three angles of a triangle are equal then it is said to be an equilateral triangle or equiangular triangle.