I think all the students of grade 9 are familiar with the solid figures. Here on this page, we will discuss in-depth the volume of cuboids like what the volume of cuboids exactly is, formulas, and how to calculate the volume of cuboids. Therefore the students who are looking forward to knowing about the volume of the cuboid can make use of our page and prepare well for the exams. In addition to this, you can find examples of the volume of the cuboid here.
What is the Volume of Cuboid?
Volume is the quantity that is used to measure solid figures like cuboids. A cuboid is a three-dimensional geometric figure. Simply we can say that a cuboid is a rectangular three-dimensional figure. In a rectangular cuboid, all the angles are right angles. A cuboid has 12 edges, 6 faces, and 8 vertices. A cuboid has three dimensions such as length, breadth, and height.

So, we can measure the space occupied by the cuboid by using the volume formula. The units of volume of a cuboid are cubic units. The volume of a cuboid completely depends upon the length, breadth, and height of the object.
Formula of Volume of Cuboid
The unit of volume of cuboids is cubic units like cu. meter, cu. cm, cu. inches etc.
The formula of volume of cuboid is l × b × h
where,
l = length
b = breadth
h = height
Volume of Cuboid Prism | Volume of Rectangular Prism
A cuboid or rectangular prism is the same. A cuboid has six faces, eight vertices, and 12 edges. We can say that a cuboid is a solid rectangle. The top and bottom surfaces are the same in the cuboid. We can find the volume of the cuboid prism using the formula.
The volume of a rectangular prism or cuboid prism = length × breadth × height
How to find Volume of Cuboid?
We know that the volume of the cuboid can be calculated using the dimensions of the given figure. So, to find the volume of the cuboid we have to follow some steps. The scenario to calculate the volume of the cuboid is shown below.
Step 1: Check the dimensions of the given cuboid.
Step 2: Check the length, breadth, and height and see whether all the units are the same.
Step 3: If the units are not the same then convert them and make them into the same units.
Step 4: And then apply the volume of the cuboid formula.
Step 5: At last write the obtained value and write it in cubic units.
Also, Check:
Volume of Cuboid Questions
Check out the problems given below to know how to find the volume of a cuboid. If you learn these problems the students of 9th grade can solve any type of problem from the topic Volume of Cuboid.
Example 1.
Find the volume of a cuboid of dimensions 2 cm × 4 cm × 6 cm.
Solution:
Given that
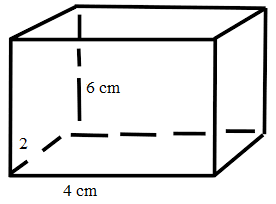
Length = 2 cm
Breadth = 4 cm
Height = 6 cm
We know that
The volume of cuboid = length × breadth × height.
Volume of cuboid = 2 cubic cm × 4 cubic cm × 6 cubic cm.
= 48 cubic cm.
Therefore, the volume of the cuboid = 48
Example 2.
A water tank is 10 cm long, 15 cm broad and 5 cm high. What is the volume of a water tank in cubic cm?
Solution:
Given that,
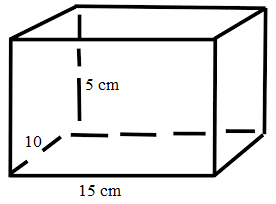
The length of the water tank = 10cm
The breadth of the water tank = 15 cm
The height of the water tank = 5 cm
We know that,
The volume of cuboid = length × breadth × height.
Volume of cuboid = 10 × 15 × 5 cuboid cm
Therefore, the volume of water tank = 750
Example 3.
Kiran made a bangle box for his sister with a length of 12 cm, breadth of 34 cm, and height of 18 cm. Find the volume of the bangle box.
Solution:
Given that,

Kiran made a bangle box for his sister of length = 12 cm
Kiran made a bangle box for his sister of breadth = 34 cm
Kiran made a bangle box for his sister of height = 18 cm
The volume of the bangle box = Length × breadth × height
= 12 × 34 × 18
= 7344cu cm.
Therefore, the volume of a bangle box = 7344 cu cm
Example 4.
Find the number of cubical boxes of 4 cm which can be accommodated in a carton of dimensions 24 cm × 6 cm × 8 cm.
Solution:
Given that,
Side of a box = 4
Volume of box = side × side × side.
= 4 × 4 × 4
= 64 cu. cm.
Volume of carton = length × breadth × height.

= 24 × 6 × 8
=1152 cu. cm.
A number of boxes = Volume of carton/Volume of each box.
= 1152/64
Therefore, the number of cubical boxes = 18.
Example 5.
How many bricks each 15 cm long, 3 cm wide, and 7cm thick will be required for a wall 2 m long, 22 m high, and 6 m thick? If bricks sell at $600 per thousand what will it cost to build the wall?
Solution:
Given that
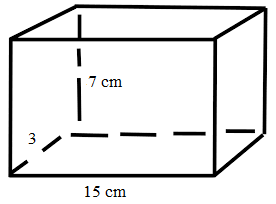
Length of the brick = 15 cm
Width of the brick = 3 cm
Thick of the brick = 7 cm
Volume of the wall = 15 m × 3 m × 7 m
= 2 × 100 cm × 22 × 100 cm × 6 × 100 cm
= 264000000
Volume of brick = 15 cm × 3 cm × 7 cm
= 315
Number of bricks = Volume of the wall/Volume of the brick
= 200 × 2200 × 600/15 × 3 × 7
= 264000000/315
The number of bricks = 838095
The cost of 1 thousand bricks = $ 600
The cost of building the wall = $ 600 × 838095 = $ 502857000
FAQs on Volume of Cuboid
1. How do we define the volume of a cuboid?
A volume of cuboids is defined as the amount of space occupied by the cuboid surface in a three-dimensional figure.
2. If the units of dimensions of a cuboid are different, then how to find the volume?
If the units of length, width, and height are different then, we need to convert them into the same unit first and then find the volume.
3. What is the formula for the volume of cube and cuboid?
The volume of the cuboid is the product of length, width, and height.
Volume of cuboid = lbh
Volume of cube = s × s × s
Must Read: