Whole Numbers is a part of a number system that includes all the positive integers from 0 to infinity. These numbers are present on the number line and are usually called real numbers. Thus, we can say that Whole Numbers are Real Numbers but not all Real Numbers are Whole Numbers. Complete Set of Natural Numbers including “0” are called Whole Numbers.
Whole Numbers – Definition
Whole Numbers are numbers that don’t have fractions and is a collection of positive integers including zero. It is denoted by the symbol “W” and is given as {0, 1, 2, 3, 4, 5, ………}. Zero on a whole denotes null value or nothing.
- Whole Numbers: W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10……}
- Natural Numbers: N = {1, 2, 3, 4, 5, 6, 7, 8, 9,…}
- Integers: Z = {….-9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,…}
- Counting Numbers: {1, 2, 3, 4, 5, 6, 7,….}
Whole numbers are positive integers along with zero and don’t have fractional or decimal parts. You can perform all the basic operations such as Addition, Subtraction, Multiplication, and Division.
Symbol
The Symbol to denote the Whole Numbers is given by the alphabet W = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…
- All-natural numbers are whole numbers
- All positive integers including zero are whole numbers
- All whole numbers are real numbers
- All counting numbers are whole numbers
Properties of Whole Numbers
Whole Numbers Properties depend on arithmetic operations such as Addition, Subtraction, Multiplication, Division. When you multiply or add two whole numbers the result will always be a Whole Number. If you Subtract Two Whole Numbers the result may not always be a Whole Number and it can be an Integer too. Division of Whole Numbers can result in a Fraction at times. Let us see few more Properties of Whole Numbers by referring below.
Closure Property: Whole Numbers can be closed under addition or multiplication. If a, b are two whole numbers then a.b and a+b is also a whole number.
Commutative Property of Addition and Multiplication: Sum and Product of Two Whole Numbers will be the same no matter the order in which they are added or multiplied. If a, b are two whole numbers then a+b = b+a, a.b = b.a
Additive Identity: If a Whole Number is added to 0 the result remains unchanged. If a is a whole number then a+0 = 0+a = a
Multiplicative Identity: Whenever you multiply a whole number with 1 the result remains unchanged. Let us consider a whole number “a” then a.1 = 1. = a
Associative Property: If you are grouping the whole numbers and adding or multiplying a set the result remains the same irrespective of the order. If a, b, c are whole numbers then a + (b + c) = (a + b) + c and a. (b.c)=(a.b).c
Distributive Property: If a, b, c are three whole numbers then the distributive property of multiplication over addition is given by a.(b+c) =(a.b)+(a.c), Similarly Distributive Propoerty of Multiplication over Subtraction is given by a.(b-c) = (a.b)-(a.c)
Multiplication by Zero: If you multiply a Whole Number with Zero the result is always zero. i.e. a.0=0.a=0
Division by Zero: If you divide a Whole Number with Zero the result is undefined, i.e. a divided by 0 is not defined.
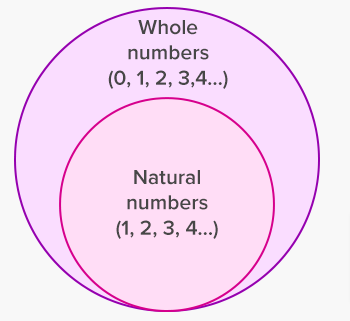
Difference between Natural Numbers and Whole Numbers
| Whole Numbers | Natural Numbers |
| Whole Numbers: {0, 1, 2, 3, 4, 5, 6,…..} | Natural Numbers: {1, 2, 3, 4, 5, 6,……} |
| All whole numbers are not natural numbers | All Natural numbers are whole numbers |
| Counting starts from 0 | Counting starts from 1 |
By referring to the below sections you will better understand the difference between Whole Numbers and Natural Numbers.
Solved Examples on Whole Numbers
1. Are 101, 147, 193, 4028 whole numbers?
Yes, 101, 147, 193, 4028 are all whole numbers.
2. Solve 8 × (3 + 12) using the Distributive Property?
We know as per the Distributive Property a.(b+c) =(a.b)+(a.c)
Applying the Input Numbers in the formula we have the equation as such
8 × (3 + 12) = 8*3 +8*12
= 24+108
= 132
FAQs on Whole Numbers
1. Is 0 a Whole Number?
Yes, 0 is a Whole Number.
2. What is the Symbol of Whole Numbers?
The Letter W represents the Whole Numbers.
3. Are all Natural Numbers Whole Numbers?
Yes, all Natural Numbers are Whole Numbers but not all Whole Numbers are Natural Numbers. Natural Numbers begin from 0 and counts till infinity. Whole Numbers begin from 0 and end at infinity.
4. What is the set of whole numbers?
The whole numbers are the natural numbers together with 0. The set of whole numbers is a subset of the integers but does not include the negative integers.