Check Word Problems On Pythagorean Theorem in the below sections. Refer Pythagorean Theorem Study Material along with the solutions and steps to solve them. Get various model questions on Pythagoreans theorem and improve your mathematical knowledge along with other math skills. Know the shortcuts, tips, and tricks to solve Pythagorean Theorem Problems. Assess your preparation standard taking the help of the Pythagorean Theorem Questions available and cross-check your solutions here.
How to Solve Problems on Pythagorean Theorem?
Follow the simple steps listed here to solve problems related to the Pythagorean Theorem. They are along the lines
Step 1: Look at all the terms in the final equation
Step 2: Find out which right triangles contain those terms
Step 3: Start with those right triangles and apply the Pythagorean Theorem
Pythagorean Theorem Word Problems
Problem 1:
A 35-foot ladder is leaning against the side of a building and its positioned such that the base of the ladder is 21 feet from the base of the building. Find the distance above the ground where the point of the ladder touches the building?
Solution:
Let the point above the ground = x
As given in the question,
Length of the foot ladder = 35
Base of the ladder = 21 feet
Let the equation be a² + b² = c²
(21)² + (x)² = (35)²
441 + x = 1225
Subtracting by 441 on both sides
x = 784
Squaring and both sides
x = √784
x = 28
28 feet far above the ground is the point where the ladder touches the building.
Problem 2:
Lainey runs a string of lights from the ground straight up a door frame that is 2.5 meters tall. Then they run the rest of the string in a straight line to a point on the ground that is 6 meters from the base of the door frame. There are 10 lights per meter of a string. How many total lights are on the string?
Solution:
As given in the question,
The length of the lights = 2.5 meters
The base of the door frame = 6 meters
No of lights per meter = 10
To find the total number of lights on a string, we write the equation
h² = (2.5)² + (6)²
h²= 6.25 + 36
h²= 42.25
h = √42.25
String Length = 2.5 + √42.25
Therefore, no of lights = 9m * 10 lights = 90 lights
Thus, the total lights on the string = 90 lights
Problem 3:
Fencing at a hardware store costs $16.97 per yard. How much would it cost to fence in a triangular-shaped yard that has a leg of 11 feet and another leg of 60 feet?
Note: The yard is in the shape of a right triangle.
Solution:
Amount of fencing at hardware store = $16.97 per yard
Length of one leg = 11 feet
Length of another leg = 60 feet
As given the yard is in the shape of right triangle
We know the equation,
a² + b² = c²
(11)² + (60)² = c²
121 + 3600 = c²
3721 = c²
Squaring on both sides
√3721 = √c²
61 = c
The amount for a fence in a triangular-shaped yard = $61
Thus, the final solution is $61
Problem 4:
If a 34-foot ladder is placed against the top of a 30-foot building. How many feet will be at the bottom of the ladder from the bottom of the building?
Solution:
As given in the question,
Length of the ladder = 34 foot
Length of the building = 30 foot
Let the length of bottom of the ladder = x
a² + b² = c²
(30)² + x² = (34)²
900 + x² = 1156
x² = 256
Add square root on both sides
√x² = √256
x = 16 feets
Therefore, the bottom of the ladder from the bottom of the building will be 16 feets
Thus, the final solution is 16 feet
Problem 5:
A certain television is advertised as a 34-inch TV. If the width of the TV is 30 inches, how many inches tall is the TV?
Solution:
As given in the question,
Size of the TV = 34 inch
Width of the TV = 30 inch
Length of TV = x
To know the length of TV, we have to find the equation
a² + b² = c²
(30)² + x² = (34)²
900 + x² = 1156
Add square root on both sides
√x² = √1156
x = 34
TV is 34 inches tall.
Thus, the final solution is 34 inches
Problem 6:
Ramu starts driving north for 9 miles, then takes a right turn, and then he drives east for another 40 miles. At the end of driving, what is the distance of a straight line from the starting point?
Solution:
As given in the question,
Driving for north = 9 miles
Driving for east =40 miles
Let the straight line distance = x
The equation will be
a² + b² = c²
(9)² + (40)² = c²
81 + 1600 = c²
1681 = c²
Add square roots on both sides
√1681 = √c²
41 = c
Therefore, the straight line distance from the starting point is 41 miles
Thus, the final solution is 41 miles
Problem 7:
In a right-angled triangle, the hypotenuse square is equal to the sum of the squares of other two sides?
Solution:
Given: A right-angle triangle in which one of the sides is 90°
To prove: AC² = AB² + BC²
Construction: Draw BD ⊥ AC
In Δ’s ADB and ABC
∠ADB = ∠ABC (Each 90°)
∠A = ∠A (Common)
ΔADB ∼ ΔABC (By A-A Criteria)
AD/AB = AB/AC
AB² = AD * AC is the first equation
In Δ’s BDC and ABC
∠CDB = ∠ABC (Each 90°)
∠C = ∠C (Common)
ΔBDC ∼ ΔABC (By A-A Criteria)
DC/BC = BC/AC
BC² = AC * DC is the (2) equation
AB² = AD * AC is the (3) equation
Adding the equations (1) and (2)
AB² + BC² = AD * AC + AC * AD
AB² + BC² = AC (AD + DC)
AB² + BC² = AC (AC)
AB² + BC² = AC²
∴ Hence proved
Problem 8:
In the triangle, if the square of one side of the triangle is equal to the sum of the squares of another two sides of the triangle, then the angle that is opposite to the first side is a right angle triangle?
Solution:
Given: ΔABC such that AB² + BC² = AC²
To prove: ∠B = 90°
Construction: Draw ΔDEF such that DE = AB, EF = BC and ∠E = 90°
Since ΔDEF is right-angled,
By Pythagoras theorem
DE² + EF² = DF²
AB² + BC² = DF² (By const DE = AB and EF = BC)
AC² = DF² (Given AB² + BC² = AC²)
AC = DF
To prove: ∠B = 90°
In Δs ABC and DEF
AB = DE (By const)
BC = EF (By const)
AC = DF (Proved)
ΔABC ≅ ΔDEF (SSS)
∠B = ∠E = 90°
ΔABC is a right triangle
Problem 9:
Mary wants to cut across a rectangular lot rather than walk around it. Of the lot is 120 feet long and 50 feet wide. Mary walks diagonally across the lot, how many feet is the short cut?
Solution:
As given in the question,
Length of the lot = 120 feet
Width of the lot = 50 feet
Let the shortcut distance be x
As per the Pythagorean theorem,
a² + b² = c²
(50)² + (120)² = x²
2500 + 14,400 = x²
16,900 = x²
130 = x
Therefore, Mary walks 130 feet shortcut
Thus, the final solution is 130 feet
Problem 10:
The length of a living room is 2 feet less than twice its width. If the diagonal is 2 feet more than twice the width, find the dimensions of the room?
Solution:
Let the width of the living room = x
Given that
Length of the living room = 2 feet less than twice its width
Diagonal = 2 feet more than twice the width
From the given equations,
Width represents x² + (2x – 2)² = (2x + 2)²
Length represents x² = (2x + 2)² – (2x-2)²
From both the equations,
x² = (4x + 8x + 4) – (4x – 8x + 4)
x² = 16x
(x²-16x) = 0
x(x-16) = 0
x = 0, x=16
Therefore, the width = 16
Length = (2x – 2) = 2(16) – 2 = 30
Thus, the length of the living room = 30 feet
Width = 16 feet
Hence, the final solution is l = 30 feet and w = 16 feet
Problem 11:
A man goes 12m east and 9m north. Find the distance from the initial point?
Solution:
As given in the question,
The distance man goes to east = 12m
i.e., BC = 12m
The distance man goes to north = 9m
i.e., AB = 9m
To find the initial point (AC), apply the Pythagorean theorem
AC² = AB² + BC²
AC² = (9)² + (12)²
AC² = 81 + 144
AC² = 225
AC = √225
AC = 15
Therefore, he is 15m far from his initial point
Thus, the final solution is 15m
Problem 12:
Hari wants to hang a 7m long banner from the roof of her shop. The hooks for the strings are 10m apart. Hari wants the top of the banner to hang 1m below the roof. How long should each of the strings be?
Solution:
As per the question,
Length of the long banner = 7m
Hooks for strings = 10m apart
Length where the banner to hang below the roof = 1m
Let the length of the string = x
Hence, the equation will be
7 + 2x = 10
2x = 3
x = 1.5
Now, apply the Pythagorean theorem,
C² = (1)² + (1.5)²
C² = 1 + 2.25
C² = 3.25
C = √3.25
C = 1.80
Hence, each string should be 1.80m
Thus, the final solution is 1.80m
Problem 13:
Two kids are flying a kite with a string of 50 meters long. If the kids are 35 meters apart, how high is the kite off the ground?
Solution:
As given in the question,
Length of the string = 50 meters
The distance of kids apart = 35 meters
The height of the kite off the ground = b
Applying the Pythagorean theorem, we get
a² + b² = c²
(35)² + b² = (50)²
1225 + b² = 2500
b² = 1275
b = √1275
b = 35.70
Therefore, 35.70m is the kite off the ground
Thus, the final solution is 35.70 m
Problem 14:
A carpenter needs to add 2 braces to a barn door. If the door measures 12 * 16 feet, how much wood will he need for both braces?
Solution:
As given in the question,
No of braces = 2
Length of the door = 12 feet
The breadth of the door = 16 feet
To find the amount of wood for braces, we apply Pythagorean theorem
a² + b² = c²
(12)² + (16)² = c²
144 + 256 = c²
400 = c²
c = √400
c = 20
Amount of wood for both the braces = 2 * 20 = 40ft
Therefore, the carpenter requires 40 ft of wood for both the braces.
Thus, the final solution is 40 ft
Problem 15:
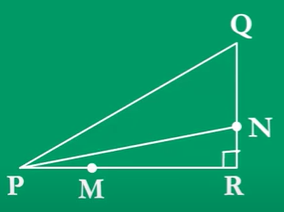
M and N are points on the sides RP and RQ respectively of triangle PQR right-angled at R. Prove that PN² + QM² = PQ² + MN²?
Solution:
PN² = PR² + RN² is the (1) equation
QM² = MR² + RQ² is the (2) equation
Adding the equation (1) and (2)
PN² + QM² = MR² + RQ² + PR² + RN²
PN² + QM² = (MR² + RN²) + (RQ² + PR²)
PN² + QM² = MN² + PQ²
∴ Hence, it is proved
