Students can use the Worksheet on Area of the Path to learn how to find the area of a path? Subject Experts have designed these Printable Area of the Path Worksheets so that you can use them to self-examine your level of preparation. Solve the different models of questions available in the Area of Path Worksheets and master the topics. Become proficient and enhance your problem-solving skills with the step-by-step solutions provided for all the problems available.
See More: Area of the Path
Area of Path Worksheets PDF with Solutions
I. There is a hall 80 m in length and 40 m in breadth. There is a lawn 7 m wide surrounding the hall on all four sides outside. Find the area of the lawn.
Solution:
First, let us draw the diagram based on the given details.
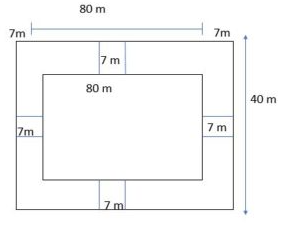
The hall is a rectangle. The hall and lawns which are outside are a bigger rectangle.
Then length of bigger rectangle = 80 + 7 + 7
= 94 m
Breadth of bigger rectangle = 40 + 7 + 7
= 54 m
Area of hall and Lawns = 94 x 54
= 5076 m2
Area of the hall = 80 x 40= 3200 m2
Area of Lawns = 5076 – 3200= 1876 m2
Therefore, the area of the lawn is 1876 m2.
II. A square-shaped house is surrounded by a path 20 cm wide around it. If the area of the path is 4000 cm², find the area of the square-shaped house?
Solution:
In the figure,
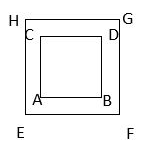
ABCD is a square-shaped house.
EFGH is the outer boundary of the path.
Let each side of the square shaped house is = x cm
Then, the area of the square shaped houseABCD (x × x) cm² = x² cm²
Now, the side of the square EFGH = (x + 20 + 20) cm = (x + 40) cm
So, the area of square EFGH = (x + 40) (x + 40) cm² = (x + 40)² cm²
Therefore, area of the path = Area of EFGH – Area of ABCD
= [(x + 40)² – x²] cm²
= [x² + 1600 + 80x – x²] cm²
= (80x + 1600) cm²
But the area of path given = 4000 cm²
Therefore, 80x + 1600 = 4000
80x = 4000 – 1600
80x = 2400
x = 2400/80 = 30
side of square shaped house =30 cm
Therefore, the area of the square-shaped house = 30 × 30 cm² = 900 cm².
III. Find the area of the shaded portion in the below figure.
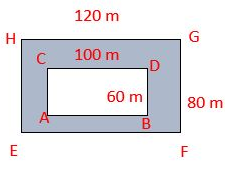
Solution:
Area of the shaded portion= Area of rectangle HGFE – Area of rectangle CDBA
Area of rectangle CDBA :
Length (CD) = 100 m
Breadth (BD) = 60 m
Area of rectangle CDBA = Length x width
= 100 x 60
= 6000 m²
Area of rectangle HGFE :
Length (HG) = 120 m
Breadth (GF) = 80 m
Area of rectangle HGFE = Length x width
= 120 x 80
= 9600 m²
Area of the shaded portion
= Area of rectangle HGFE – Area of rectangle CDBA
= 9600 m² – 6000 m²
= 3600 m²
Therefore, the Area of the shaded portion is 3600 m².
IV. A rectangular lawn of length 80 m and breadth 20 m is to be surrounded externally by a path that is 5 m wide. Find the cost of turfing the path at the rate of Rs 5 per m²?
Solution:
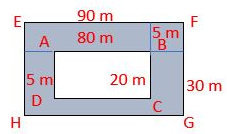
Length of the lawn = 80 m
Breadth of the lawn = 20 m
Area of the lawn = (80 × 20) m²
= 1600 m²
Length of lawn including the path = [80 + (5 + 5)] m = 90 m
Breadth of the lawn including the path = [20 + (5 + 5)] m = 30 m
Area of the lawn including the path = 90 m × 30 m = 2700 m²
Therefore, area of the path = (2700 – 1600) m² = 1100 m²
For 1 m², the cost of turfing the path = Rs 5
For 1100 m², the cost of turfing the path = Rs 1100 × 5 = Rs 5500.
Therefore, The cost of turfing the path is Rs 5500.
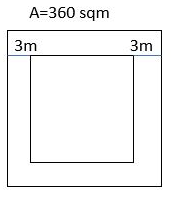
V. A square lawn is surrounded by a path 3 m wide. If the area of the path is 360 m², find the area of the lawn?
Solution:
Given that,
Area of the path=360 m²
Let the side of the lawn be a meters.
Area of lawn=a²
Length of outer side=(a+3+3)m=(a+6)m
Area of outer square=(a+6)2
=a²+36+12a
Area of path=Area of outer square-area of lawn
360=a²+36+12a – a²
360 = 12a + 36
12(a+3) = 360
a+3 = 360/12
a+3=30
a=30-3
a= 27 m
The area of the lawn is= 27 × 27= 729 m.
VI. Three square flowerbeds each of sides 4 m are dug on a piece of land 15 m long and 5 m wide. Find the area of the remaining portion of the land. Find the cost of leveling this land at the rate of Rs 5 per 100 cm²?
Solution:
Given that,
Sides of flower beds=4m
Length of a dug piece of land=15 m
width of a dug piece of land=5 m
cost=5 per 100 cm²
Area of Three flower beds=area of square=side2
=3 × side2
=3 × 42
=48 m²
Area of land=Area of Rectangle=l × b
=15 × 5
=75 m²
Remaining portion=area of land – area of four flower beds
=75 m² – 48m²
=27 m²
=27 × 100 × 100 cm²=270000 cm²
Then, the cost of leveling this land at the rate of Rs 5 per 100 cm²,
= 270000 × 5/100
= 2700 × 5
=13500
Therefore, the cost of leveling the land is Rs 13,500.
VII. A rectangular field is of dimension 40 m x 20 m. Two paths run parallel to the sides of the rectangle through the center of the field. The width of the longer path is 2m and that of the shorter path is 1 m.
Find (i) the area of the paths
(ii) the area of the remaining portion of the field
(iii) the cost of constructing the roads at the rate of Rs 20 per sq.m.
Solution:
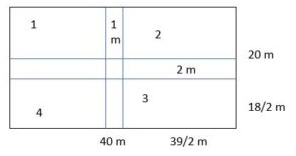
Length of the rectangular field L = 40 m
Breadth B = 20m
Area = L x B
=40 m x 20 m
Area of outer rectangle = 800 m2
Area of inner small rectangle = 39/ 2 x 18/ 2 = 175.5 cm
(i) Area of the path = Area of the outer rectangle – Area of 4 inner small rectangles
= (800 – 4(175.5))m2
= (800 – 702) m2
= 98 m2
Therefore, Area of path=98m2
(ii) Area of the remaining portion of the field = Area of the outer rectangle – Area of the paths
= (800 – 98) m2
= 702 m2
Therefore, the Area of the remaining portion of the field is 702m2.
(iii) Cost of constructing 1 m2 road = Rs 20
Cost of constructing 98 m2 road = Rs 20 x 98
= Rs 1960
Therefore, the cost of constructing the road is Rs 1960.
VIII. A grassy plot is 200 m x 80 m. Two cross paths each 7 m wide are constructed at right angles through the center of the field, such that each path is parallel to one of the sides of the rectangle. Find the total area used as a path?
Solution:
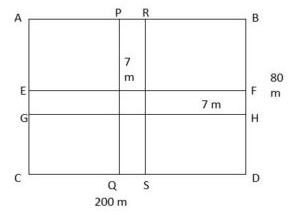
Given that,
A grassy plot is 200 m x 80 m.
Two cross paths each 7 m wide are constructed at right angles through the center of the field.
Area of the longer path (EFGH) = 200 x 7= 1400
Area of the shorter path (PQRS) = 7 x 80 = 560
Area of the centre field (IJKL) = 7 x 7 = 49
Area of the path = (Area of the longer path + Area of the shorter path – Area of the center field)
=1400 + 560 – 49
= 1960 – 49 = 1911 m².
Hence, The total area used as the path is 1911 m².
IX. A floor is 18 m long and 8 m wide. A square carpet of side 8 m is laid on the floor. Find the area of the floor not carpeted?
Solution:
Given that,
Length of the floor=18 m
The breadth of the floor=8 m
Side of the square=8m
Area of the square=side2
=82=64 sq m
Area of the rectangle=length x breadth
=18 x 8
=144 sq m
The area of floor not carpeted = Area of the floor – Area of carpet
= 144 – 64 = 80 m²
Therefore, the area of the floor not carpeted is 80 m².