Related angles are nothing but the pairs of angles and assigned with specific names that we come across. Related angles have some conditions to mention. Learn the detailed concept of Related angles with images and examples in this article. Improve your preparation level by reading the entire concept without missing any subtopic. We have given complete information about Lines and Angles on our website for free of cost.
Different Types of Related Angles
Check different types of Related Angles along with examples to clearly understand the concept. We have explained each of them with definitions, solved examples, etc. Refer to the following modules and get a grip on it.
Complementary Angles
If the sum of the measures of two angles is about 90°, those angles are called complementary angles.
Facts of Complementary Angles
- The two right angles never complement each other.
- Also, the two obtuse angles never complement each other.
- Two complementary angles are always acute but there is no possibility of vice versa.
Example:
Let us take two angles which are complementary angles. If one angle is a, then the other angle is 90° – a.
An angle of 40° and another angle of 50° are complementary angles of each other.
Also, complement of 40° is 90° – 40° = 50°.
And complement of 50° is 90° – 50° = 40°
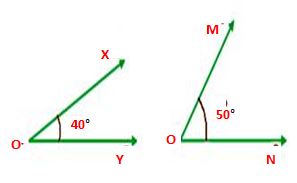
The ∠XOY is 40° and ∠MON is 50°. By adding two angles ∠XOY and ∠MON, we get 90° as they are the Complementary Angles.
Therefore, the sum of the ∠XOY and ∠MON is 90°
∠XOY + ∠MON = 90°.
Supplementary Angles
Supplementary Angles are the angles when the sum of the measures of two angles is 180°. If the sum of the two angles forms a straight angle, then those angles are called Supplementary Angles. If one angle is a, then the other angle is 180° – a.
Example:
Let us take two angles which are Supplementary angles. If one angle is x, then the other angle is 180° – x.
An angle of 110° and another angle of 70° are supplementary angles of each other. Also, a supplement of 110° is 180° – 110° = 70°.
And the supplement of 60° is 180° – 70° = 110°.
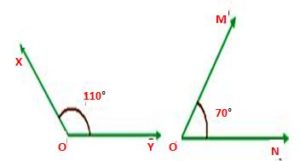
From the above figure, the ∠XOY is 110° and ∠MON is 70°. By adding two angles ∠XOY and ∠MON, we get 180° as they are the Supplementary Angles.
Therefore, the sum of the ∠XOY and ∠MON is 180°
∠XOY + ∠MON = 180°.
Adjacent Angles
The two angles are called to be Adjacent angles when they have a common arm, a common vertex, and also the non-common arms present on the opposite side of the common arm.
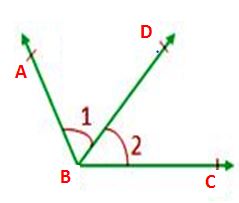
From the above figure, ∠ABD and ∠CBD are adjacent angles with the common arm BD. The B is the common vertex and BA, BC is opposite sides of BD.
Linear Pair
When two adjacent angles form a linear pair of angles with the non-common arms are two opposite rays. In other words, the sum of two adjacent angles is 180°.
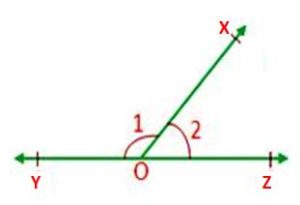
From the above figure, the ∠XOY and ∠XOZ are two adjacent angles. By adding two angles ∠XOY and ∠XOZ, we get 180°.
Therefore, the sum of the ∠XOY and ∠XOZ is 180°
∠XOY + ∠XOZ = 180°.
Vertically Opposite Angles
The arms of the lines are opposite in direction and both lines are interesting to each other in Vertically opposite angles. The pair of vertically opposite angles are equal.
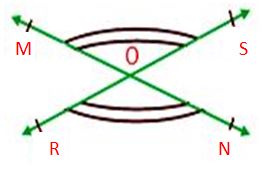
From the above figure, the ∠MOR and ∠SON and ∠MOS and ∠RON are pairs of vertically opposite angles.
Theorems on Related Angles
1. If a ray stands on a line, then the sum of adjacent angles formed is 180°.
Given: A ray BE standing on (AC) ⃡ such that ∠ABE and ∠CBE are formed.
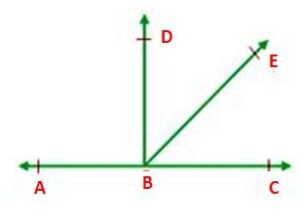
Construction: Draw BD ⊥ AC.
Proof: Take the angle ABE.
Now ∠ABE = ∠ABD + ∠DBE ……………. (1)
Take the angle CBE.
Also ∠CBE = ∠CBD – ∠DBE ……………. (2)
Now, add equation 1 and equation 2.
Adding (1) and (2),
∠ABE + ∠CBE = ∠ABD + ∠CBD + ∠DBE – ∠DBE
∠DBE – ∠DBE = 0
= ∠ABD + ∠CBD
∠ABD = 90°; ∠CBD = 90°
Substitute ∠ABD and ∠CBD values in ∠ABD + ∠CBD
= 90° + 90°
= 180°
2. The sum of all the angles around a point is equal to 360°.
Given: A point O and rays OA, OB, OC, OD, OE which make angles around O.
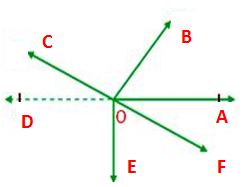
Construction: Draw OD opposite to ray OA
Proof: Since, OB stands on DA therefore
∠AOB + ∠BOD = 180°
∠BOD = ∠BOC + ∠COD
Substitute ∠BOD = ∠BOC + ∠COD in ∠AOB + ∠BOD = 180°
∠AOB + (∠BOC + ∠COD) = 180°
∠AOB + ∠BOC + ∠COD = 180° ……………. (i)
Again OE stands on DA, therefore
∠DOE + ∠EOA = 180°
∠EOA = ∠EOF + ∠FOA
Substitute ∠EOA = ∠EOF + ∠FOA in ∠DOE + ∠EOA = 180°
∠DOE + (∠EOF + ∠FOA) = 180°
∠DOE + ∠EOF + ∠FOA = 180° ……………. (ii)
Now, add euqtion (i) and equation (ii)
Adding (i) and (ii),
∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOF + ∠FOA
= 180° + 180°
= 360°
3. If two lines intersect, then vertically opposite angles are equal.
Given: MN and AB intersect at point O.
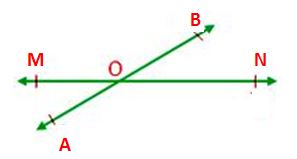
Proof: OB stands on MN.
Therefore, ∠MOB + ∠BON = 180° ……………. (i)
MO stands on AB
∠MOB + ∠MOA = 180° ……………. (ii)
From (i) and (ii),
∠MOB + ∠BON = ∠MOB + ∠MOA
∠BON + ∠MOA
Similarly, ∠MOB = ∠AON can be proved.