Learn what are Vertically Opposite Angles and how to calculate them in this article. Vertically Opposite Angles are the angles formed when two lines intersect each other. The vertically opposite angles are always equal to each other. The adjacent angles of vertically opposite angles are always supplementary angles and they form 180º when we add them. Find Lines and Angles concepts and problems on our website.
If one angle is 35º, then the other angle is 180º – 35º.
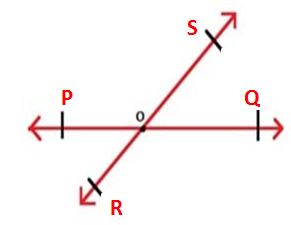
From the above figure, the line segment PQ and RS meet at the point O and these two lines are intersecting lines.
In a pair of intersecting lines, the angles which are opposite to each other form a pair of vertically opposite angles. From the figure, ∠SOQ and ∠POR form a pair of vertically opposite angles.
∠SOQ = ∠POR
∠SOP = ∠ROQ
Note: A vertical angle and its adjacent angle is supplementary to each other. It means they add up to 180 degrees.
Vertical Angles Theorem and Proof
Theorem: In a pair of intersecting lines the vertically opposite angles are equal.
Proof: Consider two lines PQ and RS which intersect each other at O. The two pairs of vertical angles are:
i) ∠SOQ = ∠POR
ii) ∠SOP = ∠ROQ

It can be seen that ray OS stands on the line PQ and according to Linear Pair Axiom, if a ray stands on a line, then the adjacent angles form a linear pair of angles.
Therefore, ∠SOQ + ∠SOP = 180° —(1) (Linear pair of angles)
Similarly, Ray OP stands on the line SR.
Therefore, ∠SOP + ∠POR = 180° —(2) (Linear pair of angles)
From (1) and (2),
∠SOQ + ∠SOP = ∠SOP + ∠POR
⇒ ∠SOQ = ∠POR —(3)
Also, OQ stands on the line SR.
Therefore, ∠SOQ + ∠QOR = 180° —(4) (Linear pair of angles)
From (1) and (4),
∠SOQ + ∠SOP = ∠SOQ + ∠QOR
⇒ ∠SOP = ∠QOR —(5)
Thus, the pair of opposite angles are equal.
Hence, proved.
Vertically Opposite Angles Examples
1. In the given figure, find the measure of unknown angles.
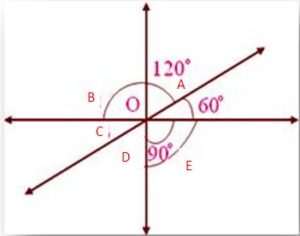
Solution:
From the given figure
(i) ∠C = 60° vertically opposite angles
(ii) ∠B = 90° vertically opposite angles
(iii) ∠B + ∠A + 60° = 180° (straight angle)
90° + ∠ A + 60° = 180°
150° + ∠ A = 180°
Therefore, ∠A = 180° – 150° = 30°
(iv) ∠A = ∠D vertically opposite angles
Therefore, ∠D = 30°
2. In the given figure, lines AB, CD, EF intersects at O. If M : N : P = 1 : 2 : 3, then find the values of M, N, P.
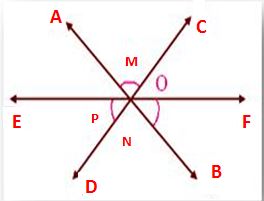
Solution:
We know that the sum of all the angles at a point is 360°.
∠AOC = ∠DOB = M° (Pair of vertically opposite angles are equal.)
∠FOB = ∠AOE = N° (Pair of vertically opposite angles are equal.)
∠EOD = ∠COF = P° (Pair of vertically opposite angles are equal.)
Therefore, ∠AOE + ∠AOC + ∠COF + ∠FOB + ∠BOD + ∠DOE = 360°
N + M + P + N + M + P = 360°
⟹ 2M + 2N + 2P = 360°
⟹ 2(M + N + P) = 360°
⟹ M + N + P = 3̶6̶0̶°/2̶
⟹ M + N + P = 180° ——— (i)
Let the common ratio be a.
Therefore, M = a, N = 2a, P = 3a
Therefore, from the equation (i) we get;
a + 2a + 3a = 180°
⟹ 6a = 180°
⟹ a = 1̶8̶0̶°/6̶
⟹ a = 30°
Therefore, M = a, means M = 30°
N = 2a, means N = 2 × 30 = 60°
P = 3a, means P = 3 × 30 = 90°
Therefore, the measures of the angles are 30°, 60°, 90°.