Know the congruent shapes, definitions, and examples here. Check the angles and how they work for each triangle shape. Follow the different cases where the lines and angles are said to be congruent. Get the definition of congruency in analytic geometry. Understand the concept of congruent with the detailed explanation in the next sections. You can know the brief details about how congruency works for each shape.
Are you about congruent topics? If so, Don’t worry! You can get the exact content that you are exploring for. Go through the next sections to check the complete details regarding congruent statements and figures. We are providing the detailed concept with the help of examples. Check it out!!
Do Check:
Congruent Shapes – Definition
Two figures or objects are said to be congruent if one of them is a mirror image of the other or if both of them have the same shape and size.
Geometrically, when considering a 2 Dimensional object, a set of two points are said to be congruent when one point can be transformed either by translation, rotation, or reflection. This is called a combination of rigid motions or Isometry. In simple terms, we can define this as repositioning or reflecting an object so that it coincides perfectly with some other object without changing its size. Some of the examples of congruency are
- Two line segments are said to be congruent if the length of both the lines is the same.
- Two angles are said to be congruent if the angle is the same for both the angles on some common line.
- Two circles are said to be congruent if the diameter of both circles is the same.
Different figures follow different criteria to be congruent. For example
- If two triangles are needed to be congruent then three sides of one triangle should be equal to three sides of another triangle.
- If two rectangles are needed to be congruent then they must possess equal opposite sides for both the rectangles.
- If two squares are needed to be congruent then they must have all sides equal for both the squares.
In simple terms, congruency can be defined as two figures trying to prove in either of the ways that they are twins.
Congruency in Different Figures
Different figures follow different criteria to test their congruency. We consider diameter to test congruency of circle and lines to test congruency of triangles etc.
Triangle
Case 1: Equal sides for a triangle(SSS: side, side, side)
Two triangles are said to be congruent if they possess all equal sides.
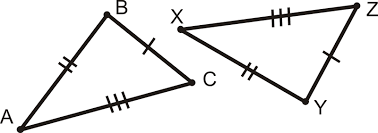
Here, in the above figure, ABC is one triangle and XYZ is another triangle.
As we observe both the triangles, side AB is equal to side XY. AB=XY.
Side AC is equal to side XZ. AC=XZ.
Side BC is equal to side YZ. BC=YZ.
Here, we observe that all three sides of one triangle are equal to the other. This satisfies the SSS(side,side,side) criteria for congruency.
Therefore we can say that these triangles are congruent.
Case 2: Two equal angles and the corresponding side of a triangle(ASA: angle, side, angle)
Two triangles are said to be congruent if they possess two equal angles and a corresponding side.
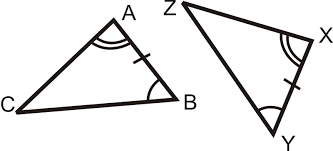
Here, in the above figure, ABC is one triangle and DEF is another triangle.
As we observe both the triangles, side AB is equal to side XY. AB=XY.
Angle B is equal to angle Y. Angle ABC=Angle XYZ.
Angle A is equal to angle X. Angle CAB=Angle ZXY.
Here two angles and the corresponding side of one triangle is equal to two angles and the corresponding side of another triangle. This satisfies the ASA(angle, side, angle) criteria for congruency.
Therefore we can say that these triangles are congruent.
Case 3: Two equal sides and the corresponding angle of a triangle(SAS: side, angle, side)
Two triangles are said to be congruent if they possess two equal sides and a corresponding angle.
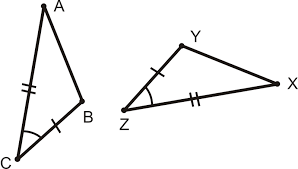
Here, in the above figure, ABC is one triangle and XYZ is another triangle.
As we observe both the triangles, side BC is equal to side YZ. BC=YZ.
Side AC is equal to side ZX. AC=ZX.
Angle C is equal to angle Z. Angle ACB=Angle YZX.
Here two sides and the corresponding angle of one triangle is equal to two sides and the corresponding angle of another triangle. This satisfies the SAS(side, angle, side) criteria for congruency.
Therefore we can say that these triangles are congruent.
Rectangle
Two rectangles are said to be congruent if opposite sides are equal and the adjacent sides maintain an angle of 90 degrees.
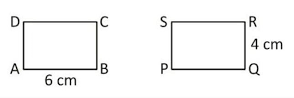
Here in the above figure, ABCD is one rectangle and PQRS is another rectangle.
We observe that in rectangle ABCD AB=CD and in rectangle PQRS PQ=RS.
We also observe that AB=CD=PQ=RS.
We observe that in rectangle ABCD BC=AD and in rectangle PQRS QR=SP.
We also observe that BC=AD=QR=SP.
In rectangle ABCD, the angle between AB and AD is 90 degrees and also, in rectangle PQRS angle between PQ and PS is 90 degrees.
Therefore we can say that both these rectangles are congruent.
Polygon
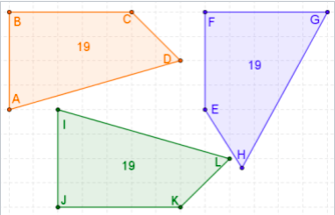
From the above diagram of quadrilaterals, the orange and green are said to be congruent whereas blue is not the congruent one. Though all three quadrilateral has a similar perimeter. The ordering of blue quadrilateral sides is “mixed” and it results in one of the diagonals and two of the interior angles not being congruent.
If two polygons are to be congruent, they should have an equal number of sides and vertices. If a polygon has n sides and if they are said to be congruent if and only if they are numerically identical sequences which are side-angle-side-angle for n number of sides and n number of angles.
Polygons Congruency can be established by following some specific rules:
- In the first step, you have to match and label the opposite or corresponding vertices of both the figures.
- Then, you have to draw a vector from one vertex of one figure to the opposite vertex of another figure.
- Translate the vector of the first figure such that it matches the two vertices.
- Then, you have to rotate the figure formed in the above step until the matched vertex one pair matches with the corresponding sides.
- Reflect the translated figure in the above step to the matched side until it matches the figure.
- If any of the steps cannot be done, then we declare that polygons are not congruent.
Hence the congruency of the polygons can be found out.