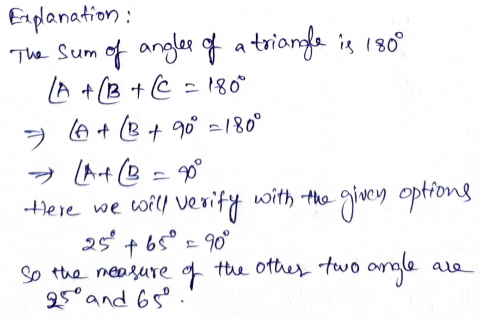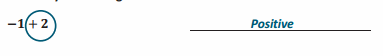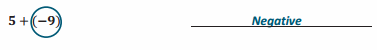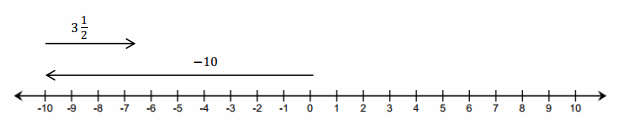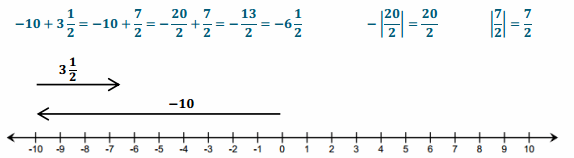Prasanna – CCSS Answers

Decimal Place Value Chart: Definition, How to Write, and Examples

March 20, 2024March 20, 2024 by Prasanna

Mathematics is the study of numbers, shapes, and patterns. It includes various complex and simple arithmetic topics that help people in their daily life routine. In Maths, Numbers play a major role and they can be of different types like Real Numbers, Whole Numbers, Natural Numbers, Decimal Numbers, Rational Numbers, etc. Today, we are going to discuss one of the main topics of Decimal Numbers. In Decimals, identifying the Decimal Place Values is a fundamental topic and everyone should know the techniques clearly. So, here we will be discussing elaborately the topic of Decimal Place Values Chart.

Let’s get into it.

What is a Decimal in Math?

In algebra, a decimal number can be represented as a number whose whole number part and the fractional part is divided by a decimal point. The dot in a decimal number is called a decimal point. The digits following the decimal point show a value smaller than one.

What is the Place Value of Decimals?

Place value is a positional notation system where the position of a digit in a number, determines its value. The place value for decimal numbers is arranged exactly the identical form of treating whole numbers, but in this case, it is reverse. On the basis of the preceding exponential of 10, the place value in decimals can be decided.

Decimal Place Value Chart

Decimal Place Value Chart table image

On the place value chart, the numbers on the left of the decimal point are multiplied with increasing positive powers of 10, whereas the digits on the right of the decimal point are multiplied with increasing negative powers of 10 from left to right.

The first digit after the decimal represents the tenths place.
The second digit after the decimal represents the hundredths place.
The third digit after the decimal represents the thousands place.
The rest of the digits proceed to fill in the place values until there are no digits left.

How to write the place value of decimals for the number 132.76?

The place of 6 in the decimal 132.76 is 6/100
The place of 7 in the decimal 132.76 is 7/10
The place of 2 in the decimal 132.76 is 2
The place of 3 in the decimal 132.76 is 30
The place of 1 in the decimal 132.76 is 100.

Examples:

1. Write the place value of digit 7 in the following decimal number: 5.47?

The number 7 is in the place of hundredths, and its place value is 7 x 10 ^-2 = 7/100 = 0.07.

2. Identify the place value of the 6 in the given number: 689.87?

Given number is 689.87

The place of 6 in the decimal 689.87 is 600 or 6 hundreds.

3. Write the following numbers in the decimal place value chart.

(i) 4532.079

(ii) 490.7042

Solutions:

(i) 4532.079

4532.079 in the decimal place value chart.

example of decimal place value for the given number

(ii) 490.7042

490.7042 in the decimal place value chart.

decimal place value chart examples

HCLTECH Pivot Point Calculator

Understanding Overheads Expenses – Definition, Types, Examples | How do you Calculate Overhead Expenses?

March 18, 2024March 18, 2024 by Prasanna

Overhead expenses are business and other costs which are not related to direct materials, labor, and production. Overhead expenses are some of the indirect costs which are not related to particular business activities. Calculating the overhead expenses is not only important for budgeting but also to determine the charge or investment for a product or service. Suppose that you have a good business that is service-based. Apart from the direct investments or costs, indirect costs like insurance, rent, utilities are considered as overheads expenses.

To understand it better we will consider another example, ie., Suppose a person bought a TV at the cost price of Rs 12,000. Now, he took cable connection for the TV. He has to pay the cable bill every month which is considered as an overhead expense.

What are Overhead Expenses?

Overhead Expenses support the business but they do not generate any revenue. These expenses are mandatory and you have to pay them irrespective of your revenue. The main examples of overhead expenses are property taxes, utilities, office supplies, insurance, rent, accounting and legal expenses, advertising expenses, government licenses and fees, depreciation, and property taxes.

Types of Overhead Expenses

Among the overhead expenses, not all the expenses are the same or equal. These expenses are divided into 3 categories. Know the different expenses and their types which can create a meaningful budget for the business. The different types of overhead expenses are:

Fixed Overhead
Variable Overhead
Semi-Variable Overhead

1. Fixed Overhead Expense

These expenses are something which won’t change from month to month. If a fixed overhead has to change then it changes only annually during the renewal period. Examples of fixed overhead are insurance, salaries, rent. These overhead expenses are easy to budget and plan. These fixed overheads are tough to reduce or restrict the cash flow.

2. Variable Overhead Expense

These expenses are mostly affected by business activities and not by sales. Some of the examples of variable overhead expenses are office supplies, legal expenses, repairs, advertising expenses, and maintenance expenses. It is no guarantee that office supplies will not change according to sales volume. In the same way, advertising expenses may increase during peak sales. The drawback of variable expense is that it is difficult to predict while budgeting.

3. Semi-Variable Expenses

These expenses are also not the same from month to month. These semi-variable expenses are also not completely unpredictable and some examples of these expenses are many utilities, hourly wages, some commissions, and vehicle expenses.

Also, See:

Calculating Overhead Rate

Calculating overhead rate is an important factor in the business. It determines the exact amount of sales that goes into overhead expenses. To calculate it, we have to add all the overhead expenses and divide that number with your sales. The formula of overhead rate is:

Overhead Rate = Overhead Expenses / Sales

Overhead Charges Examples

Example 1.
An industry estimated the factory overhead for the period of 10 years at 1,60,000. The estimation of materials produced for 40,000 units is 200,000. Production requires 40,000 hours of man work at the estimated wage cost of 80,000. Machines will run for 25,000 hours approximately. Calculate the overhead rate on each of the following bases:
i. Direct labor cost
ii. Machine hours
iii. Prime Cost

Solution:

To find the direct labour cost, machine hours and prime cost we have to calculate the overhead rate.
(i) Direct Labour Cost
= (Estimated Factory OverHead / Estimated Direct Labour Cost) * 100
= (1,60,000 / 80,000) * 100
= 200%
(ii) Machine hours
= (Estimated Factory Overhead / Estimated Machine hours)
= 1,60,000 / 25,000
= 6.40 per machine hour
(iii) Prime Cost Basis
= Estimated Factory Overhead / Estimated prime cost
= 1,60,000 / (2,00,000 + 80,000)) * 100
= 89%

Example 2.
A shopkeeper purchased a second hand car for Rs. 1,40,000. He spent Rs. 15,000 on its repair and painting and then sold it for Rs. 17,000. Find his profit or loss?

Solution:
Cost Price = Rs. 1,40,000
Overhead Charges = Rs. 15,000
C.P.N = (1,40,000 + 15,000) = Rs. 1,55,000
S.P = Rs. 17,000
Therefore, S.P > C.P
Hence, it is profit
Profit Percent = S.P – C.P
P = 170000 – 155000
P = Rs. 15000
P% = P / C.P.N * 100
P% = 15000/155000 * 100
P% = 300/31%
Therefore, the profit percentage is 300/31%

Example 3.
A retailer buys a radio for Rs. 225. His overhead expenses are Rs. 15. If he sells the radio for Rs. 300. Determine his profit percentage?

Solution:
Cost Price of radio = Rs. 225
Overhead expenses = Rs. 15
Selling Price of radio = Rs. 300
Net Cost Price = Rs. 225 + 15 = 240
Profit % = Selling Price – Cost Price / Cost Price * 100
P% = 300 – 240 / 240 * 100
P% = 60/240 * 100
P% = 25%
Therefore, the profit percentage = 25%

Frequently Asked Questions on Overhead Costs

1. What are the examples of overhead expenses?

The examples of overhead expenses are interest, labor, advertising, insurance, accounting fees, travel expenditure, telephone bills, supplies, utilities, taxes, legal fees, repairs, legal fees, etc.

2. What are the types of overhead?

The types of overheads are fixed overhead expense, semi-variable overhead expense, and variable overhead expense.

3. What is the minimum percentage for overhead?

The minimal percentage is that it should not exceed 35% of the total revenue. In growing or small businesses, the overhead percentage factor is usually considered as the critical figure which is of concern.

4. How will overhead affect profit?

Overhead represents the supporting costs of production or service delivery. If there is an increase in overhead, it reduces profits by the exactly same amount.

DRREDDY Pivot Point Calculator

Worksheet on Cost Price, Selling Price and Rates of Profit and Loss | Calculating C.P, S.P, Profit and Loss Worksheets

March 2, 2024March 2, 2024 by Prasanna

Worksheet on Cost Price, Selling Price, and Rates of Profit and Loss will help the students to learn different problems on C.P., S.P., Profit, and Loss. Check out every problem available in this article and solve them to know how to solve profit and loss problems. You can crack the exams easily by solving the problems in this article. We have explained every problem along with answers.

Also, find:

Cost Price, Selling Price, and Rates of Profit and Loss Worksheet with Answers

1. A seller sells a keyboard at a price of Rs 1,500. If the cost price of the keyboard was Rs 2,500, find the profit/loss in which the shopkeeper is. Also, find the percent for the same.

Solution:

Given that a seller sells a keyboard at a price of Rs 1,500.
Selling Price = Rs 1,500
If the cost price of the keyboard was Rs 2,500,
Cost Price = Rs 2,500
Loss = Cost Price – Selling Price = Rs 2,500 – Rs 1,500 = Rs 1,000
Now, find the Loss%.
Loss Percentage = (LOSS/C. P) *100 = (1000/2500) *100 = 40%

Therefore, the loss is Rs 1,000 and the Loss% is 40%.

2. A man buys 15 TVs at a rate of Rs 12,000 per TV and sells them at a rate of Rs 13,500 per unit. Find the total profit/loss faced by the man. Also, find the percent for the same.

Solution:

Given that a man buys 15 TV at a rate of Rs 12,000 per TV.
The cost price of the TV = Rs 12,000
He sells them at a rate of Rs 13,500 per unit.
The Selling price of the TV = Rs 13,500
Since, SP>CP,
Profit = Selling price – Cost Price = Rs 13,500 – Rs 12,000 = RS 1500
Profit% = (Profit/Cost Price)*100% =(1500/12,000)*100% = 12.5%.

Therefore, the Profit = RS 1500 and Profit% = 12.5%.

3. A person bought two refrigerators at Rs 20,000 each. He sold one at a profit of 10% and the other at a loss of 10%. Find whether he made an overall profit or loss.

Solution:

The Cost price of a refrigirator = Rs 20000
profit = 10%
Selling Price = [100 + p/100] × Cost Price = [100 + 10/100] × 20000
Selling Price = 110/100 × 20000 = 11 × 2000 = Rs. 22000
Loss = 10%
Selling price = [100 – L/100] × Cost Price = [100 – 10/100] × 20000
Selling Price = 90/100 × 20000 = 9 × 2000 = Rs. 18000
Total cost price = Rs 20000 + Rs 20000 = Rs 40000
Total selling price = Rs. 22000 + Rs. 18000 = Rs 40000
Here Cost Price = Selling Price

Therefore, there no profit or no loss.

4. An owner of a Hyundai car sells his car at a price of 5,50,000 with a loss present of 10.5%. Then find the price at which he purchased the Hyundai car and also find the loss suffered by the owner.

Solution:

Given that an owner of a Hyundai car sells his car at a price of RM 5,50,000 with a loss present of 10.5%.
The Selling Price SP = Rs. 5,50,000
Loss% = 10.5
Let the Cost Price CP is X.
Now, find the Cost price.
Selling Price = Cost Price – 10.5%
Rs. 5,50,000 = X – 10.5%
Rs. 5,50,000 = X*(100 – 10.5)/100
Rs. 5,50,000 = 0.895X
X = 5,50,000/0.895
X = 614525
Loss = 614525 – 5,50,000 = 64525

Therefore, the cost of the car is 614525. The loss suffered by the owner is Rs. 64525.

5. A shop owner buys 20 television sets from a retailer at a rate of Rs 30,000 per set. He sells half of them at a profit of 25% and rests half at a loss of 20%. Find the overall profit/loss faced by the shopkeeper?

Solution:

Given that a shop owner buys 20 television sets from a retailer at a rate of Rs 30,000 per set. He sells half of them at a profit of 25% and rests half at a loss of 20%.
As he sells them at profit of 25%, (30,000 * 5 sets) * 25% = 37,500
If he sold the other half at a loss of 20%;, (30,000 * 5 sets) * 20% = 30,000

Profit (loss) = Rs. 37,500 – Rs. 30,000 = Rs. 7500

6. If the selling price of a commodity is Rs 8,000 with a profit of 15%, find the cost price of the commodity.

Solution:

Given that the selling price of a commodity is Rs 8,000.
Profit% = 15%.
The cost price of the commodity when the selling price and Profit% is
Cost price = (Selling Price × 100)/(100 + Profit percentage)
Cost price = (8000 * 100)/(100 + 15) = 80,000/115 = 6956.52

Therefore, the cost price of the commodity is Rs 6956.52.

7. If the selling price of a product is Rs 9,000 with a loss of 10%, find the cost price of the product?

Solution:

Given that the selling price of a commodity is Rs 9,000.
Loss% = 10%.
The cost price of the commodity when the selling price and Loss% is
Cost price = (Selling Price × 100)/(100 – Loss percentage)
Cost price = (9000 * 100)/(100 – 10) = 90,000/90 = 10000

Therefore, the cost price of the product is Rs 10000.

8. If a bike toy is bought at the cost price of Rs 10,000 and sold at a loss of 25%, find the selling price of the bike toy?

Solution:

Given that the cost price of a bike toy is Rs 10,000.
Loss% = 25%.
The selling price of the bike toy when the cost price and Loss% is
Selling Price = Cost Price [(100 – Loss Percentage)/100]
Selling Price = 10000 [(100 – 25)/100] = Rs 7500

Therefore, the Selling price of the bike toy is Rs 7500.

9. A ceiling fan is bought for Rs. 500 and sold for Rs. 600. Find the gain percent?

Solution:

Given that a ceiling fan is bought for Rs. 500 and sold for Rs. 600. From the given information, the cost price = Rs. 500 and Sale price = Rs. 600.
Now, find the Profit.
Profit or Gain = Selling Price – Cost Price = Rs. 600 – Rs. 500 = Rs. 100
Profit percent or gain percent = (Profit/Cost Price) x 100% = (100/600) x 100% = 16.66%

Therefore, the gain percent of the book is 16.66%.

10. A seller buys chairs from a dealer at a rate of Rs 250 per chair. He sells them at a rate of Rs 325 per chair. He buys 3 chairs of the same type and at the same rate. Find the overall profit/loss. Also profit percent/ loss percent.

Solution:

Given that a seller buys a chair from a dealer at a rate of Rs 250 per battery.
The cost price rate = Rs 250 per chair.
Total cost price = Rs 250 x 3 = Rs 750
He sells them at a rate of Rs 325 per chair.
Selling price rate = Rs 325 per chair
Total selling price = Rs 3250
He buys 3 chairs of the same type and at the same rate.
Profit = total selling price – total cost price
= Rs 3250 – Rs 750 = Rs 2500
= Rs 2500

Profit percent = (2500/750) x 100 % = 333.33%

11. A person bought some car toys at the rate of 30 for Rs. 60 and sold them at 4 for Rs. 28. Find his gain or loss percent.

Solution:

Given that a person bought some car toys at the rate of 30 for Rs. 60 and sold them at 4 for Rs. 28.
Cost price of 30 pens = Rs. 60 → Cost price (CP) of 1 pen = Rs. 2.
Selling price of 4 pens = Rs. 28 → Selling price (SP) of 1 pen = Rs. 28/4 = Rs. 7
Therefore, Gain = 7 – 2 = 5.
Gain percent = 5/2 * 100 = 250%

Therefore, the answer is 250%.

Dividend and Rate of Dividend – Definition, Formula, Examples | How to Calculate Dividend and Dividend Rate?

February 29, 2024February 29, 2024 by Prasanna

Students who are in search of the Dividend and Rate of Dividend examples can get them on this page. The profit which a shareholder gets for its investment from the organization is known as a dividend. Know what is dividend and what is rate of dividend from here. Let us discuss in detail the dividend and rate of dividend like definitions, formulas, procedures on how to calculate dividend, dividend rate, etc. So, refer to our page to improve your math skills and also to gain good marks in the exams.

Dividend and Rate of Dividend – Definitions

Dividend plays an important role in starting a business or company. The share of the annual profit of a company shared among its shareholders is known as a dividend. The rate of dividend is expressed as a percentage of the face value is called the rate of dividend.

Difference Between Dividend Rate Vs. Dividend yield

Dividend and dividend rates both are not the same. The dividend rate is the amount of share that is obtained from the shareholders such as mutual funds, stock market, etc. Whereas the dividend is the share of the profit among the shareholders.

Dividend and Rate of Dividend Formulas

Dividend Rate = Divided per share/current price
Dividend Yield = Dividend per share/ Market value per share

Refer More:

How to Calculate Dividend Rate?

The estimation of the dividend rate of a venture, asset, or portfolio includes duplicating the latest intermittent dividend installments by the number of installment periods in a single year.

Dividend and Rate of Dividend Question and Answers

Example 1.
130 shares of Rs 30 each paying 10% dividend.
Solution:
Number of shares = 130
Price of each share = 30
Therefore, total investment = Rs(30 × 130) = 1300
Dividend = 10%
Hence annual income = 10×1300/100 = 130

Example 2.
40 shares of Rs 200 each available at Rs 35 and playing 6% dividend.
Solution:
Number of shares = 50
Price of each share = 200
Face value of 40 shares = Rs( 200 × 40) = 8000
Dividend = 6%
Hence annual income = 6 × 8000/100 = 480

Example 3.
180 shares of Rs 50 each paying 15% dividend.
Solution:
Number of shares = 180
Price of each share = 50
Therefore, total investment = Rs(50 × 180) = 9000
Dividend = 15%
Hence annual income = 15×9000/100 = 1350

Example 4.
70 shares of Rs 60 each available at Rs 65 and playing 4% dividend.
Solution:
Number of shares = 50
Price of each share = 60
Face value of 70 shares = Rs( 60 × 70) = 4200
Dividend = 4%
Hence annual income = 4 × 4200/100 = 168

Example 5.
260 shares of Rs 60 each paying 2% dividend
Solution:
Number of shares = 260
Price of each share = 60
Therefore, total investment = Rs(60 × 260) = 15,600
Dividend = 2%
Hence annual income = 2×15,600/100 = 312

FAQs on Dividend and Rate of Dividend

1. What is the rate of dividend?

The dividend rate is expressed as the percentage or yield, which is a financial ratio that shows how much a company pays out in dividends each year relative to its stock price. The dividend payout ratio is one way to assess the sustainability of a company’s dividends.

2. What is the difference between dividend rate and dividend yield?

The dividend rate is another way to say dividend, which is the dollar amount of the dividend paid on a dividend-paying stock. The dividend yield is the percentage relationship between the stock’s current price and the dividend currently paid.

3. What is the dividend rate per share?

Dividend per share is the sum of declared dividends issued by a company for every ordinary share outstanding. DPS is calculated by dividing the total dividends paid out by a business, including interim dividends, over a period of time, usually a year, by the number of outstanding ordinary shares issued.

MUTHOOTFIN Pivot Point Calculator

Volume of Cuboid – Definition, Facts, Formula, Examples | How to Calculate Volume of Cuboid?

February 26, 2024February 26, 2024 by Prasanna

I think all the students of grade 9 are familiar with the solid figures. Here on this page, we will discuss in-depth the volume of cuboids like what the volume of cuboids exactly is, formulas, and how to calculate the volume of cuboids. Therefore the students who are looking forward to knowing about the volume of the cuboid can make use of our page and prepare well for the exams. In addition to this, you can find examples of the volume of the cuboid here.

What is the Volume of Cuboid?

Volume is the quantity that is used to measure solid figures like cuboids. A cuboid is a three-dimensional geometric figure. Simply we can say that a cuboid is a rectangular three-dimensional figure. In a rectangular cuboid, all the angles are right angles. A cuboid has 12 edges, 6 faces, and 8 vertices. A cuboid has three dimensions such as length, breadth, and height.
cuboid

So, we can measure the space occupied by the cuboid by using the volume formula. The units of volume of a cuboid are cubic units. The volume of a cuboid completely depends upon the length, breadth, and height of the object.

Formula of Volume of Cuboid

The unit of volume of cuboids is cubic units like cu. meter, cu. cm, cu. inches etc.
The formula of volume of cuboid is l × b × h
where,
l = length
b = breadth
h = height

Volume of Cuboid Prism | Volume of Rectangular Prism

A cuboid or rectangular prism is the same. A cuboid has six faces, eight vertices, and 12 edges. We can say that a cuboid is a solid rectangle. The top and bottom surfaces are the same in the cuboid. We can find the volume of the cuboid prism using the formula.
The volume of a rectangular prism or cuboid prism = length × breadth × height

How to find Volume of Cuboid?

We know that the volume of the cuboid can be calculated using the dimensions of the given figure. So, to find the volume of the cuboid we have to follow some steps. The scenario to calculate the volume of the cuboid is shown below.
Step 1: Check the dimensions of the given cuboid.
Step 2: Check the length, breadth, and height and see whether all the units are the same.
Step 3: If the units are not the same then convert them and make them into the same units.
Step 4: And then apply the volume of the cuboid formula.
Step 5: At last write the obtained value and write it in cubic units.

Also, Check:

Volume of Cuboid Questions

Check out the problems given below to know how to find the volume of a cuboid. If you learn these problems the students of 9th grade can solve any type of problem from the topic Volume of Cuboid.

Example 1.
Find the volume of a cuboid of dimensions 2 cm × 4 cm × 6 cm.
Solution:
Given that
cuboid_2
Length = 2 cm
Breadth = 4 cm
Height = 6 cm
We know that
The volume of cuboid = length × breadth × height.
Volume of cuboid = 2 cubic cm × 4 cubic cm × 6 cubic cm.
= 48 cubic cm.
Therefore, the volume of the cuboid = 48

Example 2.
A water tank is 10 cm long, 15 cm broad and 5 cm high. What is the volume of a water tank in cubic cm?
Solution:
Given that,
cuboid_3
The length of the water tank = 10cm
The breadth of the water tank = 15 cm
The height of the water tank = 5 cm
We know that,
The volume of cuboid = length × breadth × height.
Volume of cuboid = 10 × 15 × 5 cuboid cm
Therefore, the volume of water tank = 750

Example 3.
Kiran made a bangle box for his sister with a length of 12 cm, breadth of 34 cm, and height of 18 cm. Find the volume of the bangle box.
Solution:
Given that,
cuboid_4
Kiran made a bangle box for his sister of length = 12 cm
Kiran made a bangle box for his sister of breadth = 34 cm
Kiran made a bangle box for his sister of height = 18 cm
The volume of the bangle box = Length × breadth × height
= 12 × 34 × 18
= 7344cu cm.
Therefore, the volume of a bangle box = 7344 cu cm

Example 4.
Find the number of cubical boxes of 4 cm which can be accommodated in a carton of dimensions 24 cm × 6 cm × 8 cm.
Solution:
Given that,
Side of a box = 4
Volume of box = side × side × side.
= 4 × 4 × 4
= 64 cu. cm.
Volume of carton = length × breadth × height.
cuboid_5
= 24 × 6 × 8
=1152 cu. cm.
A number of boxes = Volume of carton/Volume of each box.
= 1152/64
Therefore, the number of cubical boxes = 18.

Example 5.
How many bricks each 15 cm long, 3 cm wide, and 7cm thick will be required for a wall 2 m long, 22 m high, and 6 m thick? If bricks sell at $600 per thousand what will it cost to build the wall?
Solution:
Given that
cuboid_6
Length of the brick = 15 cm
Width of the brick = 3 cm
Thick of the brick = 7 cm
Volume of the wall = 15 m × 3 m × 7 m
= 2 × 100 cm × 22 × 100 cm × 6 × 100 cm
= 264000000
Volume of brick = 15 cm × 3 cm × 7 cm
= 315
Number of bricks = Volume of the wall/Volume of the brick
= 200 × 2200 × 600/15 × 3 × 7
= 264000000/315
The number of bricks = 838095
The cost of 1 thousand bricks = $ 600
The cost of building the wall = $ 600 × 838095 = $ 502857000

FAQs on Volume of Cuboid

1. How do we define the volume of a cuboid?

A volume of cuboids is defined as the amount of space occupied by the cuboid surface in a three-dimensional figure.

2. If the units of dimensions of a cuboid are different, then how to find the volume?

If the units of length, width, and height are different then, we need to convert them into the same unit first and then find the volume.

3. What is the formula for the volume of cube and cuboid?

The volume of the cuboid is the product of length, width, and height.
Volume of cuboid = lbh
Volume of cube = s × s × s

Must Read:

IOC Pivot Point Calculator

Mean of Ungrouped Data – Definition, Formula, Explanation, Examples | How to Calculate Arithmetic Mean of Raw Data

February 24, 2024February 24, 2024 by Prasanna

Mean of Ungrouped Data: Ungrouped data is the type of distribution where individual data is presented in a raw form. The mean of data shows how the data are scattered throughout the central part of the distribution. Hence, the arithmetic numbers are called the measures of central tendencies.

Here, the mean is also known as the arithmetic mean or average of all the observations in the data. In this article, we will be explaining what is the mean of ungrouped data, the formula to find the mean for ungrouped data, steps to calculate mean deviation for raw data, some practice Examples on Mean of Arrayed Data.

Do Check Related Articles:

Mean of Raw Data or Arrayed Data or Ungrouped Data

In Statistics, Mean is nothing but the measurement of average and it defines the central tendency of a given set of data.

In short, the mean of the given data set is estimated by adding all the observations and then dividing by the total number of observations.

The mean of ungrouped data is denoted by the mathematical symbol or notation ie, $\overline{x}$

The mean of the ungrouped data or arrayed data when it is raw can be measured by utilizing the following formula:

The mean of n observations (variables) x₁, x₂, x₃, x₄, ….., x_n is given by the formula:

Mean = (x₁+ x₂ + x₃ + x₄ +…..+ x_{n )}/ n = ∑x_i/ n

where ∑x_i= x₁+ x₂ + x₃ + x₄ +…..+ x_n

For instance, let’s take the scores of 10 students are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50.

Hence, the mean scores of 10 students = ∑x_i/ n

= 5+10+15+20+25+30+35+40+45+50 / 10 = 27.5(approx).

Formula for Ungrouped Mean Data

Arithmetic Mean Formulas

How to Find Assumed Mean of Ungrouped Data?

Want to know more about the assumed mean of ungrouped data? Please have a look at the below stuff and understand the concept of it clearly.

In the method of assumed mean, the values that are taken from the data or not can be used as assumed mean. Yet, it must be centrally positioned in the data so that to determine the mean of the given data via easy calculations.

The formula for the Assumed mean of ungrouped data is A+ sd/N

Where, A is the assumed mean,
sd is the summation of X-A for all figures, and
N is the frequency or the number of elements in the given data.

Apply the formula directly and calculate the assumed mean of the given data with ease and confidence.

Steps to Determine the Mean Deviation for Ungrouped data

The following steps are mainly helpful for all students to calculate the mean for ungrouped data. Simply have a look at them and solve the arithmetic mean of raw data easily.

Let x₁, x₂, x₃, x₄, ….., x_n observations consist in the given set of data.

Step 1: In the first step, we have to find out the mean deviation of the measure of central tendency. Assume that the measure is a.
Step 2: Find the absolute deviation of each variable from the measure of central tendency which is obtained in step 1 ie.,
|x₁ – a|, |x₂ – a|, |x₃ – a|, …., |x_n – a|
Step 3: Estimate the mean of all absolute deviations. At last, it provides the mean absolute deviation (M.A.D) about a for ungrouped data ie.,

If the central tendency measure is mean then the resulted equation can be rewritten as:
Where, $\overline{x}$ is the mean.

Let’s understand these calculating steps very clearly by practicing with the solved mean of ungrouped data questions with answers.

Mean of Ungrouped Data Example Problems

Example 1:
In the competition of banana eating, the number of bananas consumed by 7 contestants in an hour is as follows: 10, 13, 16, 19, 22, 25, 30. Find the mean deviation from the mean of the given raw data.
Solution:
Given the number of bananas eaten by 7 contestants are 10, 13, 16, 19, 22, 25, 30
Let’s apply the above steps for finding the M.A.D about the mean.
Step 1: The mean of the following data can be given by,
$\overline{x}$ = $\frac { 10+13+16+19+22+25+30 }{ 7 } $
= $\frac { 135 }{ 7 } $ = 19.2(appox)
Step 2: Now find the absolute deviation around each observation,
|x₁ – $\overline{x}$| = |10-19| = 9
|x₂ – $\overline{x}$| = |13-19| = 6
|x₃ – $\overline{x}$| = |16-19| = 3
|x₄ – $\overline{x}$| = |19-19| = 0
|x₅ – $\overline{x}$| = |22-19| = 3
|x₆ – $\overline{x}$| = |25-19| = 6
|x₇ – $\overline{x}$| = |30-19| = 11
Step 3: Finally, calculate the mean deviation for ungrouped data by using the following formula:
M.A.D(x) = ∑ⁿ_i=1|x_i−a| / n
= $\frac { 9+6+3+0+3+6+11 }{ 7 } $
= $\frac { 38 }{ 7 } $ = 5.428

Example 2:
The mean length of ropes in 20 coils is 12 m. A new coil is added in which the length of the rope is 16 m. What is the mean length of the ropes now?
Solution:
Given that, the mean length of ropes in 20 coils is 12 m. Let’s find the sum of length for each rope using mean formula:
Mean(length) A = x₁+ x₂ + x₃ + x₄ +…..+ x₂₀/ 20
⟹ 12 = x₁+ x₂ + x₃ + x₄ +…..+ x₂₀ / 20
⟹ x₁+ x₂ + x₃ + x₄ +…..+ x_n = 240 …….(i)
Now, add one coil and find the mean of new coils of rope,
A = x₁+ x₂ + x₃ + x₄ +…..+ x₂₀ + x₂₁/ 21
Here, length of new rope is 16m and use equation (i)
= x₁+ x₂ + x₃ + x₄ +…..+ x₂₀ + x₂₁/ 21
= $\frac { 240 + 16}{ 21 } $
= $\frac { 256 }{ 21 } $
= 12.19 (Appox)
Hence, the required new mean length is 12.19 m approximately.

Example 3:
The ages in years of 6 teachers of a school are 32, 28, 54, 40, 65, 20. What is the mean age of these teachers?
Solution:
Mean age of the teachers = $\frac { Sum of the age of teachers}{ Number of teachers } $
= $\frac { (32+28+54+40+65+20) }{ 6 } $
= $\frac { 239 }{ 6 } $
= 39.8 (approx) years.

BODMAS/PEMDAS Rules – Involving Decimals | Order of Operations with Decimals Questions and Answers

February 23, 2024February 23, 2024 by Prasanna

We can easily simplify the arithmetic expression which involves decimals by using the BODMAS Rules or PEMDAS Rules. Some children will get confused while simplifying an arithmetic expression but by using the BODMAS rule, they can simply solve the expressions. Check out the Order of Operations and solved examples of BODMAS Rules Involving Decimals in this article. We have clearly given questions and answers along with the explanations for your best practice.

Also, Check:

Order of Operations Involving Decimals Questions and Answers

Example 1.

First priority for Bracket terms: Solve inside the Brackets/parenthesis before Of, Multiply, Divide, Add or Subtract.
For example 1.2 + (1.5 – 2.3).

Solution:

The given expression is 1.2 + (1.5 – 2.3).
1.2 + (1.5 – 2.3) = 1.2 + (- 0.8) (subtraction of bracket term).
= 1.2 – 0.8.
= 0.4.
Finally, 1.2 + (1. 5 – 2. 3) is equal to 0.4.

Example 2.

Order terms are second priority: Then, solve Of part (Exponent, Powers, Roots, etc.,) before Multiply, Divide, Add or Subtract.
For example 0.2 X (1.2 + 1.4) + (0.2)^2.
Solution:

The given expression is 0.2 X (1.2 + 1.4) + (0.2)^2.
0.2 X (1.2 + 1.4) + (0.2)^2 = 0.2 X 2.6 + (0.2)^2 ( bracket terms addition first).
= 0.2 X 2.6 + 0.04 (order term (0.2)^2 = 0.04).
= 0.52 + 0.04 (multiplication 0.2 X 2.6 = 0.52).
= 0.56 (addition 0.52 + 0.04 = 0.56).
Therefore, 0.2 X (1.2 + 1.4) + (0.2)^2 is equal to 0.56.

Example 3.

Division and Multiplication: Then, calculate Multiply or Divide before Add or Subtract start from left to right.
For example 1.4 + 1.6 ÷ 0.2 X 0.2.
Solution:

The given expression is1.4 + 1.6 ÷ 0.2 X 0.2.
1.4 + 1.6 ÷ 0.2 X 0.2 = 1.4 + 8 X 0.2 (division 1.6 ÷ 0.2 = 8).
= 1.4 + 0.4 (multiplication 8 X 0.2 = 0.4).
= 1.8 (addition 1.4 + 0.4 = 1.8).
Therefore, 1.4 + 1.6 ÷ 0.2 X 0.2 is equal to 1.8.

Example 4.

Addition and Subtraction: At last Add or Subtract start from left to right.
For example 1.5 + (3.2 – 1.6) + 0.1.
Solution:

The given expression is 1.5 + (3.2 – 1.6) + 0.1.
1.5 + (3.2 – 1.6) + 0.1 = 1.5 + 1.6 + 0.1 (subtraction of bracket terms 3.2 – 1.6 = 1.6).
= 3.2 (addition 1.5 + 1.6 + 0.1 = 3.2).
Therefore, 1.5 + (3.2 – 1.6) + 0.1 is equal to 3.2.

BODMAS Rules Involving Decimals Questions and Answers

Problem 1.

Simplify the below expressions by using the BODMAS rules.
(i) 0.4 + 0.8 ÷ 0.2 + 0.2 X 0.4.
(ii) 0.2 X 0.5(1.2 + 2.1) + 2.5.
(iii) 0.6 – 0.2 X 1.2 + 1.6.
(iv) 1.2 + [2.5 + (2.6 – 1.6) – 2.4)] – 3.2.
(v) 0.8 + 1.2 X 0.5 + 1.2.

Solution:

(i) 0.4 + 0.8 ÷ 0.2 + 0.2 X 0.4.
Solution:
The given expression is 0.4 + 0.8 ÷ 0.2 + 0.2 X 0.4.
0.4 + 0.8 ÷ 0.2 + 0.2 X 0.4 = 0.4 + 4 + 0.2 X 0.4 (division 0.8 ÷ 0.2 = 4).
= 0.4 + 4 + 0.08 (multiplication 0.2 X 0.4 = 0.08).
= 4.48.
By using the BODMAS Rule, 0.4 + 0.8 ÷ 0.2 + 0.2 X 0.4 is equal to 4.48.

(ii) 0.2 X 0.5(1.2 + 2.1) + 2.5.
Solution:
The given expression is 0.2 X 0.5(1.2 + 2.1) + 2.5.
0.2 X 0.5(1.2 + 2.1) + 2.5 = 0.2 X 0.5(3.3) + 2.5 (addition 1.2 + 2.1 = 3.3).
= 0.2 X 0.5 X 3.3 + 2.5
= 0.33 + 2.5 (multiplication 0.2 X 0.5 X 3.3 = 0.33).
= 2.83 (addition 0.33 + 2.5 = 4.83).
By using the BODMAS rule, the given expression 0.2 X 0.5(1.2 + 2.1) + 2.5 is simplified as 2.83.

(iii) 0.6 – 0.2 X 1.2 + 1.6.
Solution:
The given expression is0.6 – 0.2 X 1.2 + 1.6.
0.6 – 0.2 X 1.2 + 1.6 = 0.6 – 0.24 + 1.6 (multiplication 0.2 X 1.2 = 0.24).
= 2.2 – 0.24 (addition 0.6 + 1.6 = 2.2).
= 1.96 (subtraction 2.2 – 0.24 = 1.96).
Finally, by using the BODMAS rule, the given expression 0.6 – 0.2 X 1.2 + 1.6 is simplified as 1.96.

(iv) 1.2 + [2.5 + (2.6 – 1.6) – 2.4)] – 3.2.
Solution:
The given expression is 1.2 + [2.5 + (2.6 – 1.6) – 2.4)] – 3.2.
1.2 + [2.5 + (2.6 – 1.6) – 2.4)] – 3.2 = 1.2 + [2.5 + (1.0) – 2.4)] – 3.2 (subtraction in brackets 2.6 – 1.6 = 1.0).
1.2 + [2.5 + (2.6 – 1.6) – 2.4)] – 3.2 = 1.2 + [3.5 – 2.4] – 3.2 (addition 2.5 + 1.0 = 3.5).
1.2 + [2.5 + (2.6 – 1.6) – 2.4)] – 3.2 = 1.2 + 1.1 – 3.2 (subtraction 3.5 – 2.4 = 1.1).
1.2 + [2.5 + (2.6 – 1.6) – 2.4)] – 3.2 = 2.3 – 3.2 (addition 1.2 + 1.1 = 2.3).
= – 0.9 (subtraction 2.3 – 3.2 = – 0.9).
By using the BODMAS rule, the given expression 1.2 + [2.5 + (2.6 – 1.6) – 2.4)] – 3.2 is simplified as – 0.9.

(v) 0.8 + 1.2 X 0.5 + 1.2.
Solution:
The given expression is 0.8 + 1.2 X 0.5 + 1.2.
0.8 + 1.2 X 0.5 + 1.2 = 0.8 + 0.6 + 1.2 (multiplication first 1.2 X 0.5 = 0.6).
= 2.6 (addition 0.8 + 0.6 + 1.2 = 1.4 + 1.2 = 2.6).
By using the BODMAS rule, 0.8 + 1.2 X 0.5 + 1.2 is simplified as 2.6.

Must Read:

HINDALCO Pivot Point Calculator

Calculating Profit Percent and Loss Percent | Profit and Loss Problems and Solutions

February 8, 2024February 8, 2024 by Prasanna

The profit and loss are the basic components of the income statement that summarizes the revenues, costs, and expenses subjected during a certain period. We use basic concepts in the calculation of profit percentage and loss percentage. Find Formulas for Calculating Profit % and Loss % and Problems on the Same in the forthcoming modules.

Cost Price (CP)

The price at which we purchase an item is called the cost price. In short, it is written as CP.

Example: A merchant bought an item at a cost of Rs. 150 and gain a profit of Rs. 30.

In the above example, Rs.150 is the cost price.

Selling Price (SP)

The price at which we sell an item is called the selling price. In short, it is written as SP.

Example: A shop keeper purchased a pen at Rs. 40 and he sold it at Rs.50 to a customer.

In the above example Rs. 50 is the selling price.

Profit or Gain

If the selling price of an item is more than the cost price of the same item, then it is said to be gain (or) profit i.e. S.P. > C.P.

Net profit= S.P. – C.P.

Loss

If the selling price of an item is less than the cost price of the same item, then it is said to be a loss i.e. S.P. < C.P.

Net loss= C.P. – S.P.

NOTE:

It is important to note that the profit or loss is always calculated based on the cost price of an item.

Profit and Loss Formulas for Calculating Profit % and Loss%

Have a glance at the Profit and Loss Formulas for finding the Profit and Loss Percentage. They are along the lines

Net Gain = (S.P.) – (C.P.)
Net Loss = (C.P.) – (S.P.)
Gain % = (S.P. – C.P./C.P. *100)% = (gain/C.P. *100)%
Loss % = (C.P. – S.P./C.P. *100)% = (loss/C.P. * 100)%
To find S.P. when C.P. and gain% or loss% are given :
- P. = [(100 + Gain %) /100] * C.P.
- P. = [(100 – Loss %) /100] * C.P.

To find C.P. when S.P. and gain% or loss% are given :
- P. = [(100 + Gain %) /100] * S.P.
- P. = [(100 – Loss %) /100] * S.P.

Profit and Loss Percent Questions and Answers

Question 1:

A man buys a book for Rs. 60 and sells it for Rs. 90. Find his gain/loss percentage?

Solution:

By seeing the question we can understand that the Selling price of the book is more than its cost price, therefore the man has profited on his total transaction.

Given data:

Cost price (C.P.) = Rs.60

Selling price (S.P.) =Rs. 90

Net profit = S.P. – C.P.

= 90 – 60

= 30

Profit % = ((Net profit)/C.P. *100)

= (30/60 *100)

= 50%

The total gain percentage is 50%.

Question 2:

If a fruit vendor purchases 9 oranges for Rs.8 and sells 8 oranges for Rs. 9. How much profit or loss percentage does he makes?

Solution:

By seeing the question we can understand that he bought 9 oranges at cost prices Rs.8 and sells 8 oranges at Rs. 9.

Given data:

Buying 9 oranges at Rs. 8

And Selling 8 oranges at Rs. 9

Here we are making quantities equal by multiplying the prices on both sides

We get,

Quantity Price

Buying 9 * 8 8 * 8

Selling 8 * 9 9 * 9

By calculating,

Quantity Price

Buying 72 64

Selling 72 81

By observing the above calculation we can see that the vendor bought 72 oranges for Rs. 64 while he sold 72 oranges at Rs. 81. This shows that the vendor is having profit in the entire transaction.

Profit percentage = ((S.P. – C.P.)/C.P. * 100)

= ((81-64)/64 * 100)

= 26.56 %

The total gain percentage for fruit vendors selling oranges is 26.56%.

Must Read:

Nr7

Examples on Calculating Profit or Loss | Profit and Loss Questions and Answers

January 19, 2024January 19, 2024 by Prasanna

Looking for help on finding Profit and Loss Concepts? Then, you have come the right way. Here let us observe some fully solved example problems on calculating profit or loss. You can find step by step solutions to all the Profit and Loss Questions available here. Try Practicing from the Profit and Loss Problems and get acquainted with the concepts better. Learn various methods for Calculating Profit and Loss and solve related problems easily. Assess your preparation standards on the concept and concentrate on the areas you are lagging in accordingly.

Question 1:
If a manufacturer allows 40% commission on the retail price of his product, he earns a profit of 9%. What would be his profit percent if the commission is reduced by 25 percent?

Solution:

We need to find out the profit % when the given commission is reduced by 25 percent.
Given data:
According to the question consider
Cost price (C.P.) of the product = $ 100
Then, a commission of the product = $ 40
Therefore selling price (S.P.) = $ (cost price (C.P.) – commission)
= $ (100 – 40)
= $ 60
Given that profit = 9%
Therefore Cost price (C.P.) = $\frac { 100 }{ 100+gain%} $* S.P
So,
C.P. = $ $\frac { 100 }{ 100+9 } $* 60
= $ $\frac { 6000 }{109 } $
Now new commission = $ 15
Therefore new selling price (S.P.) = $ 100 – 15
= $ 75
Gain = S.P. – C.P.
= $ (75 – $\frac { 6000 }{109 } $)
= $ $\frac { 2175 }{109 } $
Gain% = ($\frac { Profit }{C.P. } $*100)%

=($\frac { 2175 }{109 } $*$\frac { 109 }{6000 } $*100)%

= 36.25 %
Hence, gain % is 36.25.
Question 2:
After getting two successive discounts, a pant with the least price of $ 200 is available at $ 125. If the second discount is 14%, find the first discount.

Solution:
Let the first discount be ‘P%’
Then, 86% of (100 – P) % of 200 = 125

$\frac { 86 }{ 100 } $*$\frac { (100 – P) }{ 100 } $*200 = 125

100-P = $\frac {(125*100*100) }{ 200*86 } $
100 – P = 72.67
P = 100 – 72.67
P = 27.32%
Therefore, first discount price of pant is 27.32%.
Question 3:
A women sells an article at a profit of 20%. If he had bought it at 15% less and sold it for $ 11.50 less, he would have gained 25%. Find the cost price of the article.

Solution:
Given data:
Consider cost price (C.P.) of article be ‘X’
First selling price of article ‘X’ = 120% of ‘X’

= $\frac { 120 }{ 100 } $*X
= $\frac { 6 }{ 5 } $*X
Cost price of article for ‘X’ at 75% = 75% of ‘X’
=$\frac { 75 }{ 100 } $*X

=$\frac { 3 }{ 4 } $*X
Second selling price of article ‘X’ = 125% of 3/4 * X
= $\frac { 125 }{ 100 } $*$\frac { 3x }{ 4 } $

= $\frac { 15x }{ 16 } $

As given the article is sold at $ 11.50 less
Therefore, selling prices are equalized to a reduced price

$\frac { 6x }{5 } $ –$\frac { 15x }{ 16 } $ = 11.50
$\frac { 21x }{80 } $ = 11.50
X = $ 43.8
Almost equal to $ 44
Hence, the cost price of an article is given as $ 44.
Question 4:
A dealer sold three – fourth of his articles at a gain of 25% and the remaining at cost price. Find the profit earned by him in the whole transaction.

Solution:
A dealer sold his ¾ th quantity with a gain of 25% and the remaining ¼ that its cost price.
Given data:
Consider cost price (C.P.) of whole articles be ‘X’
Cost price (C.P.) of $\frac { 3}{ 4} $th quantity = $ $\frac { 3x}{ 4} $
Cost price (C.P.) of $\frac { 1}{ 4} $th quantity = $ $\frac { x}{ 4} $
Total selling price (S.P.) = $ ((125% of $\frac { 3x}{ 4} $) + $\frac { x}{ 4} $)
= $ ($\frac { 15x}{ 16} $ + $\frac { x}{ 4} $)
= $ ($\frac { 19x}{ 16} $)
Profit / Gain = S.P. – C.P.
= $ ($\frac { 19x}{ 16} $ – x)
= $ $\frac { 3x}{ 16} $.
Gain % = ($\frac { gain}{ C.P. } $*100)%

= ($\frac {3x}{ 16 } $*$\frac {1}{ x } $*100)%

= 18.75%.
Hence, the gain % of the article is 18.75%.
Question 5:
A man sold two flats for $ 775,000 each. On one he gains 18% while on the other he losses 18%. How much does he gain or lose in the whole transaction?

Solution:
In this problem he gets an equal amount of profit and loss such cases there is always a loss. Therefore the selling price (S.P.) is immaterial.
Loss % = ($\frac {common loss and gain %}{ 10 } $)²

= ($\frac {18 }{ 10 } $)²

= ($\frac {324 }{ 100 } $)

= 3.24%
The total loss incurred by the person is 3.24%.
Question 6:
Pure petrol costs $ 100 per lit. After adulterating it with kerosene costing $ 50 per lit, a shopkeeper sells the mixture at the rate of $ 96 per lit, thereby making a profit of 20%. In what ratio does he mix the two?

Solution:
Here, we have two different cost prices for different mixtures and one selling price (S.P.).
Given data:
Cost price (C.P.) of petrol = $ 100 per lit
Cost price (C.P.) of kerosene = $ 50 per lit
Selling price (S.P.) of mixture = $ 96 per lit
As we have two cost prices,
Mean cost price = $($\frac {100 }{ 120 } $)* 96)

= $ 80 per lit.
Since they asked us to find a ratio it is easy to find out by the allegation rule
Cost price (C.P.) of a unit Cost price (C.P.) of a unit quantity of $ X item quantity of $ Y item
Mean cost
$ M
(M – Y) (X – M)
Similarly using this concept here,
Cost price (C.P.) of a unit Cost price (C.P.) of a unit quantity of $ 100 item quantity of $ 50 item
Mean cost
$ 80
(80 – 50) (100 – 80)
Therefore, required ratio = 30 : 20
= 3 : 2.

Question 7:
Find cost price (C.P.), when
1. Selling price (S.P.) = $ 50, Gain = 18%
2. Selling price (S.P.) = $ 51, Loss = 14%

Solution:
Here, we need to find cost price (C.P.) using below formulae
1. Given data
Selling price (S.P.) = $ 50 & Gain = 18%
C.P. = $\frac { 100 + Gain%) }{ 100 } $*S.P.

=$ $\frac { 100 + 18 }{ 100 } $*50= $ 59.
2. Given data
Selling price (S.P.) = $ 51, Loss = 14%

C.P. = $\frac { 100 – Loss% }{ 100 } $*S.P.

= $ $\frac { 100 – 14 }{ 100 } $*51

= $ 43.86.

IDEA Pivot Point Calculator

Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem

January 3, 2024January 3, 2024 by Prasanna

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem$

One has to learn the concepts if he/she wants to become a master in maths. The fundamentals in Go Math Grade 8 Answer Key Chapter 12 The Pythagorean theorem will help you to learn the subject. You need to practice from the beginning itself. We will help you to achieve your dreams by providing simple methods to solve the problems in an easy manner. Download Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem free pdf to help you to gain a grip over the subject.

Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem

Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem will help you to complete your homework in time without any mistakes. The main aim of the ccssanswers.com site is to provide quick and simple methods to all the students of 8th grade. The solutions to all the questions in Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem are prepared by the math experts. Tap the links and practice the problems provided in the HMH Go Math 8th Grade Solution Key Chapter 12 The Pythagorean Theorem.

Chapter 12- Lesson 1:

Guided Practice – The Pythagorean Theorem – Page No. 378
12.1 Independent Practice – The Pythagorean Theorem – Page No. 379
FOCUS ON HIGHER ORDER THINKING – The Pythagorean Theorem – Page No. 380

Chapter 12- Lesson 2:

Guided Practice – Converse of the Pythagorean Theorem – Page No. 384
12.2 Independent Practice – Converse of the Pythagorean Theorem – Page No. 385
Converse of the Pythagorean Theorem – Page No. 386

Chapter 12- Lesson 3:

Guided Practice – Distance Between Two Points – Page No. 390
12.3 Independent Practice – Distance Between Two Points – Page No. 391
Distance Between Two Points – Page No. 392
Ready to Go On? – Model Quiz – Page No. 393
Selected Response – Mixed Review – Page No. 394

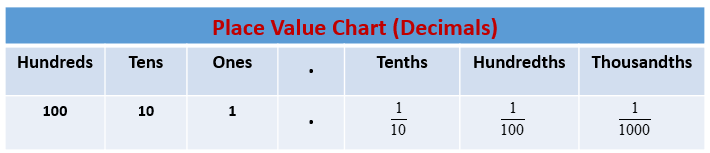
Guided Practice – The Pythagorean Theorem – Page No. 378

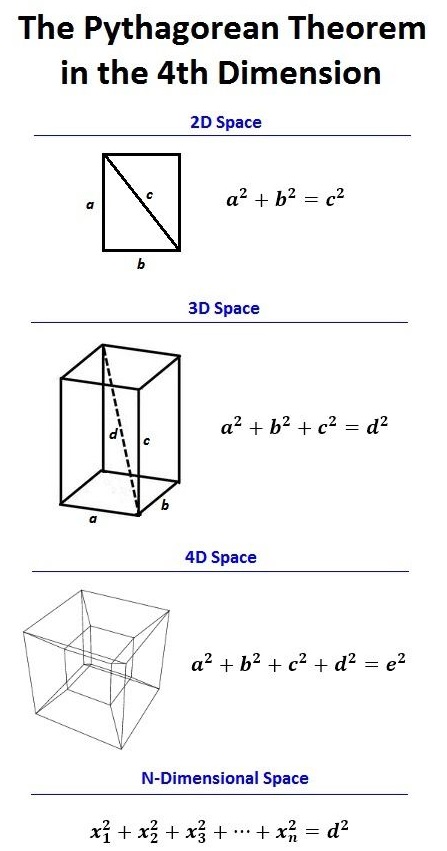
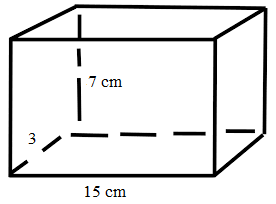
Question 1.
Find the length of the missing side of the triangle
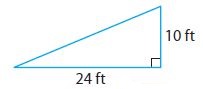
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 1: The Pythagorean Theorem img 1$
a² + b² = c² → 24² + ? = c² → ? = c²
The length of the hypotenuse is _____ feet.
_____ feet

Answer: The length of the hypotenuse is 26 feet.

Explanation: According to Pythagorean Theorem, we shall consider values of a = 24ft, b = 10ft.
Therefore c = √(a² +b²)
c = √(24²+ 10²)
= √(576 + 100)
= √676 = 26ft

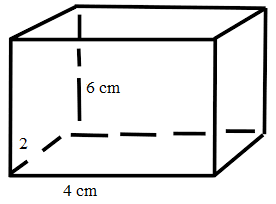
Question 2.
Mr. Woo wants to ship a fishing rod that is 42 inches long to his son. He has a box with the dimensions shown.
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 1: The Pythagorean Theorem img 2$
a. Find the square of the length of the diagonal across the bottom of the box.
________ inches

Answer: 1700 inches.

Explanation: Here we consider the length of the diagonal across the bottom of the box as d.
Therefore, according to Pythagorean Theorem
W²+ l²= d²40²+ 10² = d²1600 + 100 = d²
1700 = d²

Question 2.
b. Find the length from a bottom corner to the opposite top corner to the nearest tenth. Will the fishing rod fit?
________ inches

Answer: 42.42 inches.

Explanation: We denote by r, the length from the bottom corner to the opposite top corner. We use our Pythagorean formula to find r.
h²+ s²= r²
10²+ 1700 = r²100 + 1700 = r²1800 = r², r = √1800 => 42.42 inches

ESSENTIAL QUESTION CHECK-IN

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 378 Q3$

12.1 Independent Practice – The Pythagorean Theorem – Page No. 379

Find the length of the missing side of each triangle. Round your answers to the nearest tenth.

Question 4.
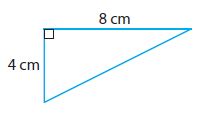
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 1: The Pythagorean Theorem img 3$
________ cm

Answer: 8.9 cm.

Explanation: According to Pythagorean theorem we consider values of a = 4cm, b = 8cm.
c²= a² + b²
= 4² + 8²= 16 + 64
c²= 80, c= √80 => 8.944
After rounding to nearest tenth value c= 8.9cm

Question 5.
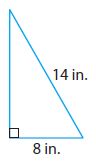
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 1: The Pythagorean Theorem img 4$
________ in.

Answer: 11.5 in.

Explanation: According to Pythagorean theorem we consider values of b = 8in, c= 14in
c²= a² + b²14²= a² + 8²
196 = a² + 64
a² = 196 – 64
a = √132 => 11.4891
a = 11.5 in

Question 6.
The diagonal of a rectangular big-screen TV screen measures 152 cm. The length measures 132 cm. What is the height of the screen?
________ cm

Answer: 75.4 cm

Explanation: Let’s consider the diagonal of the TV screen as C = 152cm, length as A = 132 cm, and height of the screen as B.

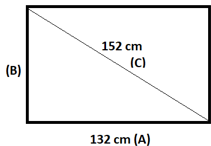
As C²= A² + B² 152²= 132²+ B²
23,104 = 17,424 + B²
B² = 23,104 – 17,424
B = √5680 => 75.365
So the height of the screen B = 75.4cm

Question 7.
Dylan has a square piece of metal that measures 10 inches on each side. He cuts the metal along the diagonal, forming two right triangles. What is the length of the hypotenuse of each right triangle to the nearest tenth of an inch?
________ in.

Answer: 14.1in.

Explanation:

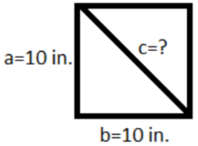
Using the Pythagorean Theorem, we have:
a²+ b² = c²
10²+ 10²= c²
100 + 100 = c²
200 = c²We are told to round the length of the hypotenuse of each right triangle to the nearest tenth of an inch, therefore: c = 14.1in

Question 8.
Represent Real-World Problems A painter has a 24-foot ladder that he is using to paint a house. For safety reasons, the ladder must be placed at least 8 feet from the base of the side of the house. To the nearest tenth of a foot, how high can the ladder safely reach?
________ ft

Answer: 22.6 ft.

Explanation: Consider the below diagram. Length of the ladder C = 24ft, placed at a distance from the base B = 8ft, let the safest height be A.

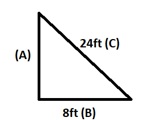
By using Pythagorean Theorem:
C² = A²+ B²
24²= A² + 8²
576 = A²+ 64
A²= 576 – 64 => 512
A = √512 => 22.627
After rounding to nearest tenth, value of A = 22.6ft

Question 9.
What is the longest flagpole (in whole feet) that could be shipped in a box that measures 2 ft by 2 ft by 12 ft?
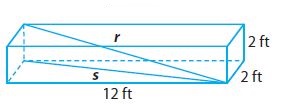
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 1: The Pythagorean Theorem img 5$
________ ft

Answer: The longest flagpole (in whole feet) that could be shipped in this box is 12 feet.

Explanation: From the above diagram we have to find the value of r, which gives us the length longest flagpole that could be shipped in the box. Where width w = 2ft, height h = 2ft and length l = 12ft.

First find s, the length of the diagonal across the bottom of the box.
w²+ l²= s²
2²+ 12²= s²
4 + 144 = s²148 = s²We use our expression for s to find r, since triangle with sides s, r, and h also form a right-angle triangle.
h²+ s²= r²
2²+ 148 = r²
4 + 148 = r²152 = r²r = 12.33ft.

Question 10.
Sports American football fields measure 100 yards long between the end zones, and are 53 $\frac{1}{3}$ yards wide. Is the length of the diagonal across this field more or less than 120 yards? Explain.
____________

Answer: The diagonal across this field is less than 120 yards.

Explanation: From the above details we will get a diagram as shown below.
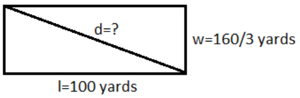
Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem

We are given l = 100 and w = 53 = . If we denote with d the diagonal of the field, using the Pythagorean Theorem, we have:
l²+ w²= d²
100²+ (160/3)²= d²10000 + (25600/9) = d²
9*10000 + 9*(25600/9) = 9* d²
90000 + 25600 = 9 d²
(115600/9) = d²
(340/9) = d²
d = 113.3
Hence the diagonal across this field is less than 120 yards.

Question 11.
Justify Reasoning A tree struck by lightning broke at a point 12 ft above the ground as shown. What was the height of the tree to the nearest tenth of a foot? Explain your reasoning.
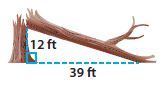
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 1: The Pythagorean Theorem img 6$
________ ft

Answer: The total height of the tree was 52.8ft

Explanation:

By using the Pythagorean Theorem
a²+ b²= c²12²+ 39²= c²
144 + 1521 = c²
1665 = c²We are told to round the length of the hypotenuse to the nearest tenth of a foot, therefore: c = 40.8ft.
Therefore, the total height of the tree was:
height = a+c
height = 12 +40.8
height = 52.8 feet

FOCUS ON HIGHER ORDER THINKING – The Pythagorean Theorem – Page No. 380

Question 12.
Multistep Main Street and Washington Avenue meet at a right angle. A large park begins at this corner. Joe’s school lies at the opposite corner of the park. Usually, Joe walks 1.2 miles along Main Street and then 0.9 miles up Washington Avenue to get to school. Today he walked in a straight path across the park and returned home along the same path. What is the difference in distance between the two round trips? Explain.
________ mi

Answer: Joe walks 1.2 miles less if he follows the straight path across the park.

Explanation: Using the Pythagorean Theorem, we find the distance from his home to school following the straight path across the park:
a²+ b²= c²1.2²+ 0.9²= c²
1.44 + 0.81 = c²
2.25 = c²
1.5 = c
Therefore, the distance of Joe’s round trip following the path across the park is 3 miles (d_home-school+ d_school-home = 1.5 + 1.5). Usually, when he walks along Main Street and Washington Avenue, the distance of his round trip is 4.2 miles (d_home-school+ d_school-home = (1.2 + 0.9) + (0.9+1.2)). As we can see, Joe walks 1.2 miles less if he follows the straight path across the park.

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 380 Q13$

Question 14.
Persevere in Problem-Solving A square hamburger is centered on a circular bun. Both the bun and the burger have an area of 16 square inches.
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 1: The Pythagorean Theorem img 7$
a. How far, to the nearest hundredth of an inch, does each corner of the burger stick out from the bun? Explain.
________ in

Answer: Each corner of the burger sticks out 0.57 inches from the bun.

Explanation: Frist, we need to find the radius r of the circular bun. We know that its area A is 16 square inches, therefore:

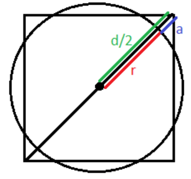
A = πr²16 = 3.14*r²r²= (16/3.14)
r = 2.26

Then, we need to find the sides of the square hamburger. We know that its area A is 16 square inches, therefore:
A = s²
16 = s²
s = 4
Using the Pythagorean Theorem, we have to find the diagonal d of the square hamburger:
s²+ s² = d²
4² + 4²= d²
16 + 16 = d²
32 = d²d = 5.66
To find how far each corner of the burger sticks out from the bun, we denote this length by a and we get:
a = (d/2) – r => (5.66/2) – 2.26
a = 0.57.
Therefore, Each corner of the burger sticks out 0.57 inches from the bun.

Question 14.
b. How far does each bun stick out from the center of each side of the burger?
________ in

Answer: Each bun sticks out 0.26 inches from the center of each side of the burger.

Explanation:

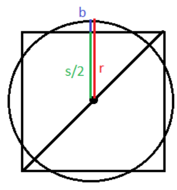
We found that r = 2.26 and s = 4. To find how far does each bun stick out from the center of each side of the burger, we denote this length by b and we get:
b = r – (s/2) = 2.26 – (4/2)
b = 0.26 inches.

Question 14.
c. Are the distances in part a and part b equal? If not, which sticks out more, the burger or the bun? Explain.

Answer: The distances a and b are not equal. From the calculations, we found that the burger sticks out more than the bun.

Guided Practice – Converse of the Pythagorean Theorem – Page No. 384

Question 1.
Lashandra used grid paper to construct the triangle shown.
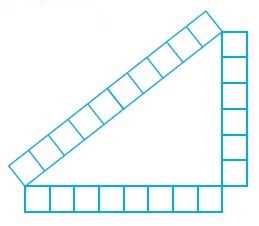
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 2: Converse of the Pythagorean Theorem img 8$
a. What are the lengths of the sides of Lashandra’s triangle?
_______ units, _______ units, _______ units,

Answer: The length of Lashandra’s triangle is 8 units, 6 units, 10 units.

Question 1.
b. Use the converse of the Pythagorean Theorem to determine whether the triangle is a right triangle.
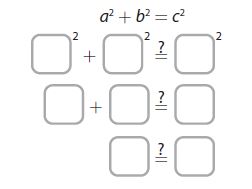
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 2: Converse of the Pythagorean Theorem img 9$
The triangle that Lashandra constructed is/is not a right triangle.
_______ a right triangle

Answer: Lashandra’s triangle is right angled triangle as it satisfied the Pythagorean theorem

Explanation:
Verifying with Pythagorean formula a²+ b²= c²8^{2 +}6²= 10²64 + 36 =100
100 = 100.

Question 2.
A triangle has side lengths 9 cm, 12 cm, and 16 cm. Tell whether the triangle is a right triangle.
Let a = _____, b = _____, and c = ______.
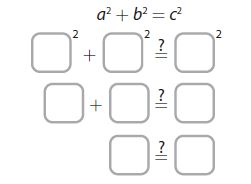
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 2: Converse of the Pythagorean Theorem img 10$
By the converse of the Pythagorean Theorem, the triangle is/is not a right triangle.
_______ a right triangle

Answer: The given triangle is not a right-angled triangle

Explanation: Verifying with Pythagorean formula a²+ b²= c²
9²+ 12²= 16²81 + 144 = 256
225 ≠ 256.
Hence given dimensions are not from the right-angled triangle.

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 384 Q3$

ESSENTIAL QUESTION CHECK-IN

Question 4.
How can you use the converse of the Pythagorean Theorem to tell if a triangle is a right triangle?
Answer:
Knowing the side lengths, we substitute them in the formula a²+ b²= c², where c contains the biggest value.
If the equation holds true, then the given triangle is a right triangle. Otherwise, it is not a right triangle.

12.2 Independent Practice – Converse of the Pythagorean Theorem – Page No. 385

Tell whether each triangle with the given side lengths is a right triangle.

Question 5.
11 cm, 60 cm, 61 cm
______________

Answer: Since 11²+ 60²= 61², the triangle is a right-angled triangle.

Explanation: Let a = 11, b = 60 and c= 61
Using the converse of the Pythagorean Theorem a²+ b²= c²11²+ 60²= 61²121 + 3600 = 3721
3721 = 3721.
Since 11²+ 60²= 61², the triangle is a right-angled triangle.

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 385 Q6$

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 385 Q7$

Question 8.
15 m, 36 m, 39 m
______________

Answer: Since 15²+ 36²= 39², the triangle is a right-angled triangle.

Explanation: Let a = 15, b = 36 and c= 39
Using the converse of the Pythagorean Theorem a²+ b²= c²15²+ 36²= 39²225 + 1296 = 1521
1521 = 1521.
Since 15²+ 36²= 39², the triangle is a right-angled triangle.

Question 9.
20 mm, 30 mm, 40 mm
______________

Answer: Since 20²+ 30²≠ 40², the triangle is not a right-angled triangle.

Explanation: Let a = 20, b = 30 and c= 40
Using the converse of the Pythagorean Theorem a²+ b²= c²20²+ 30²= 40²400 + 900 = 1600
1300 ≠ 1600.
Since 20²+ 30²≠ 40², the triangle is not a right-angled triangle.

Question 10.
20 cm, 48 cm, 52 cm
______________

Answer: Since 20²+ 48²= 52², the triangle is a right-angled triangle.

Explanation: Let a = 20, b = 48 and c= 52
Using the converse of the Pythagorean Theorem a²+ b²= c²20²+ 48²= 52²400 + 2304 = 2704
2704 = 2704.
Since 20²+ 48²= 52², the triangle is a right-angled triangle.

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 385 Q11$

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 385 Q12$

Question 13.
35 in., 45 in., 55 in.
______________

Answer: Since 35²+ 45²≠ 55², the triangle is not a right-angled triangle.

Explanation: Let a = 35, b = 45 and c= 55
Using the converse of the Pythagorean Theorem a²+ b²= c²35²+ 45²= 55²1225 + 2025 = 3025
3250 ≠ 3025.
Since 35²+ 45²≠ 55², the triangle is not a right-angled triangle.

Question 14.
25 cm, 14 cm, 23 cm
______________

Answer: Since 14²+ 23²≠ 25², the triangle is not a right-angled triangle.

Explanation: Let a = 14, b = 23 and c= 25 (longest side)
Using the converse of the Pythagorean Theorem a²+ b²= c²14²+ 23²= 25²196 + 529 = 625
725 ≠ 625.
Since 14²+ 23²≠25², the triangle is not a right-angled triangle.

Question 15.
The emblem on a college banner consists of the face of a tiger inside a triangle. The lengths of the sides of the triangle are 13 cm, 14 cm, and 15 cm. Is the triangle a right triangle? Explain.
________

Answer: Since 13²+ 14²≠ 15², the triangle is not a right-angled triangle.

Explanation: Let a = 13, b = 14 and c= 15
Using the converse of the Pythagorean Theorem a²+ b²= c²13²+ 14²= 15²169 + 196 = 225
365 ≠ 225.
Since 13²+ 14²≠ 15², the triangle is not a right-angled triangle.

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 385 Q16$

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 385 Q17$

Question 18.
History In ancient Egypt, surveyors made right angles by stretching a rope with evenly spaced knots as shown. Explain why the rope forms a right angle.
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 2: Converse of the Pythagorean Theorem img 11$

Answer: The rope has formed a right-angled triangle because the length of its sides follows Pythagorean Theorem.

Explanation: The knots are evenly placed at equal distances
The lengths in terms of knots are a=4 knots, b = 3knots, c = 5 knots
Therefore a²+ b²= c²4²+ 3²= 5²16+9 = 25
25 = 25.
Hence rope has formed a right-angled triangle because the length of its sides follows Pythagorean Theorem.

Converse of the Pythagorean Theorem – Page No. 386

Question 19.
Justify Reasoning Yoshi has two identical triangular boards as shown. Can he use these two boards to form a rectangle? Explain.
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 2: Converse of the Pythagorean Theorem img 12$

Answer: Since it was proved that both can form a right-angled triangle, we can form a rectangle by joining them.

Explanation: Given both triangles are identical, if both are right-angled triangles then we can surely join to form a rectangle.
Let’s consider a = 0.75, b= 1 and c=1.25.
By using converse Pythagorean Theorem a²+ b²= c²0.75²+ 1²= 1.25²0.5625 + 1 = 1.5625
1.5625 = 1.5625.
Since it was proved that both can form a right-angled triangles, we can form a rectangle by joining them.

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 386 Q20$

FOCUS ON HIGHER ORDER THINKING

Question 21.
Make a Conjecture Diondre says that he can take any right triangle and make a new right triangle just by doubling the side lengths. Is Diondre’s conjecture true? Test his conjecture using three different right triangles.
_______

Answer: Yes, Diondre’s conjecture is true. By doubling the sides of a right triangle would create a new right triangle.

Explanation: Given a right triangle, the Pythagorean Theorem holds. Therefore, a²+ b²= c²If we double the side lengths of that triangle, we get:
(2a)²+ (2b)²= (2c)²
4a²+ 4b²= 4c²
4(a²+ b²) = 4c²
a²+ b²= c² As we can see doubling the sides of a right triangle would create a new right triangle.We can test that by using three different right triangles.

The triangle with sides a = 6, b = 8 and c = 10 is a right triangle. We double its sides and check if the new triangle is a right triangle. After doubling value of a = 12, b = 16 and c = 20.
12² + 16²= 20²
144 + 256 = 400
400 = 400
Hence proved!
Since 12² + 16²= 20², the new triangle is a right triangle by the converse of the Pythagorean Theorem.

The triangle with sides a = 3, b = 4 and c = 5 is a right triangle. We double its sides and check if the new triangle is a right triangle. After doubling value of a = 6, b = 8 and c = 10.
6² + 8²= 10²
36 + 64 = 100
100 = 100
Hence proved!
Since 6² + 8²= 10², the new triangle is a right triangle by the converse of the Pythagorean Theorem.

The triangle with sides a = 12, b = 16 and c = 20 is a right triangle. We double its sides and check if the new triangle is a right triangle. After doubling value of a = 24, b = 32 and c = 40.
24² + 32²= 40²
576 + 1024 = 1600
1600 = 1600
Hence proved!
Since 24² + 32²= 40², the new triangle is a right triangle by the converse of the Pythagorean Theorem.

Question 22.
Draw Conclusions A diagonal of a parallelogram measures 37 inches. The sides measure 35 inches and 1 foot. Is the parallelogram a rectangle? Explain your reasoning.
_______

Answer: Since 12²+ 35²= 37², the triangle is right triangle. Therefore, the given parallelogram is a rectangle.

Explanation: A rectangle is a parallelogram where the interior angles are right angles. To prove if the given parallelogram is a rectangle, we need to prove that the triangle formed by the diagonal of the parallelogram and two sides of it, is a right triangle. Converting all the values into inches, we have a = 12, b = 35 and c = 37. Using the converse of the Pythagorean Theorem, we have:
a²+ b²= c²
12²+ 35²= 37²144 + 1225 = 1369
1369 = 1369.
Since 12²+ 35²= 37², the triangle is right triangle. Therefore, the given parallelogram is a rectangle.

Question 23.
Represent Real-World Problems A soccer coach is marking the lines for a soccer field on a large recreation field. The dimensions of the field are to be 90 yards by 48 yards. Describe a procedure she could use to confirm that the sides of the field meet at right angles.

Answer: To confirm that the sides of the field meet at right angles, she could measure the diagonal of the field and use the converse of the Pythagorean Theorem. If a²+ b²= c²(where a = 90, b = 48, and c is the length of the diagonal), then the triangle is a right triangle. This method can be used for every corner to decide if they form right angles or not.

Guided Practice – Distance Between Two Points – Page No. 390

Question 1.
Approximate the length of the hypotenuse of the right triangle to the nearest tenth using a calculator.
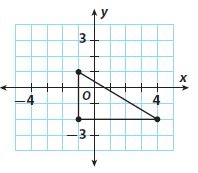
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 3: Distance Between Two Points img 13$
_______ units

Answer: The length of the hypotenuse of the right triangle to the nearest tenth is 5.8 units.

Explanation: From the above figure let’s take
Length of the vertical leg = 3 units
Length of the horizontal leg = 5 units
let length of the hypotenuse = c
By using Pythagorean Theorem a²+ b²= c²c² = 3² + 5²c²= 9 +25
c = √34 => 5.830.
Therefore Length of the hypotenuse of the right triangle to the nearest tenth is 5.8 units.

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 390 Q2$

Question 3.
A plane leaves an airport and flies due north. Two minutes later, a second plane leaves the same airport flying due east. The flight plan shows the coordinates of the two planes 10 minutes later. The distances in the graph are measured in miles. Use the Pythagorean Theorem to find the distance shown between the two planes.
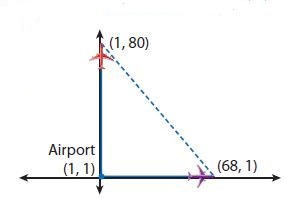
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 3: Distance Between Two Points img 14$
_______ miles

Answer: The distance between the two planes is 103.6 miles.

Explanation:
Length of the vertical d_v= √(80 -1)²+ √(1-1)²
= √79²=> 79.
Length of the horizontal d_{h =}√(68 -1)²+ √(1-1)²
= √67²=> 67.
Distance between the two planes D = √(79² + 67²)
= √(6241+4489) => √10730
= 103.5857 => 103.6 miles.

ESSENTIAL QUESTION CHECK-IN

Question 4.
Describe two ways to find the distance between two points on a coordinate plane.

Answer:

Explanation: We can draw a right triangle whose hypotenuse is the segment connecting the two points and then use the Pythagorean Theorem to find the length of that segment. We can also the Distance formula to find the length of that segment.

For example, plot three points; (1,2), (20,2), and (20,12)

Using the Pythagorean Theorem:

The length of the horizontal leg is the absolute value of the difference between the x-coordinates of points (1,2) and (20,2).
|1 – 20| = 19
The length of the horizontal leg is 19.

The length of the vertical leg is the absolute value of the difference between the y-coordinates of the points (20,2) and (20,12).
|2 – 12| = 10
The length of the vertical leg is 10.

Let a = 19, b = 10 and let c represent the hypotenuse. Find c.
a²+ b²= c²
19²+ 10²= c²
361 + 100 = c²
461 = c²
distance is 21.5 = c

Using the Distance formula:
d= √( x₂– x₁)²+ √( y₂– y₁)²The length of the horizontal leg is between (1,2) and (20,2).
d= √( x₂– x₁)²+ √( y₂– y₁)² = √(20 -1)²+ √(2-2)²
= √(19)²+ √(0)²
= √361 => 19
The length of the vertical leg is between (20,2) and (20,12).
d= √( x₂– x₁)²+ √( y₂– y₁)² = √(20 -20)²+ √(12-2)²
= √(0)²+√(10)²
= √100 => 10
The length of the diagonal leg is between (1,2) and (20,12).
d= √( x₂– x₁)²+ √( y₂– y₁)² = √(20 -1)²+ √(12-2)²
= √(19)²+ √(10)²
= √(361+100) => √461 = 21.5

12.3 Independent Practice – Distance Between Two Points – Page No. 391

Question 5.
A metal worker traced a triangular piece of sheet metal on a coordinate plane, as shown. The units represent inches. What is the length of the longest side of the metal triangle? Approximate the length to the nearest tenth of an inch using a calculator. Check that your answer is reasonable.
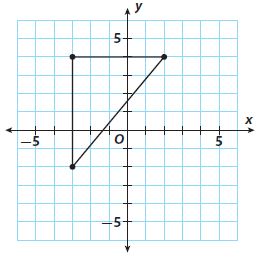
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 3: Distance Between Two Points img 15$
_______ in.

Answer: The length of the longest side of the metal triangle to the nearest tenth is 7.8 units.

Explanation: From the above figure let’s take
Length of the vertical leg = 6 units
Length of the horizontal leg = 5 units
let length of the hypotenuse = c
By using Pythagorean Theorem a²+ b²= c²c² = 6² + 5²c²= 36 +25
c = √61 => 7.8
Therefore Length of the longest side of the metal triangle to the nearest tenth is 7.8 units.

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 391 Q6$

Question 7.
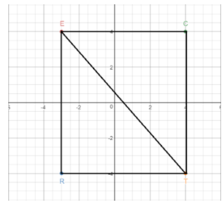
The coordinates of the vertices of a rectangle are given by R(- 3, – 4), E(- 3, 4), C (4, 4), and T (4, – 4). Plot these points on the coordinate plane at the right and connect them to draw the rectangle. Then connect points E and T to form diagonal $\overline { ET } $.
a. Use the Pythagorean Theorem to find the exact length of $\overline { ET } $.
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 3: Distance Between Two Points img 16$

Answer: The diagonal ET is about 10.63 units long.

Explanation:
Taking into consideration the triangle TRE, the length of the vertical leg (ER) is 8 units. The length of the horizontal leg (RT) is 7 units. Let a = 8 and b =7. Let c represent the length of the hypotenuse, the diagonal ET. We use the Pythagorean Theorem to find c.
a²+ b²= c²c² = 8² + 7²c²= 64 +49
c = √113 => 10,63.
The diagonal ET is about 10.63 units long.

Question 7.
b. How can you use the Distance Formula to find the length of $\overline { ET } $ ? Show that the Distance Formula gives the same answer.

Answer: The diagonal ET is about 10.63 units long. As we can see the answer is the same as the one we found using the Pythagorean Theorem.

Explanation: Using the distance formula, in a coordinate plane, the distance d between the points E(-3,4) and T(4, -4) is:
d= √( x₂– x₁)²+ √( y₂– y₁)² = √(4 – (-3))²+ √(- 4 – 4)²
= √(7)²+ √(-8)²
= √(49+64) => √113 = 10.63.
The diagonal ET is about 10.63 units long. As we can see the answer is the same as the one we found using the Pythagorean Theorem.

Question 8.
Multistep The locations of three ships are represented on a coordinate grid by the following points: P(- 2, 5), Q(- 7, – 5), and R(2, – 3). Which ships are farthest apart?

Answer: Ships P and Q are farthest apart

Explanation: Distance Formula: In a coordinate plane, the distance d between two points (x₁,y₁) and (x₂,y₂) is:

d= √( x₂– x₁)²+ √( y₂– y₁)²
The distance d₁between the two points P(-2,5) and Q(-7,-5) is:
d_{1 =} √( x_Q– x_P)²+ √( y_Q– y_P)²
= √(-7 – (-2))²+ √(- 5 – 5)²
= √(-5)²+ √(-10)²
= √(25+100) => √125 = 11.18

The distance d₂between the two points Q(-7,-5) and R(2,-3) is:
d_{3 =} √( x_R– x_Q)²+ √( y_R– y_Q)² = √(2 – (-7))²+ √(- 3 – 5)²
= √(9)²+ √(2)²
= √(81+4) => √85 = 9.22

The distance d₃between the two points P(-2,5) and R(2,-3) is:
d_{3 =} √( x_R– x_P)²+ √( y_R– y_P)²
= √(2 – (-2))²+ √(- 3 – 5)²
= √(4)²+ √(-8)²
= √(16+64) => √80 = 8.94.
As we can see, the greatest distance is d₁11.8, which means that ships P and Q are farthest apart.

Distance Between Two Points – Page No. 392

Question 9.
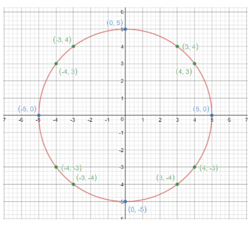
Make a Conjecture Find as many points as you can that are 5 units from the origin. Make a conjecture about the shape formed if all the points 5 units from the origin were connected.

Answer: (0,5), (3,4), (4,3),(5,0),(4,-3),(3,-4),(0,-5),(-3,-4),(-4,-3),(-5,0),(-4,3),(-3,4).

Explanation: Some of the points that are 5 units away from the origin are: (0,5), (3,4), (4,3),(5,0),(4,-3),(3,-4),(0,-5),(-3,-4),(-4,-3),(-5,0),(-4,3),(-3,4) etc, If all the points 5 units away from the origin are connected, a circle would be formed.

Question 10.
Justify Reasoning The graph shows the location of a motion detector that has a maximum range of 34 feet. A peacock at point P displays its tail feathers. Will the motion detector sense this motion? Explain.
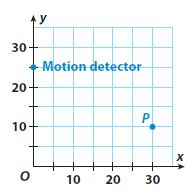
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 3: Distance Between Two Points img 17$

Answer: Considering each unit represents 1 foot, the motion detector, and peacock are 33.5 feet apart. Since the motion detector has a maximum range of 34 feet, it means that it will sense the motion of the peacock’s feathers.

Explanation: The coordinates of the motion detector are said to be (0,25), whereas the coordinates of the peacock are (30,10). In a coordinate plane, the distance d between the points (0,25) and (30,10) is:
d₌ √( x₂– x₁)²+ √( y₂– y₁)²
= √(30 – 0)²+ √(10 – 25)²
= √(30)²+ √(-15)²
= √(900+225) => √1125.
Rounding answer to the nearest tenth:
d = 33.5 feet.
Considering each unit represents 1 foot, the motion detector and peacock are 33.5 feet apart. Since the motion detector has a maximum range of 34 feet, it means that it will sense the motion of the peacock’s feathers.

FOCUS ON HIGHER ORDER THINKING

Question 11.
Persevere in Problem Solving One leg of an isosceles right triangle has endpoints (1, 1) and (6, 1). The other leg passes through the point (6, 2). Draw the triangle on the coordinate plane. Then show how you can use the Distance Formula to find the length of the hypotenuse. Round your answer to the nearest tenth.
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 3: Distance Between Two Points img 18$

Answer: 7.1 units.

Explanation:

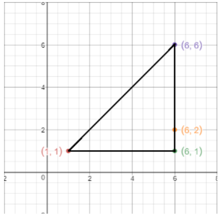
One leg of an isosceles right triangle has endpoints (1,1) and (6,1), which means that the leg is 5 units long. Since the triangle is isosceles, the other leg should be 5 units long too, therefore the endpoints of the second leg that passes through the point (6,2) are (6,1) and (6,6).
In the coordinate plane, the length of the hypotenuse is the distance d between points (1,1) and (6,6).
d₌ √( x₂– x₁)²+ √( y₂– y₁)²
= √(6 – 1)²+ √(6 – 1)²
= √(5)²+ √(5)²
= √(25+25) => √50.
Rounding answer to nearest tenth:
d = 7.1.
The hypotenuse is around 7.1 units long.

Question 12.
Represent Real-World Problems The figure shows a representation of a football field. The units represent yards. A sports analyst marks the locations of the football from where it was thrown (point A) and where it was caught (point B). Explain how you can use the Pythagorean Theorem to find the distance the ball was thrown. Then find the distance.
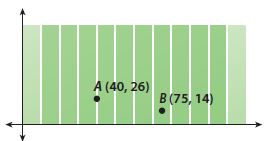
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Lesson 3: Distance Between Two Points img 19$
_______ yards

Answer: The distance between point A and B is 37 yards

Explanation:

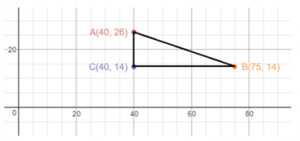
To find the distance between points A and B, we draw segment AB and label its length d. Then we draw the vertical segment AC and Horizontal segment CB. We label the lengths of these segments a and b. triangle ACB is a right triangle with hypotenuse AB.
Since AC is a vertical segment, its length, a, is the difference between its y-coordinates. Therefore, a = 26 – 14 = 12 units.
Since CB is a horizontal segment, its length b is the difference between its x-coordinates. Therefore, b = 75 – 40 = 35units.
We use the Pythagorean Theorem to find d, the length of segment AB.
d²= a²+ b²d²= 12²+ 35²
d² = 144 + 1225
d²= 1369 => d = √1369 => 37
The distance between points A and B is 37 yards

Ready to Go On? – Model Quiz – Page No. 393

12.1 The Pythagorean Theorem

Find the length of the missing side.

Question 1.
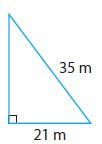
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Model Quiz img 20$
________ meters

Answer: Length of the missing side is 28m

Explanation: Lets consider value of a = 21 and c = 35.
Using Pythagorean Theorem a²+ b²= c²
21²+ b²= 35² 441 + b² = 1225
b²= 784 => b = √784 = 28.
Therefore length of missing side is 28m.

Question 2.
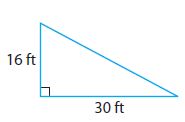
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Model Quiz img 21$
________ ft

Answer: Length of missing side is 34ft

Explanation: Let’s consider value of a = 16 and b = 30.
Using Pythagorean Theorem a²+ b²= c²16²+ 30²= c² 256 + 900 = c²
c²= 1156 => c = √1156 = 34.
Therefore length of missing side is 34ft.

12.2 Converse of the Pythagorean Theorem

Tell whether each triangle with the given side lengths is a right triangle.

Question 3.
11, 60, 61
____________

Answer: Since 11²+ 60²= 61², by the converse of the Pythagorean Theorem, we say that the given sides are in the shape of right-angled triangle.

Explanation: Let a = 11, b = 60 and c= 61
Using the converse of the Pythagorean Theorem a²+ b²= c²11²+ 60²= 61²
121 + 3600 = 3721
3721 = 3721
Since 11²+ 60²= 61², by the converse of the Pythagorean Theorem, we say that the given sides are in the shape of right-angled triangle.

Question 4.
9, 37, 40
____________

Answer: Since 9²+ 37²≠ 40², by the converse of the Pythagorean Theorem, we say that the given sides are not in the shape of a right-angled triangle.

Explanation: Let a = 9, b = 37 and c= 40
Using the converse of the Pythagorean Theorem a²+ b²= c²9²+ 37²= 40²81 + 1369 = 1600
1450 ≠ 3721.
Since 9²+ 37²≠ 40², by the converse of the Pythagorean Theorem, we say that the given sides are not in the shape of a right-angled triangle.

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 393 Q5$

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 393 Q6$

Question 7.
Keelie has a triangular-shaped card. The lengths of its sides are 4.5 cm, 6 cm, and 7.5 cm. Is the card a right triangle?
____________

Answer: Since 4.5²+ 6²= 7.5², by the converse of the Pythagorean Theorem, we say that the given sides are in the shape of a right-angled triangle.

Explanation: Let a = 4.5, b = 6 and c= 7.5
Using the converse of the Pythagorean Theorem a²+ b²= c²4.5²+ 6²= 7.5²20.25 + 36 = 56.25
56.25= 56.25
Since 4.5²+ 6²= 7.5², by the converse of the Pythagorean Theorem, we say that the given sides are in the shape of a right-angled triangle.

12.3 Distance Between Two Points

Find the distance between the given points. Round to the nearest tenth.
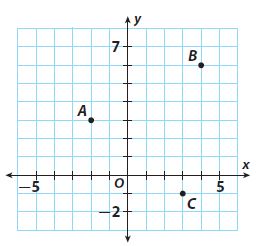
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Model Quiz img 22$

Question 8.
A and B
________ units

Answer: The distance between A and B is 6.7 units

Explanation: A= (-2,3) and B= (4,6)

Distance between A and B is d₌ √( x₂– x₁)²+ √( y₂– y₁)²
= √(4 – (-2)²+ √(6 – 3)²
= √(6)²+ √(3)²
= √(36+9) => √45 = 6.7 units

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 393 Q9$

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 393 Q10$

ESSENTIAL QUESTION

Question 11.
How can you use the Pythagorean Theorem to solve real-world problems?
Answer:
We can use the Pythagorean Theorem to find the length of a side of a right triangle when we know the lengths of the other two sides. This application is usually used in architecture or other physical construction projects. For example, it can be used to find the length of a ladder, if we know the height of the wall and the distance on the ground from the wall of the ladder.

Selected Response – Mixed Review – Page No. 394

Question 1.
What is the missing length of the side?
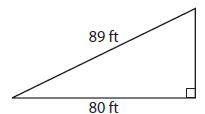
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Mixed Review img 23$
A. 9 ft
B. 30 ft
C. 39 ft
D. 120 ft

Answer: C

$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 394 Q1$

Question 2.
Which relation does not represent a function?
Options:
A. (0, 8), (3, 8), (1, 6)
B. (4, 2), (6, 1), (8, 9)
C. (1, 20), (2, 23), (9, 26)
D. (0, 3), (2, 3), (2, 0)

Answer: D

Explanation: The value of X is the same for 2 points and 2 values of Y [(2, 3), (2, 0)]. The value of X is repeated for a function to exist, no two points can have the same X coordinates.

Question 3.
Two sides of a right triangle have lengths of 72 cm and 97 cm. The third side is not the hypotenuse. How long is the third side?
Options:
A. 25 cm
B. 45 cm
C. 65 cm
D. 121 cm

Answer: C

Explanation:
Given a= 72 cm
b= ?
c= 97 cm
As a²+b²=c²72²+b²= 97²5,184+b²= 9,409
b²= 9,409-5,184
b= √4,225
b= 65 cm.

Question 4.
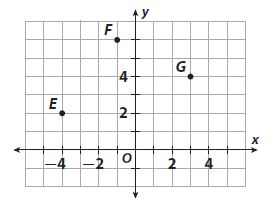
To the nearest tenth, what is the distance between point F and point G?
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Mixed Review img 24$
Options:
A. 4.5 units
B. 5.0 units
C. 7.3 units
D. 20 units

Answer: A.

Explanation:
Given F= (-1,6) =(x1,y1).
G= (3,4) = (x2,y2).
The difference between F&G points is
d= √(x2-x1)² + (y2-y1)²
= √(3 – (-1))² + (4 – 6)² = √(4)² + (-2)²
= √16+4
= √20
= 4.471
= 4.5 units.

Question 5.
A flagpole is 53 feet tall. A rope is tied to the top of the flagpole and secured to the ground 28 feet from the base of the flagpole. What is the length of the rope?
Options:
A. 25 feet
B. 45 feet
C. 53 feet
D. 60 feet

Answer: D

Explanation:

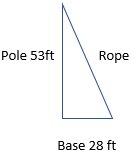
By Pythagorean theorem
a²+b²=c²53²+28²= C²2,809+784= C²
C²= 9,409-5,184
C²= 3,593
C= √3,593
C= 59.94 feet
=60 feet.

Question 6.
Which set of lengths is not the side lengths of a right triangle?
Options:
A. 36, 77, 85
B. 20, 99, 101
C. 27, 120, 123
D. 24, 33, 42

Answer: D.

Explanation:
Check if side lengths in option A form a right triangle.
Let a= 36, b= 77, c= 85
By Pythagorean theorem
a²+b²=c²36²+77²= 85²
1,296+ 5,929= 7,225
7,225= 7,225
As 36²+77²= 85² the triangle is a right triangle.

Check if side lengths in option B form a right triangle.
Let a= 20, b= 99, c= 101
By Pythagorean theorem
a²+b²=c²20²+99²= 101²
400+ 9,801= 10,201
10,201= 10,201
As 20²+99²= 101² the triangle is a right triangle.

Check if side lengths in option B form a right triangle.
Let a= 27, b= 120, c= 123
By Pythagorean theorem
a²+b²=c²27²+120²= 123²
729+ 14,400= 15,129
15,129= 15,129
As 27²+120²= 123²the triangle is a right triangle.

Check if side lengths in option B form a right triangle.
Let a= 27, b= 120, c= 123
By Pythagorean theorem
a²+b²=c²24²+33²= 42²
576+ 1,089= 1,764.
1,665= 1,764
As 24²+33²is not equal to 42²the triangle is a right triangle.

Question 7.
A triangle has one right angle. What could the measures of the other two angles be?
Options:
A. 25° and 65°
B. 30° and 15°
C 55° and 125°
D 90° and 100°

Answer:
A. 25° and 65°

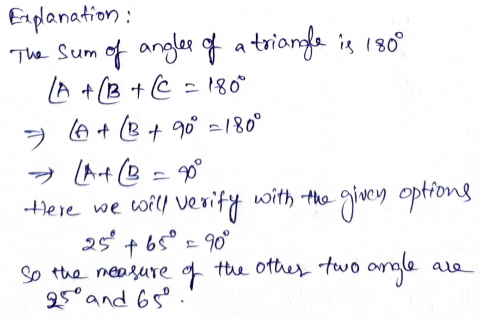
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Page 394 Q7$

Mini-Task

Question 8.
A fallen tree is shown on the coordinate grid below. Each unit represents 1 meter.
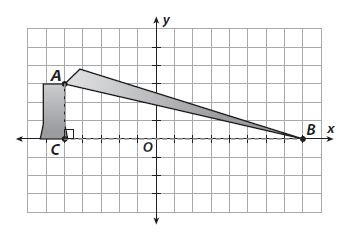
$Go Math Grade 8 Answer Key Chapter 12 The Pythagorean Theorem Mixed Review img 25$
a. What is the distance from A to B?
_______ meters

Answer: 13.34 m.

Explanation:
A= (-5,3)
B= (8,0)
Distance between A & B is
D= √{8-(-5)² + (0-3)² = √(13)² + (-3)²
= √169+9
= √178
= 13.34 m.

Question 8.
b. What was the height of the tree before it fell?
_______ meters

Answer: 16.3 m.

Explanation:
Length of the broken part= 13.3 m
Length of vertical part= 3 m
Total Length = 13.3 m + 3 m
= 16.3 m.

Final Words

In addition to the exercise problems, we have provided the solutions for the review questions. So all the students are requested to test their knowledge and solve the problems provided at the end of this chapter. Refer to HMH Go Math Grade 8 Answer Key and try to score the highest marks in the exams. Hope you liked the explanations provided in this chapter. Stay tuned to get the solutions according to the list of the chapters of all the grades.

Refer:

CANFINHOME Pivot Calculator

Eureka Math Grade 7 Module 2 Lesson 4 Answer Key

December 7, 2023December 6, 2023 by Prasanna

$Eureka Math Grade 7 Module 2 Lesson 4 Answer Key$

Engage NY Eureka Math 7th Grade Module 2 Lesson 4 Answer Key

Eureka Math Grade 7 Module 2 Lesson 4 Example Answer Key

Example 1:
Rule for Adding Integers with Same Signs
a. Represent the sum of 3+5 using arrows on the number line.
$Engage NY Math 7th Grade Module 2 Lesson 4 Example Answer Key 1$
Answer:
$Engage NY Math 7th Grade Module 2 Lesson 4 Example Answer Key 2$
3 + 5 = 8

i. How long is the arrow that represents 3?
Answer:
3 units

b. What direction does it point?
Answer:
Right/up

iii. How long is the arrow that represents 5?
Answer:
5 units

iv. What direction does it point?
Answer:
Right/up

v. What is the sum?
Answer:
8

vi. If you were to represent the sum using an arrow, how long would the arrow be, and what direction would it point?
Answer:
The arrow would be 8 units long and point to the right (or up on a vertical number line).

vii. What is the relationship between the arrow representing the number on the number line and the absolute value of the number?
Answer:
The length of an arrow representing a number is equal to the absolute value of the number.

vii. Do you think that adding two positive numbers will always give you a greater positive number? Why?
Answer:
Yes, because the absolute values are positive, so the sum will be a greater positive. On a number line, adding them would move you farther away from 0 (to the right or above) on a number line.

From part (a), use the same questions to elicit feedback.
→ In the Integer Game, I would combine -3 and -5 to give me -8.

b. Represent the sum of -3 + (-5) using arrows that represent -3 and -5 on the number line.
$Engage NY Math 7th Grade Module 2 Lesson 4 Example Answer Key 5$
Answer:
$Engage NY Math 7th Grade Module 2 Lesson 4 Example Answer Key 6$
-3 + (-5) = -8

i. How long is the arrow that represents -3?
Answer:
3 units

ii. What direction does it point?
Answer:
Left/down

iii. How long is the arrow that represents -5?
Answer:
5 units

iv. What direction does it point?
Answer:
Left/down

iv. What is the sum?
Answer:
-8

vi. If you were to represent the sum using an arrow, how long would the arrow be, and what direction would it point?
Answer:
The arrow would be 8 units long and point to the left (or down on a vertical number line).

vii. Do you think that adding two negative numbers will always give you a smaller negative number? Why?
Answer:
Yes, because the absolute values of negative numbers are positive, so the sum will be a greater positive. However, the opposite of a greater positive is a smaller negative. On a number line, adding two negative numbers would move you farther away from 0 (to the left or below) on a number line.

c. What do both examples have in common?
Answer:
The length of the arrow representing the sum of two numbers with the same sign is the same as the sum of the absolute values of both numbers.

The teacher writes the rule for adding integers with the same sign.

RULE: Add rational numbers with the same sign by adding the absolute values and using the common sign.

Example 2.
Rule for Adding Opposite Signs
a. Represent 5 + (-3) using arrows on the number line.
$Engage NY Math 7th Grade Module 2 Lesson 4 Example Answer Key 9.1$
Answer:
5 + (-3) = 2
$Engage NY Math 7th Grade Module 2 Lesson 4 Example Answer Key 10$

i. How long is the arrow that represents 5?
Answer:
5 units

ii. What direction does it point?
Answer:
Right/up

iii. How long is the arrow that represents -3?
Answer:
3 units

iv. What direction does it point?
Answer:
Left/down

v. Which arrow is longer?
Answer:
The arrow that is five units long, or the first arrow.

vi. What is the sum? If you were to represent the sum using an arrow, how long would the arrow be, and what direction would it point?
Answer:
5 + (-3) = 2
The arrow would be 2 units long and point right/up.

b. Represent the 4 + (-7) using arrows on the number line.
$Engage NY Math 7th Grade Module 2 Lesson 4 Example Answer Key 10.2$
Answer:
4 + (-7) = -3
$Engage NY Math 7th Grade Module 2 Lesson 4 Example Answer Key 11$

i. In the two examples above, what is the relationship between the length of the arrow representing the sum and the lengths of the arrows representing the two addends?
Answer:
The length of the arrow representing the sum is equal to the difference of the absolute values of the lengths of both arrows representing the two addends.

ii. What is the relationship between the direction of the arrow representing the sum and the direction of the arrows representing the two addends?
Answer:
The direction of the arrow representing the sum has the same direction as the arrow of the addend with the greater absolute value.

iii. Write a rule that will give the length and direction of the arrow representing the sum of two values that have opposite signs.
Answer:
The length of the arrow of the sum is the difference of the absolute values of the two addends. The direction of the arrow of the sum is the same as the direction of the longer arrow.

The teacher writes the rule for adding integers with opposite signs.

RULE: Add rational numbers with opposite signs by subtracting the absolute values and using the sign of the integer with the greater absolute value

Example 3.
Applying Integer Addition Rules to Rational Numbers
Find the sum of 6 + (-2$\frac{1}{4}$). The addition of rational numbers follows the same rules of addition for integers.
a. Find the absolute values of the numbers.
Answer:
|6| = 6
|-2$\frac{1}{4}$| = 2 $\frac{1}{4}$

b. Subtract the absolute values.
6 – 2$\frac{1}{4}$ = 6 – $\frac{9}{4}$ = $\frac{24}{4}$ – $\frac{9}{4}$ = $\frac{15}{4}$ = 3$\frac{3}{4}$
Answer:
$Engage NY Math 7th Grade Module 2 Lesson 4 Example Answer Key 25$

c. The answer will take the sign of the number that has the greater absolute value.
Answer:
Since 6 has the greater absolute value (arrow length), my answer will be positive 3 $\frac{3}{4}$ .

Eureka Math Grade 7 Module 2 Lesson 3 Exercise Answer Key

$Eureka Math Grade 7 Module 2 Lesson 3 Exercise Answer Key$

Exercise 2.
a. Decide whether the sum will be positive or negative without actually calculating the sum.
i. -4 + (-2) ___
Answer:
Negative

ii. 5 + 9 ___
Answer:
Positive

iii. -6 + (-3) ____
Answer:
Negative

iv. -1 + (-11) ___
Answer:
Negative

v. 3 + 5 + 7 ___
Answer:
Positive

vi. -20 + (-15) __
Answer:
Negative

b. Find the sum.

i. 15 + 7
Answer:
22

ii. -4 + (-16)
Answer:
-20

iii. -18 + (-64)
Answer:
-82

iv. -205 + (-123)
Answer:
-328

Exercise 3.
Circle the integer with the greater absolute value. Decide whether the sum will be positive or negative without actually calculating the sum.

i. -1 + 2
Answer:
$Eureka Math Grade 7 Module 2 Lesson 4 Exercise Answer Key 25.1$

ii. 5 + (-9)
Answer:
$Eureka Math Grade 7 Module 2 Lesson 4 Exercise Answer Key 26$

iii. -6 + 3
Answer:
$Eureka Math Grade 7 Module 2 Lesson 4 Exercise Answer Key 27$

iv. -11 + 1
Answer:
$Eureka Math Grade 7 Module 2 Lesson 4 Exercise Answer Key 28$

b. Find the sum.

i. -10 + 7
Answer:
-3

ii. 8 + (-16)
Answer:
-8

iii. -12 + (65)
Answer:
53

iv. 105 + (-126)
Answer:
-21

Exercise 4.
Solve the following problems. Show your work.
a. Find the sum of $Eureka Math Grade 7 Module 2 Lesson 4 Exercise Answer Key 60$
Answer:
|-18| = 18
|7| = 7
18 – 7 = 11
-11

b. If the temperature outside was 73 degrees at 5:00 p.m., but it fell 19 degrees by 10:00 p.m., what is the temperature at 10:00 p.m.? Write an equation and solve.
Answer:
$Eureka Math Grade 7 Module 2 Lesson 4 Exercise Answer Key 65$

c. Write an addition sentence, and find the sum using the diagram below.
$Eureka Math Grade 7 Module 2 Lesson 4 Exercise Answer Key 65.1$
Answer:
$Eureka Math Grade 7 Module 2 Lesson 4 Exercise Answer Key 66$

Eureka Math Grade 7 Module 2 Lesson 3 Exit Ticket Answer Key

Question 1.
Write an addition problem that has a sum of -4 $\frac{4}{5}$ and
a. The two addends have the same sign.
Answer:
Answers will vary. -1 $\frac{4}{5}$ + (-3) = -4 $\frac{4}{5}$ .

b. The two addends have different signs.
Answer:
Answers will vary. 1.8 + (-6.6) = -4.8.

Question 2.
In the Integer Game, what card would you need to draw to get a score of 0 if you have a -16, -35, and 18 in your hand?
Answer:
-16 + (-35) + 18 = -33, so I would need to draw a 33 because 33 is the additive inverse of -33.
-33 + 33 = 0.

Eureka Math Grade 7 Module 2 Lesson 3 Problem Set Answer Key

$Eureka Math Grade 7 Module 2 Lesson 3 Problem Set Answer Key$

Question 1.
Find the sum. Show your work to justify your answer.
a. 4 + 17
Answer:
4 + 17 = 21

b. -6 + (-12)
Answer:
-6 + (-12) = -18

c. 2.2 + (-3.7)
Answer:
2.2 + (-3.7) = -1.5

d. -3 + (-5) + 8
Answer:
-3 + (-5) + 8 = -8 + 8 = 0

e. $\frac{1}{3}$ +(-2 $\frac{1}{4}$)
Answer:
$\frac{1}{3}$ +(-2 $\frac{1}{4}$) = $\frac{1}{3}$ + (-$\frac{9}{4}$ ) = $\frac{4}{12}$ + (-$\frac{27}{12}$ )= – $\frac{23}{12}$ = -1$\frac{11}{12}$

Question 2.
Which of these story problems describes the sum 19+(-12)? Check all that apply. Show your work to justify your answer.
___ Jared’s dad paid him $19 for raking the leaves from the yard on Wednesday. Jared spent $12 at the movie theater on Friday. How much money does Jared have left?
Answer:
X

___ Jared owed his brother $19 for raking the leaves while Jared was sick. Jared’s dad gave him $12 for doing his chores for the week. How much money does Jared have now?

___ Jared’s grandmother gave him $19 for his birthday. He bought $8 worth of candy and spent another $4 on a new comic book. How much money does Jared have left over?
Answer:
X

Question 3.
Use the diagram below to complete each part.
$Eureka Math Grade 7 Module 2 Lesson 4 Problem Set Answer Key 70$
Answer:
$Eureka Math Grade 7 Module 2 Lesson 4 Problem Set Answer Key 70.1$
a. Label each arrow with the number the arrow represents.

b. How long is each arrow? What direction does each arrow point?
$Eureka Math Grade 7 Module 2 Lesson 4 Problem Set Answer Key 72$
Answer:
$Eureka Math Grade 7 Module 2 Lesson 4 Problem Set Answer Key 73$

c. Write an equation that represents the sum of the numbers. Find the sum.
Answer:
5 + (-3) + (-7) = -5

Question 4.
Jennifer and Katie were playing the Integer Game in class. Their hands are represented below.
$Eureka Math Grade 7 Module 2 Lesson 4 Problem Set Answer Key 74$
a. What is the value of each of their hands? Show your work to support your answer.
Answer:
Jennifer’s hand has a value of -3 because 5 + (-8) = -3. Katie’s hand has a value of -2 because
-9 + 7 = -2.

b. If Jennifer drew two more cards, is it possible for the value of her hand not to change? Explain why or why not.
Answer:
It is possible for her hand not to change. Jennifer could get any two cards that are the exact opposites such as (-2) and 2. Numbers that are exact opposites are called additive inverses, and they sum to 0. Adding the number 0 to anything will not change the value.

c. If Katie wanted to win the game by getting a score of 0, what card would she need? Explain.
Answer:
Katie would need to draw a 2 because the additive inverse of -2 is 2. -2 + 2 = 0.

d. If Jennifer drew -1 and -2, what would be her new score? Show your work to support your answer.
Answer:
Jennifer’s new score would be -6 because -3 + (-1) + (-2) = -6.