Similar triangles are triangles that have the same shape, but their sizes may vary. Two triangles are said to be similar if they follow the conditions of similar triangles theorems. Check the different criteria of similarity between triangles along with proof. Also, get the solved example questions.
Criteria of Similarity between Triangles
Similar triangles are the triangles that look similar to each other but their sizes may vary. Two objects are called similar if they have the same shape irrespective of their size. To prove that the two triangles are similar, we need to follow some conditions. Those conditions are the different criteria for the similarity between triangles. The criterion of similarity statement with proof is mentioned here:
1. SSS Criterion of Similarity:
According to SSS (Side-Side-Side) Similarity criterion, if the corresponding sides of the ratio of two triangles are equal, then two triangles are similar to each other.

In the above image, if \(\frac { AB }{ ZX } \) = \(\frac { BC }{ XY } \) = \(\frac { AC }{ ZY } \)
According to SSS similarity criteria, △ABC ~ △XYZ.
Also, Get
2. SAS (Side-Angle-Side) Criterion of Similarity:
SAS Similarity theorem states that, if any two sides of one triangle are in exact proportion to the two sides of the other triangle and the angle formed the two sides of the triangles are equal, then the triangles must be similar. This condition is applied only, when you know the measure of two sides and include the angle of both triangles.
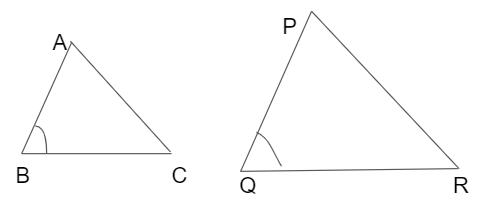
In the above image, if it is \(\frac { AB }{ PQ } \) = \(\frac { BC }{ QR } \) and ∠CBA = ∠RQP, then △ABC ~ △PQR as per SAS criterion of similarity.
3. AA (or AAA) or Angle-Angle Criterion of Similarity:
As per the Angle-Angle Similarity criterion, any two angles in the first triangle are equal to the corresponding angles of the second triangle, then those two triangles are similar triangles. This rule is applied when only we know the measure of the angles.
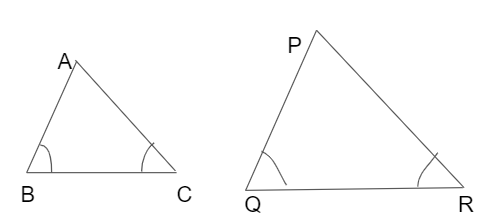
In the image, If ∠B = ∠Q and ∠C = ∠R, then △ABC ~ △PQR according to the AA Similarity criterion.
Problems on Triangle Similarity Theorems
Problem 1:
A person is 120 in tall. He is standing 360 in away from the lamp post. His shadow from the light is 40 in long. Here lamp post is AB. How high is the lamp post?
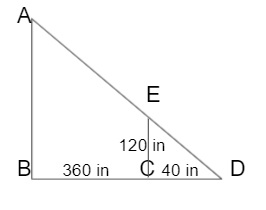
Solution:
Taking △ABD and △ECD, we can see that
∠B = ∠C = 90° and ∠D = ∠D (common angle)
By AA criterion of similarity, △ABD ~ △ECD
Therefore, \(\frac { AB }{ EC } \) = \(\frac { BD }{ CD } \) = \(\frac { AD }{ ED } \)
\(\frac { AB }{ 120 } \) = \(\frac { 360+40 }{ 40 } \)
AB = 1200
So, the height of the lamp is 1200 in.
Problem 2:
If ∆XYZ is similar to ∆PQR and XM, PN are corresponding medians of the triangles respectively, show that \(\frac { XY }{ PQ } \) = \(\frac { XM }{ PN } \).
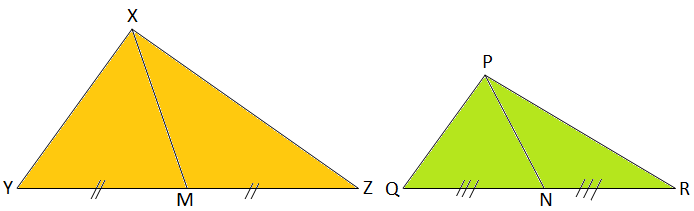
Solution:
In ∆XYM and ∆PQN,
∠Y = ∠Q
\(\frac { XY }{ PQ } \) = \(\frac { YM }{ QN } \) (∆XYZ ∼ ∆PQR and YM = ½YZ, QN = ½QR)
So, ∆XYM ∼ ∆PQN
Therefore, \(\frac { XY }{ PQ } \) = \(\frac { XM }{ PN } \)
Hence proved.
Problem 3:
Prove that ∆ABC ∼ ∆XYZ

Solution:
Given that,
AB = 5 in, BC = 2 in, AC = 7 in
XY = 6 in, XZ = 15 in, ZY = 21 in
\(\frac { AB }{ XZ } \) = \(\frac { 5 }{ 15 } \) = \(\frac { 1 }{ 3 } \)
\(\frac { BC }{ XY } \) = \(\frac { 2 }{ 6 } \) = \(\frac { 1 }{ 3 } \)
\(\frac { AC }{ ZY } \) = \(\frac { 7 }{ 21 } \) = \(\frac { 1 }{ 3 } \)
So, \(\frac { AB }{ XZ } \) = \(\frac { BC }{ XY } \) = \(\frac { AC }{ ZY } \)
Therefore, using SSS similarity criteria ∆ABC ∼ ∆XYZ.
FAQ’s on Criteria For Similarity Of Triangles
1. What are different similarity criteria?
The various similarity criterion of triangles of SSS similarity theorem, SAS similarity theorem and AA similarity theorem.
2. What are similar triangles?
Two triangles are similar when they have the same ratio of corresponding sides and equal pair of corresponding angles.
3. How to find the missing side of similar triangles?
The missing side of a similar triangle can be found by comparing the ratio of the corresponding sides of the triangles. We compare the ratios to get the length of the unknown side of the triangle.