Engage NY Eureka Math 4th Grade Module 3 Lesson 3 Answer Key
Eureka Math Grade 4 Module 3 Lesson 3 Sprint Answer Key
Squares and Unknown Factors

Answer:
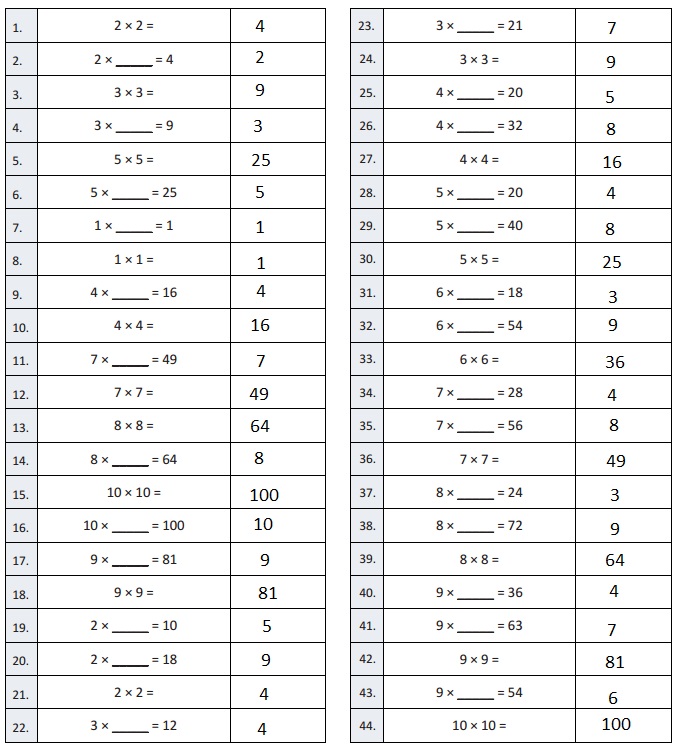
Question 1.
2 × 2 =
Answer:
2 X 2 = 4,
Explanation:
Given 2 X 2 = the squares of 2 is 4 and
2 X 2 = 4.
Question 2.
2 × _____ = 4
Answer:
2 X 2 = 4,
Explanation:
Given 2 × _____ = 4, the unknown factor is
4 ÷ 2 = 2, So 2 X 2 = 4.
Question 3.
3 × 3 =
Answer:
3 X 3 = 9,
Explanation:
Given 3 X 3 = the squares of 3 is 9 and
3 X 3 = 9.
Question 4.
3 × _____ = 9
Answer:
3 X 3 = 9,
Explanation:
Given 3 × _____ = 9, the unknown factor is
9 ÷ 3 = 2, So 3 X 3 = 9.
Question 5.
5 × 5 =
Answer:
5 X 5 = 25,
Explanation:
Given 5 X 5 = the squares of 5 is 25 and
5 X 5 = 25.
Question 6.
5 × _____ = 25
Answer:
5 X 5 = 25,
Explanation:
Given 5 × _____ = 25, the unknown factor is
25 ÷ 5 = 5, So 5 X 5 = 25.
Question 7.
1 × _____ = 1
Answer:
1 x 1 = 1,
Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.
Question 8.
1 × 1 =
Answer:
1 X 1 = 1,
Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.
Question 9.
4 × _____ = 16
Answer:
4 X 4 = 16,
Explanation:
Given 4 × _____ = 16, the unknown factor is
16 ÷ 4 = 1, So 4 X 4 = 16.
Question 10.
4 × 4 =
Answer:
4 X 4 = 16,
Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.
Question 11.
7 × _____ = 49
Answer:
7 X 7 = 49,
Explanation:
Given 7 × _____ = 49, the unknown factor is
49 ÷ 7 = 7, So 7 X 7 = 49.
Question 12.
7 × 7 =
Answer:
7 X 7 = 49,
Explanation:
Given 7 X 7 = the squares of 7 is 49 and
7 X 7 = 49.
Question 13.
8 × 8 =
Answer:
8 X 8 = 64,
Explanation:
Given 8 X 8 = the squares of 8 is 64 and
8 X 8 = 64.
Question 14.
8 × _____ = 64
Answer:
8 X 8 = 64,
Explanation:
Given 8 × _____ = 64, the unknown factor is
64 ÷ 8 = 8, So 8 X 8 = 64.
Question 15.
10 × 10 =
Answer:
10 X 10 = 100,
Explanation:
Given 10 X 10 = the squares of 10 is 100 and
10 X 10 = 100.
Question 16.
10 × _____ = 100
Answer:
10 X 10 = 100,
Explanation:
Given 10 × _____ = 100, the unknown factor is
100 ÷ 10 = 10, So 10 X 10 = 100.
Question 17.
9 × _____ = 81
Answer:
9 X 9 = 81,
Explanation:
Given 9 × _____ = 81, the unknown factor is
81 ÷ 9 = 9, So 9 X 9 = 81.
Question 18.
9 × 9 =
Answer:
9 x 9 = 81,
Explanation:
Given 9 X 9 = the squares of 9 is 81 and
9 X 9 = 81.
Question 19.
2 × _____ = 10
Answer:
2 X 5 = 10,
Explanation:
Given 2 × _____ = 10, the unknown factor is
10 ÷ 2 = 5, So 2 X 5 = 10.
Question 20.
2 × _____ = 18
Answer:
2 X 9 = 18,
Explanation:
Given 2 × _____ = 18, the unknown factor is
18 ÷ 2 = 9, So 2 X 9 = 18.
Question 21.
2 × 2 =
Answer:
2 x 2 = 4,
Explanation:
Given 2 X 2 = the squares of 2 is 4 and
2 X 2 = 4.
Question 22.
3 × _____ = 12
Answer:
3 X 4 = 12,
Explanation:
Given 3 × _____ = 12, the unknown factor is
12 ÷ 3 = 4, So 3 X 4 = 12.
Question 23.
3 × _____ = 21
Answer:
3 X 7 = 21,
Explanation:
Given 3 × _____ = 21, the unknown factor is
21 ÷ 3 = 7, So 3 X 7 = 21.
Question 24.
3 × 3 =
Answer:
3 X 3 = 9,
Explanation:
Given 3 X 3 = the squares of 3 is 9 and
3 X 3 = 9.
Question 25.
4 × _____ = 20
Answer:
4 X 5 = 20,
Explanation:
Given 4 × _____ = 20, the unknown factor is
20 ÷ 4 = 5, So 4 X 5 = 20.
Question 26.
4 × _____ = 32
Answer:
4 X 8 = 32,
Explanation:
Given 4 × _____ = 32, the unknown factor is
32 ÷ 4 = 8, So 4 X 8 = 32.
Question 27.
4 × 4 =
Answer:
4 X 4 = 16,
Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.
Question 28.
5 × _____ = 20
Answer:
5 X 4 = 20,
Explanation:
Given 5 × _____ = 20, the unknown factor is
20 ÷ 5 = 4, So 5 X 4 = 20.
Question 29.
5 × _____ = 40
Answer:
5 X 8 = 40,
Explanation:
Given 5 × _____ = 40, the unknown factor is
40 ÷ 5 = 8, So 5 X 8 = 40.
Question 30.
5 × 5 =
Answer:
5 X 5 = 25,
Explanation:
Given 5 X 5 = the squares of 5 is 25 and
5 X 5 = 25.
Question 31.
6 × _____ = 18
Answer:
6 X 3 = 18,
Explanation:
Given 6 × _____ = 18, the unknown factor is
18 ÷ 6 = 3, So 6 X 3 = 18.
Question 32.
6 × _____ = 54
Answer:
6 X 9 = 54,
Explanation:
Given 6 × _____ = 18, the unknown factor is
54 ÷ 6 = 9, So 6 X 9 = 54.
Question 33.
6 × 6 =
Answer:
6 X 6 = 36,
Explanation:
Given 6 X 6 = the squares of 6 is 36 and
6 X 6 = 36.
Question 34.
7 × _____ = 28
Answer:
7 X 4 = 28,
Explanation:
Given 7 × _____ = 28, the unknown factor is
28 ÷ 4 = 7, So 7 X 4 = 28.
Question 35.
7 × _____ = 56
Answer:
7 X 8 = 56,
Explanation:
Given 7 × _____ = 56, the unknown factor is
56 ÷ 7 = 8, So 7 X 8 = 56.
Question 36.
7 × 7 =
Answer:
7 X 7 = 49,
Explanation:
Given 7 X 7 = 49 the squares of 7 is 49 and
7 X 7 = 49.
Question 37.
8 × _____ = 24
Answer:
8 X 3 = 24,
Explanation:
Given 8 × _____ = 24, the unknown factor is
24 ÷ 8 = 3, So 8 X 3 = 24.
Question 38.
8 × _____ = 72
Answer:
8 X 9 = 72,
Explanation:
Given 8 × _____ = 72, the unknown factor is
72 ÷ 8 = 9, So 8 X 9 = 72.
Question 39.
8 × 8 =
Answer:
8 X 8 = 64,
Explanation:
Given 8 X 8= 64 the squares of 8 is 64 and
8 X 8 = 64.
Question 40.
9 × _____ = 36
Answer:
9 X 4 = 36,
Explanation:
Given 9 × _____ = 36, the unknown factor is
36 ÷ 9 = 4, So 9 X 4 = 36.
Question 41.
9 × _____ = 63
Answer:
9 X 7 = 63,
Explanation:
Given 9 × _____ = 63, the unknown factor is
63 ÷ 9 = 7, So 9 X 7 = 63.
Question 42.
9 × 9 =
Answer:
9 x 9 = 81,
Explanation:
Given 9 X 9= 81 the squares of 9 is 81 and
9 X 9 = 81.
Question 43.
9 × _____ = 54
Answer:
9 X 6 = 54,
Explanation:
Given 9 × _____ = 54, the unknown factor is
54 ÷ 9 = 6, So 9 X 6 = 54.
Question 44.
10 × 10 =
Answer:
10 X 10 = 100,
Explanation:
Given 10 X 10= 100 the squares of 10 is 100 and
10 X 10 = 100.
Squares and Unknown Factors

Answer:
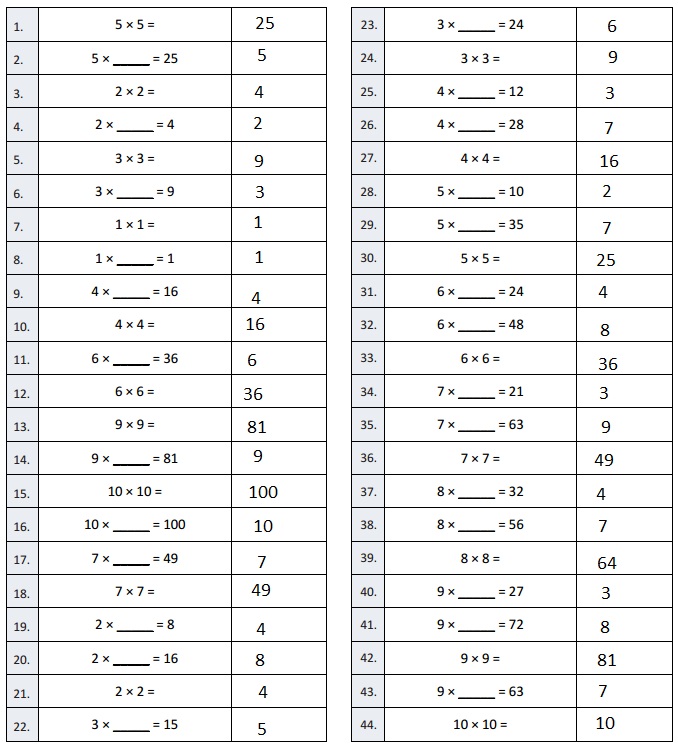
Question 1.
5 × 5 =
Answer:
5 X 5 = 25,
Explanation:
Given 5 X 5= 25 the squares of 5 is 25 and
5 X 5 = 25.
Question 2.
5 × _____ = 25
Answer:
5 X 5 = 25,
Explanation:
Given 5 × _____ = 25, the unknown factor is
25 ÷ 5 = 5, So 5 X 5 = 25.
Question 3.
2 × 2 =
Answer:
2 X 2 = 4,
Explanation:
Given 2 X 2= 4 the squares of 2 is 4 and
2 X 2 = 4.
Question 4.
2 × _____ = 4
Answer:
2 X 2 = 4,
Explanation:
Given 2 × _____ = 4, the unknown factor is
4 ÷ 2 = 2, So 2 X 2 = 4.
Question 5.
3 × 3 =
Answer:
3 X 3 = 9,
Explanation:
Given 3 X 3= 9 the squares of 3 is 9 and
3 X 3 = 9.
Question 6.
3 × _____ = 9
Answer:
3 x 3 = 9,
Explanation:
Given 3 × _____ = 9, the unknown factor is
9 ÷ 3 = 3, So 3 X 3 = 9.
Question 7.
1 × 1 =
Answer:
1 X 1 = 1,
Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.
Question 8.
1 × _____ = 1
Answer:
1 x 1 = 1,
Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.
Question 9.
4 × _____ = 16
Answer:
4 X 4 = 16,
Explanation:
Given 4 × _____ = 16, the unknown factor is
16 ÷ 4 = 1, So 4 X 4 = 16.
Question 10.
4 × 4 =
Answer:
4 X 4 = 16,
Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.
Question 11.
6 × _____ = 36
Answer:
6 X 6 = 36,
Explanation:
Given 6 × _____ = 36, the unknown factor is
36 ÷ 6 = 6, So 6 X 6 = 36.
Question 12.
6 × 6 =
Answer:
6 X 6 = 36,
Explanation:
Given 6 X 6 = the squares of 6 is 36 and
6 X 6 = 36.
Question 13.
9 × 9 =
Answer:
9 x 9 = 81,
Explanation:
Given 9 X 9 = the squares of 9 is 81 and
9 X 9 = 81.
Question 14.
9 × _____ = 81
Answer:
9 X 9 = 81,
Explanation:
Given 9 × _____ = 81, the unknown factor is
81 ÷ 9 = 9, So 9 X 9 = 81.
Question 15.
10 × 10 =
Answer:
10 X 10 = 100,
Explanation:
Given 10 X 10 = the squares of 10 is 100 and
10 X 10 = 100.
Question 16.
10 × _____ = 100
Answer:
10 X 10 = 100,
Explanation:
Given 10 × _____ = 100, the unknown factor is
100 ÷ 10 = 10, So 10 X 10 = 100.
Question 17.
7 × _____ = 49
Answer:
7 X 7 = 49,
Explanation:
Given 7 × _____ = 49, the unknown factor is
49 ÷ 7 = 7, So 7 X 7 = 49.
Question 18.
7 × 7 =
Answer:
7 X 7 = 49,
Explanation:
Given 7 X 7 = the squares of 7 is 49 and
7 X 7 = 49.
Question 19.
2 × _____ = 8
Answer:
2 X 4 = 8,
Explanation:
Given 2 × _____ = 8, the unknown factor is
8 ÷ 2 = 4, So 2 X 4 = 8.
Question 20.
2 × _____ = 16
Answer:
2 X 8 = 16,
Explanation:
Given 2 × _____ = 16, the unknown factor is
16 ÷ 2 = 8, So 2 X 8 = 16.
Question 21.
2 × 2 =
Answer:
2 X 2 = 4,
Explanation:
Given 2 X 2 = the squares of 2 is 4 and
2 X 2 = 4.
Question 22.
3 × _____ = 15
Answer:
3 X 5 = 15,
Explanation:
Given 3 × _____ = 15, the unknown factor is
15 ÷ 3 = 5, So 3 X 5 = 15.
Question 23.
3 × _____ = 24
Answer:
3 X 8 = 24,
Explanation:
Given 3 × _____ = 24, the unknown factor is
24 ÷ 3 = 8, So 3 X 8 = 24.
Question 24.
3 × 3 =
Answer:
3 X 3 = 9,
Explanation:
Given 3 X 3 = the squares of 3 is 9 and
3 X 3 = 9.
Question 25.
4 × _____ = 12
Answer:
Explanation:
Given 4 × _____ = 12, the unknown factor is
12 ÷ 4 = 3, So 4 X 3 = 12.
Question 26.
4 × _____ = 28
Answer:
4 X 7 = 28,
Explanation:
Given 4 × _____ = 28, the unknown factor is
28 ÷ 4 = 7, So 4 X 7 = 28.
Question 27.
4 × 4 =
Answer:
4 X 4 = 16,
Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.
Question 28.
5 × _____ = 10,
Answer:
5 X 2 = 10,
Explanation:
Given 5 × _____ = 10, the unknown factor is
10 ÷ 5 = 2, So 5 X 2 = 10.
Question 29.
5 × _____ = 35,
Answer:
5 X 7 = 35,
Explanation:
Given 5 × _____ = 10, the unknown factor is
35 ÷ 5 = 7, So 5 X 7 = 35.
Question 30.
5 × 5 =
Answer:
5 X 5 = 25,
Explanation:
Given 5 X 5 = the squares of 5 is 25 and
5 X 5 = 25.
Question 31.
6 × _____ = 24
Answer:
6 X 4 = 24,
Explanation:
Given 6 × _____ = 24, the unknown factor is
24 ÷ 6 = 4, So 6 X 4 = 24.
Question 32.
6 × _____ = 48
Answer:
6 X 8 = 48,
Explanation:
Given 6 × _____ = 48, the unknown factor is
48 ÷ 6 = 8, So 6 X 8 = 48.
Question 33.
6 × 6 =
Answer:
6 X 6 = 36,
Explanation:
Given 6 × _____ = 36, the unknown factor is
36 ÷ 6 = 6, So 6 X 6 = 36.
Question 34.
7 × _____ = 21
Answer:
7 X 3 = 21,
Explanation:
Given 7 × _____ = 21, the unknown factor is
21 ÷ 7 = 3, So 7 X 3 = 21.
Question 35.
7 × _____ = 63
Answer:
7 X 9 = 63,
Explanation:
Given 7 × _____ = 63, the unknown factor is
63 ÷ 7 = 9, So 7 X 9 = 63.
Question 36.
7 × 7 =
Answer:
7 X 7 = 49,
Explanation:
Given 7 X 7 = the squares of 7 is 49 and
7 X 7 = 49.
Question 37.
8 × _____ = 32
Answer:
8 X 4 = 32,
Explanation:
Given 8 × _____ = 32, the unknown factor is
32 ÷ 8 = 4, So 8 X 4 = 32.
Question 38.
8 × _____ = 56
Answer:
8 X 7 = 56,
Explanation:
Given 8 × _____ = 56, the unknown factor is
56 ÷ 8 = 7, So 8 X 7 = 56.
Question 39.
8 × 8 =
Answer:
8 X 8 = 64,
Explanation:
Given 8 X 8 = the squares of 8 is 64 and
8 X 8 = 64.
Question 40.
9 × _____ = 27
Answer:
9 X 3 = 27,
Explanation:
Given 9 × _____ = 27, the unknown factor is
27 ÷ 9 = 3, So 9 X 3 = 27.
Question 41.
9 × _____ = 72
Answer:
9 X 8 = 72,
Explanation:
Given 9 × _____ = 72, the unknown factor is
72 ÷ 9 = 8, So 9 X 8 = 72.
Question 42.
9 × 9 =
Answer:
9 X 9 = 81,
Explanation:
Given 9 X 9 = the squares of 8 is 64 and
9 X 9 = 81.
Question 43.
9 × _____ = 63
Answer:
9 X 7 = 63,
Explanation:
Given 9 × _____ = 63, the unknown factor is
63 ÷ 9 = 7, So 9 X 7 = 63.
Question 44.
10 × 10 =
Answer:
10 X 10 = 100,
Explanation:
Given 10 X 10 = the squares of 10 is 100 and
10 X 10 = 100.
Eureka Math Grade 4 Module 3 Lesson 3 Problem Set Answer Key
Solve the following problems. Use pictures, numbers, or words to show your work.
Question 1.
The rectangular projection screen in the school auditorium is 5 times as long and 5 times as wide as the rectangular screen in the library. The screen in the library is 4 feet long with a perimeter of 14 feet. What is the perimeter of the screen in the auditorium?
Answer:
The perimeter of the screen in the auditorium is 70 feet,
Explanation:
Given the rectangular projection screen in the school auditorium is 5 times as long and 5 times as wide as the rectangular screen in the library. The screen in the library is 4 feet long with a perimeter of 14 feet. Let wide of of screen in library be w feet,
so 14 feet = 2 X (4 feet + w feet),
14 feet = 8 feet + 2 X w feet,
2 X w feet = 14 feet – 8 feet = 6 feet,
So wide = 6 feet ÷ 2 = 3 feet,
Now the rectangular projection screen in the school auditorium
is 5 X 4 feet = 20 feet long and wide is 5 X 3 feet = 15 feet wide,
So the perimeter of the screen in the auditorium is
2 X (20 feet + 15 feet) = 2 X 35 feet = 70 feet.
Question 2.
The width of David’s rectangular tent is 5 feet. The length is twice the width. David’s rectangular air mattress measures 3 feet by 6 feet. If David puts the air mattress in the tent, how many square feet of floor space will be available for the rest of his things?
Answer:
32 square feet of floor space will be available for the rest of his things,
Explanation:
Given the width of David’s rectangular tent is 5 feet. The length is twice the width.
David’s rectangular air mattress measures
3 feet by 6 feet. Area of the rectangular tent is
5 feet X ( 2 X 5 feet) = 5 feet X 10 feet = 50 square feet,
now David’s rectangular air mattress area is 3 feet x 6 feet =
18 square feet,
If David puts the air mattress in the tent, number of square feet of floor space will be available for the rest of his things is 50 square feet – 18 square feet = 32 square feet.
Question 3.
Jackson’s rectangular bedroom has an area of 90 square feet. The area of his bedroom is 9 times that of his rectangular closet. If the closet is 2 feet wide, what is its length?
Answer:
The closet length is 5 feet,
Explanation:
Given Jackson’s rectangular bedroom has an area of 90 square feet.
The area of his bedroom is 9 times that of his rectangular closet.
So closet area is 90 X feet X feet ÷ 9 = 10 square feet,
As given closet is 2 feet wide, the length will be
10 feet X feet = 2 feet X length of the closet,
length of the closet = 10 feet x feet ÷ 2 feet = 5 feet.
therefore the length of the closer is 5 feet.
Question 4.
The length of a rectangular deck is 4 times its width. If the deck’s perimeter is 30 feet, what is the deck’s area?
Answer:
The area of the deck is 36 square feet,
Explanation:
Given the length of a rectangular deck is 4 times its width.
If the deck’s perimeter is 30 feet, then
30 feet = 2 X (4 X width + width) ,
30 feet ÷ 2 = 5 X width,
15 feet = 5 width
therefore width = 15 feet ÷ 5 = 3 feet and
length = 4 X 3 feet = 12 feet,
Now the area of the deck is 12 feet X 3 feet = 36 square feet.
Eureka Math Grade 4 Module 3 Lesson 3 Exit Ticket Answer Key
Solve the following problem. Use pictures, numbers, or words to show your work.
A rectangular poster is 3 times as long as it is wide. A rectangular banner is 5 times as long as it is wide. Both the banner and the poster have perimeters of 24 inches. What are the lengths and widths of the poster and the banner?
Answer:
The rectangular poster is 9 inches long and 3 inches wide,
The rectangular banner is 10 inches long and 2 inches wide,
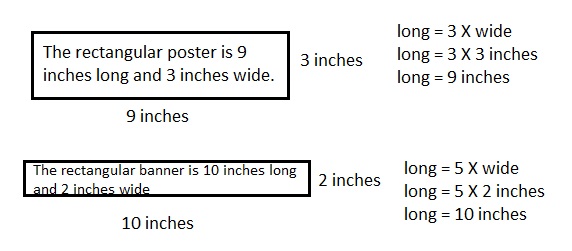
Explanation:
Given a rectangular poster is 3 times as long as it is wide.
A rectangular banner is 5 times as long as it is wide.
Both the banner and the poster have perimeters of 24 inches.
First rectangular poster, So 24 inches = 2 X (3 X wide + wide),
24 inches ÷ 2 = 4 wide,
12 inches = 4 wide
therefore wide = 12 inches ÷ 4 = 3 inches and
long =3 X 3 inches = 9 inches,
Now rectangular banner, 24 inches = 2 X (5 X wide + wide),
24 inches ÷ 2 = 6 wide,
12 inches = 6 wide,
wide = 12 inches ÷ 6 = 2 inches, and long = 5 X 2 inches = 10 inches,
Shown the work above in the picture,
Therefore, The rectangular poster is 9 inches long and 3 inches wide,
The rectangular banner is 10 inches long and 2 inches wide.
Eureka Math Grade 4 Module 3 Lesson 3 Homework Answer Key
Solve the following problems. Use pictures, numbers, or words to show your work.
Question 1.
Katie cut out a rectangular piece of wrapping paper that was 2 times as long and 3 times as wide as the box that she was wrapping. The box was 5 inches long and 4 inches wide. What is the perimeter of the wrapping paper that Katie cut?
Answer:
The perimeter of the wrapping paper that Katie cut is 44 inches,

Explanation:
Given Katie cut out a rectangular piece of wrapping paper that was
2 times as long and 3 times as wide as the box that she
as wrapping. The box was 5 inches long and 4 inches wide.
So the wrapping paper length is 2 X 5 inches = 10 inches and
width is 3 X 4 inches = 12 inches, Now the perimeter of the
wrapping paper that Katie cut is 2 X (10 inches + 12 inches) =
2 X 22 inches = 44 inches. Shown the work above in the picture,
therefore, the perimeter of the wrapping paper that Katie cut is 44 inches.
Question 2.
Alexis has a rectangular piece of red paper that is 4 centimeters wide. Its length is twice its width. She glues a rectangular piece of blue paper on top of the red piece measuring 3 centimeters by 7 centimeters. How many square centimeters of red paper will be visible on top?
Answer:
11 square centimeters of red paper will be visible on top,
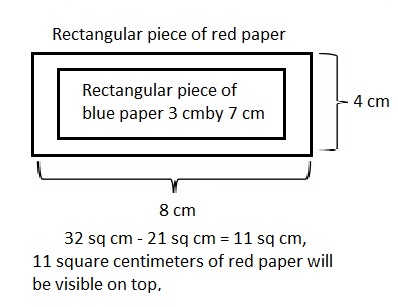
Explanation:
Given Alexis has a rectangular piece of red paper that is
4 centimeters wide. Its length is twice its width.
She glues a rectangular piece of blue paper on top
of the red piece measuring 3 centimeters by 7 centimeters.
Area of rectangular piece of red paper = 4 cm X ( 2 X 4 cm) =
4 cm X 8 cm = 32 square cm, Now area of rectangular piece
of blue paper on top of the red piece is 3 cm X 7 cm = 21 square cm,
So number of square centimeters of red paper will be visible on top
is 32 sq cm – 21 sq cm = 11 sq cm. Shown the work above in the picture,
Therefore, 11 square centimeters of red paper will be visible on top.
Question 3.
Brinn’s rectangular kitchen has an area of 81 square feet. The kitchen is 9 times as many square feet as Brinn’s pantry. If the rectangular pantry is 3 feet wide, what is the length of the pantry?
Answer:
The length of the pantry is 3 feet,
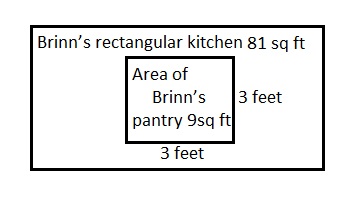
Explanation:
Given Brinn’s rectangular kitchen has an area of 81 square feet.
The kitchen is 9 times as many square feet as Brinn’s pantry.
So area of Brinn’s pantry is 81 sq feet ÷ 9 = 9 sq feet,
Given the rectangular pantry is 3 feet wide so
length of the pantry is 9 sq feet ÷ 3 feet = 3 feet,
Shown the work above in the picture, therefore
the length of the pantry is 3 feet.
Question 4.
The length of Marshall’s rectangular poster is 2 times its width. If the perimeter is 24 inches, what is the area of the poster?
Answer:
The area of the Marshall’s poster is 32 square inches,

Explanation:
Given the length Marshall’s rectangular poster is 2 times its width
and the perimeter is 24 inches, so 24 inches = 2 X (2 X width + width),
24 inches ÷ 2 = 3 X width,
12 inches = 3 X width
So width = 12 inches ÷ 3 = 4 inches, length = 2 X 4 inches = 8 inches,
now area of the poster is 8 inches X 4 inches = 32 square inches,
Shown the work above in the picture, therefore
The area of the poster is 32 square inches.