Engage NY Eureka Math Precalculus Module 1 Lesson 14 Answer Key
Eureka Math Precalculus Module 1 Lesson 14 Exercise Answer Key
Exercises
The vertices A(0, 0), B(1, 0), C(1, 1), and D(0, 1) of a unit square can be represented by the complex numbers A = 0, B = 1, C = 1 + i, and D = i.
Exercise 1.
Let L1(z) = – z.
a. Calculate A’ = L1(A), B’ = L1(B), C’ = L1(C), and D’ = L1(D). Plot these four points on the axes.
b. Describe the geometric effect of the linear transformation L1(z) = – z on the square ABCD.
Answer:
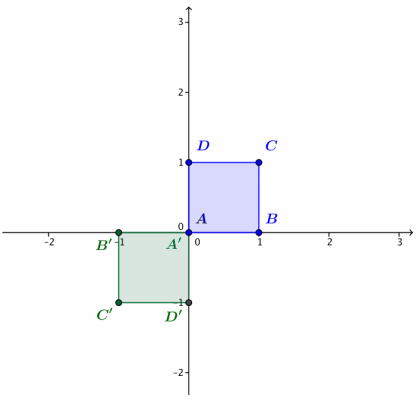
Transformation L1rotates the square ABCD by 180° about the origin.
Exercise 2.
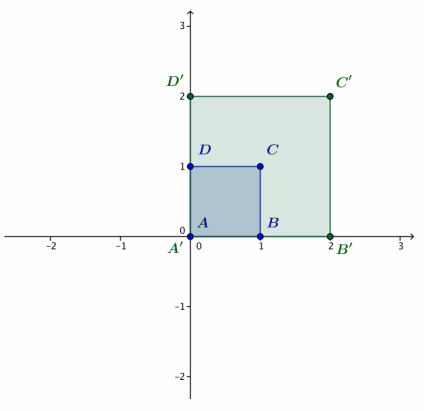
Let L2(z) = 2z.
a. Calculate A’ = L2(A), B’ = L2(B), C’ = L2(C), and D = L2(D). Plot these four points on the axes.
b. Describe the geometric effect of the linear transformation L2(z) = 2z on the square ABCD.
Answer:
Transformation L2dilates the square ABCD by a factor of 2.
Exercise 3.
Let L3(z) = iz.
a. Calculate A’ = L3(A), B’ = L3(B), C’ = L3(C), and D’ = L3(D). Plot these four points on the axes.
b. Describe the geometric effect of the linear transformation L3(z) = iz on the square ABCD.
Answer:
Transformation L3rotates the square ABCD by 90° counterclockwise about the origin.
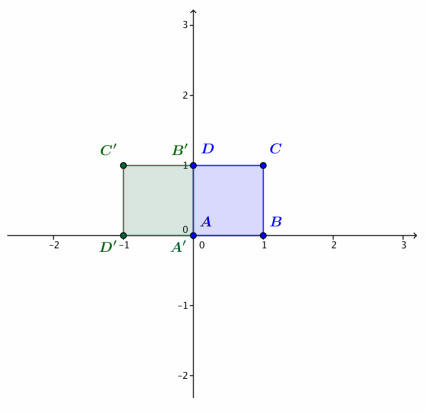
Exercise 4.
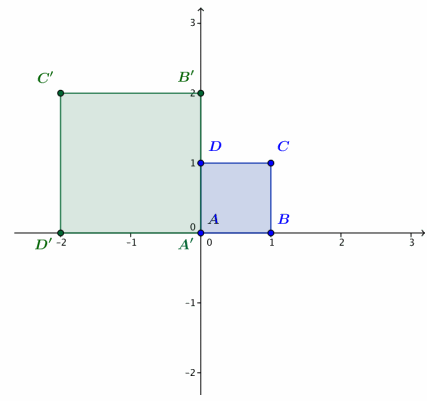
Let L4(z) = (2i)z.
a. Calculate A’ = L4(A), B’ = L4(B), C’ = L4(C), and D’ = L4(D). Plot these four points on the axes.
b. Describe the geometric effect of the linear transformation L4(z) = (2i)z on the square ABCD.
Answer:
Transformation L4rotates the square ABCD by 90° counterclockwise about the origin and dilates by a factor of 2.
Exercise 5.
Explain how transformations L2, L3, and L4are related.
Answer:
Transformation L4is the result of doing transformations L2and L3(in either order).
Discussion
→ What is the geometric effect of the transformation L(z) = az for a real number a>0?
→ The effect of L is dilation by the factor a.
→ What happens to a unit square in this case?
→ The orientation of the square does not change; it is not reflected or rotated, but the sides of the square are dilated by a.
→ What is the effect on the square if a>1?
→ The sides of the square will get larger.
→ What is the effect on the square if 0<a<1?
→ The sides of the square will get smaller.
→ What is the geometric effect of the transformation L(z) = az if a = 0?
→ If a = 0, then L(z) = 0 for every complex number z. This transformation essentially shrinks the square down to the point at the origin.
→ What is the geometric effect of the transformation L(z) = az for a real number a<0?
→ If a<0, then L(z) = az = – |a|z , so L is a dilation by |a| and a rotation by 180°. This transformation will dilate the original unit square and then rotate it about point A into the third quadrant.
→ What is the geometric effect of the transformation L(z) = (bi)z for a real number b>0?
→ The transformation L dilates by b and rotates by 90° counterclockwise.
→ What is the effect on the unit square if b>1?
→ The sides of the square will get larger.
→ What is the effect on the unit square if 0<b<1?
→ The sides of the square will get smaller.
→ What is the effect on the unit square if b<0?
→ If b<0, then L(z) = (bi)z = i(bz), so L is a dilation by |b| and a rotation by 180°, followed by a rotation by 90°. This transformation will rotate and dilate the original unit square and then rotate it about point A to the fourth quadrant.
Exercise 6.
We will continue to use the unit square ABCD with A = 0, B = 1, C = 1 + i, D = i for this exercise.
a. What is the geometric effect of the transformation L(z) = 5z on the unit square?
Answer:
By our work in the first five exercises and the previous discussion, we know that this transformation dilates the unit square by a factor of 5.
b. What is the geometric effect of the transformation L(z) = (5i)z on the unit square?
Answer:
By our work in the first five exercises, this transformation will dilate the unit square by a factor of 5 and rotate it 90° counterclockwise about the origin.
c. What is the geometric effect of the transformation L(z) = (5i2)z on the unit square?
Answer:
Since i2 = – 1, this transformation is L(z) = – 5z, which will dilate the unit square by 5 and rotate it 180° about the origin.
d. What is the geometric effect of the transformation L(z) = (5i3)z on the unit square?
Answer:
Since i3 = – i, this transformation is L(z) = ( – 5i)z, which will dilate the unit square by a factor of 5 and rotate it 270° counterclockwise about the origin.
e. What is the geometric effect of the transformation L(z) = (5i4)z on the unit square?
Answer:
Since i4 = (i2)2 = ( – 1)2 = 1, this transformation is L(z) = 5z, which is the same transformation as in part (a). Thus, this transformation dilates the unit square by a factor of 5.
f. What is the geometric effect of the transformation L(z) = (5i5)z on the unit square?
Answer:
Since i5 = i4 ∙ i = i, this is the same transformation as in part (b). This transformation will dilate the unit square by a factor of 5 and rotate it 90° counterclockwise about the origin.
g. What is the geometric effect of the transformation L(z) = (5in)z on the unit square, for some integer
n≥0?
Answer:
If n is a multiple of 4, then L(z) = (5in)z = 5z will dilate the unit square by a factor of 5.
If n is one more than a multiple of 4, then L(z) = (5in)z = (5i)z will dilate the unit square by a factor of 5 and rotate it 90° counterclockwise about the origin.
If n is two more than a multiple of 4, then L(z) = (5in)z = – 5z will dilate the unit square by 5 and rotate it 180° about the origin.
If n is three more than a multiple of 4, then L(z) = (5in)z = ( – 5i)z will dilate the unit square by a factor of 5 and rotate it 270° counterclockwise about the origin.
Eureka Math Precalculus Module 1 Lesson 14 Exploratory Challenge Answer Key
Exploratory Challenge
Your group has been assigned either to the 1 – team, 2 – team, 3 – team, or 4 – team. Each team will answer the questions below for the transformation that corresponds to their team number:
L1(z) = (3 + 4i)z
L2(z) = ( – 3 + 4i)z
L3(z) = ( – 3 – 4i)z
L4(z) = (3 – 4i)z.
The unit square ABCD with A = 0, B = 1, C = 1 + i, D = i is shown below. Apply your transformation to the vertices of the square ABCD, and plot the transformed points A’, B’, C’, and D’ on the same coordinate axes.
The solution shown below is for transformation L1. The transformed square for L2, L3, and L4will be rotated 90°, 180°, and 270° counterclockwise about the origin from the one shown, respectively.
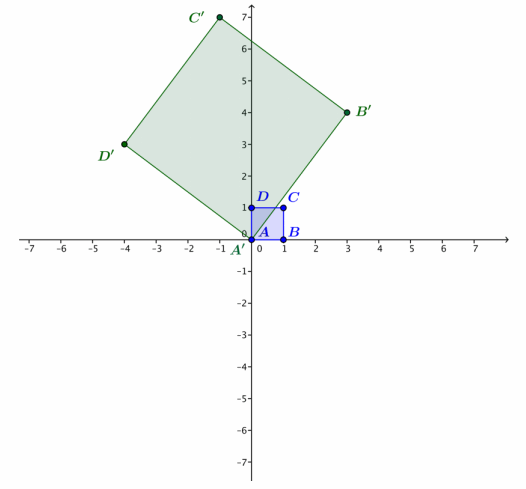
For the 1 – team:
a. Why is B’ = 3 + 4i?
Answer:
Because B = 1, we have B’ = L1(B) = (3 + 4i)(1) = 3 + 4i.
b. What is the argument of 3 + 4i?
Answer:
The argument of 3 + 4i is the amount of counterclockwise rotation between the positive x – axis and the ray connecting the origin and the point (3, 4).
c. What is the modulus of 3 + 4i?
Answer:
The modulus of 3 + 4i is |3 + 4i| = \(\sqrt{3^{2} + 4^{2}}\) = \(\sqrt{25}\) = 5.
For the 2 – team:
a. Why is B’ = – 3 + 4i?
Answer:
Because B = 1, we have B’ = L2(B) = ( – 3 + 4i)(1) = – 3 + 4i.
b. What is the argument of – 3 + 4i?
Answer:
The argument of – 3 + 4i is the amount of counterclockwise rotation between the positive x – axis and the ray connecting the origin and the point ( – 3, 4).
c. What is the modulus of – 3 + 4i?
Answer:
The modulus of – 3 + 4i is | – 3 + 4i| = √(( – 3)2 + 42) = \(\sqrt{2}\)5 = 5.
For the 3 – team:
a. Why is B’ = – 3 – 4i?
Answer:
Because B = 1, we have B’ = L3(B) = ( – 3 – 4i)(1) = – 3 – 4i.
b. What is the argument of – 3 – 4i?
Answer:
The argument of – 3 – 4i is the amount of counterclockwise rotation between the positive x – axis and the ray connecting the origin and the point ( – 3, – 4).
c. What is the modulus of – 3 – 4i?
Answer:
The modulus of – 3 – 4i is | – 3 – 4i| = \(\sqrt{( – 3)^{2} + ( – 4)^{2}}\) = \(\sqrt{25}\) = 5.
For the 4 – team:
a. Why is B’ = 3 – 4i?
Answer:
Because B = 1, we have B’ = L4(B) = (3 – 4i)(1) = 3 – 4i.
b. What is the argument of 3 – 4i?
Answer:
The argument of 3 – 4i is the amount of counterclockwise rotation between the positive x – axis and the ray connecting the origin and the point (3, – 4).
c. What is the modulus of 3 – 4i?
Answer:
The modulus of 3 – 4i is |3 – 4i| = \(\sqrt{3^{2} + ( – 4)^{2}}\) = \(\sqrt{25}\) = 5.
All groups should also answer the following:
a. Describe the amount the square has been rotated counterclockwise.
Answer:
The square has been rotated the amount of counterclockwise rotation between the positive x – axis and ray \(\overrightarrow{A B^{\prime}}\).
b. What is the dilation factor of the square? Explain how you know.
Answer:
First, we need to calculate the length of one side of the square. The length AB’ is given by
AB’ = \(\sqrt{(4 – 0)^{2} + (3 – 0)^{2} = 5}\). Then, the dilation factor of the square is 5 because the final square has sides that are five times longer than the sides of the original square.
c. What is the geometric effect of your transformation L1, L2, L3, or L4on the unit square ABCD?
Answer:
(Answered for transformation L1.) The transformation rotates the square counterclockwise by the argument of (3 + 4i) and dilates it by a factor of the modulus of 3 + 4i.
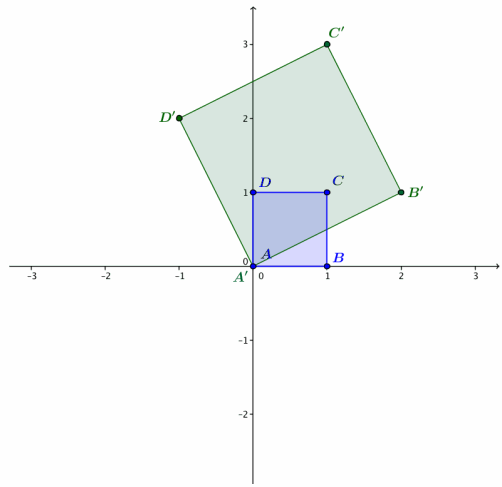
d. Make a conjecture: What do you expect to be the geometric effect of the transformation L(z) = (2 + i)z on the unit square ABCD?
Answer:
This transformation should rotate the square counterclockwise by the argument of 2 + i and dilate it by a factor of |2 + i| = \(\sqrt{2^{2} + 1^{2}}\) = \(\sqrt{5}\).
e. Test your conjecture with the unit square on the axes below.
Answer:
Eureka Math Precalculus Module 1 Lesson 14 Exit Ticket Answer Key
Question 1.
Identify the linear transformation L that takes square ABCD to square A’B’C’D’ as shown in the figure on the right.
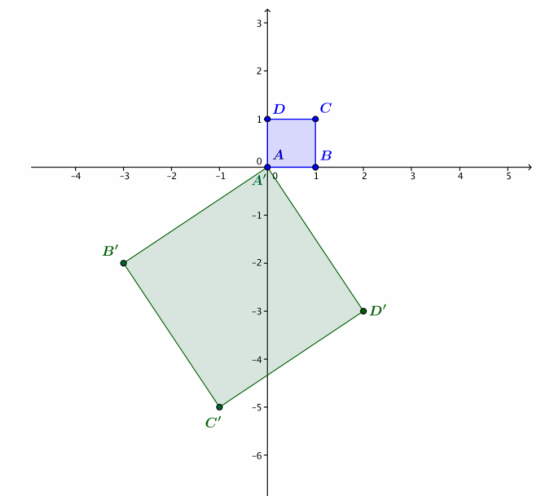
Answer:
The transformation L takes the point B = 1 to the point B’ = – 3 – 2i, so this transformation is given by L(z) = ( – 3 – 2i)z.
Question 2.
Describe the geometric effect of the transformation L(z) = (1 – 3i)z on the unit square ABCD, where A = 0, B = 1, C = 1 + i, and D = i. Sketch the unit square transformed by L on the axes on the right.
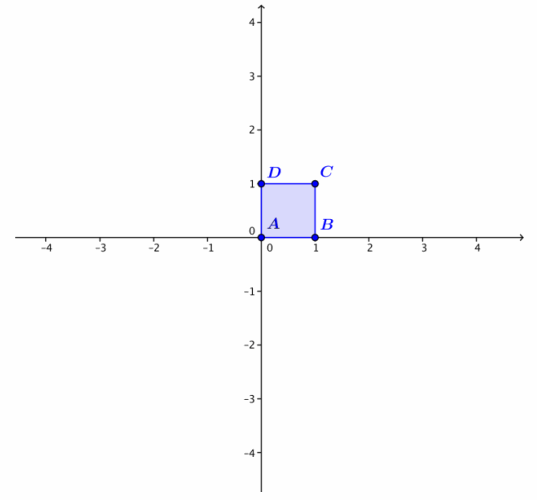
Answer:
This transformation dilates by |1 – 3i| = \(\sqrt{1^{2} + 3^{2}}\) = \(\sqrt{10}\) and rotates counterclockwise by arg(1 – 3i).
Eureka Math Precalculus Module 1 Lesson 14 Problem Set Answer Key
Question 3.
Find the modulus and argument for each of the following complex numbers.
a. z1 = \(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\)i
Answer:
\(\left|\frac{\sqrt{3}}{2} + \frac{1}{2} i\right|\) = 1, z1 is in Quadrant I; thus, arg(z1) = arctan(\(\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}\)) = 30° = \(\frac{\pi}{6}\) rad.
b. z2 = 2 + 2\(\sqrt{3}\)i
Answer:
|2 + 2\(\sqrt{3}\)i| = 4, z2 is in Quadrant I; thus, arg(z2) = arctan((2\(\sqrt{3}\))/( 2 )) = 60° = \(\frac{π}{3}\)rad.
c. z3 = – 3 + 5i
Answer:
|3 + 5i| = \(\sqrt{34}\), z3is in Quadrant II; thus, arg(z) = π – arctan(\(\frac{5}{3}\))≈π – 1.030≈2.112 rad.
d. z4 = – 2 – 2i
Answer:
| – 2 – 2i| = 2\(\sqrt{2}\), z4is in Quadrant III; thus, arg(z4) = π + arctan(\(\frac{2}{2}\)) = π + \(\frac{π}{4}\) = \(\frac{5π}{4}\) rad.
e. z5 = 4 – 4i
Answer:
|4 + 4i| = 4\(\sqrt{2}\), z5 is in Quadrant IV; thus, arg(z5 ) = 2π – arctan(\(\frac{4}{4}\)) = 2π – ( \(\frac{π}{4}\)) = ( 7\(\frac{π}{4}\)) rad.
f. z6 = 3 – 6i
Answer:
|3 – 6i| = 3\(\sqrt{5}\), z6 is in Quadrant IV; thus, arg(z6 ) = 2π – arctan(\(\frac{6}{3}\)) = 2π – 1.107 = 5.176 rad.
Question 4.
For parts (a)–(c), determine the geometric effect of the specified transformation.
a. L(z) = – 3z
Answer:
The transformation L dilates by 3 and rotates by 180° about the origin.
b. L(z) = – 100z
Answer:
The transformation L dilates by 100 and rotates by 180° about the origin.
c. L(z) = – \(\frac{1}{3}\)z
Answer:
The transformation L dilates by \(\frac{1}{3}\)and rotates by 180° about the origin.
d. Describe the geometric effect of the transformation L(z) = az for any negative real number a.
Answer:
The transformation L dilates by |a| and rotates by 180° about the origin.
Question 5.
For parts (a)–(c), determine the geometric effect of the specified transformation.
a. L(z) = ( – 3i)z
Answer:
The transformation L dilates by 3 and rotates counterclockwise by 270° about the origin.
b. L(z) = ( – 100i)z
Answer:
The transformation L dilates by 100 and rotates by 270° about the origin.
c. L(z) = ( – \(\frac{1}{3}\)i)z
Answer:
The transformation L dilates by \(\frac{1}{3}\)and rotates counterclockwise by 270° about the origin.
d. Describe the geometric effect of the transformation L(z) = (bi)z for any negative real number b.
Answer:
The transformation L dilates by |b| and rotates by 270° counterclockwise about the origin.
Question 6.
Suppose that we have two linear transformations, L1(z) = 3z and L2(z) = (5i)z.
a. What is the geometric effect of first performing transformation L1and then performing transformation L2?
Answer:
The transformation L1dilates by 3, dilates by 5, and rotates by 90° counterclockwise about the origin.
b. What is the geometric effect of first performing transformation L2and then performing transformation L1?
Answer:
The transformation L1dilates by 5, rotates by 90° counterclockwise about the origin, and then dilates by 3.
c. Are your answers to parts (a) and (b) the same or different? Explain how you know.
Answer:
The answers are the same.
L2(L1(z)) = (5i) L1(z) = (5i)(3z) = (15i)z For example, let z = 2 – 3i.
L1 = 3(2 – 3i) = 6 – 9i
L2 = (5i)(2 – 3i) = 15 + 10i
L2(L1) = (5i)(6 – 9i) = 45 + 30i
L1(L2) = 3(15 + 10i) = 45 + 30i
L1(L2(z)) = 3L2(z) = 3((5i)z) = (15i)z
Question 7.
Suppose that we have two linear transformations, L1(z) = (4 + 3i)z and L2(z) = – z. What is the geometric effect of first performing transformation L1and then performing transformation L2?
Answer:
We have |4 + 3i| = 5, and the argument of 4 + 3i is arctan(\(\frac{3}{4}\))≈0.644 radians, which is about 36.87°. Therefore, the transformation L1 followed by L2dilates with scale factor 5, rotates by approximately 36.87° counter clockwise, and then rotates by 180°.
Question 8.
Suppose that we have two linear transformations, L1(z) = (3 – 4i)z and L2(z) = – z. What is the geometric effect of first performing transformation L1and then performing transformation L2?
Answer:
We see that |3 – 4i| = 5, and the argument of 3 – 4i is arctan(\(\frac{4}{3}\))≈2π – 5.356 radians, which is about 306.87°. Therefore, the transformation L1followed by L2dilates with scale factor 5, rotates by approximately 306.87° counter clockwise, and then rotates by 180°.
Question 9.
Explain the geometric effect of the linear transformation L(z) = (a – bi)z, where a and b are positive real numbers.
Answer:
Note that the complex number a – bi is represented by a point in the fourth quadrant. The transformation L dilates with scale factor |a – bi| and rotates counterclockwise by 2π – arctan(\(\frac{b}{a}\)).
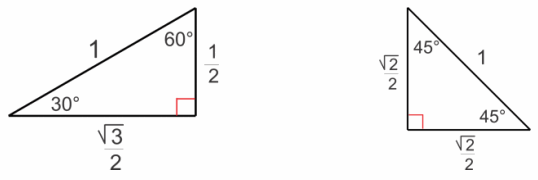
Question 10.
In Geometry, we learned the special angles of a right triangle whose hypotenuse is 1 unit. The figures are shown above. Describe the geometric effect of the following transformations.
a. L1(z) = (\(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\)i)z
|\(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\)i| = 1″, ” arg(z) = 30° = π/6 rad
The transformation L1 rotates counterclockwise by 30°.
b. L2(z) = (2 + 2\(\sqrt{3}\)i)z
Answer:
|2 + 2\(\sqrt{3}\)i| = 4, arg(z) = 60° = \(\frac{π}{3}\)rad
The transformation L2 dilates with scale factor 4 and rotates counterclockwise by 60°.
c. L3(z) = (\(\frac{\sqrt{2}}{2}\) + \(\frac{\sqrt{2}}{2}\)i)z
|\(\frac{\sqrt{2}}{2}\) + \(\frac{\sqrt{2}}{2}\)i| = 1, arg(z) = 45° = \(\frac{π}{4}\) rad
The transformation L3 dilates by 1 and rotates counterclockwise by 45°.
d. L4(z) = (4 + 4i)z
Answer:
|4 + 4i| = 4\(\sqrt{2}\), arg(z) = 45° = \(\frac{π}{4}\) rad
The transformation L4dilates with scale factor 4\(\sqrt{2}\) and rotates counterclockwise by 45°.
Question 11.
Recall that a function L is a linear transformation if all z and w in the domain of L and all constants a meet the following two conditions:
i. L(z + w) = L(z) + L(w)
ii. L(az) = aL(z)
Show that the following functions meet the definition of a linear transformation.
a. L1(z) = 4z
Answer:
L1(z + w) = 4(z + w) = 4z + 4w = L1(z) + L1(w)
L1(az) = 4(az) = 4az = a(4z) = aL1(z)
b. L2(z) = iz
Answer:
L2(z + w) = i(z + w) = iz + iw = L2(z) + L1(w)
L2(az) = i(az) = iaz = a(iz) = aL2(z)
c. L3(z) = (4 + i)z
Answer:
L3(z + w) = (4 + i)(z + w) = (4 + i)z + (4 + i)w = L3(z) + L3(w)
L3(az) = (4 + i)(az) = (4 + i)az = a((4 + i)z) = aL3(z)
Question 12.
The vertices A(0, 0), B(1, 0), C(1, 1), D(0, 1) of a unit square can be represented by the complex numbers A = 0, B = 1, C = 1 + i, D = i. We learned that multiplication of those complex numbers by i rotates the unit square by 90° counterclockwise. What do you need to multiply by so that the unit square will be rotated by 90° clockwise?
Answer:
We need to multiply by i3 = – i.