Engage NY Eureka Math Precalculus Module 1 Lesson 28 Answer Key
Eureka Math Precalculus Module 1 Lesson 28 Example Answer Key
Example
What transformation reverses a pure dilation from the origin with a scale factor of k?
a. Write the pure dilation matrix, and multiply it by \(\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\).
Answer:
\(\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\left[\begin{array}{ll}
k & 0 \\
0 & k
\end{array}\right]\) = \(\left[\begin{array}{ll}
a k & c k \\
b k & d k
\end{array}\right]\)
b. What values of a,b,c, and d would produce the identity matrix? (Hint: Write and solve a system of equations.)
Answer:
\(\left[\begin{array}{ll}
a k & c k \\
b k & d k
\end{array}\right]\) = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
ak=1,
a= \(\frac{1}{k}\)
ck=0,
c=0,
bk=0,
b=0,
dk=1
d = \(\frac{1}{k}\)
c. Write the matrix, and confirm that it reverses the pure dilation with a scale factor of k.
Answer:
\(\left[\begin{array}{ll}
\frac{1}{k} & 0 \\
0 & \frac{1}{k}
\end{array}\right]\left[\begin{array}{cc}
k & 0 \\
0 & k
\end{array}\right]\) = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Eureka Math Precalculus Module 1 Lesson 28 Exercise Answer Key
Opening Exercise
Perform the operation \(\left[\begin{array}{cc}
3 & -2 \\
1 & 1
\end{array}\right]\) on the unit square.
a. State the vertices of the transformation.
Answer:
(0,0), (3,1), (-2,1), and (1,2)
b. Explain the transformation in words.
Answer:
(0,0) stays at the origin, the vertex (1,0) moves to (3,1), (0,1) moves to (-2,1), and (1,1) moves to (1,2).
c. Find the area of the transformed figure.
Answer:
|(3)(1)-(-2)(1)|=5
The area is 5 units2.
d. If the original square was 2×2 instead of a unit square, how would the transformation change?
Answer:
The coordinates of the vertices of the image would all double. The vertices would be (0,0), (6,2), (-4,2), and (2,4).
e. What is the area of the image? Explain how you know.
Answer:
The area of the image is 20 square units. The area of the original square was 4 square units; multiply that by the determinant, which is 5, and the area of the new figure is 4×5=20 square units.
Exercises
Find the inverse matrix and verify.
Exercise 1.
\(\left[\begin{array}{ll}
1 & 0 \\
1 & 1
\end{array}\right]\)
Answer:
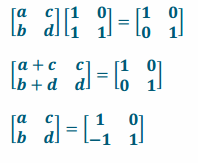
Exercise 2.
\(\left[\begin{array}{ll}
3 & 1 \\
5 & 2
\end{array}\right]\)
Answer:
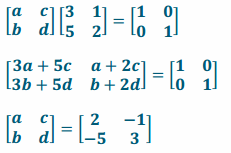
Exercise 3.
\(\left[\begin{array}{cc}
-2 & -5 \\
1 & 2
\end{array}\right]\)
Answer:
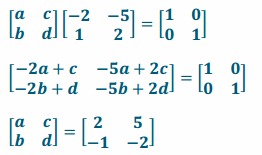
Eureka Math Precalculus Module 1 Lesson 28 Problem Set Answer Key
Question 1.
In this lesson, we learned RθR-θ=\(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\). Chad was saying that he found an easy way to find the inverse matrix, which is Rθ=\(\frac{\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]}{\bar{R}_{\theta}}\). His argument is that if we have 2x=1, then x=\(\frac{1}{2}\).
a. Is Chad correct? Explain your reason.
Answer:
Chad is not correct. Matrices cannot be divided.
b. If Chad is not correct, what is the correct way to find the inverse matrix?
Answer:
To find the inverse of Rθ, calculate the determinant, switch the terms on the forward diagonal and change the signs on the back diagonal, and then divide all terms by the absolute value of the determinant.
Question 2.
Find the inverse matrix and verify it.
a. \(\left[\begin{array}{ll}
3 & 2 \\
7 & 5
\end{array}\right]\)
Answer:
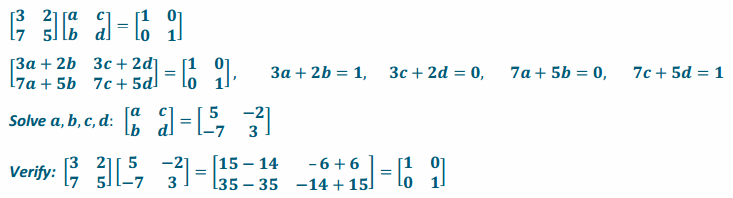
b. \(\left[\begin{array}{cc}
-2 & -1 \\
3 & 1
\end{array}\right]\)
Answer:
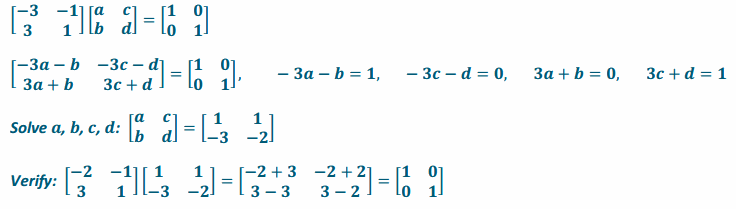
c. \(\left[\begin{array}{cc}
3 & -3 \\
-2 & 2
\end{array}\right]\)
Answer:
The determinant is 0; therefore, there is no inverse matrix.
d. \(\left[\begin{array}{cc}
0 & 1 \\
-1 & 3
\end{array}\right]\)
Answer:
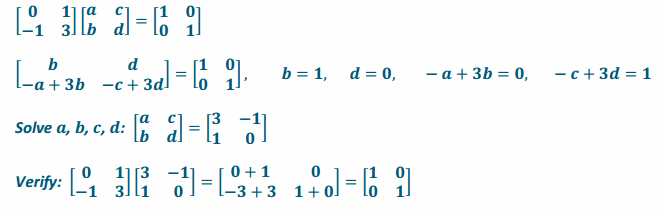
e. \(\left[\begin{array}{ll}
4 & 1 \\
2 & 1
\end{array}\right]\)
Answer:
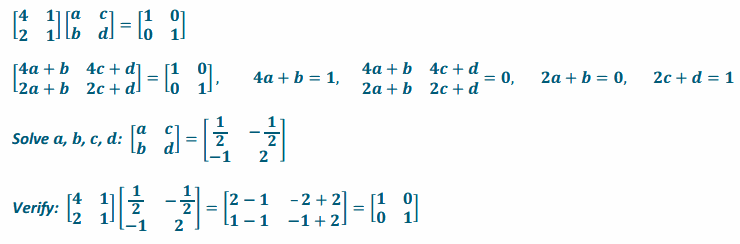
Question 3.
Find the starting point \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) if:
a. The point \(\left[\begin{array}{l}
4 \\
2
\end{array}\right]\) is the image of a pure dilation with a factor of 2.
Answer:
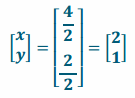
b. The point \(\left[\begin{array}{l}
4 \\
2
\end{array}\right]\) is the image of a pure dilation with a factor of \(\frac{1}{2}\).
Answer:
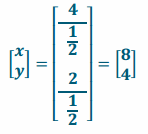
c. The point \(\left[\begin{array}{c}
-10 \\
35
\end{array}\right]\) is the image of a pure dilation with a factor of 5.
Answer:
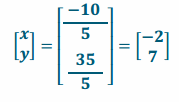
d. The point \(\left[\begin{array}{c}
\frac{4}{9} \\
\frac{16}{21}
\end{array}\right]\) is the image of a pure dilation with a factor of \(\frac{2}{3}\).
Answer:
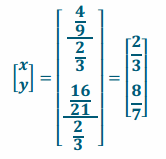
Question 4.
Find the starting point if:
a. 3+2i is the image of a reflection about the real axis.
Answer:
\(\overline{\boldsymbol{Z}}\)=3-2i
b. 3+2i is the image of a reflection about the imaginary axis.
Answer:
![]()
c. 3+2i is the image of a reflection about the real axis and then the imaginary axis.
Answer:
![]()
d. -3-2i is the image of a π radians counterclockwise rotation.
Answer:
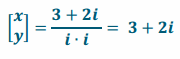
Question 5.
Let’s call the pure counterclockwise rotation of the matrix \(\left[\begin{array}{cc}
\cos (\theta) & -\sin (\theta) \\
\sin (\theta) & \cos (\theta)
\end{array}\right]\) as Rθ, and the “undo” of the pure rotation is \(\left[\begin{array}{cc}
\cos (-\theta) & -\sin (-\theta) \\
\sin (-\theta) & \cos (-\theta)
\end{array}\right]\) as Rθ.
a. Simplify \(\left[\begin{array}{cc}
\cos (-\theta) & -\sin (-\theta) \\
\sin (-\theta) & \cos (-\theta)
\end{array}\right]\).
Answer:
\(\left[\begin{array}{cc}
\cos (-\theta) & -\sin (-\theta) \\
\sin (-\theta) & \cos (-\theta)
\end{array}\right]\) = \(\left[\begin{array}{cc}
\cos (\theta) & \sin (\theta) \\
-\sin (\theta) & \cos (\theta)
\end{array}\right]\)
b. What would you get if you multiply Rθ to Rθ?
Answer:
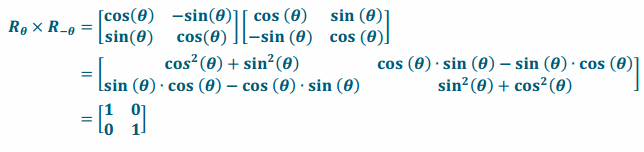
c. Write the matrix if you want to rotate \(\frac{\pi}{2}\) radians counterclockwise.
Answer:
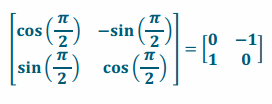
d. Write the matrix if you want to rotate \(\frac{\pi}{2}\) radians clockwise.
Answer:
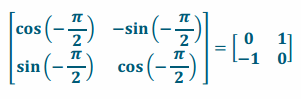
e. Write the matrix if you want to rotate \(\frac{\pi}{6}\) radians counterclockwise.
Answer:
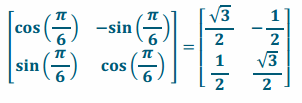
f. Write the matrix if you want to rotate \(\frac{\pi}{4}\) radians counterclockwise.
Answer:
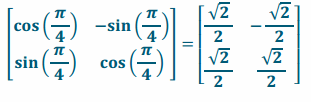
g. If the point \(\left[\begin{array}{l}
0 \\
2
\end{array}\right]\) is the image of \(\frac{\pi}{4}\) radians counterclockwise rotation, find the starting point \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\).
Answer:
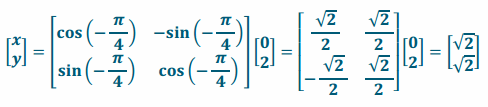
h. If the point \(\left[\begin{array}{l}
\frac{1}{2} \\
\frac{\sqrt{3}}{2}
\end{array}\right]\) is the image of \(\frac{\pi}{6}\) radians counterclockwise rotation, find the starting point \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\).
Answer:
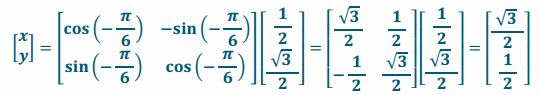
Eureka Math Precalculus Module 1 Lesson 28 Exit Ticket Answer Key
A = \(\left[\begin{array}{cc}
4 & -2 \\
-1 & 3
\end{array}\right]\) B = \(\left[\begin{array}{ll}
3 & 2 \\
1 & 4
\end{array}\right]\)
Question 1.
Is matrix A the inverse of matrix B? Show your work, and explain your answer.
Answer:
No, the product of the two matrices is not the identity matrix.
\(\left[\begin{array}{cc}
4 & -2 \\
-1 & 3
\end{array}\right]\left[\begin{array}{ll}
3 & 2 \\
1 & 4
\end{array}\right]\) = \(\left[\begin{array}{cc}
10 & 0 \\
0 & 10
\end{array}\right]\)
Question 2.
What is the determinant of matrix B? Of matrix A?
Answer:
The determinant of matrix A=|(4)(3)-(-2)(-1)|=10.
The determinant of matrix B=|(3)(4)-(2)(1)|=10.