Engage NY Eureka Math Precalculus Module 1 Lesson 30 Answer Key
Eureka Math Precalculus Module 1 Lesson 30 Example Answer Key
Example
Given \(\left[\begin{array}{cc}
\frac{1}{2} & -\frac{\sqrt{3}}{2} \\
\frac{\sqrt{3}}{2} & \frac{1}{2}
\end{array}\right]\)
a. Perform this transformation on the unit square, and sketch the results on graph paper. Label the vertices.
Answer:
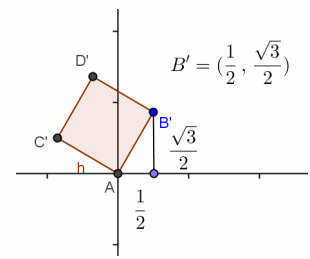
See diagram at right.
b. Explain the transformation that occurred to the unit square.
Answer:
The transformation is a 60° rotation counterclockwise about the origin.
c. Find the area of the image.
Answer:
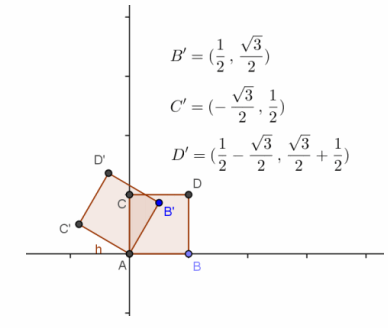
The area is 1 units2.
d. Find the inverse of this transformation.
Answer:
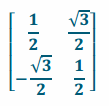
e. Explain the meaning of the inverse transformation on the unit square.
Answer:
The inverse is a -60° rotation counterclockwise about the origin.
Eureka Math Precalculus Module 1 Lesson 30 Exercise Answer Key
Opening Exercise
a. What is the geometric effect of the following matrices?
i. \(\left[\begin{array}{ll}
\boldsymbol{k} & \mathbf{0} \\
\mathbf{0} & \boldsymbol{k}
\end{array}\right]\)
Answer:
A pure dilation with a scale factor of k
ii. \(\left[\begin{array}{cc}
a & -b \\
b & a
\end{array}\right]\)
Answer:
A pure rotation
iii. \(\left[\begin{array}{cc}
\cos (\theta) & -\sin (\theta) \\
\sin (\theta) & \cos (\theta)
\end{array}\right]\)
Answer:
A pure rotation θ° counterclockwise
b. Jadavis says that the identity matrix is \(\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\). Sophie disagrees and states that the identity matrix is \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\).
i. Their teacher, Mr. Kuzy, says they are both correct and asks them to explain their thinking about matrices to each other but to also use a similar example in the real number system. Can you state each of their arguments?
Answer:
Jadavis says that any matrix added to the matrix \(\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\) does not change. This matrix is similar to 0 in the real number system, so it is the additive identity matrix.
Sophie explains that when a matrix is multiplied by \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\), the matrix does not change, just like the number 1 in the real number system; so, this matrix is the multiplicative identity.
ii. Mr. Kuzy then asks each of them to explain the geometric effect that their matrix would have on the unit square.
Answer:
\(\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\) would collapse the entire square to (0,0).
\(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) would have no effect on the unit square.
c. Given the matrices below, answer the following:
A= \(\left[\begin{array}{ll}
2 & 3 \\
1 & 4
\end{array}\right]\) B= \(\left[\begin{array}{cc}
5 & 2 \\
10 & 4
\end{array}\right]\)
i. Which matrix does not have an inverse? Explain algebraically and geometrically how you know.
Answer:
Matrix B does not have an inverse. The determinant is 0, which means it would transform the unit square to a straight line with no area.
ii. If a matrix has an inverse, find it.
Answer:
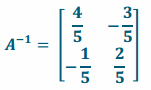
Exercises
Exercise 1.
Given \(\left[\begin{array}{ll}
\frac{1}{2} & 0 \\
0 & \frac{1}{2}
\end{array}\right]\)
a. Perform this transformation on the unit square, and sketch the results on graph paper. Label the vertices.
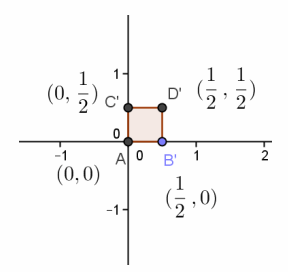
b. Explain the transformation that occurred to the unit square.
Answer:
The transformation is a dilation with a scale factor of \(\frac{1}{2}\).
c. Find the area of the image.
Answer:
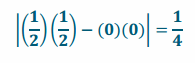
The area is \(\frac{1}{4}\) units2.
d. Find the inverse of this transformation.
Answer:
\(\left[\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right]\)
e. Explain the meaning of the inverse transformation on the unit square.
Answer:
The inverse is a dilation with a scale factor of 2.
f. If any matrix produces a dilation with a scale factor of k, what would the inverse matrix produce?
Answer:
It would produce a dilation with a scale factor of \(\frac{1}{k}\).
Exercise 2.
Given \(\left[\begin{array}{ll}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{array}\right]\)
a. Perform this transformation on the unit square, and sketch the results on graph paper. Label the vertices.
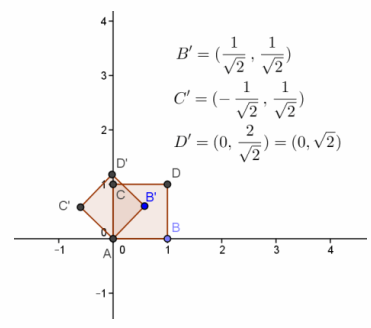
b. Explain the transformation that occurred to the unit square.
Answer:
The transformation is a 45° rotation counterclockwise about the origin.
c. Find the area of the image.
Answer:
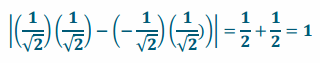
The area is 1units2.
d. Find the inverse of the transformation.
Answer:
\(\left[\begin{array}{cc}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{array}\right]\)
e. Explain the meaning of the inverse transformation on the unit square.
Answer:
The inverse is a -45° rotation counterclockwise about the origin.
f. Rewrite the original matrix if it also included a dilation with a scale factor of 2.
Answer:
\(\left[\begin{array}{ll}
\frac{2}{\sqrt{2}} & -\frac{2}{\sqrt{2}} \\
\frac{2}{\sqrt{2}} & \frac{2}{\sqrt{2}}
\end{array}\right]\) or \(\left[\begin{array}{cc}
\sqrt{2} & -\sqrt{2} \\
\sqrt{2} & \sqrt{2}
\end{array}\right]\)
g. What is the inverse of this matrix?
Answer:
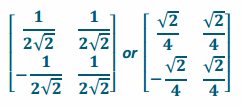
Exercise 3.
Find a transformation that would create a 90° counterclockwise rotation about the origin. Set up a system of equations, and solve to find the matrix.
Answer:
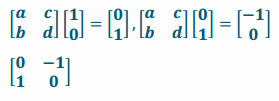
Exercise 4.
a. Find a transformation that would create a 180° counterclockwise rotation about the origin. Set up a system of equations, and solve to find the matrix.
Answer:
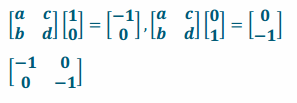
b. Rewrite the matrix to also include a dilation with a scale factor of 5.
Answer:
\(\left[\begin{array}{cc}
-5 & 0 \\
0 & -5
\end{array}\right]\)
Exercise 5.
For which values of a does \(\left[\begin{array}{cc}
3 & -100 \\
900 & a
\end{array}\right]\) have an inverse matrix?
Answer:
3a-(-100)(900)≠0
3a+90000 ≠0
a≠-30000
Exercise 6.
For which values of a does \(\left[\begin{array}{cc}
a & a+4 \\
2 & a
\end{array}\right]\) have an inverse matrix?
Answer:
(a)(a)-(a+4)(2)≠0
a2-2a-8 ≠0
(a-4)(a+2)≠0
a≠4,a≠-2
Exercise 7.
For which values of a does \(\left[\begin{array}{ll}
a+2 & a-4 \\
a-3 & a+3
\end{array}\right]\) have an inverse matrix?
Answer:
(a+2)(a+3)-(a-4)(a-3)≠0
(a2+5a+6)-(a2-7a+12) ≠0
12a-6≠0
a≠\(\frac{1}{2}\)
Exercise 8.
Chethan says that the matrix \(\left[\begin{array}{cc}
\cos \left(\theta^{\circ}\right) & -\sin \left(\theta^{\circ}\right) \\
\sin \left(\theta^{\circ}\right) & \cos \left(\theta^{\circ}\right)
\end{array}\right]\) produces a rotation θ° counterclockwise. He justifies his work by showing that when θ=60, the rotation matrix is 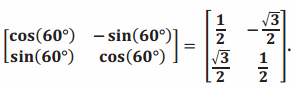 . Shayla disagrees and says that the matrix \(\left[\begin{array}{cc}
. Shayla disagrees and says that the matrix \(\left[\begin{array}{cc}
1 & -\sqrt{3} \\
\sqrt{3} & 1
\end{array}\right]\) produces a 60° rotation counterclockwise. Tyler says that he has found that the matrix \(\left[\begin{array}{cc}
2 & -2 \sqrt{3} \\
2 \sqrt{3} & 2
\end{array}\right]\) produces a 60° rotation counterclockwise, too.
a. Who is correct? Explain.
Answer:
They are all correct. All of the matrices produce a 60° rotation counterclockwise, but each has a different scale factor.
b. Which matrix has the largest scale factor? Explain.
Answer:
\(\left[\begin{array}{cc}
2 & -2 \sqrt{3} \\
2 \sqrt{3} & 2
\end{array}\right]\) has the largest scale factor of 4. The first matrix has a scale factor of 1, and the second matrix a scale factor of 2.
c. Create a matrix with a scale factor less than 1 that would produce the same rotation.
Answer:
Answers will vary. \(\left[\begin{array}{cc}
\frac{1}{4} & -\frac{\sqrt{3}}{4} \\
\frac{\sqrt{3}}{4} & \frac{1}{4}
\end{array}\right]\) would have a scale factor of \(\frac{1}{2}\).
Eureka Math Precalculus Module 1 Lesson 30 Exit Ticket Answer Key
A and B are 2×2 matrices. I is the 2×2 multiplicative identity matrix.
Question 1.
If AB=A, name the matrix represented by B.
Answer:
B= \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Question 2.
If A+B=A, name the matrix represented by B.
Answer:
B= \(\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)
Question 3.
If AB=I, name the matrix represented by B.
Answer:
B must be the inverse matrix of A.
Question 4.
Do the matrices have inverses? Justify your answer.
a. \(\left[\begin{array}{ll}
-2 & 6 \\
-3 & 9
\end{array}\right]\)
No. The determinant (-2)(9)-(6)(-3)=0.
b. \(\left[\begin{array}{cc}
-2 & 6 \\
3 & 9
\end{array}\right]\)
Yes. The determinant (-2)(9)-(6)(3)≠0.
Question 5.
Find a value of a, such that the given matrix has an inverse.
a. \(\left[\begin{array}{cc}
-4 & 3 a \\
2 & 9
\end{array}\right]\)
Answer:
(-4)(9)-(3a)(2)≠0
-36-6a ≠0
a≠-6
b. \(\left[\begin{array}{cc}
5 & a \\
-a & 5
\end{array}\right]\)
Answer:
(5)(5)-(a)(-a)≠0
25+a2≠0
For all real values of a
Eureka Math Precalculus Module 1 Lesson 30 Problem Set Answer Key
The first seven problems are more procedural. Assign problems based on student abilities. All students do not have to complete all problems.
Question 1.
Find a transformation that would create a 30° counterclockwise rotation about the origin and then its inverse.
Answer:
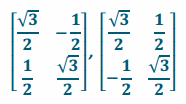
Question 2.
Find a transformation that would create a 30° counterclockwise rotation about the origin, a dilation with a scale factor of 4, and then its inverse.
Answer:
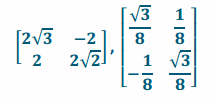
Question 3.
Find a transformation that would create a 270° counterclockwise rotation about the origin. Set up a system of equations, and solve to find the matrix.
Answer:
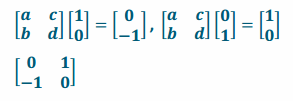
Question 4.
Find a transformation that would create a 270° counterclockwise rotation about the origin, a dilation with a scale factor of 3, and its inverse.
Answer:
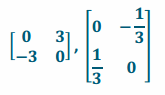
Question 5.
For which values of a does \(\left[\begin{array}{ll}
8 & a \\
a & 2
\end{array}\right]\) have an inverse matrix?
Answer:
(8)(2)-(a)(a)≠0
16-a2 ≠0
(4-a)(4+a)≠0
a≠4,a≠-4
Question 6.
For which values of a does \(\left[\begin{array}{cc}
a & a-4 \\
a+4 & a
\end{array}\right]\) have an inverse matrix?
Answer:
(a)(a)-(a-4)(a+4)≠0
a2-(a2-16) ≠0
16≠0
All real values of a will produce an inverse matrix.
Question 7.
For which values of a does \(\left[\begin{array}{cc}
3 a & 2 a-6 \\
6 a & 4 a-12
\end{array}\right]\) have an inverse matrix?
Answer:
(3a)(4a-12)-(2a-6)(6a)≠0
(12a2-36a)-(12a2-36a) ≠0
0≠0
No real values of a will produce an inverse matrix.
Question 8.
In Lesson 27, we learned the effect of a transformation on a unit square by multiplying a matrix. For example,
![]()
a. Sasha says that we can multiply the inverse of A to those resultants of the square after the transformation to get back to the unit square. Is her conjecture correct? Justify your answer.
Answer:
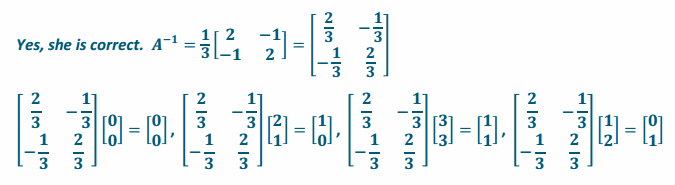
b. From part (a), what would you say about the inverse matrix with regard to the geometric effect of transformations?
Answer:
Multiplying the inverse matrix, A-1, will “undo” the transformation that was done by multiplying matrix A.
c. A pure rotation matrix is \(\left[\begin{array}{cc}
\cos (\theta) & -\sin (\theta) \\
\sin (\theta) & \cos (\theta)
\end{array}\right]\). Prove the inverse matrix for a pure rotation of \(\frac{\pi}{4}\) radians counterclockwise is \(\left[\begin{array}{cc}
\cos \left(-\frac{\pi}{4}\right) & -\sin \left(-\frac{\pi}{4}\right) \\
\sin \left(-\frac{\pi}{4}\right) & \cos \left(-\frac{\pi}{4}\right)
\end{array}\right]\), which is the same as \(\left[\begin{array}{ll}
\frac{d}{a d-b c} & \frac{-c}{a d-b c} \\
\frac{-b}{a d-b c} & \frac{d}{a d-b c}
\end{array}\right]\).
Answer:

d. Prove that the inverse matrix of a pure dilation with a factor of 4 is \(\left[\begin{array}{ll}
\frac{1}{4} & 0 \\
0 & \frac{1}{4}
\end{array}\right]\), which is the same as \(\left[\begin{array}{ll}
\frac{d}{a d-b c} & \frac{-c}{a d-b c} \\
\frac{-b}{a d-b c} & \frac{d}{a d-b c}
\end{array}\right]\).
Answer:
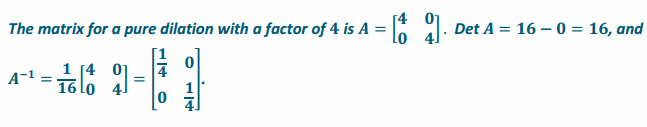
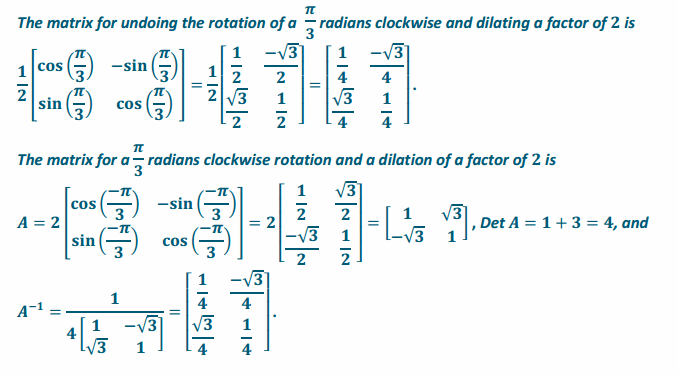
e. Prove that the matrix used to undo a \(\frac{\pi}{3}\) radians clockwise rotation and a dilation of a factor of 2 is \(\frac{1}{2}\) \(\left[\begin{array}{ll}
\cos \left(\frac{\pi}{3}\right) & -\sin \left(\frac{\pi}{3}\right) \\
\sin \left(\frac{\pi}{3}\right) & \cos \left(\frac{\pi}{3}\right)
\end{array}\right]\), which is the same as \(\left[\begin{array}{ll}
\frac{d}{a d-b c} & \frac{-c}{a d-b c} \\
\frac{-b}{a d-b c} & \frac{d}{a d-b c}
\end{array}\right]\).
Answer:
f. Prove that any matrix whose determinant is not 0 will have an inverse matrix to “undo” a transformation. For example, use the matrix A=\(\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\) and the point \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\).
Answer:
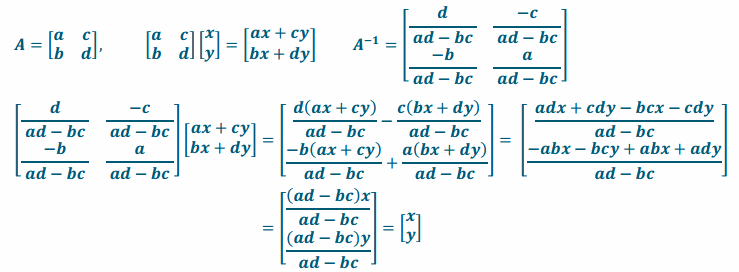
Question 9.
Perform the transformation \(\left[\begin{array}{ll}
2 & 2 \\
2 & 2
\end{array}\right]\) on the unit square.
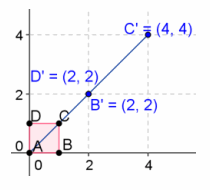
a. Can you find the inverse matrix that will “undo” the transformation? Explain your reasons arithmetically.
Answer:
No. The determinant of the matrix is 0. Therefore, there is no inverse matrix that can be found to undo the transformation.
b. When all four vertices of the unit square are transformed and collapsed onto a straight line, what can be said about the inverse?
Answer:
The determinant of the matrix is 0.
c. Find the equation of the line that all four vertices of the unit square collapsed onto.
Answer:
y=x
d. Find the equation of the line that all four vertices of the unit square collapsed onto using the matrix \(\left[\begin{array}{ll}
1 & 3 \\
2 & 6
\end{array}\right]\).
Answer:
y=2x
e. A function has an inverse function if and only if it is a one-to-one function. By applying this concept, explain why we do not have an inverse matrix when the transformation is collapsed onto a straight line.
Answer:
When doing transformations, we are mapping the four vertices to new coordinates; however, when we reverse this process, there should be a one-to-one property. However, we see that the point \(\left(\begin{array}{l}
2 \\
2
\end{array}\right)\) will map onto two different points. Because there is no one-to-one property, this means there is no inverse matrix.
Question 10.
The determinants of the following matrices are 0. Describe what pattern you can find among them.
a. 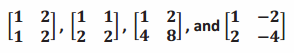
Answer:
If one column is the multiple of the other column, or one row is the multiple of the other row, then the determinant is 0, and there is no inverse matrix.
b. 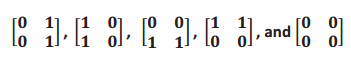
Answer:
If either column or row is 0, then the determinant is 0, and there is no inverse matrix.