Engage NY Eureka Math Precalculus Module 1 Lesson 8 Answer Key
Eureka Math Precalculus Module 1 Lesson 8 Example Answer Key
Example
\(\frac{2-6 i}{2+5 i}\)
Answer:
\(\frac{-26-22 i}{29}\)
→ In this example, we are going to divide these two complex numbers. Complex number division is different from real number division, and the quotient also looks different.
→ To divide complex numbers, we want to make the denominator a real number. We need to multiply the denominator by a complex number that makes it a real number. Multiply the denominator by its conjugate. What type of product do you get?
→ (2+5i)(2-5i)=4-10i+10i-25i2=4+25=29
You get a real number.
→ The result of multiplying a complex number by its conjugate is always a real number.
→ The goal is to rewrite this expression \(\frac{2-6 i}{2+5 i}\) as an equivalent expression with a denominator that is a real number. We now know that we must multiply the denominator by its conjugate. What about the numerator? What must we multiply the numerator by in order to obtain an equivalent expression?
→ We must multiply the numerator by the same expression, 2-5i.
→ Perform that operation, and check your answer with a neighbor.
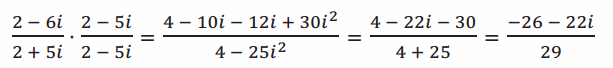
→ Tell your neighbor how to divide complex numbers.
→ Multiply the numerator and denominator by the conjugate of the denominator.
Eureka Math Precalculus Module 1 Lesson 8 Exercise Answer Key
Opening Exercise
Use the general formula to find the multiplicative inverse of each complex number.
a. 2+3i
Answer:
\(\frac{2-3 i}{13}\)
b. -7-4i
Answer:
\(\frac{-7+4 i}{65}\)
c. -4+5i
Answer:
\(\frac{-4-5 i}{41}\)
Exercises 1–11
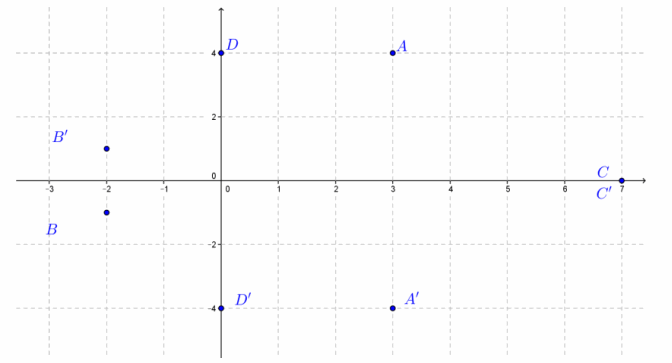
Find the conjugate, and plot the complex number and its conjugate in the complex plane. Label the conjugate with a prime symbol.
Exercise 1.
A: 3+4i
Answer:
A’: 3-4i
Exercise 2.
B: -2-i
Answer:
B’: -2+i
Exercise 3.
C: 7
Answer:
C’: 7
Exercise 4.
D: 4i
Answer:
D’: -4i
Find the modulus.
Exercise 5.
3+4i
Answer:
\(\sqrt{3^{2}+4^{2}}\)=\(\sqrt{25}\)=5
Exercise 6.
-2-i
Answer:
\(\sqrt{(-2)^{2}+(-1)^{2}}\) = \(\sqrt{5}\)
Exercise 7.
7
Answer:
\(\sqrt{7^{2}+0^{2}}\)=\(\sqrt{49}\)=7
Exercise 8.
4i
Answer:
\(\sqrt{0^{2}+(4)^{2}}\) = \(\sqrt{16}\) =4
Given z=a+bi.
Exercise 9.
Show that for all complex numbers z, |iz|=|z|.
Answer:
|iz|=|i(a+bi)|=|ai-b|=|-b+ai|=\(\sqrt{(-b)^{2}+a^{2}}\)=\(\sqrt{a^{2}+b^{2}}\)=|z|
Exercise 10.
Show that for all complex numbers z, z∙\(\overline{\boldsymbol{z}}\)=|z|2.
Answer:
z∙\(\overline{\boldsymbol{z}}\)=(a+bi)(a-bi)=a2+b2
|z|2=(√(a2+b2 ))2=a2+b2
z∙\(\overline{\boldsymbol{z}}\)=|z|2
Exercise 11.
Explain the following: Every nonzero complex number z has a multiplicative inverse. It is given by \(\frac{1}{z}\)= \(\frac{\overline{\boldsymbol{Z}}}{|\mathbf{Z}|}\).
Answer:
The multiplicative inverse of a+bi=\(\frac{a-b i}{a^{2}+b^{2}}\)=\(\frac{\overline{\mathbf{z}}}{|\mathbf{z}|}\).
Exercise 12.
Divide.
\(\frac{3+2 i}{-2-7 i}\)
Answer:
\(\frac{3+2 i}{-2-7 i}\) ∙ \(\frac{-2+7 i}{-2+7 i}\)=\(\frac{-6+21 i-4 i-14}{4+49}\)=\(\frac{-20+17 i}{53}\)
Exercise 13.
\(\frac{3}{3-i}\)
Answer:
\(\frac{3}{3-i}\)∙\(\frac{3+i}{3+i}\)=\(\frac{9+3 i}{9+1}\)=\(\frac{9+3 i}{10}\)
Eureka Math Precalculus Module 1 Lesson 8 Problem Set Answer Key
Problems 1–3 are easy problems and allow students to practice finding the conjugate and modulus and dividing complex numbers. Problems 4–6 are more difficult. Students can use examples or a geometrical approach to explain their reasoning. Problem 5 is a preview of the effect of adding or subtracting complex numbers in terms of geometrical interpretations. Students need to find and compare the modulus, rn, and φn in order to come to their assumptions.
Question 1.
Let z=4-3i and w=2-i. Show that
a. |z|=|\(\overline{\boldsymbol{z}}\) |
Answer:
|z|=\(\sqrt{(4)^{2}+(-3)^{3}}\)=\(\sqrt{16+9}\)=\(\sqrt{25}\)=5
\(\overline{\boldsymbol{z}}\)=4+3i,|\(\overline{\boldsymbol{z}}\) |=\(\sqrt{(4)^{2}+(3)^{2}}\)=\(\sqrt{16+9}\)=\(\sqrt{25}\)=5
Therefore, |z|=|\(\overline{\boldsymbol{z}}\) |.
b. |\(\frac{1}{z}\)|=\(\frac{1}{|\bar{Z}|}\)
Answer:
\(\frac{1}{z}\)=\(\frac{1}{4-3 i}\) =\(\frac{(4+3 i)}{(4-3 i)(4+3 i)}\)=\(\frac{4}{25}\)+\(\frac{3}{25}\)i; therefore,
|\(\frac{1}{z}\)|=\(\sqrt{\frac{16}{(25)^{2}}+\frac{9}{(25)^{2}}}\)=\(\sqrt{\frac{25}{(25)^{2}}}\)=\(\sqrt{\frac{25}{(25)^{2}}}\) = \(\frac{1}{5}\)
Since |\(\overline{\boldsymbol{z}}\) |=5; therefore, \(\frac{\mathbf{1}}{|\overline{\mathbf{z}}|}\) =\(\frac{1}{5}\), which equals |\(\frac{1}{z}\)|=\(\frac{1}{5}\).
c. If |z|=0, must it be that z=0?
Answer:
Yes. Let z=a+bi, and then |z|=\(\sqrt{(\boldsymbol{a})^{2}+(\boldsymbol{b})^{2}}\). If |z|=0, it indicates that \(\sqrt{(\boldsymbol{a})^{2}+(\boldsymbol{b})^{2}}\)=0. Since (a)2+(b)2 both are positive real numbers, the only values of a and b that will make the equation true is that a and b have to be 0, which means z=0+0i=0.
d. Give a specific example to show that |z+w| usually does not equal |z|+|w|.
Answer:
Answers vary, but z=3+2i and w=3-2i will work.
z+w=6+0i
|z+w|=\(\sqrt{(6)^{2}+(0)^{2}}\)=6
|z|+|w|=\(\sqrt{(3)^{2}+(2)^{2}}\)+\(\sqrt{(3)^{2}+(-2)^{2}}\)=\(2 \sqrt{13}\), which is not equal to 6.
Question 2.
Divide.
a. \(\frac{1-2 i}{2 i}\)
Answer:
\(\frac{(1-2 i)(i)}{2 i(i)}\) = \(\frac{2+i}{-2}\) or -1 – \(\frac{1}{2}\)i
b. \(\frac{5-2 i}{5+2 i}\)
Answer:
\(\frac{(5-2 i)(5-2 i)}{(5+2 i)(5-2 i)}\) = \(\frac{25-20 i-4}{25+4}\) = \(\frac{21-20 i}{29}\) or \(\frac{21}{29}\) – \(\frac{20}{29}\)i
c. \(\frac{\sqrt{3}-2 i}{-2-\sqrt{3} i}\)
Answer:
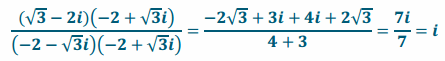
Question 3.
Prove that |zw|=|z|∙|w| for complex numbers z and w.
Answer:
Since |z|2=z ∙ \(\overline{\boldsymbol{z}}\); therefore, |zw|2=(zw)((\(\overline{\boldsymbol{Z W}}\)) )=(zw)(\(\overline{\boldsymbol{Z W}}\) )=z\(\overline{\boldsymbol{z}}\)w\(\overline{\boldsymbol{w}}\)=|z|2∙|w|2.
Now we have |zw|2=|z|2 ∙ |w|2; therefore, |zw|=|z|∙|w|.
Question 4.
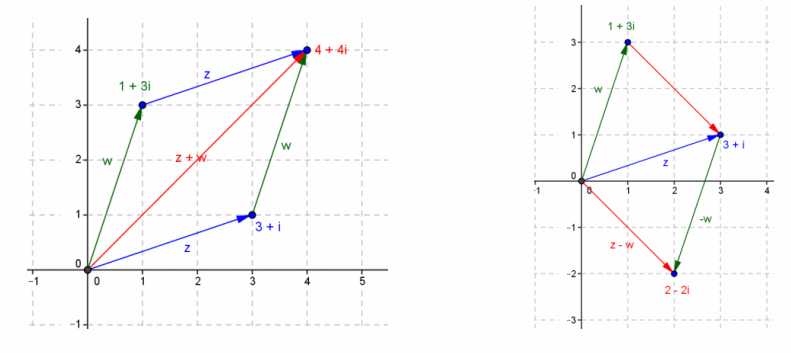
Given z=3+i, w=1+3i.
a. Find z+w, and graph z, w, and z+w on the same complex plane. Explain what you discover if you draw line segments from the origin to those points z, w, and z+w. Then, draw line segments to connect w to z + and z + w to z.
Answer:
z+w=4+4i
Students should discover that the lines form a parallelogram. They then can graphically see that the lengths of the two sides are greater than the diagonal, |z+w|≤|z|+|w|.
b. Find -w, and graph z, w, and z-w on the same complex plane. Explain what you discover if you draw line segments from the origin to those points z, w, and z-w. Then, draw line segments to connect w to z-w and z-w to z.
Answer:
z-w=2-2i
Students should discover that the lines form a parallelogram. They then can graphically see that the lengths of the two sides are greater than the diagonal, |z-w|≤|z|+|w|.
Question 5.
Explain why |z+w|≤|z|+|w| and |z-w|≤|z|+|w| geometrically. (Hint: Triangle inequality theorem)
Answer:
By using Example 5, we can apply the triangle inequality theorem into these two formulas.
Eureka Math Precalculus Module 1 Lesson 8 Exit Ticket Answer Key
Question 1.
Given z=4-3i.
a. What does \(\overline{\boldsymbol{z}}\) mean?
Answer:
\(\overline{\boldsymbol{z}}\) means the conjugate of z, which is 4+3i.
b. What does \(\overline{\boldsymbol{z}}\) do to z geometrically?
Answer:
\(\overline{\boldsymbol{z}}\) is the reflection of z across the real axis.
c. What does |z| mean both algebraically and geometrically?
Answer:
|z| is a modulus of z, which is a real number.
|z| is the distance from the point z=4-3i to the origin in the complex plane.
|z|=\(\sqrt{a^{2}+b^{2}}\)
=\(\sqrt{(4)^{2}+(-3)^{2}}\)
=\(\sqrt{16+9}\)
=\(\sqrt{25}\)
=5
Question 2.
Describe how to use the conjugate to divide 2-i by 3+2i, and then find the quotient.
Answer:
When 3+2i is multiplied by its conjugate of 3-2i, the denominator is a real number, which is necessary.
Multiply by \(\frac{3-2 i}{3-2 i}\).
\(\frac{2-i}{3+2 i}\)=\(\frac{(2-i)(3-2 i)}{(3+2 i)(3-2 i)}\)=\(\frac{6-4 i-3 i-2}{9+4}\)=\(\frac{4-7 i}{13}\)=\(\frac{4}{13}\)–\(\frac{7}{13}\)i