A Rectangle is a type of quadrilateral. In a particular condition, we can say that a rectangle is a parallelogram. In a rectangle the opposite sides are equal and the angles are 90 degrees. In this article, we are going to prove that in a rectangle the diagonals are of equal lengths. We need to prove that two line segments are of equal lengths.
Properties of a Rectangle:
1. The opposite sides are equal.
2. The diagonals in a rectangle bisect each other.
3. Any two adjacent angles are supplementary.
4. The opposite angles are equal.
Also Read:
- A Parallelogram, whose Diagonals are of Equal Length, is a Rectangle
- A Rhombus is a Parallelogram whose Diagonals Meet at Right Angles
- A Parallelogram whose Diagonals Intersect at Right Angles is a Rhombus
In a Rectangle the Diagonals are of Equal Lengths
Theorem:
Prove that the diagonals of a rectangle are of equal lengths?
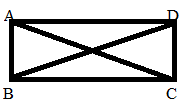
To prove: AC = BD
Let ABCD be a rectangle.
The opposite sides are of equal lengths.
We have to show that AC = BD
BC = CB [since common]
AB = DC [opposite sides of a parallelogram are equal]
ABC =DCA = 90°
so ABC ≅ DCB (SAS theorem)
Hence AC=DB
Hence Proved
Therefore we have proven that in a rectangle the diagonals are of equal lengths.
FAQs on Prove that Diagonals of a Rectangle are Equal in Length
1. How many equal-length diagonals are there in a rectangle?
A rectangle and a crossed rectangle are quadrilaterals with the following properties in common: Opposite sides are equal in length. The two diagonals are equal in length. It has two lines of reflectional symmetry and rotational symmetry of order 2.
2. Do diagonals have an equal length?
Square, Rectangle, Parallelogram have diagonals of equal length because the opposite sides of those quadrilaterals are the same.
3. Why are the diagonals of rectangles equal?
Yes, the diagonals of a rectangle are the same. This is because the two diagonals are the hypotenuse of the two right-angled triangles formed by the diagonals. The opposite sides of a rectangle are the same.