Know the indirect variation definition here. Check day-to-day usage of inverse variations and know various problems involved in it. Gather the complete material of inverse proportions or indirect proportions. Follow the step-by-step process which helps you in solving the complicated problems. Get the detailed preparation material of indirect variation and follow all the tips and tricks mentioned below. Scroll down to the below sections to know the various details like definition, word problems, examples, formulae, key ideas, tips, tricks, etc.
Also, Read:
Importance of Inverse Variation
We use variation in values of quantities in day-to-day life. In most cases, the variation of the value of some quantity depends on the value of another quantity. Inverse variation or inverse proportion is defined as the variable which varies inversely in respect to another variable.
For suppose, If the train is traveling for x distance at a constant speed, the time taken to travel x distance remains constant, if there is a change in the speed then the time taken will also change. Hence, the inverse proportion values work here.
Indirect Variation – Definition
As we know that direct variation implies the direct proportion of one quantity to another, an inverse proportion is vice-verse of direct proportion. The change in one quantity is inversely proportional to the other quantity. i.e., If there is an increase in the value of one quantity, then there will be a decrease in the value of another quantity. Thus, both the values of quantities are defined to be indirectly proportional.
Inverse Variation Equation
Quantities that are available in inverse variation are expressed as,
x ∝ 1/y
xy = k, where k is the constant of proportionality and x,y are the values of 2 quantities. To define the change in values of two quantities, suppose that the initial values are x1, y1 and the final values are x2, y2 which are in inverse variation. The equation can be expressed as,
x1/x2 = y1/y2
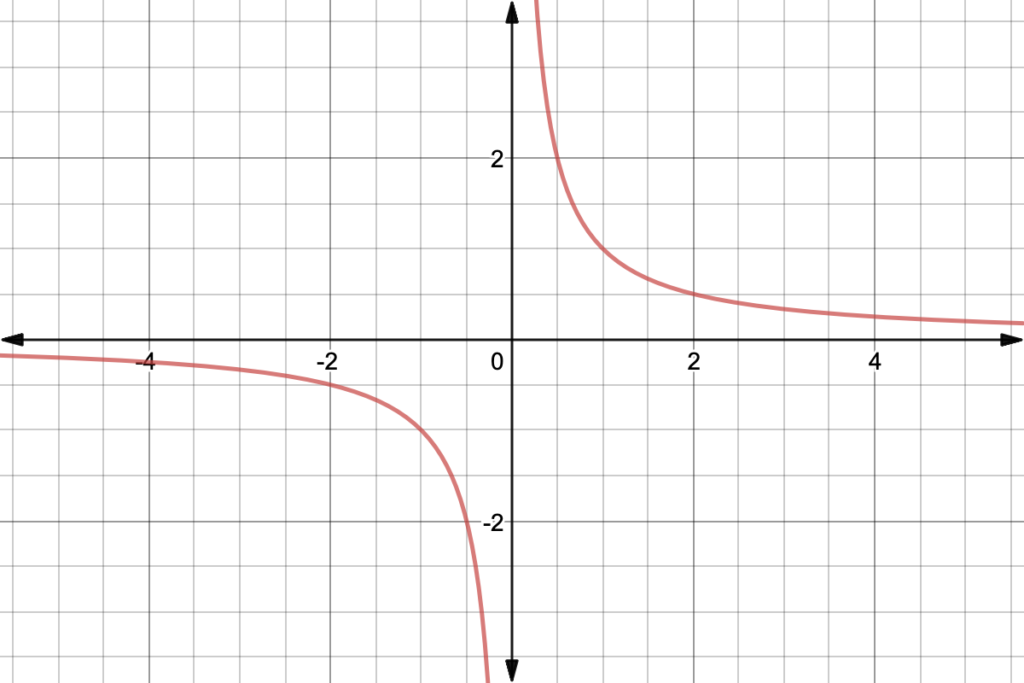
Inverse Variation Example Graph
How to Solve Inverse Variation Problems?
Go through the simple procedure listed below to solve the Problems on Inverse Variation. They are along the lines
Step 1: First of all, check the given equation. We use the formula y = k/x to solve indirect proportions. When you are working on the word problems, consider the variables given other than x and y and also use those variables which are relevant to the problem to be solved. Check all the values carefully to determine the changes in inverse variation equations like square roots, squares, and cubes.
Step 2: Find the complete information in the problem and find the “k” value which is found in step 2.
Step 3: Rewrite the resultant equation which is obtained in step 1. Substitute the value of k which we got in step 2.
Step 4: With the equation we got in step 3 and also with the help of the remaining information in the question, we find the final solution in this step. While solving the word problems, include the units in the final answer.
How to Identify Inverse Variation?
- We define it as yy inversely varies with xx if yy is defined as the product of a constant number kk and xx reciprocal
- The value of kk will never be 0(zero), i.e, k≠0
- kk is defined as the fixed or the constant product of xx and yy which means that multiplying both the values of xx and yy always gives the constant output of kk.
Inverse Variation Word Problems
Problem 1:
The number of hours constructing a deep well is inversely proportional to the number of men working doing it. It takes 10 hours for 2 men to construct. How many men are needed to complete the work in 4 hours?
Solution:
Let y be the number of men working
Let x be the number of hours
In the first case,
y = 10, x = 2
As we know the equation of inverse proportion,
yx = k
Substituting the values in the equation,
(10)(2) = k
k = 20
Therefore, the value of k = 20
In the second case,
y = ?, x = 4
As we already got the k value i.e., 20
Substitute the values in the above equation,
yx = k
(y)(4) = 20
4y = 20
y = 20/4
y = 5
Therefore, no of men required to finish the work in 4 hours = 5 men
Hence, the final solution is 5 men
Problem 2:
When riding a bus at 55km/hr average speed, it takes Marcel 3 hours to reach his destination. How long will it take him if he travels by van at 70 km/hr?
Solution:
Let y be the average speed
Let x be the number of hours
In the first case,
y = 55, x = 3
As we know the equation of inverse proportion,
yx = k
Substituting the values in the equation,
(55)(3) = k
k = 165
Therefore, the value of k is 165
In the second case,
y = 70, x = ?
As we already got the k value i.e., 165
Substitute the values in the above equation,
yx = k
70x = 165
x = 165/70
x = 2.36
Therefore, it takes 2.36 hours for him to travel by van at 70 km/hr
Thus, the final solution is 2.36 hours
Problem 3:
A group of 10 men decided to rent a house for $100 for the stay of one week. But two people of them got sick and couldn’t join them. How much would each man pay for the rent?
Solution:
Let no of men = y
Let payment of each man = x
In the first case,
y = 10
x = 10
As we know the equation of inverse proportion,
yx = k
Substituting the values in the equation,
(10)(10) = k
k = 100
Therefore, the value of k is 100
In the second case,
As 2 men dropped to join the rent, we get the value as
y = 10-2
y = 8
x =?
As we already got the k value i.e., 100
Substitute the values in the above equation,
yx = k
(8)(x) = 100
x = 100/8
x = 2.5
Therefore, each man would pay $2.5 for the rent.
Thus, the final solution is $2.5
Problem 4:
Clark on his first drive traveled from home to his destination or 6 hours with an average speed of 60 km/hr. What must be his average speed if he wants to get there within 5 hours?
Solution:
Let y be the no of hours
Let x be average speed
In the first case,
y = 6, x = 60
As we know the equation of inverse proportion,
yx = k
Substituting the values in the equation,
(6)(60) = k
k =360
In the second case,
y = 5, x = ?
As we already got the k value i.e., 360
Substitute the values in the above equation,
yx = k
(5)(x) = 360
x = 360/5
x = 72 km/hr
Therefore, he must maintain an average speed of 72km/hr to get there within 5 hours
Problem 5:
Three fishermen decided to contribute individually to purchase a boat worth $1500. They decided to let other fishermen join them so they can lower their payments. How many fishermen will they need so that each one will pay $300?
Solution:
Let y be the no of fishermen
Let x be the amount to be paid by each fisherman
In the first case,
y = 3, x = 1500/3 = 500
As we know the equation of inverse proportion,
yx = k
Substituting the values in the equation,
(3)(500) = k
k = 1500
Therefore, the value of k = 1500
In the second case,
y = ?, x = 300
As we already got the k value i.e., 1500
Substitute the values in the above equation,
yx = k
(y)(300) = 1500
y = 1500/300
y = 5
Therefore, they need 5 fishermen that each one will pay $300
Problem 6:
The volume of a gas t constant temperature varies inversely as the pressure. The volume of the gas is 75 milliliters when the pressure is 1.5 atmospheres. Find the volume of the gas when the pressure is increased to 2.5 atmospheres?
Solution:
Let the volume of gas be V
Let the pressure be P
As we know the equation,
V = k/P
75 = k/1.5
112.5 = k
The value of k is 112.5
Substitute the value of k in the above equation
V = 112.5/P
V = 112.5/2.5
V = 45 milliliters
Therefore, the volume of the gas is 45 milliliters when the pressure is increased to 2.5 atmospheres
Problem 7:
The bases of triangles having equal areas are inversely proportional to their altitudes. The base of a certain triangle is 24 cm and its altitude is 30 cm. Find the base of the triangle whose altitude is 40 cm?
Solution:
Let b be the bases of the triangle
Let a be the altitudes of the triangle
As we know the equation of inverse proportion
b = k/a
(24) = k/(30)
(30)(24) = k
k = 720
Therefore, the value of k is 720
Substitute the value of k and a in the equation,
b = 720/40
b = 18 cm
Therefore, the base of the triangle is 18 cm
Thus the final solution is 18 cm
Problem 8:
The number of hours required to do a job varies inversely as the number of people working together. If it takes 8 hours or 5 people to paint a house how long will it take 12 people to paint the house?
Solution:
Let h be the number of hours
Let p be the number of people
As we know the equation of inverse proportion
h = k/p
(8) = k/(5)
(5)(8) = k
k = 40
Substitute the value of k and p in the above equation
h = 40/12
h = 10/3
h ≡ 3.33 hours
Therefore, it takes 3.33 hours for 12 people to paint the house.