This handy Spectrum Math Grade 7 Answer Key Chapter 1 Lesson 1.7 Subtracting Fractions and Mixed Numbers provides detailed answers for the workbook questions.
Spectrum Math Grade 7 Chapter 1 Lesson 1.7 Subtracting Fractions and Mixed Numbers Answers Key
To subtract fractions or mixed numbers when the denominators are different, rename the fractions so the denominators are the same.

Subtract. Write each answer in simplest form.
Question 1.
a.
![]()
Answer: \(\frac{7}{20}\)
\(\frac{3}{5}\) – \(\frac{1}{4}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{3}{5}\) x \(\frac{4}{4}\)] – [\(\frac{1}{4}\) x \(\frac{5}{5}\)]
= \(\frac{12}{20}\) – \(\frac{5}{20}\)
= \(\frac{12 – 5}{20}\)
After simplification, the result is given by,
= \(\frac{7}{20}\)
b.
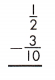
Answer: \(\frac{1}{5}\)
\(\frac{1}{2}\) – \(\frac{3}{10}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{1}{2}\) x \(\frac{10}{10}\)] – [\(\frac{3}{10}\) x \(\frac{2}{2}\)]
= \(\frac{10}{20}\) – \(\frac{6}{20}\)
= \(\frac{10 – 6}{20}\)
After simplification, the result is given by,
= \(\frac{4}{20}\)
= \(\frac{1}{5}\)
c.
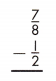
Answer: \(\frac{3}{8}\)
\(\frac{7}{8}\) – \(\frac{1}{2}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{7}{8}\) x \(\frac{2}{2}\)] – [\(\frac{1}{2}\) x \(\frac{8}{8}\)]
= \(\frac{14}{16}\) – \(\frac{8}{16}\)
= \(\frac{14 – 8}{16}\)
After simplification, the result is given by,
= \(\frac{6}{16}\)
= \(\frac{3}{8}\)
d.
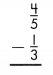
Answer: \(\frac{7}{15}\)
\(\frac{4}{5}\) – \(\frac{1}{3}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{4}{5}\) x \(\frac{3}{3}\)] – [\(\frac{1}{3}\) x \(\frac{5}{5}\)]
= \(\frac{12}{15}\) – \(\frac{5}{15}\)
= \(\frac{12 – 5}{15}\)
After simplification, the result is given by,
= \(\frac{7}{15}\)
Question 2.
a.
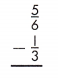
Answer: \(\frac{1}{2}\)
\(\frac{5}{6}\) – \(\frac{1}{3}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{5}{6}\) x \(\frac{3}{3}\)] – [\(\frac{1}{3}\) x \(\frac{6}{6}\)]
= \(\frac{15}{18}\) – \(\frac{6}{18}\)
= \(\frac{15 – 6}{18}\)
After simplification, the result is given by,
= \(\frac{9}{18}\)
= \(\frac{1}{2}\)
b.
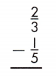
Answer: \(\frac{7}{15}\)
\(\frac{2}{3}\) – \(\frac{1}{5}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{2}{3}\) x \(\frac{5}{5}\)] – [\(\frac{1}{5}\) x \(\frac{3}{3}\)]
= \(\frac{10}{15}\) – \(\frac{3}{15}\)
= \(\frac{10 – 3}{15}\)
After simplification, the result is given by,
= \(\frac{7}{15}\)
c.
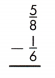
Answer: \(\frac{11}{24}\)
\(\frac{5}{8}\) – \(\frac{1}{6}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{5}{8}\) x \(\frac{6}{6}\)] – [\(\frac{1}{6}\) x \(\frac{8}{8}\)]
= \(\frac{30}{48}\) – \(\frac{8}{48}\)
= \(\frac{30 – 8}{48}\)
After simplification, the result is given by,
= \(\frac{22}{48}\)
= \(\frac{11}{24}\)
d.
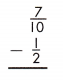
Answer: \(\frac{7}{20}\)
\(\frac{7}{10}\) – \(\frac{1}{2}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{7}{10}\) x \(\frac{2}{2}\)] – [\(\frac{1}{2}\) x \(\frac{7}{10}\)]
= \(\frac{14}{20}\) – \(\frac{7}{20}\)
= \(\frac{14 – 7}{20}\)
After simplification, the result is given by,
= \(\frac{7}{20}\)
Question 3.
a.
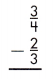
Answer: \(\frac{1}{12}\)
\(\frac{3}{4}\) – \(\frac{2}{3}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{3}{4}\) x \(\frac{3}{3}\)] – [\(\frac{2}{3}\) x \(\frac{4}{4}\)]
= \(\frac{9}{12}\) – \(\frac{8}{12}\)
= \(\frac{9 – 8}{12}\)
After simplification, the result is given by,
= \(\frac{1}{12}\)
b.
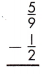
Answer: \(\frac{1}{18}\)
\(\frac{5}{9}\) – \(\frac{1}{2}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{5}{9}\) x \(\frac{2}{2}\)] – [\(\frac{1}{2}\) x \(\frac{9}{9}\)]
= \(\frac{10}{18}\) – \(\frac{9}{18}\)
= \(\frac{10 – 9}{18}\)
After simplification, the result is given by,
= \(\frac{1}{18}\)
c.
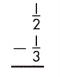
Answer: \(\frac{1}{6}\)
\(\frac{1}{2}\) – \(\frac{1}{3}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{1}{2}\) x \(\frac{3}{3}\)] – [\(\frac{1}{3}\) x \(\frac{2}{2}\)]
= \(\frac{3}{6}\) – \(\frac{2}{6}\)
= \(\frac{3 – 2}{6}\)
After simplification, the result is given by,
= \(\frac{1}{6}\)
d.
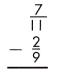
Answer: \(\frac{41}{99}\)
\(\frac{7}{11}\) – \(\frac{2}{9}\)
To subtract fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= [\(\frac{7}{11}\) x \(\frac{9}{9}\)] – [\(\frac{2}{9}\) x \(\frac{11}{11}\)]
= \(\frac{63}{99}\) – \(\frac{22}{99}\)
= \(\frac{63 – 22}{99}\)
After simplification, the result is given by,
= \(\frac{41}{99}\)
Question 4.
a.
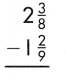
Answer: 1\(\frac{1}{8}\)
2\(\frac{3}{8}\) – 1\(\frac{2}{9}\)
Partition the fractions and whole numbers to subtract them separately.
= (2- 1) + [\(\frac{3}{8}\) – \(\frac{2}{9}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 1 + [\(\frac{3}{8}\) x \(\frac{9}{9}\)] – [\(\frac{2}{9}\) x \(\frac{8}{8}\)]
= 1 + \(\frac{27}{72}\) – \(\frac{18}{72}\)
= 1 + \(\frac{27 – 18}{72}\)
After simplification,
= 1 + \(\frac{9}{72}\)
= 1 + \(\frac{1}{8}\)
Therefore, the result is given by,
= 1\(\frac{1}{8}\)
b.
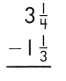
Answer: 1\(\frac{11}{12}\)
3\(\frac{1}{4}\) – 1\(\frac{1}{3}\)
Partition the fractions and whole numbers to subtract them separately.
= (3- 1) + [\(\frac{1}{4}\) – \(\frac{1}{3}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 2 + [\(\frac{1}{4}\) x \(\frac{3}{3}\)] – [\(\frac{1}{3}\) x \(\frac{4}{4}\)]
= 2 + \(\frac{3}{12}\) – \(\frac{4}{12}\)
= 1 + \(\frac{15}{12}\) – \(\frac{4}{12}\)
= 1 + \(\frac{15 – 4}{12}\)
After simplification,
= 1 + \(\frac{11}{12}\)
Therefore, the result is given by,
= 1\(\frac{11}{12}\)
c.
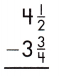
Answer: 0\(\frac{3}{4}\)
4\(\frac{1}{2}\) – 3\(\frac{3}{4}\)
Partition the fractions and whole numbers to subtract them separately.
= (4- 3) + [\(\frac{1}{2}\) – \(\frac{3}{4}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 1 + [\(\frac{1}{2}\) x \(\frac{4}{4}\)] – [\(\frac{3}{4}\) x \(\frac{2}{2}\)]
= 1 + \(\frac{4}{8}\) – \(\frac{6}{8}\)
= 0 + \(\frac{12}{8}\) – \(\frac{6}{8}\)
= 0 + \(\frac{12 – 6}{8}\)
After simplification,
= 0 + \(\frac{6}{8}\)
= 0 + \(\frac{3}{4}\)
Therefore, the result is given by,
= 0\(\frac{3}{4}\)
d.
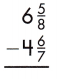
Answer: 1\(\frac{43}{56}\)
6\(\frac{5}{8}\) – 4\(\frac{6}{7}\)
Partition the fractions and whole numbers to subtract them separately.
= (6 – 4) + [\(\frac{5}{8}\) – \(\frac{6}{7}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 2 + [\(\frac{5}{8}\) x \(\frac{7}{7}\)] – [\(\frac{6}{7}\) x \(\frac{8}{8}\)]
= 2 + \(\frac{35}{56}\) – \(\frac{48}{56}\)
= 1 + \(\frac{91}{56}\) – \(\frac{48}{56}\)
= 1 + \(\frac{91 – 48}{56}\)
After simplification,
= 1 + \(\frac{43}{56}\)
Therefore, the result is given by,
= 1\(\frac{43}{56}\)
Question 5.
a.
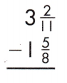
Answer: 1\(\frac{49}{88}\)
3\(\frac{2}{11}\) – 1\(\frac{5}{8}\)
Partition the fractions and whole numbers to subtract them separately.
= (3 – 1) + [\(\frac{2}{11}\) – \(\frac{5}{8}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 2 + [\(\frac{2}{11}\) x \(\frac{8}{8}\)] – [\(\frac{5}{8}\) x \(\frac{11}{11}\)]
= 2 + \(\frac{16}{88}\) – \(\frac{55}{88}\)
= 1 + \(\frac{104}{88}\) – \(\frac{55}{88}\)
= 1 + \(\frac{104 – 55}{88}\)
After simplification,
= 1 + \(\frac{49}{88}\)
Therefore, the result is given by,
= 1\(\frac{49}{88}\)
b.
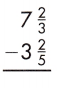
Answer: 4\(\frac{4}{15}\)
7\(\frac{2}{3}\) – 3\(\frac{2}{5}\)
Partition the fractions and whole numbers to subtract them separately.
= (7 – 3) + [\(\frac{2}{3}\) – \(\frac{2}{5}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 4 + [\(\frac{2}{3}\) x \(\frac{5}{5}\)] – [\(\frac{2}{5}\) x \(\frac{3}{3}\)]
= 4 + \(\frac{10}{15}\) – \(\frac{6}{15}\)
= 4 + \(\frac{10 – 6}{15}\)
After simplification,
= 4 + \(\frac{4}{15}\)
Therefore, the result is given by,
= 4\(\frac{4}{15}\)
c.
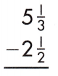
Answer: 2\(\frac{5}{6}\)
5\(\frac{1}{3}\) – 2\(\frac{1}{2}\)
Partition the fractions and whole numbers to subtract them separately.
= (5 – 2) + [\(\frac{1}{3}\) – \(\frac{1}{2}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 3 + [\(\frac{1}{3}\) x \(\frac{2}{2}\)] – [\(\frac{1}{2}\) x \(\frac{3}{3}\)]
= 3 + \(\frac{2}{6}\) – \(\frac{3}{6}\)
= 2 + \(\frac{8}{6}\) – \(\frac{3}{6}\)
= 2 + \(\frac{8 – 3}{6}\)
After simplification,
= 2 + \(\frac{5}{6}\)
Therefore, the result is given by,
= 2\(\frac{5}{6}\)
d.
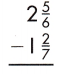
Answer: 1\(\frac{23}{42}\)
2\(\frac{5}{6}\) – 1\(\frac{2}{7}\)
Partition the fractions and whole numbers to subtract them separately.
= (2 – 1) + [\(\frac{5}{6}\) – \(\frac{2}{7}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 1 + [\(\frac{5}{6}\) x \(\frac{7}{7}\)] – [\(\frac{2}{7}\) x \(\frac{6}{6}\)]
= 1 + \(\frac{35}{42}\) – \(\frac{12}{42}\)
= 1 + \(\frac{35 – 12}{42}\)
After simplification,
= 1 + \(\frac{23}{42}\)
Therefore, the result is given by,
= 1\(\frac{23}{42}\)
Question 6.
a.
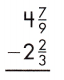
Answer: 2\(\frac{5}{9}\)
4\(\frac{7}{9}\) – 2\(\frac{2}{3}\)
Partition the fractions and whole numbers to subtract them separately.
= (4 – 2) + [\(\frac{7}{9}\) – \(\frac{2}{3}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 2 + [\(\frac{7}{9}\) x \(\frac{3}{3}\)] – [\(\frac{2}{3}\) x \(\frac{9}{9}\)]
= 2 + \(\frac{21}{27}\) – \(\frac{6}{27}\)
= 2 + \(\frac{21 – 6}{27}\)
After simplification,
= 2+ \(\frac{15}{27}\)
= 2+ \(\frac{5}{9}\)
Therefore, the result is given by,
= 2\(\frac{5}{9}\)
b.
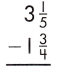
Answer: 1\(\frac{9}{20}\)
3\(\frac{1}{5}\) – 1\(\frac{3}{4}\)
Partition the fractions and whole numbers to subtract them separately.
= (3 – 1) + [\(\frac{1}{5}\) – \(\frac{3}{4}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 2 + [\(\frac{1}{5}\) x \(\frac{4}{4}\)] – [\(\frac{3}{4}\) x \(\frac{5}{5}\)]
= 2 + \(\frac{4}{20}\) – \(\frac{15}{20}\)
= 1 + \(\frac{24}{20}\) – \(\frac{15}{20}\)
= 1 + \(\frac{24 – 15}{20}\)
After simplification,
= 1+ \(\frac{9}{20}\)
Therefore, the result is given by,
= 1\(\frac{9}{20}\)
c.
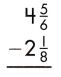
Answer: 2\(\frac{17}{24}\)
4\(\frac{5}{6}\) – 2\(\frac{1}{8}\)
Partition the fractions and whole numbers to subtract them separately.
= (4 – 2) + [\(\frac{5}{6}\) – \(\frac{1}{8}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 2 + [\(\frac{5}{6}\) x \(\frac{8}{8}\)] – [\(\frac{1}{8}\) x \(\frac{6}{6}\)]
= 2 + \(\frac{40}{48}\) – \(\frac{6}{48}\)
= 2 + \(\frac{40 – 6}{48}\)
After simplification,
= 2 + \(\frac{34}{48}\)
= 2 + \(\frac{17}{24}\)
Therefore, the result is given by,
= 2\(\frac{17}{24}\)
d.
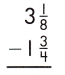
Answer:1\(\frac{1}{4}\)
3\(\frac{1}{8}\) – 1\(\frac{3}{4}\)
Partition the fractions and whole numbers to subtract them separately.
= (3 – 1) + [\(\frac{1}{8}\) – \(\frac{3}{4}\)]
To add fractions or mixed numbers when the denominators are different, rename the fractions in such a way by multiplying denominator of one fraction with another, to make the denominators same.
= 2 + [\(\frac{1}{8}\) x \(\frac{4}{4}\)] – [\(\frac{3}{4}\) x \(\frac{8}{8}\)]
= 2 + \(\frac{4}{32}\) – \(\frac{24}{32}\)
= 1 + \(\frac{36}{32}\) – \(\frac{24}{32}\)
= 1 + \(\frac{36 – 24}{48}\)
After simplification,
= 1 + \(\frac{12}{48}\)
= 1 + \(\frac{1}{4}\)
Therefore, the result is given by,
= 1\(\frac{1}{4}\)