This handy Spectrum Math Grade 7 Answer Key Chapter 4 Lesson 4.2 Testing Proportional Relationships provides detailed answers for the workbook questions.
Spectrum Math Grade 7 Chapter 4 Lesson 4.2 Testing Proportional Relationships Answers Key
Relationships are proportional if they indicate the relationship between values stays constant. Graphing values can help determine if the relationship is proportional.

Step 1: Graph each point on a grid.
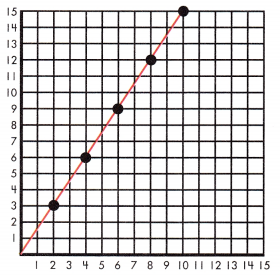
Step 2: Connect the points.
Step 3: Decide if the line is straight or not.
If the line connecting points on a grid is straight, the relationship between the quantities is proportional.
Graph the points to determine if the relationship in the table is proportional.
Question 1.
a.
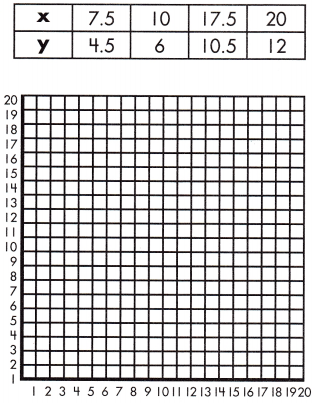
Proportional? ______
Answer: Yes
Relationships are proportional if they indicate the relationship between values stays constant. Graphing values can help determine if the relationship is proportional.
Step 1: Graph each point on a grid.
Step 2: Connect the points.
Step 3: Decide if the line is straight or not.
If the line connecting points on a grid is straight, the relationship between the quantities is proportional. Otherwise the relationship between the quantities is not proportional.
In the above graph the line is straight hence it is proportional.
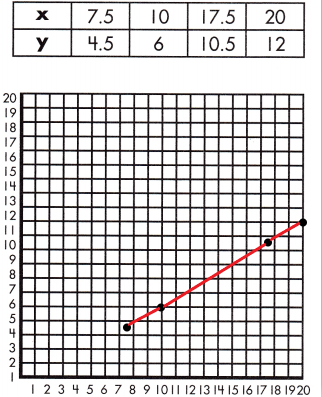
b.
Proportional? ______
Answer: No
Relationships are proportional if they indicate the relationship between values stays constant. Graphing values can help determine if the relationship is proportional.
Step 1: Graph each point on a grid.
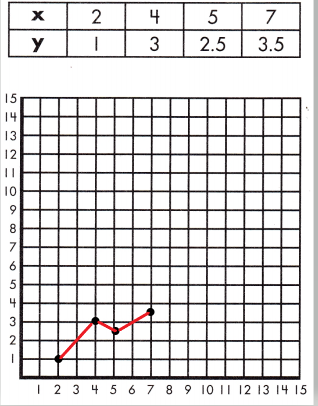
Step 2: Connect the points.
Step 3: Decide if the line is straight or not.
If the line connecting points on a grid is straight, the relationship between the quantities is proportional. Otherwise the relationship between the quantities is not proportional.
In the above graph the line is not straight hence it is not proportional.
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
A ratio can be expressed as 1 to 2, 1:2, or \(\frac{1}{2}\), and it means that for every 1 of the first item, there are 2 of the other item.
Cross-multiply to determine if two ratios are equal.
\(\frac{2}{4}\), \(\frac{3}{6}\) 2 × 6 = 12 3 × 4 = 12 \(\frac{2}{4}\) = \(\frac{3}{6}\)
Circle the ratios that are equal. Show your work.
Question 1.
a. \(\frac{1}{3}\), \(\frac{2}{6}\)
Answer: \(\frac{1}{3}\), \(\frac{2}{6}\) are equal ratios
\(\frac{1}{3}\), \(\frac{2}{6}\)
1 x 6 = 12
2 x 6 = 12
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{1}{3}\) , \(\frac{2}{6}\) are equal ratios.
b. \(\frac{3}{8}\), \(\frac{1}{4}\)
Answer: \(\frac{3}{8}\), \(\frac{1}{4}\) are not equal ratios.
\(\frac{3}{8}\), \(\frac{1}{4}\)
3 x 4 = 12
1 x 8 = 8
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{3}{8}\), \(\frac{1}{4}\) are unequal ratios.
c. \(\frac{3}{5}\), \(\frac{9}{15}\)
Answer: \(\frac{3}{5}\), \(\frac{9}{15}\) are equal ratios
\(\frac{3}{5}\), \(\frac{9}{15}\)
3 x 15 = 45
9 x 5 = 45
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{3}{5}\), \(\frac{9}{15}\) are equal ratios.
Question 2.
a. \(\frac{3}{4}\), \(\frac{9}{12}\)
Answer: \(\frac{3}{4}\), \(\frac{9}{12}\) are equal ratios
\(\frac{3}{4}\), \(\frac{9}{12}\)
3 x 12 = 36
4 x 9 = 36
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{3}{4}\), \(\frac{9}{12}\) are equal ratios.
b. \(\frac{1}{2}\), \(\frac{4}{8}\)
Answer: \(\frac{1}{2}\), \(\frac{4}{8}\) are equal ratios
\(\frac{1}{2}\), \(\frac{4}{8}\)
1 x 8 = 8
4 x 2 = 8
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{1}{2}\), \(\frac{4}{8}\) are equal ratios.
c. \(\frac{5}{6}\), \(\frac{15}{18}\)
Answer: \(\frac{5}{6}\), \(\frac{15}{18}\) are equal ratios
\(\frac{5}{6}\), \(\frac{15}{18}\)
5 x 18 = 90
6 x 15 = 90
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{5}{6}\), \(\frac{15}{18}\) are equal ratios.
Question 3.
a. \(\frac{5}{8}\), \(\frac{4}{7}\)
Answer: \(\frac{5}{8}\), \(\frac{4}{7}\) are unequal ratios
\(\frac{5}{8}\), \(\frac{4}{7}\)
5 x 7 = 35
4 x 8 = 32
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{5}{8}\), \(\frac{4}{7}\) are unequal ratios.
b. \(\frac{1}{2}\), \(\frac{1}{4}\)
Answer: \(\frac{1}{2}\), \(\frac{1}{4}\) are unequal ratios
\(\frac{1}{2}\), \(\frac{1}{4}\)
1 x 4 = 4
1 x 2 = 2
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{1}{2}\), \(\frac{1}{4}\) are unequal ratios.
c. \(\frac{4}{3}\), \(\frac{16}{12}\)
Answer: \(\frac{4}{3}\), \(\frac{16}{12}\) are equal ratios
\(\frac{4}{3}\), \(\frac{16}{12}\)
4 x 12 = 48
16 x 3 = 48
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{4}{3}\), \(\frac{16}{12}\) are unequal ratios.
Question 4.
a. \(\frac{6}{18}\), \(\frac{2}{6}\)
Answer: \(\frac{6}{18}\), \(\frac{2}{6}\) are equal ratios
\(\frac{6}{18}\), \(\frac{2}{6}\)
6 x 6 = 36
18 x 2 = 36
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{6}{18}\), \(\frac{2}{6}\) are equal ratios.
b. \(\frac{3}{25}\), \(\frac{6}{50}\)
Answer: \(\frac{3}{25}\), \(\frac{6}{50}\) are equal ratios
\(\frac{3}{25}\), \(\frac{6}{50}\)
3 x 50 = 150
25 x 6 =150
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{3}{25}\), \(\frac{6}{50}\) are equal ratios.
c. \(\frac{1}{8}\), \(\frac{2}{10}\)
Answer: \(\frac{1}{8}\), \(\frac{2}{10}\) are unequal ratios
\(\frac{1}{8}\), \(\frac{2}{10}\)
1 x 10 = 10
2 x 8 = 16
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{1}{8}\), \(\frac{2}{10}\) are unequal ratios.
Question 5.
a. \(\frac{1}{4}\), \(\frac{2}{4}\)
Answer: \(\frac{1}{4}\), \(\frac{2}{4}\) are unequal ratios
\(\frac{1}{4}\), \(\frac{2}{4}\)
1 x 4 = 4
2 x 4 = 8
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{1}{4}\), \(\frac{2}{4}\) are unequal ratios.
b. \(\frac{5}{10}\), \(\frac{3}{6}\)
Answer: \(\frac{5}{10}\), \(\frac{3}{6}\) are equal ratios
\(\frac{5}{10}\), \(\frac{3}{6}\)
5 x 6 = 30
10 x 3 = 30
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{5}{10}\), \(\frac{3}{6}\) are equal ratios.
c. \(\frac{4}{24}\), \(\frac{7}{42}\)
Answer: \(\frac{4}{24}\), \(\frac{7}{42}\) are equal ratios
\(\frac{4}{24}\), \(\frac{7}{42}\)
4 x 42 = 168
24 x 7 = 168
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{4}{24}\), \(\frac{7}{42}\) are equal ratios.
Question 6.
a. \(\frac{3}{5}\), \(\frac{5}{3}\)
Answer: \(\frac{3}{5}\), \(\frac{5}{3}\) are unequal ratios
\(\frac{3}{5}\), \(\frac{5}{3}\)
3 x 3 = 9
5 x 5 = 25
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{3}{5}\), \(\frac{5}{3}\) are unequal ratios.
b. \(\frac{7}{8}\), \(\frac{21}{24}\)
Answer: \(\frac{7}{8}\), \(\frac{21}{24}\) are equal ratios
\(\frac{7}{8}\), \(\frac{21}{24}\)
7 x 24 = 168
21 x 8 = 168
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{7}{8}\), \(\frac{21}{24}\) are equal ratios.
c. \(\frac{8}{23}\), \(\frac{9}{46}\)
Answer: \(\frac{8}{23}\), \(\frac{9}{46}\) are unequal ratios
\(\frac{8}{23}\), \(\frac{9}{46}\)
8 x 46 = 368
9 x 23 =207
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{8}{23}\), \(\frac{9}{46}\) are unequal ratios.
Question 7.
a. \(\frac{7}{4}\), \(\frac{28}{16}\)
Answer: \(\frac{7}{4}\), \(\frac{28}{16}\) are equal ratios
\(\frac{7}{4}\), \(\frac{28}{16}\)
7 x 16 =112
28 x 4 = 112
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{7}{4}\), \(\frac{28}{16}\) are equal ratios.
b. \(\frac{3}{9}\), \(\frac{1}{3}\)
Answer: \(\frac{3}{9}\), \(\frac{1}{3}\) are equal ratios
\(\frac{3}{9}\), \(\frac{1}{3}\)
3 x 3 = 9
9 x 1 = 9
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{3}{9}\), \(\frac{1}{3}\) are equal ratios.
c. \(\frac{16}{20}\), \(\frac{9}{10}\)
Answer: \(\frac{16}{20}\), \(\frac{9}{10}\) are unequal ratios
\(\frac{16}{20}\), \(\frac{9}{10}\)
16 x 10 = 160
20 x 9 = 180
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{16}{20}\), \(\frac{9}{10}\) are unequal ratios.
Question 8.
a. \(\frac{8}{100}\), \(\frac{80}{50}\)
Answer: \(\frac{8}{100}\), \(\frac{80}{50}\) are unequal ratios
\(\frac{8}{100}\), \(\frac{80}{50}\)
8 x 50 = 400
80 x 100 = 8000
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{8}{100}\), \(\frac{80}{50}\) are unequal ratios.
b. \(\frac{8}{12}\), \(\frac{10}{14}\)
Answer: \(\frac{8}{12}\), \(\frac{10}{14}\) are unequal ratios
\(\frac{8}{12}\), \(\frac{10}{14}\)
8 x 14 =112
12 x 10 = 120
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{8}{12}\), \(\frac{10}{14}\) are unequal ratios.
c. \(\frac{15}{20}\), \(\frac{3}{4}\)
Answer: \(\frac{15}{20}\), \(\frac{3}{4}\) are equal ratios
\(\frac{15}{20}\), \(\frac{3}{4}\)
15 x 4 = 60
3 x 20 = 60
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{15}{20}\), \(\frac{3}{4}\) are equal ratios.
Question 9.
a. \(\frac{9}{2}\), \(\frac{12}{3}\)
Answer: \(\frac{9}{2}\), \(\frac{12}{3}\) are unequal ratios
\(\frac{9}{2}\), \(\frac{12}{3}\)
9 x 3 = 27
2 x 12 = 24
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{9}{2}\), \(\frac{12}{3}\) are unequal ratios.
b. \(\frac{6}{3}\), \(\frac{8}{4}\)
Answer: \(\frac{6}{3}\), \(\frac{8}{4}\) are equal ratios
\(\frac{6}{3}\), \(\frac{8}{4}\)
6 x 4 = 24
8 x 3 =24
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{6}{3}\), \(\frac{8}{4}\) are equal ratios.
c. \(\frac{1}{3}\), \(\frac{11}{33}\)
Answer: \(\frac{1}{3}\), \(\frac{11}{33}\) are equal ratios
\(\frac{1}{3}\), \(\frac{11}{33}\)
1 x 33 = 33
3 x 11 = 33
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{1}{3}\), \(\frac{11}{33}\) are equal ratios.
Question 10.
a. \(\frac{12}{7}\), \(\frac{36}{21}\)
Answer: \(\frac{12}{7}\), \(\frac{36}{21}\) are equal ratios
\(\frac{12}{7}\), \(\frac{36}{21}\)
12 x 21 = 252
7 x 36 = 252
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{12}{7}\), \(\frac{36}{21}\) are equal ratios.
b. \(\frac{10}{12}\), \(\frac{15}{20}\)
Answer: \(\frac{10}{12}\), \(\frac{15}{20}\) are unequal ratios
\(\frac{10}{12}\), \(\frac{15}{20}\)
10 x 20 = 200
12 x 15 = 180
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{10}{12}\), \(\frac{15}{20}\) are unequal ratios.
c. \(\frac{3}{4}\), \(\frac{9}{16}\)
Answer: \(\frac{3}{4}\), \(\frac{9}{16}\) are unequal ratios
\(\frac{3}{4}\), \(\frac{9}{16}\)
3 x 16 = 48
4 x 9 = 36
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{3}{4}\), \(\frac{9}{16}\) are unequal ratios.
Cross-multiply to check each proportion. Circle the ratios that are true.
Question 1.
a. \(\frac{4}{3}\) = \(\frac{6}{4}\)
Answer: \(\frac{4}{3}\) , \(\frac{6}{4}\) are unequal fractions
\(\frac{4}{3}\) , \(\frac{6}{4}\)
4 x 4 = 16
6 x 3 = 18
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{4}{3}\) , \(\frac{6}{4}\) are unequal ratios.
b. \(\frac{1}{4}\) , \(\frac{3}{12}\)
Answer: \(\frac{1}{4}\) , \(\frac{3}{12}\) are equal fractions
\(\frac{1}{4}\) , \(\frac{3}{12}\)
1 x 12 = 12
3 x 4 = 12
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{1}{4}\) , \(\frac{3}{12}\) are equal ratios.
c. \(\frac{4}{5}\) , \(\frac{16}{20}\)
Answer: \(\frac{4}{5}\) , \(\frac{16}{20}\) are equal fractions
\(\frac{4}{5}\) , \(\frac{16}{20}\)
4 x 20 = 80
5 x 16 = 80
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{4}{5}\) , \(\frac{16}{20}\) are equal ratios.
Question 2.
a. \(\frac{8}{12}\) , \(\frac{2}{3}\)
Answer: \(\frac{8}{12}\) , \(\frac{2}{3}\) are equal fractions
\(\frac{8}{12}\) , \(\frac{2}{3}\)
8 x 3 = 24
12 x 2 = 24
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{8}{12}\) , \(\frac{2}{3}\) are equal ratios.
b. \(\frac{30}{25}\) = \(\frac{6}{5}\)
Answer: \(\frac{30}{25}\) , \(\frac{6}{5}\) are equal fractions
\(\frac{30}{25}\) , \(\frac{6}{5}\)
30 x 5 = 150
25 x 6 = 150
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{30}{25}\) , \(\frac{6}{5}\) are equal ratios.
c. \(\frac{7}{3}\) = \(\frac{5}{2}\)
Answer: \(\frac{7}{3}\) , \(\frac{5}{2}\) are unequal fractions
\(\frac{7}{3}\) , \(\frac{5}{2}\)
7 x 2 = 14
3 x 5 =15
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{7}{3}\), \(\frac{5}{2}\) are unequal ratios.
Question 3.
a. \(\frac{9}{1}\) = \(\frac{18}{3}\)
Answer: \(\frac{9}{1}\), \(\frac{18}{3}\)are unequal fractions
\(\frac{9}{1}\), \(\frac{18}{3}\)
9 x 3 = 27
1 x 18 =18
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{9}{1}\), \(\frac{18}{3}\) are unequal ratios.
b. \(\frac{15}{4}\) = \(\frac{45}{12}\)
Answer: \(\frac{15}{4}\) , \(\frac{45}{12}\) are equal fractions
\(\frac{15}{4}\), \(\frac{45}{12}\)
15 x 12 = 180
4 x 45 = 180
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{15}{4}\), \(\frac{45}{12}\) are equal ratios.
c. \(\frac{2}{5}\) = \(\frac{4}{12}\)
Answer: \(\frac{2}{5}\), \(\frac{4}{12}\) are unequal fractions
\(\frac{2}{5}\), \(\frac{4}{12}\)
2 x 12 = 24
5 x 4 = 20
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{2}{5}\), \(\frac{4}{12}\) are unequal ratios.
Question 4.
a. \(\frac{7}{4}\) = \(\frac{21}{12}\)
Answer: \(\frac{7}{4}\), \(\frac{21}{12}\) are equal fractions
\(\frac{7}{4}\), \(\frac{21}{12}\)
7 x 12 = 84
21 x 4 = 84
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{7}{4}\), \(\frac{21}{12}\) are equal ratios.
b. \(\frac{9}{2}\) = \(\frac{18}{6}\)
Answer: \(\frac{9}{2}\), \(\frac{18}{6}\) are unequal fractions
\(\frac{9}{2}\), \(\frac{18}{6}\)
9 x 6 = 54
2 x 18 = 36
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{9}{2}\), \(\frac{18}{6}\) are unequal ratios.
c. \(\frac{5}{6}\) = \(\frac{15}{18}\)
Answer: \(\frac{5}{6}\) , \(\frac{15}{18}\) are equal ratios
\(\frac{5}{6}\) , \(\frac{15}{18}\)
5 x 18 = 90
6 x 15 = 90
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{5}{6}\) , \(\frac{15}{18}\) are equal ratios.
Question 5.
a. \(\frac{5}{9}\) = \(\frac{10}{19}\)
Answer: \(\frac{5}{9}\) , \(\frac{10}{19}\) are unequal fractions
\(\frac{5}{9}\), \(\frac{10}{19}\)
5 x 19 = 95
10 x 9 = 90
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{5}{9}\), \(\frac{10}{19}\)are unequal ratios.
b. \(\frac{4}{3}\) = \(\frac{16}{12}\)
Answer: \(\frac{4}{3}\), \(\frac{16}{12}\) are equal fractions
\(\frac{4}{3}\), \(\frac{16}{12}\)
4 x 12 = 48
3 x 16 = 48
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{4}{3}\), \(\frac{16}{12}\) are equal ratios.
c. \(\frac{7}{4}\) = \(\frac{14}{10}\)
Answer: \(\frac{7}{4}\) , \(\frac{14}{10}\) are unequal fractions
\(\frac{7}{4}\), \(\frac{14}{10}\)
7 x 10 = 70
4 x 14 = 56
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{7}{4}\), \(\frac{14}{10}\)are unequal ratios.
Question 6.
a. \(\frac{12}{8}\) = \(\frac{18}{12}\)
Answer: \(\frac{12}{8}\), \(\frac{18}{12}\) are equal fractions
\(\frac{12}{8}\) , \(\frac{18}{12}\)
12 x 12 = 144
8 x 18 = 144
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{12}{8}\) , \(\frac{18}{12}\) are equal ratios.
b. \(\frac{14}{7}\) = \(\frac{6}{3}\)
Answer: \(\frac{14}{7}\), \(\frac{6}{3}\) are equal fractions
\(\frac{14}{7}\) , \(\frac{6}{3}\)
14 x 3 = 42
7 x 6 = 42
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{14}{7}\) , \(\frac{6}{3}\) are equal ratios.
c. \(\frac{1}{5}\) = \(\frac{3}{16}\)
Answer: \(\frac{1}{5}\) , \(\frac{3}{16}\) are unequal fractions
\(\frac{1}{5}\), \(\frac{3}{16}\)
1 x 16 = 16
5 x 3 = 15
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{1}{5}\), \(\frac{3}{16}\) are unequal ratios.
Question 7.
a. \(\frac{2}{1}\) = \(\frac{6}{2}\)
Answer: \(\frac{2}{1}\) , \(\frac{6}{2}\) are unequal fractions
\(\frac{2}{1}\), \(\frac{6}{2}\)
2 x 2 = 4
1 x 6 = 6
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{2}{1}\), \(\frac{6}{2}\) are unequal ratios.
b. \(\frac{8}{6}\) = \(\frac{12}{8}\)
Answer: \(\frac{8}{6}\) , \(\frac{12}{8}\) are unequal fractions
\(\frac{8}{6}\), \(\frac{12}{8}\)
8 x 8 = 64
6 x 12 = 72
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{8}{6}\), \(\frac{12}{8}\) are unequal ratios.
c. \(\frac{5}{4}\) = \(\frac{10}{8}\)
Answer: \(\frac{5}{4}\) , \(\frac{10}{8}\) are equal fractions
\(\frac{5}{4}\) , \(\frac{10}{8}\)
5 x 8 = 40
4 x 10 = 40
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{5}{4}\) , \(\frac{10}{8}\) are equal ratios.
Question 8.
a. \(\frac{2}{5}\) = \(\frac{6}{15}\)
Answer: \(\frac{2}{5}\), \(\frac{6}{15}\) are equal fractions
\(\frac{2}{5}\) , \(\frac{6}{15}\)
2 x 15 = 30
6 x 5 = 30
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{2}{5}\) , \(\frac{6}{15}\) are equal ratios.
b. \(\frac{14}{6}\) = \(\frac{21}{8}\)
Answer: \(\frac{14}{6}\), \(\frac{21}{8}\) are unequal fractions
\(\frac{14}{6}\), \(\frac{21}{8}\)
14 x 8 = 112
6 x 21 = 126
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{14}{6}\), \(\frac{21}{8}\) are unequal ratios.
c. \(\frac{4}{5}\) = \(\frac{10}{16}\)
Answer: \(\frac{4}{5}\), \(\frac{10}{16}\) are unequal fractions
\(\frac{4}{5}\) , \(\frac{10}{16}\)
4 x 16 = 64
5 x 10 = 50
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{4}{5}\) , \(\frac{10}{16}\) are unequal ratios.
Question 9.
a. \(\frac{3}{5}\) = \(\frac{9}{20}\)
Answer: \(\frac{3}{5}\),\(\frac{9}{20}\) are unequal fractions
\(\frac{3}{5}\), \(\frac{9}{20}\)
3 x 20 = 60
5 x 9 = 45
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{3}{5}\), \(\frac{9}{20}\) are unequal ratios.
b. \(\frac{1}{3}\) = \(\frac{4}{12}\)
Answer: \(\frac{1}{3}\), \(\frac{4}{12}\) are equal fractions
\(\frac{1}{3}\) , \(\frac{4}{12}\)
1 x 12 = 12
4 x 3 = 12
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{1}{3}\) , \(\frac{4}{12}\) are equal ratios.
c. \(\frac{9}{6}\) = \(\frac{12}{8}\)
Answer: \(\frac{9}{6}\), \(\frac{12}{8}\) are equal fractions
\(\frac{9}{6}\), \(\frac{12}{8}\)
9 x 8 = 72
6 x 12 = 72
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{9}{6}\), \(\frac{12}{8}\) are equal ratios.
Question 10.
a. \(\frac{7}{5}\) = \(\frac{28}{20}\)
Answer: \(\frac{7}{5}\), \(\frac{28}{20}\) are equal fractions
\(\frac{7}{5}\), \(\frac{28}{20}\)
7 x 20 = 140
5 x 28 = 140
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{7}{5}\), \(\frac{28}{20}\) are equal ratios.
b. \(\frac{5}{4}\) = \(\frac{25}{16}\)
Answer: \(\frac{5}{4}\), \(\frac{25}{16}\) are unequal fractions
\(\frac{5}{4}\), \(\frac{25}{16}\)
5 x 16 =80
25 x 4 = 100
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{5}{4}\), \(\frac{25}{16}\) are unequal ratios.
c. \(\frac{10}{13}\) = \(\frac{30}{26}\)
Answer: \(\frac{10}{13}\) , \(\frac{30}{26}\) are unequal fractions
\(\frac{10}{13}\), \(\frac{30}{26}\)
10 x 26 = 260
13 x 30 = 390
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{10}{13}\), \(\frac{30}{26}\) are unequal ratios.
Question 11.
a. \(\frac{4}{5}\) = \(\frac{20}{22}\)
Answer: \(\frac{4}{5}\) , \(\frac{20}{22}\) are unequal fractions
\(\frac{4}{5}\) , \(\frac{20}{22}\)
4 x 22 = 88
5 x 20 = 100
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{4}{5}\) , \(\frac{20}{22}\) are unequal ratios.
b. \(\frac{1}{5}\) = \(\frac{3}{18}\)
Answer: \(\frac{1}{5}\) , \(\frac{3}{18}\) are unequal fractions
\(\frac{1}{5}\), \(\frac{3}{18}\)
1 x 18 = 18
5 x 3 = 15
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{1}{5}\), \(\frac{3}{18}\) are unequal ratios.
c. \(\frac{6}{7}\) = \(\frac{78}{91}\)
Answer: \(\frac{6}{7}\), \(\frac{78}{91}\) are equal ratios
\(\frac{6}{7}\) , \(\frac{78}{91}\)
6 x 91 = 546
7 x 78 = 546
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{6}{7}\) , \(\frac{78}{91}\) are equal ratios.
Question 12.
a. \(\frac{2}{9}\) = \(\frac{30}{135}\)
Answer: \(\frac{2}{9}\), \(\frac{30}{135}\)
\(\frac{2}{9}\) , \(\frac{30}{135}\)
2 x 135 = 270
9 x 30 = 270
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{2}{9}\) , \(\frac{30}{135}\) are equal ratios.
b. \(\frac{8}{3}\) = \(\frac{96}{36}\)
Answer: \(\frac{8}{3}\) , \(\frac{96}{36}\) are equal ratios
\(\frac{8}{3}\), \(\frac{96}{36}\)
8 x 36 = 288
9 x 96 = 288
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{8}{3}\), \(\frac{96}{36}\) are equal ratios.
c. \(\frac{5}{2}\) = \(\frac{75}{20}\)
Answer: \(\frac{5}{2}\), \(\frac{75}{20}\) are unequal fractions
\(\frac{5}{2}\), \(\frac{75}{20}\)
5 x 20 = 100
2 x 75 = 150
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is not same after cross multiplication.
Therefore, \(\frac{5}{2}\), \(\frac{75}{20}\) are unequal ratios.