This handy Spectrum Math Grade 7 Answer Key Chapter 4 Pretest provides detailed answers for the workbook questions
Spectrum Math Grade 7 Chapter 4 Pretest Answers Key
Ratios and Proportional Relationships
Solve each proportion.
Question 1.
a.
\(\frac{8}{15}\) = \(\frac{24}{n}\)
Answer: n = 45
\(\frac{8}{15}\) = \(\frac{24}{n}\)
In order to solve the above proportion and get the value of n, perform cross multiplication
As product of means = product of extremes
8 × n = 15 × 24
8n = 360
n = \(\frac{360}{8}\)
Therefore, n = 45
b.
\(\frac{3}{6}\) = \(\frac{n}{2}\)
Answer: n = 1
\(\frac{3}{6}\) = \(\frac{n}{2}\)
In order to solve the above proportion and get the value of n, perform cross multiplication
As product of means = product of extremes
6 × n = 3 × 2
6n = 6
n = \(\frac{6}{6}\)
Therefore, n = 1
c.
\(\frac{7}{n}\) = \(\frac{14}{16}\)
Answer: n = 8
\(\frac{7}{n}\) = \(\frac{14}{16}\)
In order to solve the above proportion and get the value of n, perform cross multiplication
As product of means = product of extremes
14 × n = 7 × 16
14n = 112
n = \(\frac{112}{14}\)
Therefore, n = 8
Question 2.
a.
\(\frac{8}{n}\) = \(\frac{1}{3}\)
Answer: n = 24
\(\frac{8}{n}\) = \(\frac{1}{3}\)
In order to solve the above proportion and get the value of n, perform cross multiplication
As product of means = product of extremes
1 × n = 8 × 3
Therefore, n = 24
b.
\(\frac{n}{10}\) = \(\frac{4}{8}\)
Answer: n = 5
\(\frac{n}{10}\) = \(\frac{4}{8}\)
In order to solve the above proportion and get the value of n, perform cross multiplication
As product of means = product of extremes
8 × n = 4 × 10
8n = 40
n = \(\frac{40}{8}\)
Therefore, n = 5
c.
\(\frac{6}{n}\) = \(\frac{16}{24}\)
Answer: n = 9
\(\frac{6}{n}\) = \(\frac{16}{24}\)
In order to solve the above proportion and get the value of n, perform cross multiplication
As product of means = product of extremes
16 × n = 6 × 24
16n = 144
n = \(\frac{144}{16}\)
Therefore, n = 9
Circle the ratios that are equal. Show your work.
Question 3.
a. \(\frac{3}{9}\), \(\frac{1}{3}\)
Answer:
\(\frac{3}{9}\), \(\frac{1}{3}\)
3 × 3 = 9
1 × 9 = 9
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{3}{9}\), \(\frac{1}{3}\) are equal ratios.
b. \(\frac{6}{18}\), \(\frac{2}{6}\)
Answer:
\(\frac{6}{18}\), \(\frac{2}{6}\)
6 × 6 = 36
18 × 2 = 36
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{6}{18}\), \(\frac{2}{6}\) are equal ratios.
c. \(\frac{1}{2}\), \(\frac{1}{4}\)
Answer:
\(\frac{1}{2}\), \(\frac{1}{4}\)
1 × 4 = 4
1 × 2 = 2
A ratio is a comparison of two numbers. A proportion expresses the equality of two ratios.
In order to determine whether the two ratios are equal or not, cross multiply both the ratios. If the results after cross multiplication is same on both sides, then they are said to be equal. Otherwise they are said to be unequal ratios.
In the above given ratios the result is same after cross multiplication.
Therefore, \(\frac{1}{2}\), \(\frac{1}{4}\) are not equal ratios.
Find the constant of proportionality for each set of values.
Question 4.
a.
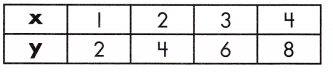
k = _____
Answer: k = 2
Step 1: Set up an equation in which the constant (k) is equal to y ÷ x.
Step 2: Check the equation across multiple points to verify the constant.
Step 3: 2 ÷ 1 = 2 ,
4 ÷ 2 = 2 ,
6 ÷ 3 = 2,
8 ÷ 4 = 2
Therefore, k = 2
b.
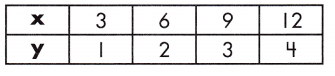
k = _____
Answer: k = 0.333
Step 1: Set up an equation in which the constant (k) is equal to y ÷ x.
Step 2: Check the equation across multiple points to verify the constant.
Step 3: 1 ÷ 3 = 0.333 ,
2 ÷ 6 = 0.333 ,
3 ÷ 9 = 0.333,
4 ÷ 12 = 0.333
Therefore, k = 0.333
Find the constant of proportionality.
Question 5.
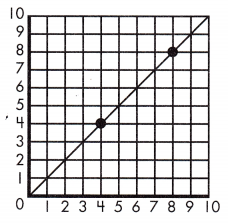
k = _____
Answer: k = 1
When proportional relationships are graphed, the points the line runs through can be used to find the constant of proportionality.
This line runs through points (4,4) and (8,8).
First, find the proportion of this relationship by choosing one point and inserting its coordinates into the proportion equation.
k = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) k = \(\frac{8-4}{8-4}\) = \(\frac{4}{4}\) = 1
The constant of proportionality for this line is 1.
Therefore, k = 1
Solve each problem.
Question 6.
Three baskets of oranges weigh 120 pounds. How many pounds are in 4 baskets?
There are ____________________ pounds in 4 baskets.
Answer: There are 160 pounds in 4 baskets.
Three baskets of oranges weigh 120 pounds.
We need to find number of pounds in 4 baskets.
Let p represent number of pounds
Proportional relationships can be used to solve ratio and percent problems.
Now, write a proportion using the above information
\(\frac{3}{120}\) = \(\frac{4}{p}\)
By cross multiplication,
3 × p = 4 × 120
3p = 480
n = \(\frac{480}{3}\)
Therefore, n = 160
So, There are 160 pounds in 4 baskets.
Question 7.
There are 60 pencils ¡n 4 pencil boxes. How many pencils are in 7 boxes?
There are ___________________ pencils in 7 boxes.
Answer: There are 105 pencils in 7 boxes.
There are 60 pencils ¡n 4 pencil boxes.
We need to find number of pencils in 7 boxes
Let p represent number of pencils
Proportional relationships can be used to solve ratio and percent problems.
Now, write a proportion using the above information
\(\frac{4}{60}\) = \(\frac{7}{p}\)
By cross multiplication,
4 × p = 7 × 60
4p = 420
n = \(\frac{420}{4}\)
Therefore, n = 105
So, There are 105 pencils in 7 boxes.
Question 8.
The supply store sells 4 pencils for every 5 pens. The store sold 28 pencils yesterday. How many pens did
it sell?
The store sold _____________________ pens.
Answer: The store sold 35 pens.
The supply store sells 4 pencils for every 5 pens.
We need to find the number of pens sold for 28 pencils
Let p represent number of pens
Proportional relationships can be used to solve ratio and percent problems.
Now, write a proportion using the above information
\(\frac{4}{5}\) = \(\frac{28}{p}\)
By cross multiplication,
4 × p = 5 × 28
4p = 140
n = \(\frac{140}{4}\)
Therefore, n = 35
So, The store sold 35 pens.
Question 9.
A restaurant charges an automatic 20% tip for groups of 6 or more. A group of 8 people had a bill of $187.
How much was their tip?
Their tip was ____.
Answer: Their tip was $31.167
A restaurant charges an automatic 20% tip for groups of 6 or more.
A group of 8 people had a bill of $187
Let x be the bill before adding tip
Equation: x + 20% × x = $187
x + \(\frac{20}{100}\) × x = $187
x + 0.2x = $187
x ( 1 + 0.2) = $187
1.2x = $187
x = \(\frac{$187}{1.2}\)
x = $155.833
So, the bill before adding tip = $155.833
Therefore tip = $187 – $155.833 = $31.167
So, Their tip was $31.167
Question 10.
A mail order company charges 4% for shipping and handling on all orders. If the total for on order is $54.34, how much was the order total before shipping and handling?
Let r stand for the order total.
Equation: _______________________
The order before shipping and handling is ___________________________ .
Answer: Equation: x + 4% × x = $54.34
The order before shipping and handling is $52.25
A mail order company charges 4% for shipping and handling on all orders.
The total for on order is $54.34
let x be the order total before shipping and handling
Equation: x + 4% × x = $54.34
x + \(\frac{4}{100}\) × x = $54.34
x + 0.04x = $54.34
x ( 1 + 0.04) = $54.34
1.04x = $54.34
x = \(\frac{$54.34}{1.04}\)
Therefore, x = $52.25
So, The order before shipping and handling is $52.25
Question 11.
Elizabeth can run 5 miles in 24\(\frac{1}{2}\) minutes. Dez can run 8 miles in 32\(\frac{1}{3}\) minutes. Who can run faster?
Let e represent Elizabeth’s speed and d represent Dez’s speed.
Equivalent Ratio 1: ______________________
Equivalent Ratio 2: ____________________
_________________ can run faster.
Answer: Equivalent Ratio 1: \(\frac{5}{24 \frac{1}{2}}\) = \(\frac{d}{t}\) e
Equivalent Ratio 2: \(\frac{8}{32 \frac{1}{3}}\) = \(\frac{d}{t}\) d
Dez can run faster.
Elizabeth can run 5 miles in 24\(\frac{1}{2}\) minutes.
Dez can run 8 miles in 32\(\frac{1}{3}\) minutes.
Let e represent Elizabeth’s speed and d represent Dez’s speed.
Equivalent Ratio 1: \(\frac{5}{24 \frac{1}{2}}\) = \(\frac{d}{t}\) e
\(\frac{5}{ \frac{49}{2}}\) = \(\frac{d}{t}\) e
= \(\frac{10}{49}\) = 0.20408
Equivalent Ratio 2: \(\frac{8}{32 \frac{1}{3}}\) = \(\frac{d}{t}\) d
\(\frac{8}{\frac{97}{3}}\) = \(\frac{d}{t}\) d
= \(\frac{24}{97}\) = 0.247422
Therefore, by comparing the above equivalent ratios, Dez can run faster.