Students who are searching to get Math Relation problems can check the Worksheet on Math Relation. Our Math Relation Worksheets available improves your preparation level and are very helpful in your practice. It included various models of questions on Math Relations. Therefore, practice all the given examples and check out the answers to cross-check your method of solving. Practice different questions related to Ordered Pair, Cartesian Product of Two Sets, Relation, Domain, and Range of a Relation in Math Relation Worksheet.
See More: Sets
Relations and Functions Questions and Answers
1. Find the values of x and y, if (x + 4, y – 8) = (8, 1).
Solution:
Given that (x + 4, y – 8) = (8, 1)
Compare the elements of the given ordered pairs.
Firstly, compare the first components of the given ordered pairs.
x + 4 = 8
x = 8 – 4 = 4
So, x = 4.
Now, compare the second components of the given ordered pairs.
y – 8 = 1
y = 8 + 1 = 9
So, y = 9.
Therefore, the value of x = 4 and y = 9.
2. If (x/5 + 3, y – 5/7) = (4, 5/14), find the values of x and y.
Solution:
Given that (x/5 + 3, y – 5/7) = (4, 5/14)
Compare the elements of the given ordered pairs.
Firstly, compare the first components of the given ordered pairs.
x/5 + 3 = 4
x/5 = 4-3
Therefore, x/5 = 1
x = 1 * 5 = 5
So, x = 5.
Now, compare the second components of the given ordered pairs.
y – 5/7 = 5/14
y = 5/14 + 5/7 = 15/14
So, y = 15/14.
Therefore, the value of x = 5 and y = 15/14.
3. If X = {m, n, o} and Y = {u, v}, find X × Y and Y × X. Are the two products equal?
Solution:
Given that X = {m, n, o} and Y = {u, v},
Let’s find the X × Y
X × Y = {(m, u); (m, v); (n, u); (n, v); (o, u); (o, v)}
Now, find Y × X.
Y × X = {(u, m); (u, n); (u, o); (v, m); (v, n); (v, o)}
Compare the elements of the given ordered pairs X and Y.
X × Y not equal to Y × X
Therefore, it is clearly stated that the two products are not equal.
4. If P × Q = {(x, 7); (x, 9); (y, 7); (y, 9); (z, 7); (z, 9)}, find P and Q.
Solution:
Given that P × Q = {(x, 7); (x, 9); (y, 7); (y, 9); (z, 7); (z, 9)},
We know that P is a set of all first entries in ordered pairs in P × Q.
Q is a set of all second entries in ordered pairs in P × Q.
Therefore, P = {x, y, z}
Q = {7, 9}
Therefore, the final answer is P = {x, y, z} and Q = {7, 9}
5. If M and N are two sets, and M × N consists of 6 elements: If three elements of M × N are (8, 4) (7, 3) (6, 3). Find M × N.
Solution:
Given that M and N are two sets, and M × N consists of 6 elements: If three elements of M × N are (8, 4) (7, 3) (6, 3).
We know that M is a set of all first entries in ordered pairs in M × N.
N is a set of all second entries in ordered pairs in M × N.
Therefore, M = {8, 7, 6}, and N = {4, 3}
Now, M × N = {(8, 4); (8, 3); (7, 4); (7, 3); (6, 4); (6, 3)}
Thus, M × N contains six ordered pairs.
6. If A × B = {(m, 3); (m, 7); (m, 4); (n, 3); (n, 7); (n, 4)}, find B × A.
Solution:
Given that A × B = {(m, 3); (m, 7); (m, 4); (n, 3); (n, 7); (n, 4)},
We know that A is a set of all first entries in ordered pairs in A × B.
B is a set of all second entries in ordered pairs in A × B.
Therefore, A = {m, n}, and B = {3, 7, 4}
Now, B × A = {(3, m); (3, n); (7, m); (7, n); (4, m); (4, n)}
Therefore, the final answer is B × A = {(3, m); (3, n); (7, m); (7, n); (4, m); (4, n)}
7. If P = { 2, 1, 9} and Q = {4, 5}, then
Find: (i) P × Q (ii) Q × P (iii) P × P (iv) (Q × Q)
Solution:
Given that P = { 2, 1, 9} and Q = {4, 5}
(i) P × Q = {(2, 4); (2, 5); (1, 4); (1, 5); (9, 4); (9, 5)}
(ii) Q × P = {(4, 2); (4, 1); (4, 9); (5, 2); (5, 1); (5, 9)}
(iii) P × P = {(2, 2); (2, 1); (2, 9); (1, 2); (1, 1); (1, 9); (9, 2); (9, 1); (9, 9)}
(iv) (Q × Q) = {(4, 4); (4, 5); (5, 4); (5, 5)}
8. If P = {3, 5, 7} and Q = {2, 3, 6}, state which of the following is a relation from P to Q.
(a) R₁ = {(3, 5); (6, 7); (7, 2)} (b) R₂ = {(3, 3); (7, 6)}
(c) R₃ = {(3, 2); (5, 6); (6, 7)} (d) R₄ = {(7, 2); (7, 6); (5, 3); (3, 3), (5, 2), (5, 7)}
Solution:
Given that P = {3, 5, 7} and Q = {2, 3, 6}
Note: Every element of set P is associated with a unique element of set Q. No element of P must have more than one image.
(a) f(1) = 3 and f(1) = 5 are not possible. so, this relation is not mapping from P to Q.
(b) R₂ = {(3, 3); (7, 6)}. Every element of set P is associated with a unique element of set Q. hence, it is relation from P to Q.
(c) R₃ = {(3, 2); (5, 6); (6, 7)} it’s not relation from P to Q.
(d) R₄ = {(7, 2); (7, 6); (5, 3); (3, 3), (5, 2), (5, 7)} Every element of set P is associated with a unique element of set Q. hence, it is relation from P to Q.
Therefore, the final answer is (b) R₂ = {(3, 3); (7, 6)} and (d) R₄ = {(7, 2); (7, 6); (5, 3); (3, 3), (5, 2), (5, 7)}
9. Write the domain and range of the following relations.
(a) R₁ = {(5, 4); (7, 9); (5, 9); (1, 8); (8, 6); (1, 9)}
(b) R₂ = {(p, 3); (q, 4); (r, 3); (p, 4); (s, 5); (q, 5)}
Solution:
Given that (a) R₁ = {(5, 4); (7, 9); (5, 9); (1, 8); (8, 6); (1, 9)}
(b) R₂ = {(p, 3); (q, 4); (r, 3); (p, 4); (s, 5); (q, 5)}
(a) R₁ = {(5, 4); (7, 9); (5, 9); (1, 8); (8, 6); (1, 9)}
From the given information, the Domain = {1, 5, 7, 8} and Range = {4, 6, 8, 9}
(b) R₂ = {(p, 3); (q, 4); (r, 3); (p, 4); (s, 5); (q, 5)}
From the given information, the Domain = {p, q, r, s} and Range = {3, 4, 5}
10. Let P = {3, 4, 5, 6, 7, 8}. Define a relation R from A to A by R = {(x, y) : y = x + 1}.
- Depict this relation using an arrow diagram.
- Write down the domain and range of R.
Solution:
Given that P = {3, 4, 5, 6, 7, 8}. Define a relation R from A to A by R = {(x, y) : y = x + 1}.
If x = 3, y = x + 1 = 3 + 1 = 4.
x = 4, y = x + 1 = 4 + 1 = 5.
x = 5, y = x + 1 = 5 + 1 = 6.
x = 6, y = x + 1 = 6 + 1 = 7.
x = 7, y = x + 1 = 7 + 1 = 8.
x = 8, y = x + 1 = 8 + 1 = 9.
R = {(3, 4); (4, 5); (5, 6); (6, 7); (7, 8)} where P = {3, 4, 5, 6, 7, 8}.
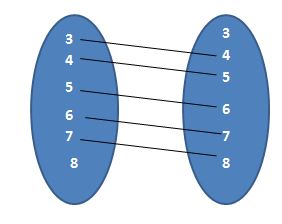
Domain = Set of all first elements in a relation = {3, 4, 5, 6, 7}
Range = Set of all second elements in a relation = {4, 5, 6, 7, 8}
11. Adjoining figure shows a relationship between the set P and Q. Write this relation in the roster form. What are its domain and range?
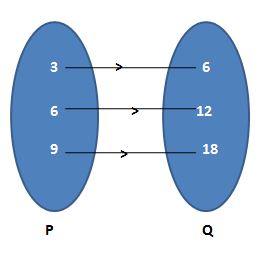
Solution:
The relation mentioned in the figure shows, P a domain and Q as a range.
Let the relation be R.
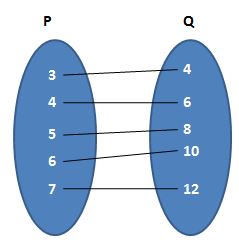
In roster form R = {(3, 6); (6, 12); (9, 18)}
Domain = Set of all first elements in a relation = {3, 6, 9}
Range = Set of all second elements in a relation = {6, 12, 18}
12. In the given ordered pairs (2, 4); (4, 16); (5, 7); (1, 3); (6, 36); (2, 9); (1, 1), find the following relationship:
(a) Is a factor of ….
(b) Is a square root of …..
Also, find the domain and range in each case.
Solution:
Given that the ordered pairs (2, 4); (4, 16); (5, 7); (1, 3); (6, 36); (2, 9); (1, 1).
(a) Is a factor of ….
Let’s find out the factor of …. from the given order pars.
(2, 4); (4, 16); (1, 3); (6, 36); (1, 1)
Domain = Set of all first elements in a relation = {1, 2, 4, 6}
Range = Set of all second elements in a relation = {1, 3, 4, 16, 36}
(b) Is a square root of …..
Let’s find out the square root of …. from the given order pars.
(2, 4); (4, 16); (6, 36).
Domain = Set of all first elements in a relation = {2, 4, 6}
Range = Set of all second elements in a relation = {4, 16, 36}
13. Draw the arrow diagrams to represent the following relations.
(a) R₁ = {(2, 2); (2, 7); (2, 8); (6, 9); (7, 4)}
(b) R₂ = {(5, 11); (5, 14); (5, 17); (6, 14); (7, 17)}
(c) R₃ = {(3, 4); (4, 6); (5, 8); (6, 10); (7, 12)}
(d) R₄ = {(a, x); (a, y); (b, p); (b, z); (c, y)}
Solution:
(a) Given that R₁ = {(2, 2); (2, 7); (2, 8); (6, 9); (7, 4)}
Let the two sets are P and Q.
The required diagram is
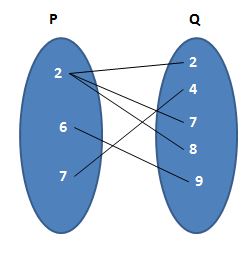
(b) Given that R₂ = {(5, 11); (5, 14); (5, 17); (6, 14); (7, 17)}
Let the two sets are P and Q.
The required diagram is
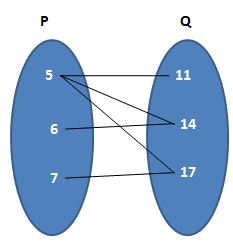
(c) Given that R₃ = {(3, 4); (4, 6); (5, 8); (6, 10); (7, 12)}
Let the two sets are P and Q.
The required diagram is
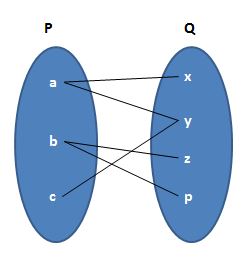
(d) Given that R₄ = {(a, x); (a, y); (b, p); (b, z); (c, y)}
Let the two sets are P and Q.
The required diagram is
14. Represent the following relation in the roster form.
(a) 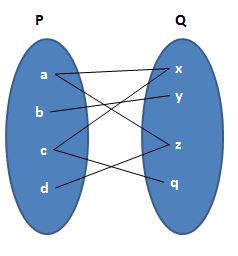
(b) 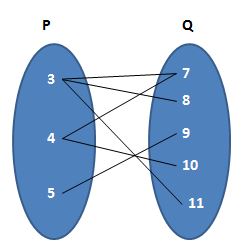
(c) 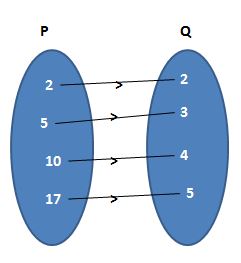
(d) 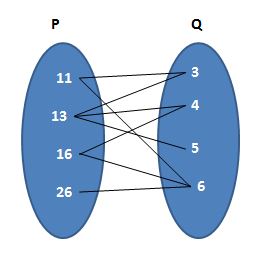
Solution:
(a) R = {(a, x) (a, z) (b, y) (c, x) (c, q) (d, z)}
(b) R = {(3, 7) (3, 9) (4, 7) (4, 10) (5, 9) (3, 11)}
(c) R = {(2, 2) (5, 3) (10, 4) (17, 5)}
(d) R = {(11, 3) (11, 6) (13, 3) (13, 4) (13, 5) (16, 4) (16, 6) (26, 6)}
