If you are ever stuck up during your Homework/ Assignments regarding Algebra Concepts take the help of Big Ideas Math Book Algebra 1 Chapter 4 Writing Linear Functions Answers available. Solve the Big Ideas Math Algebra 1 Answers Chapter 4 Writing Linear Functions Textbook Questions provided with Solutions given by subject experts. Improve your knowledge by practicing from Big Ideas Math Algebra 1 Answers and clear your exams with higher marks. You can download the Writing Linear Functions BIM Algebra 1 Solution Key free of cost and ace up your preparation.
Big Ideas Math Book Algebra 1 Answer Key Chapter 4 Writing Linear Functions
Learn embedded mathematical practices and become proficient in the concepts of Big Ideas Math Algebra 1 Answers Chapter 4 Writing Linear Functions by using the links provided below. In order to access the underlying concepts, all you have to do is simply tap on the respective concepts and prepare accordingly. The Big Ideas Math Algebra 1 Answers Chapter 4 Writing Linear Functions cover the Questions belonging to Exercises, Practice Tests, Cumulative Assessments, Review Tests, Chapter Tests, etc. You can make use of the Reasoning and Proofs Big Ideas Math Algebra 1 Answer Key whenever needed.
- Writing Linear Functions Maintaining Mathematical Proficiency – Page 173
- Writing Linear Functions Mathematical Practices – Page 174
- Lesson 4.1 Writing Equations in Slope-Intercept Form – Page(175-180)
- Writing Equations in Slope-Intercept Form 4.1 Exercises – Page(179-180)
- Lesson 4.2 Writing Equations in Point-Slope Form – Page(181-186)
- Writing Equations in Point-Slope Form 4.2 Exercises -Page(185-186)
- Lesson 4.3 Writing Equations of Parallel and Perpendicular Lines -Page(187-192)
- Writing Equations of Parallel and Perpendicular Lines 4.3 Exercises – Page(191-192)
- Writing Linear Functions Study Skills: Getting Actively Involved in Class – Page 193
- Writing Linear Functions 4.1 – 4.3 – Page 194
- Lesson 4.4 Scatter Plots and Lines of Fit – Page – Page(195-200)
- Scatter Plots and Lines of Fit 4.4 Exercises – Page(199-200)
- Lesson 4.5 Analyzing Lines of Fit – Page(201-208)
- Analyzing Lines of Fit 4.5 Exercises – Page(206-208)
- Lesson 4.6 Arithmetic Sequences – Page(209-216)
- Arithmetic Sequences 4.6 Exercises – Page(214-216)
- Lesson 4.7 Piecewise Functions -Page(217-224)
- Piecewise Functions 4.7 Exercises – Page(222-224)
- Writing Linear Functions Performance Task: Any Beginning – Page 225
- Writing Linear Functions Chapter Review – Page(226-228)
- Writing Linear Functions Chapter Test – Page 229
- Writing Linear Functions Cumulative Assessment – Page(230-231)
Writing Linear Functions Maintaining Mathematical Proficiency
Use the graph to answer the question.
Question 1.
What ordered pair corresponds to point G?
Answer:
The coordinates of point G are (-5, -2).
So, the x coordinate is -5, y coordinate is -2.
The ordered pair (-5, -2) corresponds to point G.
Question 2.
What ordered pair corresponds to point D?
Answer:
The coordinates of point D are (2, 0).
So, the x coordinate is 2, y coordinate is 0.
The ordered pair (2, 0) corresponds to point D.
question 3.
Which point is located in Quadrant I?
Answer:
The coordinates of point C are (3, 5).
So, the x coordinate is 3, y coordinate is 5.
Both coordinates are positive.
So, point C is located in quadrant I.
Question 4.
Which point is located in Quadrant IV?
Answer:
The coordinates of point E are (3, -3).
So, the x coordinate is 3, y coordinate is -3.
x-coordinate is positive and y coordinate is negative.
So point E is located in quadrant IV.
Solve the equation for y.
Question 5.
x – y = 5
Answer:
x – y = 5
x – y – x = 5 – x
-y = 5 – x
-1(-y) = -1(5 – x)
y = x – 5
Question 6.
6x + 3y = -1
Answer:
Given
6x + 3y = -1
3y = -1 – 6x
y = \(\frac { -1 – 6x }{ 3 } \)
Question 7.
0 = 2y – 8x + 10
Answer:
Given
0 = 2y – 8x + 10
8x = 2y + 10
8x – 10 = 2y
y = 4x – 5
Question 8.
-x + 4y – 28 = 0
Answer:
Given,
-x + 4y – 28 = 0
4y – 28 = x
4y = x + 28
y = \(\frac { x + 28 }{ 4 } \)
Question 9.
2y + 1 – x = 7x
Answer:
Given,
2y + 1 – x = 7x
2y + 1 = 7x + x
2y + 1 = 8x
2y = 8x – 1
y = \(\frac { 8x – 1 }{ 2 } \)
Question 10.
y – 4 = 3x + 5y
Answer:
Given,
y – 4 = 3x + 5y
-4 = 3x + 5y – y
-4 = 3x + 4y
4y = -4 – 3x
y = \(\frac { -4 – 3x }{ 4 } \)
Question 11.
ABSTRACT REASONING
Both coordinates of the point (x, y) are multiplied by a negative number. How does this change the location of the point? Be sure to consider points originally located in all four quadrants.
Answer:
If both coordinates of the point in Quadrant I are multiplied by a negative number, then the point is shifted to Quadrant III and vice versa.
If both coordinates of the point in Quadrant II are multiplied by a negative number, then the point is shifted to quadrant IV and vice versa.
Writing Linear Functions Mathematical Practices
Monitoring Progress
Question 1.
You work 37\(\frac{1}{2}\) hours and earn $352.50. What is your hourly wage?
Answer:
Given,
The wage for 37.5 hours is 352.50
1 hour wage = \(\frac { 352.50 }{ 37.5 } \) = 9.4
$9.4 is your hourly wage.
Question 2.
You drive 1244.5 miles and use 47.5 gallons of gasoline. What is your car’s gas mileage (in miles per gallon)?
Answer:
You drive 1244.5 miles and use 47.5 gallons of gasoline.
Car gas milage = \(\frac { 1244.5 }{ 47.5 } \) = 26.2
My car gas mileage is 26.2 miles per gallon.
Question 3.
You drive 236 miles in 4.6 hours. At the same rate, how long will it take you to drive 450 miles?
Answer:
Given,
You drive 236 miles in 4.6 hours.
Speed = \(\frac { 236 }{ 4.6 } \) = 51.3043 miles per hour
The time takes to drive 450 miles = \(\frac { 450 }{ 51.3043 } \) = 8.8235
Lesson 4.1 Writing Equations in Slope-Intercept Form
Essential Question
Given the graph of a linear function, how can you write an equation of the line?
EXPLORATION 1
Writing Equations in Slope-Intercept Form
Work with a partner.
- Find the slope and y-intercept of each line.
- Write an equation of each line in slope-intercept form.
- Use a graphing calculator to verify your equation.
EXPLORATION 2

Mathematical Modeling
Work with a partner. The graph shows the cost of a smartphone plan.
a. What is the y-intercept of the line? Interpret the y-intercept in the context of the problem.
b. Approximate the slope of the line. Interpret the slope in the context of the problem.
c. Write an equation that represents the cost as a function of data usage.
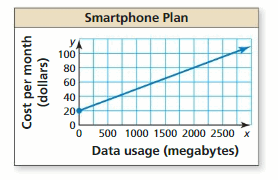
Communicate Your Answer
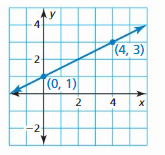
Question 3.
Given the graph of a linear function, how can you write an equation of the line?
Answer:
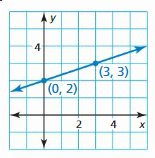
Let the ordered points (0, 2) and (3, 3) be (x1, y1) and (x2, y2) respectively.
m = (y2-y1)/(x2 – x1)
m = 3-2/3-0
m = 1/3
y = mx + c
y = 1/3x + 2
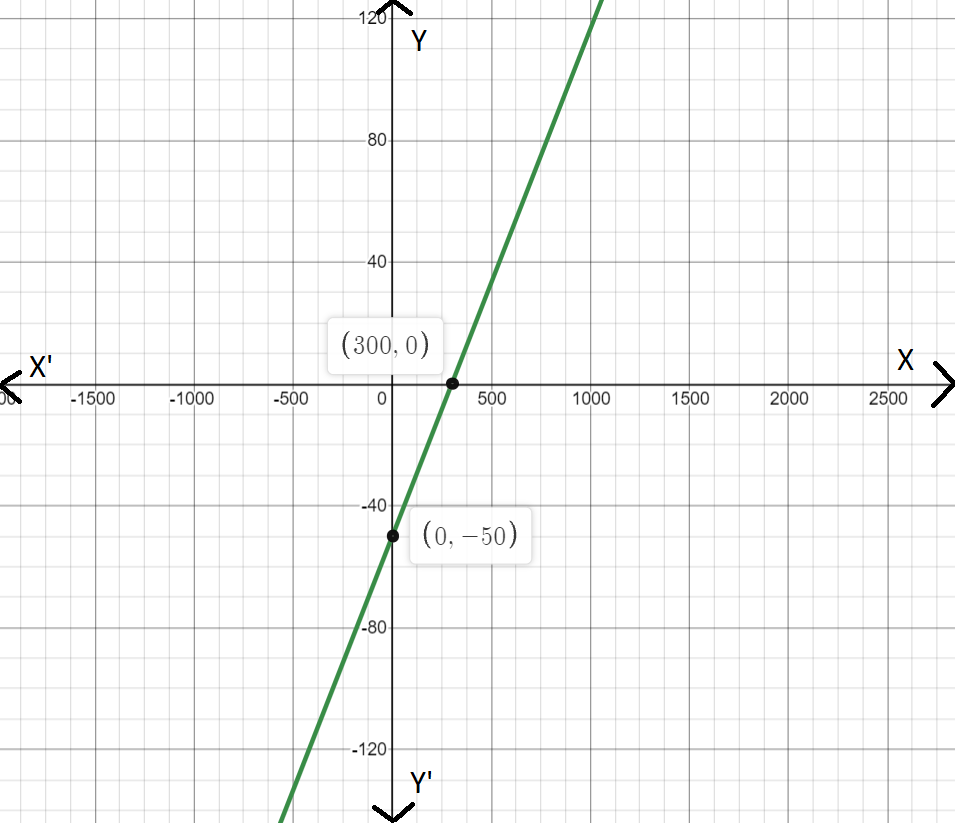
Question 4.
Give an example of a graph of a linear function that is different from those above. Then use the graph to write an equation of the line.
Answer:
The line passes through the points (0, -50), (300,0)
m = 0+50/300-0
m = 50/300
m = 1/6
c = -50
y = mx + c
y = 1/6x – 50
4.1 Lesson
Monitoring Progress
Write an equation of the line with the given slope and y-intercept.
Question 1.
slope = 7; y-intercept = 2
Answer:
The slope-intercept form of a line is y = mx + b
y = 7x + 2
Question 2.
slope = \(\frac{1}{3}\) ; y-intercept = -1
Answer:
The slope-intercept form of a line is y = mx + b
y = \(\frac{1}{3}\)x – 1
Write an equation of the line in slope-intercept form.
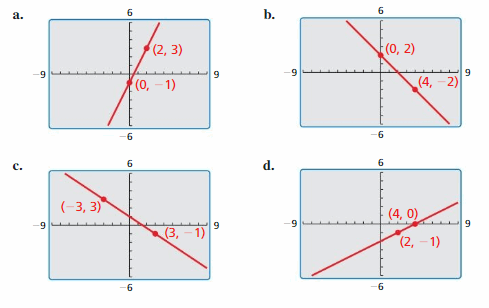
Question 3.
Answer:
Slope m = \(\frac { 3 – 1 }{ 4 – 0 } \) = \(\frac { 1 }{ 2 } \)
Because the line crosses the y-axis at (0, 1) the y-intercept is 1
The equation is y = \(\frac { 1 }{ 2 } \)x + 1
Question 4.
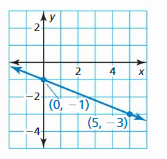
Answer:
Slope m = \(\frac { -3 + 1 }{ 5 – 0 } \) = \(\frac { -2 }{ 5 } \)
Because the line crosses the y-axis at (0, -1) the y-intercept is -1
The equation is y = \(\frac { -2 }{ 5 } \)x – 1
Question 5.
Write an equation of the line that passes through (0, -2) and (4, 10).
Answer:
Slope m = \(\frac { 10 + 2 }{ 4 – 0 } \) = 3
Because the line crosses the y-axis at (0, -2) the y-intercept is -2
The equation is y = 3x – 2
Question 6.
Write a linear function g with the values g(0) = 9 and g(8) = 7.
Answer:
(0, 9) and (8, 7) are the coordinates of points on a line
Slope m = \(\frac { 7 – 9 }{ 8 – 0 } \) = \(\frac { -1 }{ 4 } \)
Y-intercept is 9
The equation is y = \(\frac { -1 }{ 4 } \)x + 9
The linear function is g(x) = \(\frac { -1 }{ 4 } \)x + 9
Monitoring Progress
Question 7.
The corresponding data for electricity generated by hydropower are 248 million megawatt hours in 2007 and 277 million megawatt hours in 2012. Write a linear model that represents the number of megawatt hours generated by hydropower as a function of the number of years since 2007.
Answer:
Given,
The corresponding data for electricity generated by hydropower are 248 million megawatt hours in 2007 and 277 million megawatt hours in 2012.
Let x represents the time and y represents the number of megawatt-hours.
2007 corresponds to x = 0 and 2012 corresponds to x = 5
Let (x₁, y₁) = (0, 248) and (x₂, y₂) = (5, 277)
The y-intercept is 248.
Slope m = \(\frac { 277 – 248 }{ 5 – 0 } \)
= 5.8
Megawatt hours = initial value + rate of change • Years
y = 248 + 5.8 • x
y = 5.8x + 248
Writing Equations in Slope-Intercept Form 4.1 Exercises
Question 1.
COMPLETE THE SENTENCE
A linear function that models a real-life situation is called a __________.
Answer:
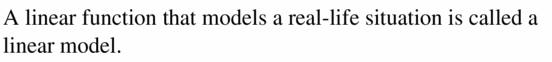
Question 2.
WRITING
Explain how you can use slope-intercept form to write an equation of a line given its slope and y-intercept.
Answer:
The equation of a line with the slope and y-intercept
y = mx + b
Substitute the value for the slope and y-intercept in the slope-intercept form to get the equation of the line.
Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, write an equation of the line with the given slope and y-intercept.
Question 3.
slope: 2
y-intercept: 9
Answer:
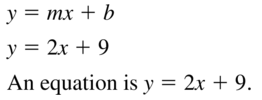
Question 4.
slope: 0
y-intercept: 5
Answer:
y = mx + b
y = 0x + 5
y = 5
Question 5.
slope: -3
y-intercept: 0
Answer:
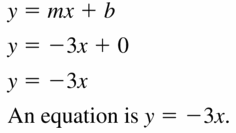
Question 6.
slope: -7
y-intercept: 1
Answer:
y = mx + b
y = -7x + 1
Question 7.
slope: \(\frac{2}{3}\)
y-intercept: -8
Answer:
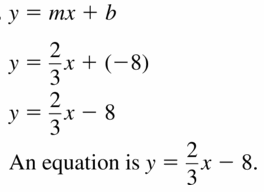
Question 8.
slope: –\(\frac{3}{4}\)
y-intercept: -6
Answer:
y = mx + b
y = –\(\frac{3}{4}\)x – 6
In Exercises 9–12, write an equation of the line in slope-intercept form.
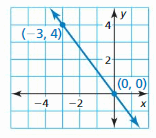
Question 9.
Answer:
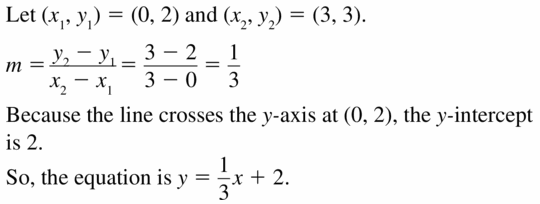
Question 10.
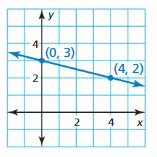
Answer:
Slope m = \(\frac { 3 – 2 }{ 0 – 4 } \)
= \(\frac { -1 }{ 4 } \)
The line crosses the y-axis at (0, 3), and the y-intercept is 3
y = \(\frac { -1 }{ 4 } \)x + 3
Question 11.
Answer:
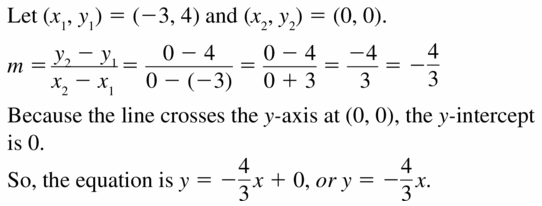
Question 12.
Answer:
Slope m = \(\frac { 2 + 2 }{ 2 – 0 } \) = 2
Because the line crosses the y-axis at (0, -2), the y-intercept is -2
y = 2x – 2
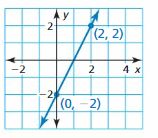
In Exercises 13–18, write an equation of the line that passes through the given points.
Question 13.
(3, 1), (0, 10)
Answer:
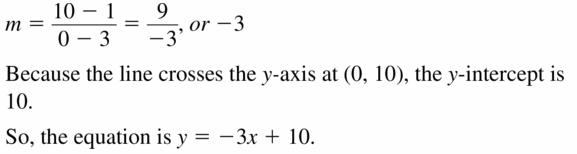
Question 14.
(2, 7), (0, -5)
Answer:
m = \(\frac { -5 – 7 }{ 0 – 2 } \) = 6
The line crosses the y-axis at (0, -5), and the y-intercept is -5
y = 6x – 5
Question 15.
(2, -4), (0, -4)
Answer:
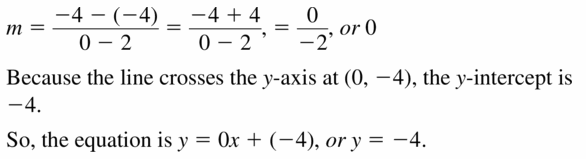
Question 16.
(-6, 0), (0, -24)
Answer:
m = \(\frac { -24 – 0 }{ 0 + 6 } \) = -4
The line crosses the y-axis at (0, -24), and the y-intercept is -24
y = -4x – 24
Question 17.
(0, 5), (-1.5, 1)
Answer:
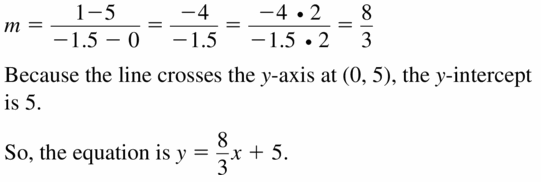
Question 18.
(0, 3), (-5, 2.5)
Answer:
m = \(\frac { 2.5 – 3 }{ -5 – 0 } \) = 0.1
The line crosses the y-axis at (0, 3), and the y-intercept is 3
y = 0.1x + 3
In Exercises 19–24, write a linear function f with the given values.
Question 19.
f(0) = 2, f(2) = 4
Answer:
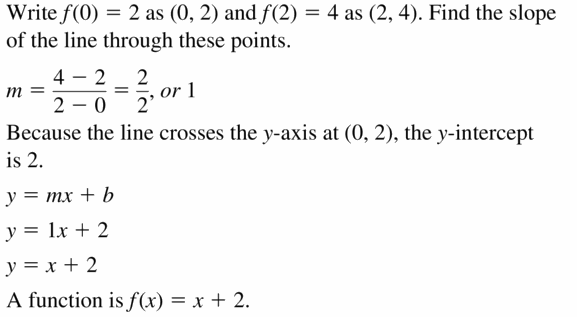
Question 20.
f(0) = 7, f(3) = 1
Answer:
f(0) = 7 is (0, 7) and f(3) = 1 is (3, 1)
m = \(\frac { 1 – 7 }{ 3 – 0 } \) = -2
The line crosses the y-axis at (0, 7), the y-intercept is 7
y = mx + b
y = -2x + 7
f(x) = -2x + 7
Question 21.
f(4) = -3, f(0) = -2
Answer:
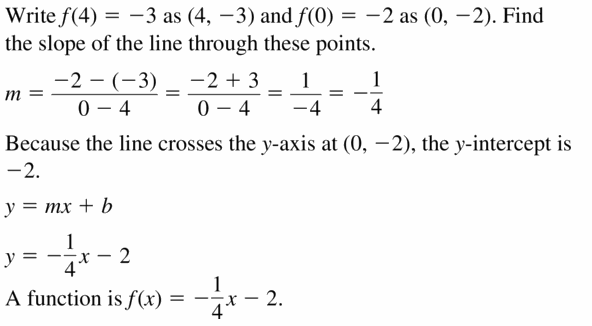
Question 22.
f(5) = -1, f(0) = -5
Answer:
f(5) = -1 is (5, -1) and f(0) = -5 is (0, -5)
m = \(\frac { -5 + 1 }{ 0 – 5 } \) = \(\frac { 4 }{ 5 } \)
The line crosses the y-axis at (0, -5), the y-intercept is -5
y = mx + b
y = \(\frac { 12 }{ 2 } \)x + -5
f(x) = \(\frac { 12 }{ 2 } \)x + -5
Question 23.
f(-2) = 6, f(0) = -4
Answer:
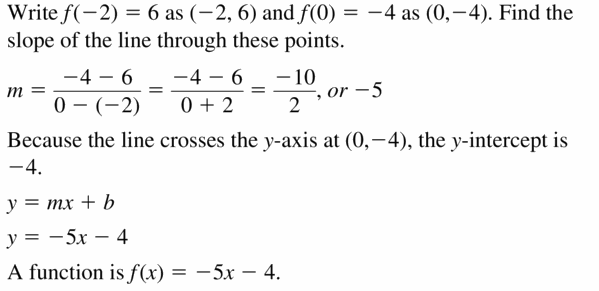
Question 24.
f(0) = 3, f(-6) = 3
Answer:
f(0) = 3 is (0, 3) and f(-6) = 3 is (-6, 3)
m = \(\frac { 3 – 3 }{ -6 – 0 } \) = 0
The line crosses the y-axis at (0, 3), the y-intercept is 3
y = mx + b
y = 0x + 3
y = 3
f(x) = 3
In Exercises 25 and 26, write a linear function f with the given values.
Question 25.
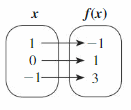
Answer:
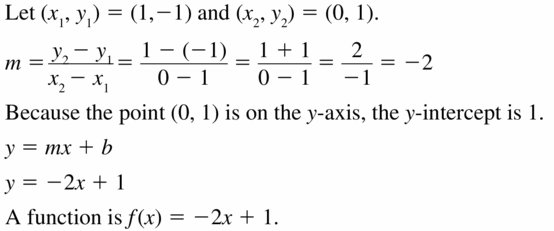
Question 26.
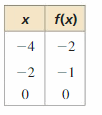
Answer:
The points are (-4, -2) and (-2, -1)
m = \(\frac { -1 + 2 }{ -2 + 4 } \) = \(\frac { 1 }{ 2 } \)
y = mx + b
y = \(\frac { 12 }{ 2 } \)x + b
The line passes through the point (0, 0)
0 = \(\frac { 12 }{ 2 } \)(0) + b
b = 0
y = \(\frac { 12 }{ 2 } \)x + 0
y = \(\frac { 12 }{ 2 } \)x
f(x) = \(\frac { 12 }{ 2 } \)x
Question 27.
ERROR ANALYSIS
Describe and correct the error in writing an equation of the line with a slope of 2 and a y-intercept of 7.
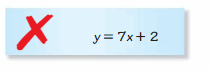
Answer:

Question 28.
ERROR ANALYSIS
Describe and correct the error in writing an equation of the line shown.
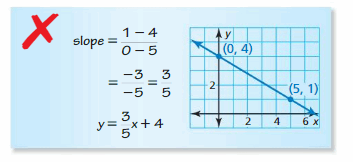
Answer:
m = \(\frac { 1 – 4 }{ 5 – 0 } \) = \(\frac { -3 }{ 5 } \)
y = \(\frac { -3 }{ 5 } \)x + 4
Question 29.
MODELING WITH MATHEMATICS
In 1960, the world record for the men’s mile was 3.91 minutes. In 1980, the record time was 3.81 minutes.
a. Write a linear model that represents the world record (in minutes) for the men’s mile as a function of the number of years since 1960.
b. Use the model to estimate the record time in 2000 and predict the record time in 2020.
Answer:

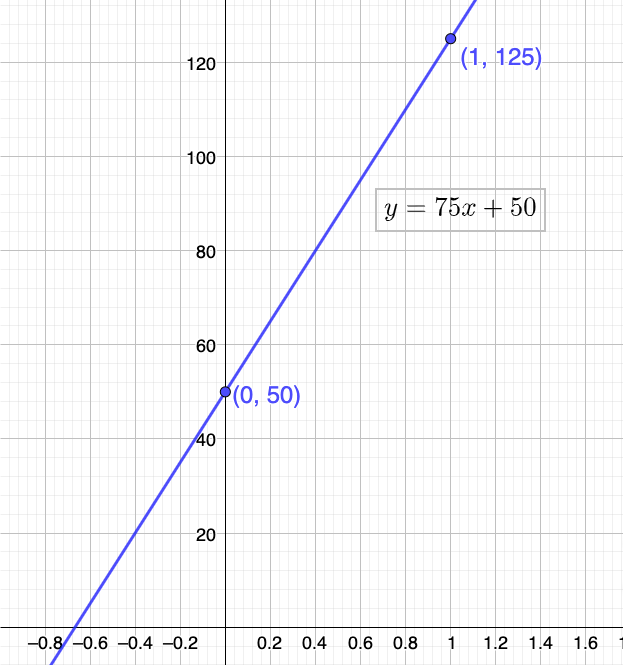
Question 30.
MODELING WITH MATHEMATICS
A recording studio charges musicians an initial fee of $50 to record an album. Studio time costs an additional $75 per hour.
a. Write a linear model that represents the total cost of recording an album as a function of studio time (in hours).
b. Is it less expensive to purchase 12 hours of recording time at the studio or a $750 music software program that you can use to record on your own computer? Explain.

Answer:
a. Let x be the time measured in hours, and y is the total cost in dollars
The slope-intercept form is y = mx + b
Let us consider that x = x₁ = 0 initially and the cost y = y₁ = $50. After 1 hour x₂ = 1, y₂ = 50 + 75 = 125
The line passes through points (0, 50) and (1, 125)
m = \(\frac { 125 – 50 }{ 1 – 0 } \) = 75 dollars per hour
y = 75x + 50
b. with the linear model it is possible to estimate the cost after t = 12 hours
y(12) = 75(12) + 50 = 950 dollars
Thus, it is less expensive to purchase music software.
Question 31.
WRITING
A line passes through the points (0, -2) and (0, 5). Is it possible to write an equation of the line in slope-intercept form? Justify your answer.
Answer:
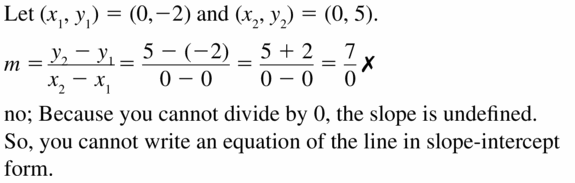
Question 32.
THOUGHT PROVOKING
Describe a real-life situation involving a linear function whose graph passes through the points.
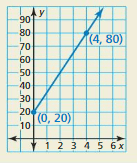
Answer:
Let us take x as the time and y as the distance covered.
A person starts jogging from 20 meters.
The person reaches 80 kilometers in 4 hours.
Question 33.
REASONING
Recall that the standard form of a linear equation is Ax + By = C. Rewrite this equation in slope-intercept form. Use your answer to find the slope and y-intercept of the graph of the equation -6x + 5y = 9.
Answer:

Question 34.
MAKING AN ARGUMENT
Your friend claims that given f(0) and any other value of a linear function f, you can write an equation in slope-intercept form that represents the function. Your cousin disagrees, claiming that the two points could lie on a vertical line. Who is correct? Explain.
Answer:
Your friend claims that given f(0) and any other value of a linear function f, you can write an equation in slope-intercept form that represents the function. Your cousin disagrees, claiming that the two points could lie on a vertical line.
We have f(0) we can find the y-intercept from it.
Another value of the linear function f can be used to find the slope.
The slope-intercept form y = mx + c
Thus my friend’s claim is correct.
Question 35.
ANALYZING A GRAPH
Line ℓ is a reflection in the x-axis of line k. Write an equation that represents line k.
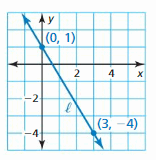
Answer:
Question 36.
HOW DO YOU SEE IT?
The graph shows the approximate U.S. box office revenues (in billions of dollars) from 2000 to 2012, where x = 0 represents the year 2000.
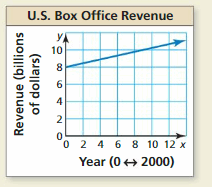
a. Estimate the slope and y-intercept of the graph.
b. Interpret your answers in part (a) in the context of the problem.
c. How can you use your answers in part (a) to predict the U.S. box office revenue in 2018?
Answer:
The points are(0, 8), (10, 10)
The slope m = \(\frac { 10 – 8 }{ 10 – 0 } \) = \(\frac { 1 }{ 5 } \)
The slope intercept form is y = \(\frac { 1 }{ 5 } \)x + 8
Question 37.
ABSTRACT REASONING
Show that the equation of the line that passes through the points (0, b) and (1, b + m) is y = mx + b. Explain how you can be sure that the point (-1, b – m) also lies on the line.
Answer:
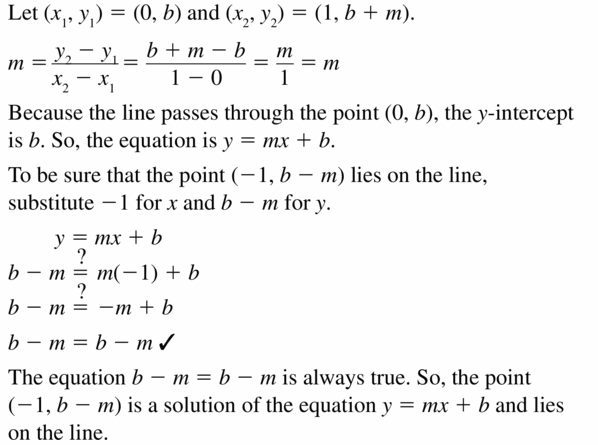
Maintaining Mathematical Proficiency
Solve the equation. (Section 1.3)
Question 38.
3(x – 15) = x + 11
Answer:
3(x – 15) = x + 11
3x – 45 = x + 11
3x – x = 11 + 45
2x = 56
x = 28
Question 39.
-4y – 10 = 4(y – 3)
Answer:
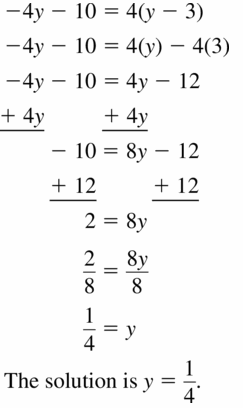
Question 40.
2(3d + 3) = 7 + 6d
Answer:
2(3d + 3) = 7 + 6d
6d + 6 = 7 + 6d
6d – 6d = 7 – 6
0 = 1
The equation is not correct.
Question 41.
-5(4 – 3n) = 10(n – 2)
Answer:
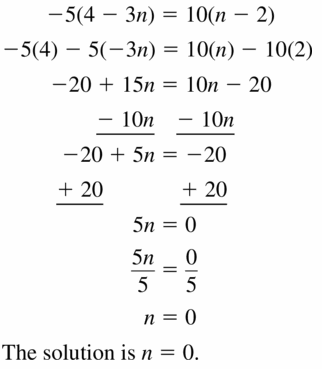
Use intercepts to graph the linear equation. (Section 3.4)
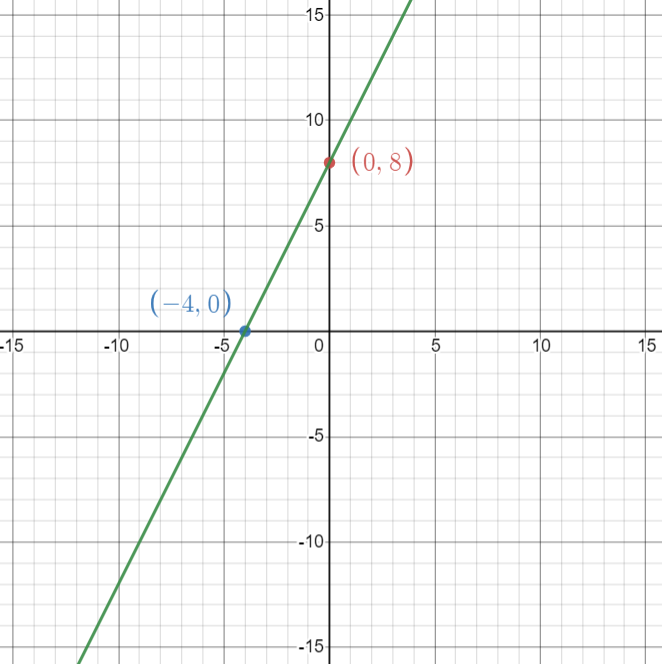
Question 42.
-4x + 2y = 16
Answer:
-4x + 2y = 16
Let x = 0
-4(0) + 2y = 16
2y = 16
y = 8
the y-intercept is 8
Let y = 0
-4x + 2(0) = 16
-4x = 16
x = -4
The x-intercept is -4.
Question 43.
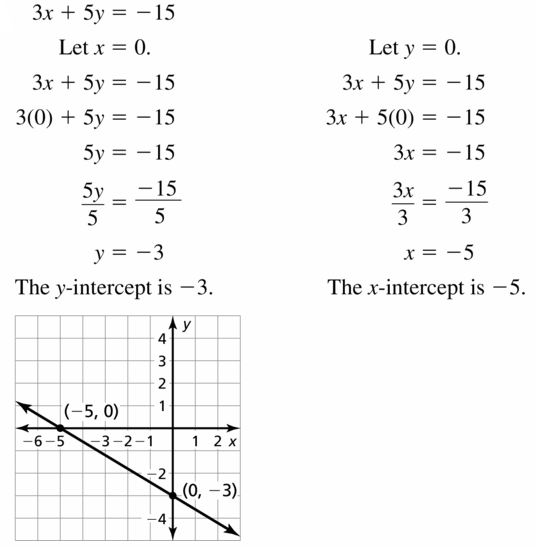
3x + 5y = -15
Answer:
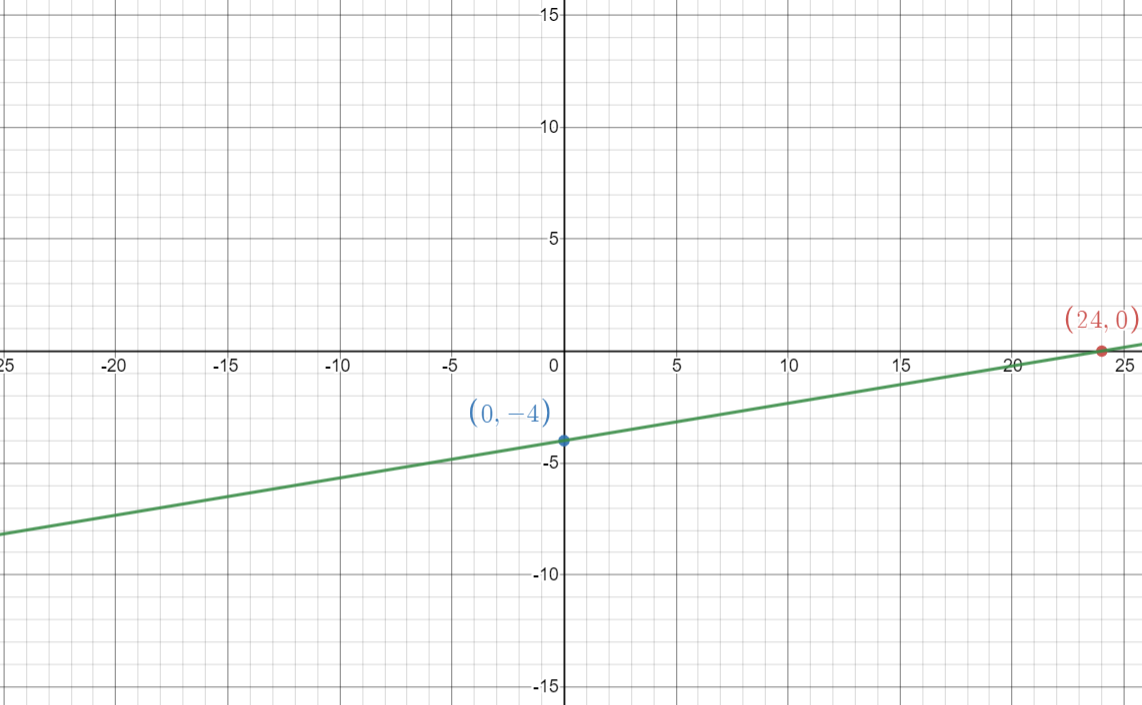
Question 44.
x – 6y = 24
Answer:
x – 6y = 24
Let y = 0
x – 6(0) = 24
x = 24
The x-intercept is 24
Let x = 0
0 – 6y = 24
y = -4
The y-intercept is -4
Question 45.
-7x – 2y = -21
Answer:
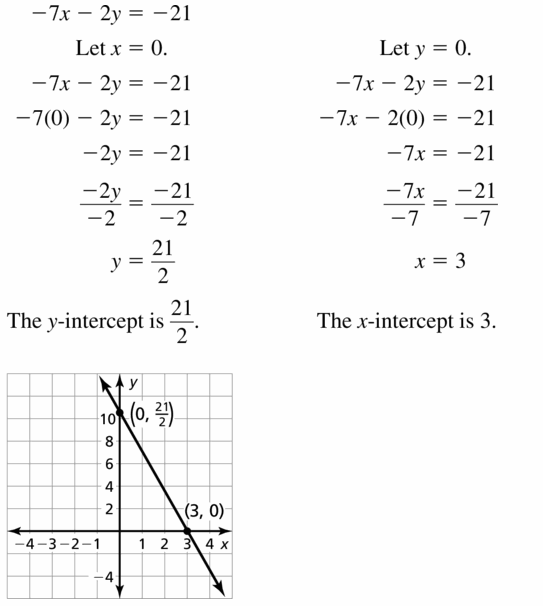
Lesson 4.2 Writing Equations in Point-Slope Form
Essential Question
How can you write an equation of a line when you are given the slope and a point on the line?
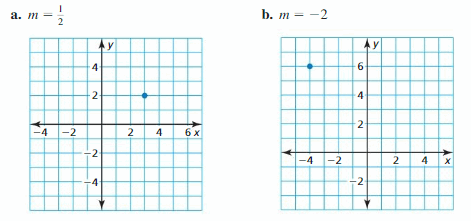
EXPLORATION 1
Writing Equations of Lines
Work with a partner.
- Sketch the line that has the given slope and passes through the given point.
- Find the y-intercept of the line.
- Write an equation of the line.
EXPLORATION 2
Writing a Formula
Work with a partner.
The point (x1, y1) is a given point on a nonvertical line. The point (x, y) is any other point on the line. Write an equation that represents the slope m of the line. Then rewrite this equation by multiplying each side by the difference of the x-coordinates to obtain the point-slope form of a linear equation.
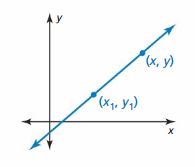
EXPLORATION 3
Writing an Equation
Work with a partner.
For four months, you have saved $25 per month. You now have $175 in your savings account.
a. Use your result from Exploration 2 to write an equation that represents the balance A after t months.
b. Use a graphing calculator to verify your equation.

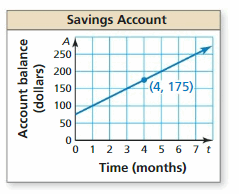
Communicate Your Answer
Question 4.
How can you write an equation of a line when you are given the slope and a point on the line?
Answer:
y = mx + b
Let slope be 2 and points be (-1, 4)
y = 2x + b
4 = 2(-1) + b
4 = -2 + b
b = 4 + 2
b = 6
Question 5.
Give an example of how to write an equation of a line when you are given the slope and a point on the line. Your example should be different from those above.
4.2 Lesson
Monitoring Progress
Write an equation in point-slope form of the line that passes through the given point and has the given slope.
Question 1.
(3, -1); m = -2
Answer:
The point-slope form of the line is (y – y₁) = m(x – x₁)
(y + 1) = -2(x – 3)
Question 2.
(4, 0); m = – \(\frac{2}{3}\)
Answer:
The point-slope form of the line is (y – y₁) = m(x – x₁)
(y – 0) = – \(\frac{2}{3}\)(x – 4)
y = – \(\frac{2}{3}\)(x – 4)
Write an equation in slope-intercept form of the line that passes through the given points.
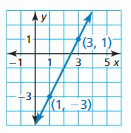
Question 3.
(1, 4), (3, 10)
Answer:
Slope m = \(\frac { 10 – 4 }{ 3 – 1 } \) = 3
Use slope, (1, 4) to write the equation
(y – 4) = 3(x – 1)
y – 4 = 3x – 3
y = 3x – 3 + 4
y = 3x + 1
Question 4.
(-4, -1), (8, -4)
Answer:
m = \(\frac { -4 + 1 }{ 8 + 4 } \) = \(\frac { -3 }{ 12 } \)
(y + 1) = \(\frac { -3 }{ 12 } \)(x + 4)
12(y + 1) = -3(x + 4)
12y + 12 = -3x – 12
12y = -3x – 24
y = \(\frac { -3 }{ 12 } \)x – 2
Question 5.
Write a linear function g with the values g(2) = 3 and g(6) = 5.
Answer:
The points are (2, 3) and (6, 5)
m = \(\frac { 5 – 3 }{ 6 – 2 } \) = \(\frac { 1 }{ 2 } \)
(y – 3) = \(\frac { 1 }{ 2 } \)(x – 2)
y = \(\frac { 1 }{ 2 } \)x – 1 + 3
y = \(\frac { 1 }{ 2 } \)x + 2
Question 6.
You pay an installation fee and a monthly fee for Internet service. The table shows the total cost for different numbers of months. Can the situation be modeled by a linear equation? Explain. If possible, write a linear model that represents the total cost as a function of the number of months.
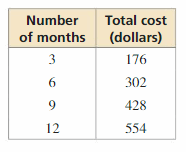
Answer:
The points are (3, 176), (6, 302)
Slope m = \(\frac { 302 – 176 }{ 6 – 3 } \) = \(\frac { 126 }{ 3 } \) = 42
Use slope, (3, 176) to write the equation
y – 176 = 42(x – 3)
y – 176 = 42x – 126
y = 42x + 50
Writing Equations in Point-Slope Form 4.2 Exercises
Vocabulary and Core Concept Check
Question 1.
USING STRUCTURE
Without simplifying, identify the slope of the line given by the equation y – 5 = -2(x + 5). Then identify one point on the line.
Answer:
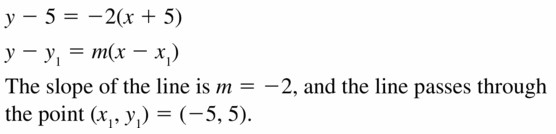
Question 2.
WRITING
Explain how you can use the slope formula to write an equation of the line that passes through (3, -2) and has a slope of 4.
Answer:
m = (y – y₁) = m(x – x₁)
(y + 2) = 4(x – 3)
y + 2 = 4x – 12
y = 4x – 14
Monitoring Progress and Modeling with Mathematics
In Exercises 3−10, write an equation in point-slope form of the line that passes through the given point and has the given slope.
Question 3.
(2, 1); m = 2
Answer:
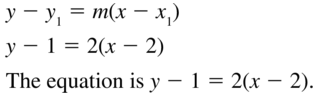
Question 4.
(3, 5); m = -1
Answer:
(y – y₁) = m(x – x₁)
y – 5 = -1(x – 3)
Question 5.
(7, -4); m = -6
Answer:
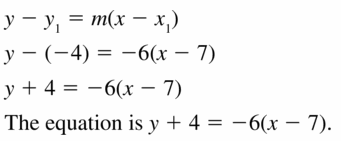
Question 6.
(-8, -2); m = 5
Answer:
(y – y₁) = m(x – x₁)
(y + 2) = 5(x + 8)
Question 7.
(9, 0); m = -3
Answer:
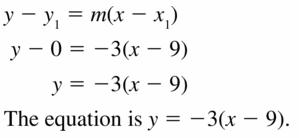
Question 8.
(0, 2); m = 4
Answer:
(y – y₁) = m(x – x₁)
(y – 2) = 4(x – 0)
y – 2 = 4x
Question 9.
(-6, 6); m – \(\frac{3}{2}\)
Answer:
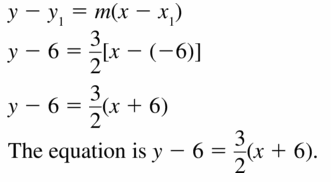
Question 10.
(5, -12); m = –\(\frac{2}{5}\)
Answer:
(y – y₁) = m(x – x₁)
(y + 12) = –\(\frac{2}{5}\)(x – 5)
In Exercises 11−14, write an equation in slope-intercept form of the line shown.
Question 11.
Answer:
Question 12.
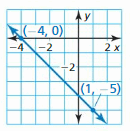
Answer:
(y – y₁) = m(x – x₁)
m = \(\frac { -5 – 0 }{ 1 + 4 } \) = -1
(y + 5) = -1(x – 1)
y + 5 = -x + 1
y = -x + 1 – 5
y = -x – 4
Question 13.
Answer:
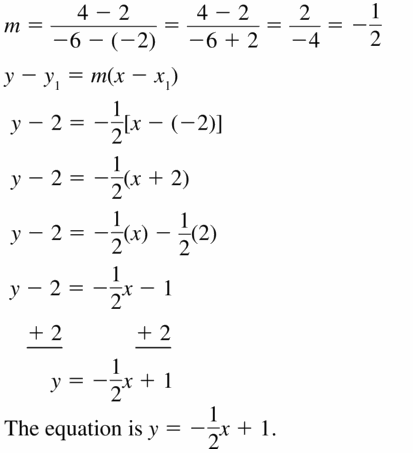
Question 14.
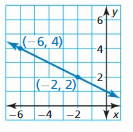
Answer:
(y – y₁) = m(x – x₁)
m = \(\frac { 1 – 4 }{ 4 – 8 } \) = \(\frac { 3 }{ 7 } \)
(y – 1) = \(\frac { 3 }{ 7 } \)(x – 4)
y – 1 = \(\frac { 3 }{ 7 } \)x – \(\frac { 12 }{ 7 } \)
y = \(\frac { 3 }{ 7 } \)x – \(\frac { 5 }{ 7 } \)
In Exercises 15−20, write an equation in slope-intercept form of the line that passes through the given points.
Question 15.
(7, 2), (2, 12)
Answer:
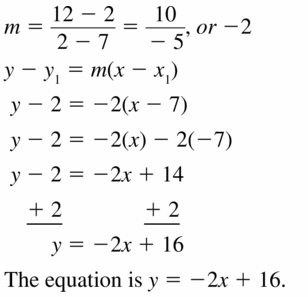
Question 16.
(6, -2), (12, 1)
Answer:
(y – y₁) = m(x – x₁)
m = \(\frac { 1 + 2 }{ 12 – 6 } \) = \(\frac { 1 }{ 2 } \)
(y – 1) = \(\frac { 1 }{ 2 } \)(x – 12)
y = \(\frac { 1 }{ 2 } \)x – 6 + 1
y = \(\frac { 1 }{ 2 } \)x – 5
Question 17.
(6, -1), (3, -7)
Answer:
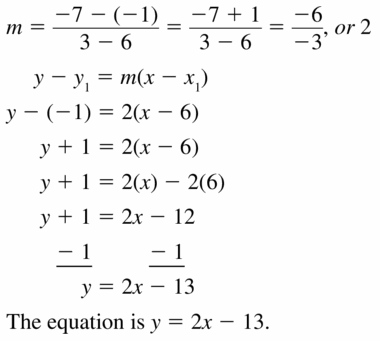
Question 18.
(-2, 5), (-4, -5)
Answer:
(y – y₁) = m(x – x₁)
m = \(\frac { -5 – 5 }{ -4 + 2} \) = 5
(y – 5) = 5(x + 2)
y = 5x + 10 + 5
y = 5x + 15
Question 19.
(1, -9), (-3, -9)
Answer:
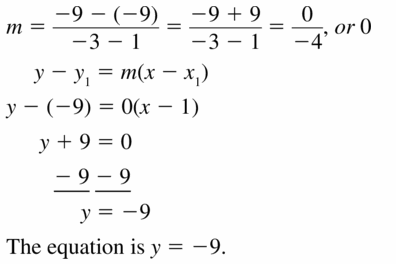
Question 20.
(-5, 19), (5, 13)
Answer:
m = \(\frac { 13 – 19 }{ 5 + 5 } \) = \(\frac { -3 }{ 5 } \)
(y – y₁) = m(x – x₁)
(y – 13) = \(\frac { -3 }{ 5 } \)(x – 5)
y = \(\frac { -3 }{ 5 } \)x + 3 + 13
y = \(\frac { -3 }{ 5 } \)x + 16
In Exercises 21−26, write a linear function f with the given values.
Question 21.
f(2) = -2, f(1) = 1
Answer:
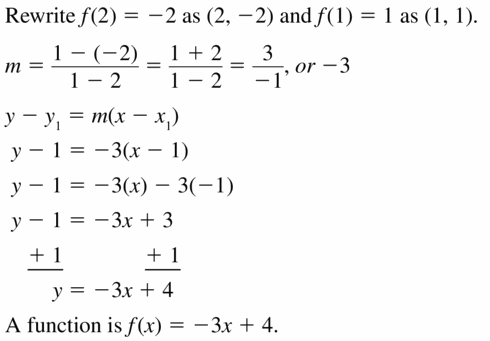
Question 22.
f(5) = 7, f(-2) = 0
Answer:
Rewrite f(5) = 7 as (5, -7),
f(-2) = 0 as (-2, 0)
m = \(\frac { 0 + 7 }{ -2 – 5 } \) = -1
(y – y₁) = m(x – x₁)
y + 7 = -1(x – 5)
y + 7 = -x + 5
y = -x + 5 – 7
y = -x – 2
Question 23.
f(-4) = 2, f(6) = -3
Answer:
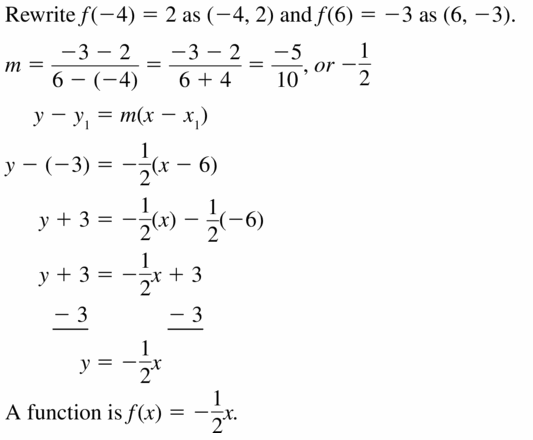
Question 24.
f(-10) = 4, f(-2) = 4
Answer:
Rewrite f(-10) = 4 as (-10, 4),
f(-2) = 4 as (-2, 4)
m = \(\frac { 4 – 4 }{ -2 + 10 } \) = 0
(y – y₁) = m(x – x₁)
y – 4 = 0(x + 2)
y = 4
Question 25.
f(-3) = 1, f(13) = 5
Answer:
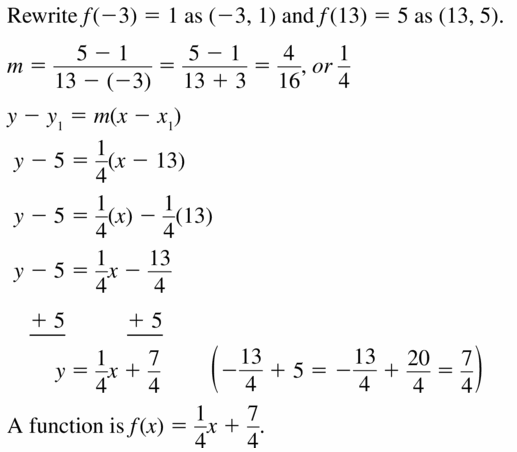
Question 26.
f(-9) = 10, f(-1) = -2
Answer:
Rewrite f(-9) = 10 as (-9, 10), f(-1) = -2 as (-1, -2)
m = \(\frac { -2 – 10 }{ -1 + 9 } \) = \(\frac { -3 }{ 2 } \)
(y – y₁) = m(x – x₁)
y + 2 = \(\frac { -3 }{ 2 } \)(x + 1)
y = \(\frac { -3 }{ 2 } \)x – \(\frac { 3 }{ 2 } \) – 2
y = \(\frac { -3 }{ 2 } \)x – \(\frac { 7 }{ 2 } \)
In Exercises 27−30, tell whether the data in the table can be modeled by a linear equation. Explain. If possible, write a linear equation that represents y as a function of x.
Question 27.
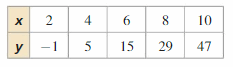
Answer:
Question 28.

Answer:
\(\frac { 10 – 16 }{ -1 + 3 } \) = -3, \(\frac { 4 – 10 }{ 1 + 1 } \) = -3
\(\frac { -2 – 4 }{ 3 – 1 } \) = -3
\(\frac { -8 + 2 }{ 5 – 3 } \) = -3
y – 16 = -3(x + 3)
y – 16 = -3x – 9
y = -3x – 9 + 16
y = -3x + 7
Question 29.
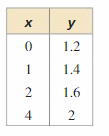
Answer:

Question 30.
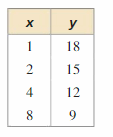
Answer:
\(\frac { 15 – 18 }{ 2 – 1 } \) = -3
\(\frac { 12 – 15 }{ 4 – 2 } \) = \(\frac { -3 }{ 2 } \)
\(\frac { 9 – 12 }{ 8 – 4 } \) = \(\frac { -3 }{ 4 } \)
Because the y values are not changing at a constant rate, the data cannot be modeled by a linear equation.
Question 31.
ERROR ANALYSIS
Describe and correct the error in writing a linear function g with the values g(5) = 4 and g(3) = 10.
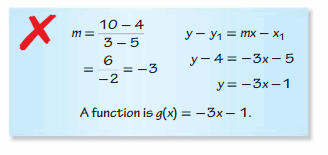
Answer:
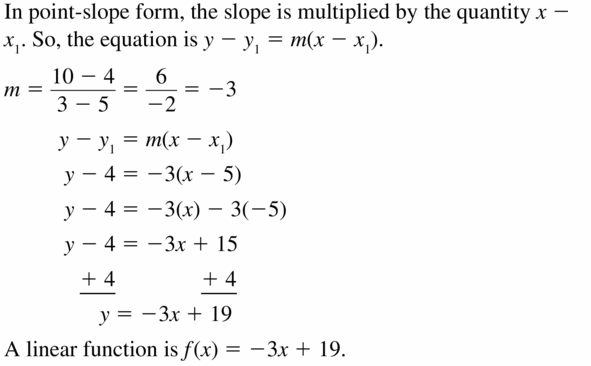
Question 32.
ERROR ANALYSIS
Describe and correct the error in writing an equation of the line that passes through the points (1, 2) and (4, 3).

Answer:
m = \(\frac { 3 – 2 }{ 4 – 1 } \) = \(\frac { 1 }{ 3 } \)
y – 2 = \(\frac { 1 }{ 3 } \)(x – 1)
Question 33.
MODELING WITH MATHEMATICS
You are designing a sticker to advertise your band. A company charges $225 for the first 1000 stickers and $80 for each additional 1000 stickers.
a. Write an equation that represents the total cost (in dollars) of the stickers as a function of the number (in thousands) of stickers ordered.
b. Find the total cost of 9000 stickers.
Answer:

Question 34.
MODELING WITH MATHEMATICS
You pay a processing fee and a daily fee to rent a beach house. The table shows the total cost of renting the beach house for different numbers of days.

a. Can the situation be modeled by a linear equation? Explain.
b. What is the processing fee? the daily fee?
c. You can spend no more than $1200 on the beach house rental. What is the maximum number of days you can rent the beach house?
Answer:
a. \(\frac { 450 – 246 }{ 4 – 2 } \) = 102
\(\frac { 654 – 450 }{ 6 – 4 } \) = 102
\(\frac { 858 – 654 }{ 8 – 6 } \) = 102
b. (y – 246) = 102(x – 2)
y – 246 = 102x – 204
y = 102x + 42
The processing fee is 42 and the daily fee is 102.
c. 102x + 42 < 1200
102x < 1158
x < 11.3
You can spend at least 11 days on the beach house rental for $1200
Question 35.
WRITING
Describe two ways to graph the equation y – 1 = \(\frac{3}{2}\)(x – 4).
Answer:


Question 36.
THOUGHT PROVOKING
The graph of a linear function passes through the point (12, -5) and has a slope of \(\frac{2}{5}\). Represent this function in two other ways.
Answer:
y + 5 = \(\frac{2}{5}\)(x – 12)
y + 5 = \(\frac{2}{5}\)x – \(\frac{24}{5}\)
y = \(\frac{2}{5}\)x – \(\frac{49}{5}\)
f(x) = \(\frac{2}{5}\)x – \(\frac{49}{5}\)
Question 37.
REASONING
You are writing an equation of the line that passes through two points that are not on the y-axis. Would you use slope-intercept form or point-slope form to write the equation? Explain.
Answer:

Question 38.
HOW DO YOU SEE IT? The graph shows two points that lie on the graph of a linear function.
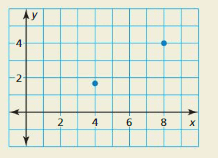
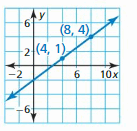
a. Does the y-intercept of the graph of the linear function appear to be positive or negative? Explain.
b. Estimate the coordinates of the two points. How can you use your estimates to confirm your answer in part (a)?
Answer:
a. Points are (4, 1.5), (8, 4)
m = \(\frac { 4 – 1.5 }{ 8 – 4 } \) = \(\frac { 2.5 }{ 4 } \)
y – 4 = \(\frac { 2.5 }{ 4 } \)(x – 8)
y = \(\frac { 2.5 }{ 4 } \)x – 5 + 4
y = \(\frac { 2.5 }{ 4 } \)x – 1
Question 39.
CONNECTION TO TRANSFORMATIONS
Compare the graph of y = 2x to the graph of y – 1 = 2(x + 3). Make a conjecture about the graphs of y = mx and y – k = m(x – h).
Answer:
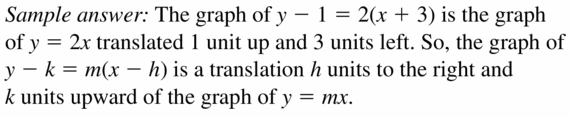
Question 40.
COMPARING FUNCTIONS
Three siblings each receive money for a holiday and then spend it at a constant weekly rate. The graph describes Sibling A’s spending, the table describes Sibling B’s spending, and the equation y = -22.5x + 90 describes Sibling C’s spending. The variable y represents the amount of money left after x weeks.
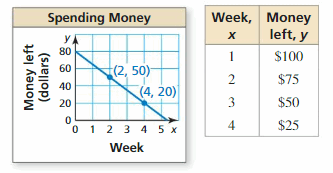
a. Which sibling received the most money? the least money?
b. Which sibling spends money at the fastest rate? the slowest rate?
c. Which sibling runs out of money first? last?
Answer:
m = \(\frac{20 – 50}{4 – 2}\) = -15
y – 20 = -15(x – 4)
y = -15x + 60 + 20
y = -15x + 80 is the sibling A spending
m = -25
y – 100 = -25(x – 1)
y = -25x + 25 + 100
y = -25x + 125 is the sibling B spending
y = -22.5x + 90 is sibling C spending
After 10 weeks,
Sibling A amount left is y = -15(10) + 80 = -70
Sibling B amount left is y = -25(10) + 125 = -125
Sibling C amount left is y = -22.5(10) + 90 = -135
Maintaining Mathematical Proficiency
Write the reciprocal of the number.
Question 41.
5
Answer:

Question 42.
-8
Answer:
The reciprocal of -8 is \(\frac { -1 }{ 8 } \)
Question 43.
–\(\frac{2}{7}\)
Answer:

Question 44.
\(\frac{3}{2}\)
Answer:
The reciprocal of \(\frac{3}{2}\) is \(\frac{2}{3}\)
Lesson 4.3 Writing Equations of Parallel and Perpendicular Lines
Essential Equation
How can you recognize lines that are parallel or perpendicular?
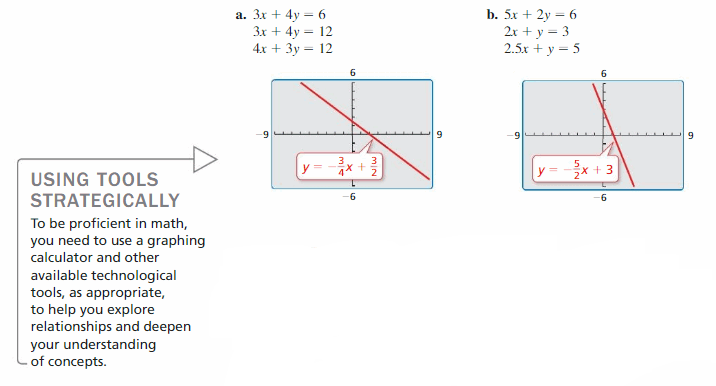
EXPLORATION 1
Recognizing Parallel Lines
Work with a partner. Write each linear equation in slope-intercept form. Then use a graphing calculator to graph the three equations in the same square viewing window. (The graph of the first equation is shown.) Which two lines appear parallel? How can you tell?
EXPLORATION 2
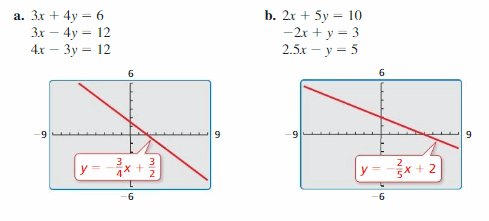
Recognizing Perpendicular Lines
Work with a partner. Write each linear equation in slope-intercept form. Then use a graphing calculator to graph the three equations in the same square viewing window. (The graph of the first equation is shown.) Which two lines appear perpendicular? How can you tell?
Communicate Your Answer
Question 3.
How can you recognize lines that are parallel or perpendicular?
Answer:
If the slopes of two lines are equal, then they are parallel lines.
If the slope of one line is the negative reciprocal of the second line, then the lines are perpendicular.
Question 4.
Compare the slopes of the lines in Exploration 1. How can you use slope to determine whether two lines are parallel? Explain your reasoning.
Answer:
Slopes are \(\frac { -3 }{ 4 } \), \(\frac { -5 }{ 2 } \)
The slopes are not equal.
So, the lines are not parallel.
Question 5.
Compare the slopes of the lines in Exploration 2. How can you use slope to determine whether two lines are perpendicular? Explain your reasoning.
Answer:
Slopes are \(\frac { -3 }{ 4 } \), \(\frac { -2 }{ 5 } \)
The slopes are not negative reciprocals.
Thus, the lines are not perpendicular.
4.3 Lesson
Question 1.
Line a passes through (-5, 3) and (-6, -1). Line b passes through (3, -2) and (2, -7). Are the lines parallel? Explain.
Answer:
Line a slope m = \(\frac { -1 – 3 }{ -6 + 5 } \) = 4
Line b slope M = \(\frac { -7 + 2 }{ 2 – 3 } \) = 5
The slopes are not equal.
The lines are not parallel
Question 2.
Write an equation of the line that passes through (-4, 2) and is parallel to the line y = \(\frac{1}{4}\)x + 1
Answer:
The line is parallel to y = \(\frac{1}{4}\)x + 1
The line slope is \(\frac{1}{4}\)
The equation of the line is (y – 2) = \(\frac{1}{4}\)(x + 4)
y = \(\frac{1}{4}\)x + 1 + 2
y = \(\frac{1}{4}\)x + 3
Monitoring Progress
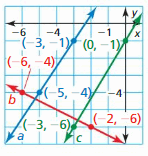
Question 3.
Determine which of the lines, if any, are parallel or perpendicular. Explain.
![]()
Answer:
Line a is 6y = -3 – 2x
y = \(\frac { -1 }{ 3 } \)x – \(\frac { 1 }{ 2 } \)
Slope is \(\frac { -1 }{ 3 } \)
line b slope is 3
line c is 18x – 9 = 6y
y = 3x – \(\frac { 3 }{ 2 } \)
m = 3
So, line b, c are parallel, and line a, b and a, c are perpendiculars.
Question 4.
Write an equation of the line that passes through (-3, 5) and is perpendicular to the line y = -3x – 1.
Answer:
The slope of a line perpendicular to y = -3x – 1 is \(\frac { 1 }{ 3 } \)
y – 5 = \(\frac { 1 }{ 3 } \)(x + 3)
y = \(\frac { 1 }{ 3 } \)x + 1 + 5
y = \(\frac { 1 }{ 3 } \)x + 6
Question 5.
In Example 5, a boat is traveling parallel to the shoreline and passes through (9, 3). Write an equation that represents the path of the boat.
Answer:
The boat is traveling parallel to the shoreline. So, the slope of the shoreline is \(\frac { -2 }{ 3 } \)
The equation of line is y – 3 = \(\frac { -2 }{ 3 } \)(x – 9)
y – 3 = \(\frac { -2 }{ 3 } \)x + 6
y = \(\frac { -2 }{ 3 } \)x + 9
Writing Equations of Parallel and Perpendicular Lines 4.3 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
Two distinct nonvertical lines that have the same slope are ____.
Answer:
![]()
Question 2.
VOCABULARY
Two lines are perpendicular. The slope of one line is –\(\frac{5}{7}\). What is the slope of the other line? Justify your answer.
Answer:
The slope of the perpendicular line is \(\frac{7}{5}\)
Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, determine which of the lines, if any, are parallel. Explain.
Question 3.
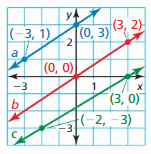
Answer:
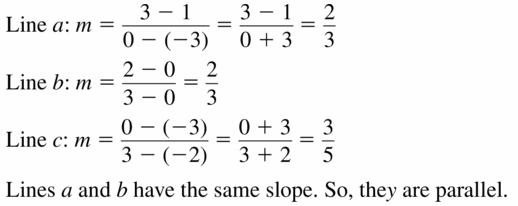
Question 4.
Answer:
Line a slope = \(\frac { 0 – 5 }{ 2 – 0 } \) = \(\frac { -5 }{ 2 } \)
Line b slope = \(\frac { 0 – 4 }{ 5 – 3 } \) = -2
Line c slope = \(\frac { 4 – 6 }{ 5 – 4 } \) = -2
Lines b , c are parallel
Question 5.
Line a passes through (-1, -2) and (1, 0).
Line b passes through (4, 2) and (2, -2).
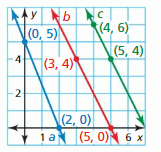
Line c passes through (0, 2) and (-1, 1).
Answer:
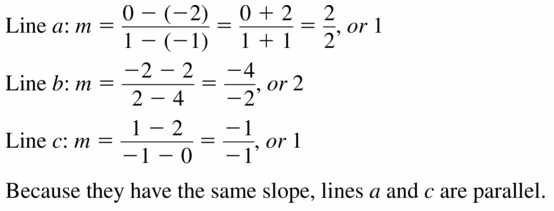
Question 6.
Line a passes through (-1, 3) and (1, 9).
Line b passes through (-2, 12) and (-1, 14).
Line c passes through (3, 8) and (6, 10).
Answer:
Line a slope = \(\frac { 9 – 3 }{ 1 + 1 } \) = 3
Line b slope = \(\frac { 14 – 12 }{ -1 + 2 } \) = 2
Line c slope = \(\frac { 10 – 8 }{ 6 – 3 } \) = \(\frac { 2 }{ 3 } \)
No lines are parallel. Because they have different slopes.
Question 7.
Line a: 4y + x = 8
Line b: 2y + x = 4
Line c: 2y = -3x + 6
Answer:
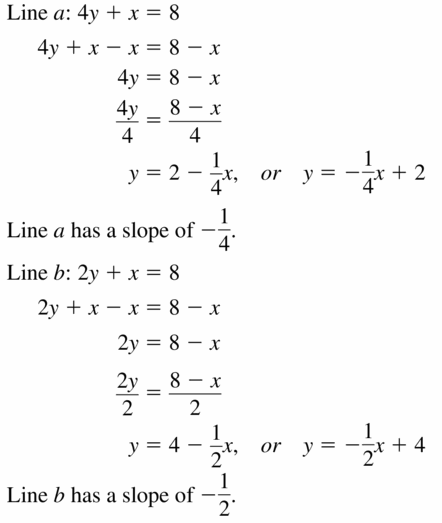
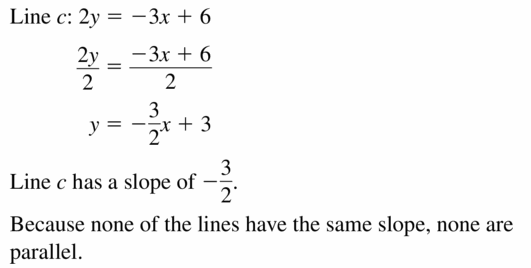
Question 8.
Line a: 3y – x = 6
Line b: 3y = x + 18
Line c: 3y – 2x = 9
Answer:
Line a slope = \(\frac { 1 }{ 3 } \)
Line b slope = \(\frac { 1 }{ 3 } \)
Line c slope = \(\frac { 2 }{ 3 } \)
Lines a, b are parallel. Because they have the same slope.
In Exercises 9–12, write an equation of the line that passes through the given point and is parallel to the given line.
Question 9.
(-1, 3); y = 2x + 2
Answer:
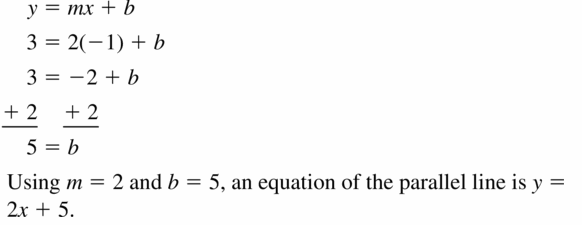
Question 10.
(1, 2); y = -5x + 4
Answer:
y = -5x + 4
m = -5
y – 2 = -5(x – 1)
y = -5x + 5 + 2
y = -5x + 7
Question 11.
(18, 2); 3y – x = -12
Answer:
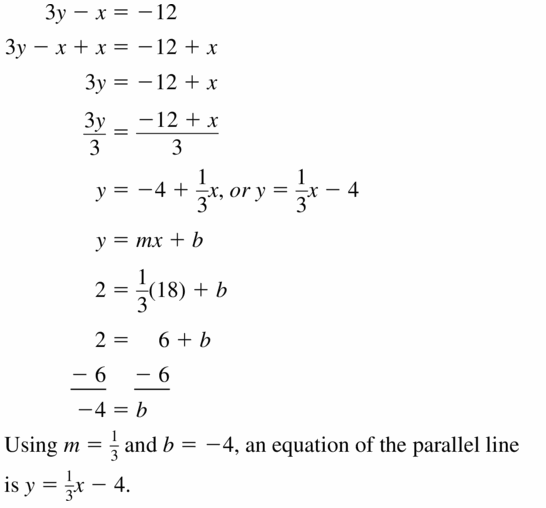
Question 12.
(2, -5); 2y = 3x + 10
Answer:
The slope of the line is \(\frac { 3 }{ 2 } \) as it is parallel to 2y = 3x + 10
y + 5 = \(\frac { 3 }{ 2 } \)(x – 2)
y = \(\frac { 3 }{ 2 } \)x – 3 – 5
y = \(\frac { 3 }{ 2 } \)x – 8
In Exercises 13–18, determine which of the lines, if any, are parallel or perpendicular. Explain.
Question 13.
Answer:
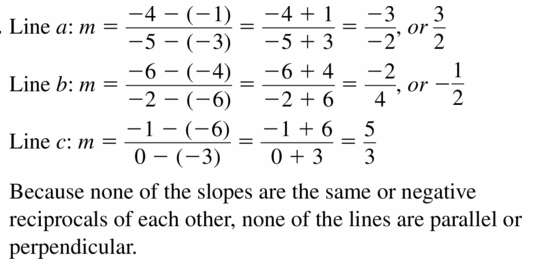
Question 14.
Answer:
Green line slope = \(\frac { 5 – 0 }{ 2 – 0 } \) = \(\frac { 5 }{ 2 } \)
Red line slope = \(\frac { 4 – 5 }{ 3 – 0 } \) = \(\frac { -1 }{ 3 } \)
Blue line slope = \(\frac { 0 – 1 }{ 2 + 1 } \) = \(\frac { -1 }{ 3 } \)
Red and blue lines are parallel as they have the same slope.
Question 15.
Line a passes through (-2, 1) and (0, 3).
Line b passes through (4, 1) and (6, 4).
Line c passes through (1, 3) and (4, 1).
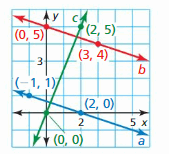
Answer:
Question 16.
Line a passes through (2, 10) and (4, 13).
Line b passes through (4, 9) and (6, 12).
Line c passes through (2, 10) and (4, 9).
Answer:
Line a slope = \(\frac { 13 – 10 }{ 4 – 2 } \) = \(\frac { 3 }{ 2 } \)
Line b slope = \(\frac { 12 – 9}{ 6 – 4 } \) = \(\frac { 3 }{ 2 } \)
Line c slope = \(\frac { 9 – 10 }{ 4 – 2 } \) = \(\frac { -1 }{ 2 } \)
Lines a, b are parallel as they have the same slope.
Question 17.
Line a: 4x – 3y = 2
Line b: y = \(\frac{4}{3}\)x + 2
Line c: 4y + 3x = 4
Answer:

Question 18.
Line a: y = 6x – 2
Line b: 6y = -x
Line c: y + 6x = 1
Answer:
Line a slope = 6
Line b slope = \(\frac { -1 }{ 6 } \)
Line c slope = -6
Lines a, b are perpendicular.
In Exercises 19–22, write an equation of the line that passes through the given point and is perpendicular to the given line.
Question 19.
(7, 10); y = \(\frac{1}{2}\)x – 9
Answer:
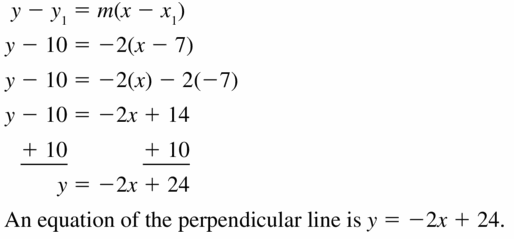
Question 20.
(-4, -1); y = \(\frac{4}{3}\)x + 6
Answer:
Slope of the given line is \(\frac{4}{3}\)
Slope of the perpendicular line is \(\frac{-3}{4}\)
Equation of the perpendicular line is (y + 1) = \(\frac{-3}{4}\)(x + 4)
y = \(\frac{-3}{4}\)x – 3 – 1
y = \(\frac{-3}{4}\)x – 4
Question 21.
(-3, 3); 2y = 8x – 6
Answer:
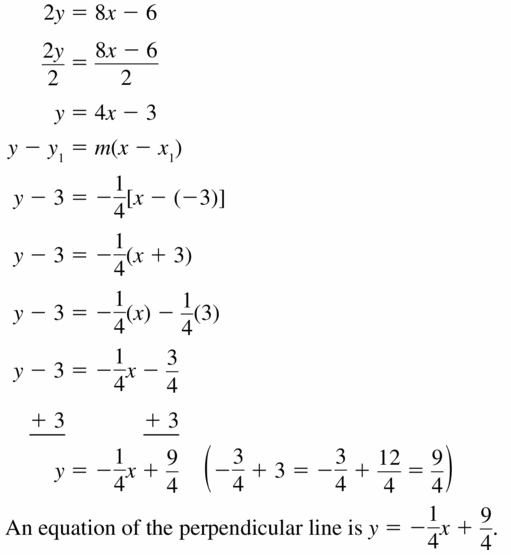
Question 22.
(8, 1); 2y + 4x = 12
Answer:
2y + 4x = 12
2y = -4x + 12
y = -2x + 6
The slope of the given line is -2
The slope of the perpendicular line is \(\frac { 1 }{ 2 } \)
The equation of the perpendicular line is (y – 1) = \(\frac { 1 }{ 2 } \)(x – 8)
y – 1 = \(\frac { 1 }{ 2 } \)x – 4
y = \(\frac { 1 }{ 2 } \)x – 3
In Exercises 23 and 24, write an equation of the line that passes through the given point and is (a) parallel and(b) perpendicular to the given line.
Question 23.
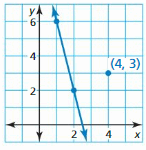
Answer:

Question 24.
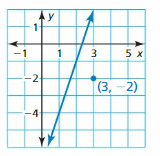
Answer:
The points on the line are (1, -4) and (2, -1)
The slope of the line = \(\frac { -1 + 4 }{ 2 – 1 } \) = 3
a. The slope of the parallel line is 3
y + 2 = 3(x – 3)
y = 3x – 9 – 2
y = 3x – 11
b. The slope of the perpendicular line is \(\frac { -1 }{ 3 } \)
y + 2 = \(\frac { -1 }{ 3 } \)(x – 3)
y = \(\frac { -1 }{ 3 } \)x + 1 – 2
y = \(\frac { -1 }{ 3 } \)x – 1
Question 25.
ERROR ANALYSIS
Describe and correct the error in writing an equation of the line that passes through (1, 3) and is parallel to the line y = \(\frac{1}{4}\)x + 2.
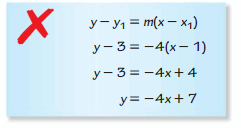
Answer:
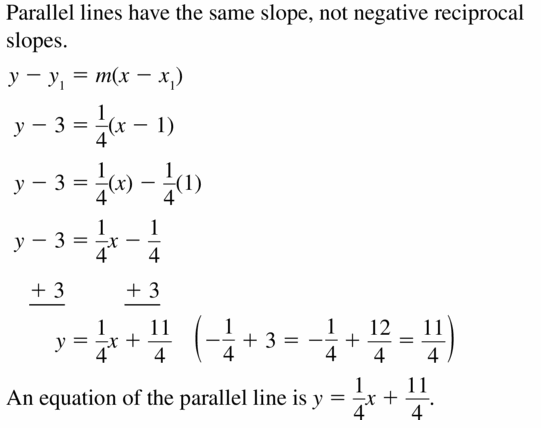
Question 26.
ERROR ANALYSIS
Describe and correct the error in writing an equation of the line that passes through (4, -5) and is perpendicular to the line y = \(\frac{1}{3}\)x + 5.
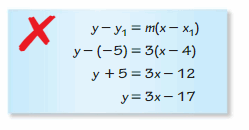
Answer:
m = -3
y + 5 = -3(x – 4)
y + 5 = -3x + 12
y = -3x + 12 – 5
y = -3x + 7
Question 27.
MODELING WITH MATHEMATICS
A city water department is proposing the construction of a new water pipe, as shown. The new pipe will be perpendicular to the old pipe. Write an equation that represents the new pipe.
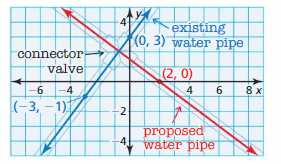
Answer:
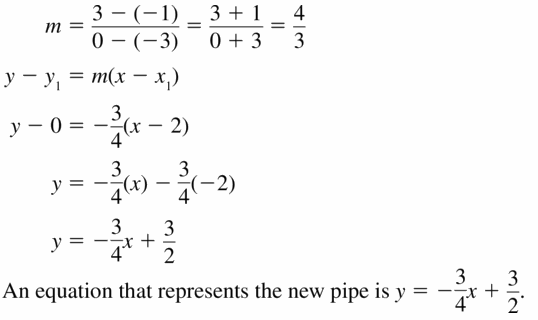
Question 28.
MODELING WITH MATHEMATICS
A parks and recreation department is constructing a new bike path. The path will be parallel to the railroad tracks shown and pass through the parking area at the point (4, 5). Write an equation that represents the path.
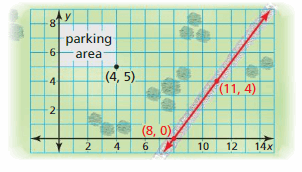
Answer:
The slope of line = \(\frac { 0 – 4 }{ 8 – 11 } \) = \(\frac { 4 }{ 3 } \)
The slope of the parallel line is \(\frac { 4 }{ 3 } \)
The equation of the line representing path is (y – 5) = \(\frac { 4 }{ 3 } \)(x – 4)
y – 5 = \(\frac { 4 }{ 3 } \)x – \(\frac { 16 }{ 3 } \)
y = \(\frac { 4 }{ 3 } \)x – \(\frac { 16 }{ 3 } \) + 5
y = \(\frac { 4 }{ 3 } \)x – \(\frac { 1 }{ 3 } \)
Question 29.
MATHEMATICAL CONNECTIONS
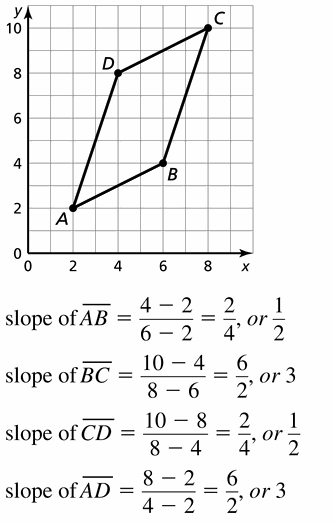
The vertices of a quadrilateral are A(2, 2), B(6, 4), C(8, 10), and D(4, 8).
a. Is quadrilateral ABCD a parallelogram? Explain.
b. Is quadrilateral ABCD a rectangle? Explain.
Answer:

Question 30.
USING STRUCTURE
For what value of a are the graphs of 6y = -2x + 4 and 2y = ax – 5 parallel? perpendicular?
Answer:
6y = -2x + 4
y = \(\frac { -1 }{ 3 } \)x + \(\frac { 2 }{ 3 } \)
The slope of first line is \(\frac { -1 }{ 3 } \)
Second line is 2y = ax – 5
y = \(\frac { a }{ 2 } \) – \(\frac { 5 }{ 2 } \)
Two lines are parallel means they have the same slope
\(\frac { a }{ 2 } \) = \(\frac { -1 }{ 3 } \)
a = \(\frac { -2 }{ 3 } \)
If \(\frac { a }{ 2 } \) = 3, then lines are perpendicular
a = 6
Question 31.
MAKING AN ARGUMENT
A hockey puck leaves the blade of a hockey stick, bounces off a wall, and travels in a new direction, as shown. Your friend claims the path of the puck forms a right angle. Is your friend correct? Explain.
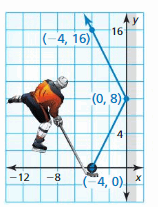
Answer:
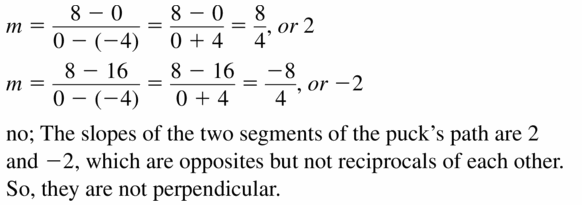
Question 32.
HOW DO YOU SEE IT?
A softball academy charges students an initial registration fee plus a monthly fee. The graph shows the total amounts paid by two students over a 4-month period. The lines are parallel.
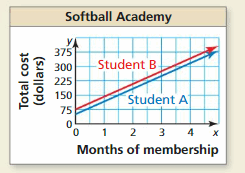
a. Did one of the students pay a greater registration fee? Explain.
b. Did one of the students pay a greater monthly fee? Explain.
Answer:
a. From the graph we can say that Student B paid a greater registration fee.
b. Yes, student B pays a greater monthly fee.
REASONING
In Exercises 33–35, determine whether the statement is always, sometimes, or never true. Explain your reasoning.
Question 33.
Two lines with positive slopes are perpendicular.
Answer:
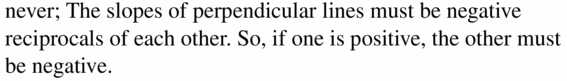
Question 34.
A vertical line is parallel to the y-axis.
Answer:
Always
The equation of the vertical line is in the form x = a, where a is any number.
The equation of the y-axis is x = 0
Therefore, the vertical line always parallel to the y-axis
Question 35.
Two lines with the same y-intercept are perpendicular.
Answer:

Question 36.
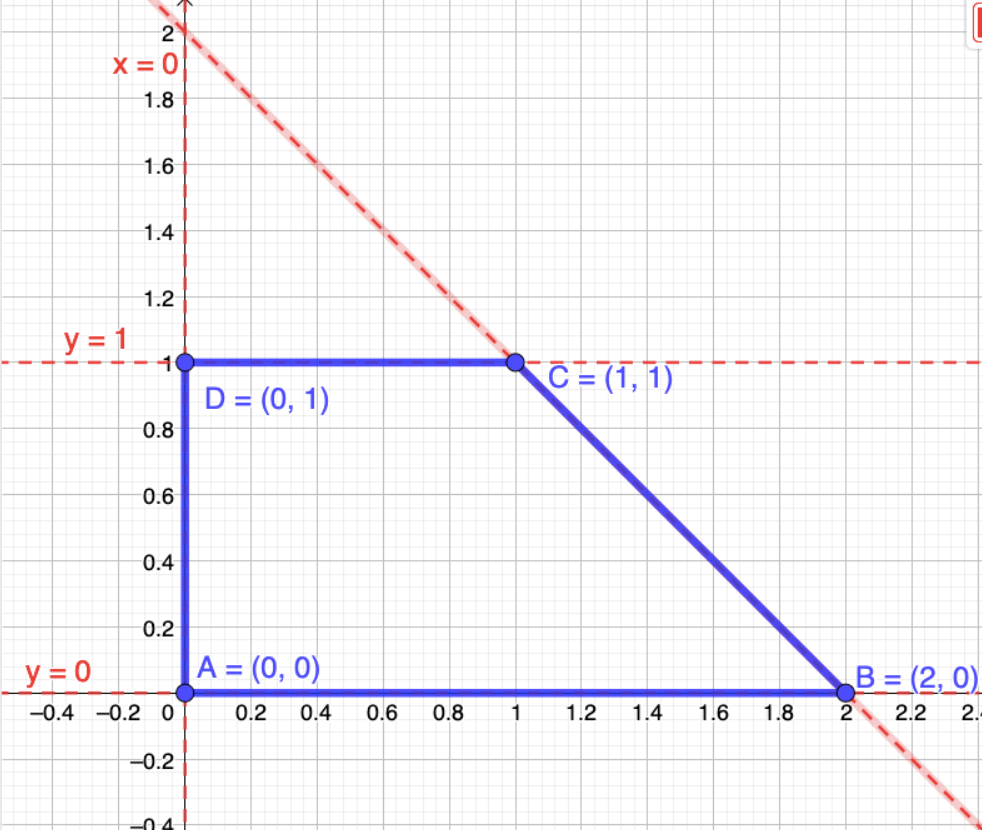
THOUGHT PROVOKING
You are designing a new logo for your math club. Your teacher asks you to include at least one pair of parallel lines and at least one pair of perpendicular lines. Sketch your logo in a coordinate plane. Write the equations of the parallel and perpendicular lines.
Answer:
Here, you can design a logo with a rectangle, a square, a diamond or with a simple trapezoid with a right angle. In the figure have been sketched a trapezoid with vertex at A(0, 0), B(0, 2), C(1, 1) and D(0, 1)
This quadrilateral has two parallel lines y = 0 and y = 1 and a vertex line x = 0 which is perpendicular to both horizontal lines.
Maintaining Mathematical Proficiency
Determine whether the relation is a function. Explain. (Section 3.1)
Question 37.
(3, 6), (4, 8), (5, 10), (6, 10), (7, 14)
Answer:
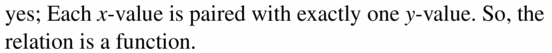
Question 38.
(-1, 6), (1, 4), (-1, 2), (1, 6), (-1, 5)
Answer:
Yes, each x-value is paired with exactly one y-value. So, the relation is a function.
Writing Linear Functions Study Skills: Getting Actively Involved in Class
4.1–4.3 What Did You Learn
Core Vocabulary

Core Concepts
Section 4.1
Using Slope-Intercept Form, p. 176
Section 4.2
Using Point-Slope Form, p. 182
Section 4.3
Parallel Lines and Slopes, p. 188
Perpendicular Lines and Slopes, p. 189
Mathematical Practices
Question 1.
How can you explain to yourself the meaning of the graph in Exercise 36 on page 180?
Answer:
The graph has tears on the x-axis and revenue on the y-axis. The graph represents approximate U.S box office revenues from 2000 to 2012.
Question 2.
How did you use the structure of the equations in Exercise 39 on page 186 to make a conjecture?
Answer:
Question 3.
How did you use the diagram in Exercise 31 on page 192 to determine whether your friend was correct?
Answer:
Study Skills
Getting Actively Involved in Class
If you do not understand something at all and do not even know how to phrase a question, just ask for clarification. You might say something like, “Could you please explain the steps in this problem one more time?”If your teacher asks for someone to go up to the board, volunteer. The student at the board often receives additional attention and instruction to complete the problem.

Writing Linear Functions 4.1 – 4.3
4.1 – 4.3 Quiz
Write an equation of the line in slope-intercept form. (Section 4.1)
Question 1.
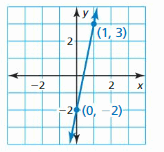
Answer:
Given points (1, 3) and (0, -2)
Slope = [y2-y1]/[x2-x1]
m = \(\frac { 3 + 2 }{ 1 – 0 } \) = 5
y = mx + b
3 = 5(1) + b
b = -2
The equation of the line is y = 5x – 2
Question 2.
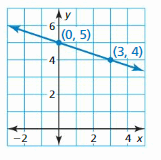
Answer:
Given points (0, 5) and (3, 4)
Slope = [y2-y1]/[x2-x1]
m = \(\frac { 5 – 4 }{ 0 – 3 } \) = \(\frac { -1 }{ 3 } \)
y = mx + b
5 = \(\frac { -1 }{ 3 } \)(0) + b
b = 5
The equation of the line is y = \(\frac { -1 }{ 3 } \)x + 5
Question 3.
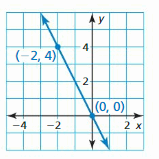
Answer:
Given points (-2, 4) and (0, 0)
Slope = [y2-y1]/[x2-x1]
m = \(\frac { 4 – 0 }{ -2 – 0 } \) = -2
y = mx + b
4 = -2(-2) + b
4 = 4 + b
b = 0
The equation of the line is y = -2x
Write an equation in point-slope form of the line that passes through the given points. (Section 4.2)
Question 4.
(-2, 5), (1, -1)
Answer:
Given points (-2, 5) and (1, -1)
Slope = [y2-y1]/[x2-x1]
Slope m = \(\frac { -1 – 5 }{ 1 + 2 } \) = -2
(y – y₁) = m(x – x₁)
y – 5 = -2(x + 2)
The equation is y – 5 = -2(x + 2)
Question 5.
(-3, -2), (2, -1)
Answer:
Given points (-3, -2) and (2, -1)
Slope = [y2-y1]/[x2-x1]
Slope m = \(\frac { -1 + 2 }{ 2 + 3 } \) = \(\frac { 1 }{ 5 } \)
(y – y₁) = m(x – x₁)
y + 2 = \(\frac { 1 }{ 5 } \)(x + 3)
The equation is y + 2 = \(\frac { 1 }{ 5 } \)(x + 3)
Question 6.
(1, 0), (4, 4)
Answer:
Given points (1, 0) and (4, 4)
Slope = [y2-y1]/[x2-x1]
Slope m = \(\frac { 4 – 1 }{ 4 – 0 } \) = \(\frac { 3 }{ 4 } \)
(y – y₁) = m(x – x₁)
y – 0 = \(\frac { 3 }{ 4 } \)(x – 1)
The equation is y – 0 = \(\frac { 3 }{ 4 } \)(x – 1)
Write a linear function f with the given values. (Section 4.1 and Section 4.2)
Question 7.
f(0) = 2, f(5) = -3
Answer:
Given,
f(0) = 2, f(5) = -3
Rewrite f(0) = 2 as (0, 2),
f(5) = -3 as (5, -3)
Slope m = \(\frac { -3 – 2 }{ 5 – 0 } \) = -1
(y – y₁) = m(x – x₁)
y – 2 = -1(x – 0)
y – 2 = -x
y = -x + 2
f(x) = 2 – x
Question 8.
f(-1) = -6, f(4) = -6
Answer:
Given,
f(-1) = -6, f(4) = -6
Rewrite f(-1) = -6 as (-1, 6), f(4) = -6 as (4, -6)
Slope = [y2-y1]/[x2-x1]
m = \(\frac { -6 – 6 }{ 4 + 1 } \) = \(\frac { -12 }{ 5 } \)
(y – y₁) = m(x – x₁)
y – 6 = \(\frac { -12 }{ 5 } \)(x + 1)
y = \(\frac { -12 }{ 5 } \)x – \(\frac { 12 }{ 5 } \) + 6
y = \(\frac { -12 }{ 5 } \)x + \(\frac { 18 }{ 5 } \)
f(x) = \(\frac { -12 }{ 5 } \)x + \(\frac { 18 }{ 5 } \)
Question 9.
f(-3) = -2, f(-2) = 3
Answer:
Given,
f(-3) = -2, f(-2) = 3
Rewrite f(-3) = -2 as (-3, 2), f(-2) = 3 as (-2, 3)
Slope = [y2-y1]/[x2-x1]
m = \(\frac { 3 – 2}{ -2 + 3 } \) = 1
(y – y₁) = m(x – x₁)
y – 2 = 1(x + 3)
y = x + 3 + 2
y = x + 5
f(x) = x + 5
Determine which of the lines, if any, are parallel or perpendicular. Explain. (Section 4.3)
Question 10.
Line a passes through (-2, 2) and (2, 1).
Line b passes through (1, -8) and (3, 0).
Line c passes through (-4, -3) and (0, -2).
Answer:
Given,
Line a passes through (-2, 2) and (2, 1)
Line b passes through (1, -8) and (3, 0)
Line c passes through (-4, -3) and (0, -2)
Line a slope = \(\frac { 1 – 2 }{ 2 + 2 } \) = \(\frac { -1 }{ 4 } \)
Line b slope = \(\frac { 0 + 8 }{ 3 – 1 } \) = 4
Line c slope = \(\frac { -2 + 3 }{ 0 + 4 } \) = \(\frac { 1 }{ 4 } \)
Lines a, and b are perpendicular as their slopes are negative reciprocals.
Question 11.
Line a: 2x + 6y = -12
Line b: y = \(\frac{3}{2}\)x – 5
Line c : 3x – 2y = -4
Answer:
Given,
Line a: 2x + 6y = -12
Line b: y = \(\frac{3}{2}\)x – 5
Line c : 3x – 2y = -4
6y = -2x – 12
y = \(\frac { -1 }{ 3 } \)x – 2
Line a slope = \(\frac { -1 }{ 3 } \)
Line b slope = \(\frac{3}{2}\)
3x + 4 = 2y
y = \(\frac{3}{2}\)x + 2
Line c slope = \(\frac{3}{2}\)
Lines b, c are parallel.
Write an equation of the line that passes through the given point and is (a) parallel and (b) perpendicular to the given line. (Section 4.3)
Question 12.
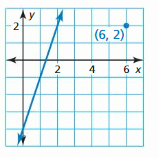
Answer:
Given,
The points on the lines are (1, -1), (2, 2)
Slope = [y2-y1]/[x2-x1]
Slope of the line = \(\frac { 2 + 1 }{ 2 – 1 } \) = 3
The slope of the parallel line is 3
Equation of parallel line is y – 2 = 3(x – 6)
y = 3x – 18 + 2
y = 3x – 16
Slope of the perpendicular line is \(\frac { -1 }{ 3 } \)
Equation of the perpendicular line is y – 2 = \(\frac { -1 }{ 3 } \)(x – 6)
y = \(\frac { -1 }{ 3 } \)x + 2 + 2
y = \(\frac { -1 }{ 3 } \)x + 4
Question 13.
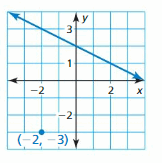
Answer:
The points on the lines are (2, 1), (-2, 3)
Slope = [y2-y1]/[x2-x1]
Slope of the line = \(\frac { 3 – 1 }{ -2 – 2 } \) = \(\frac { -1 }{ 2 } \)
Slope of the parallel line is \(\frac { -1 }{ 2 } \)
Equation of parallel line is y + 3 = \(\frac { -1 }{ 2 } \)(x + 2)
y = \(\frac { -1 }{ 2 } \)x – 1 – 3
y = \(\frac { -1 }{ 2 } \) – 4
The slope of the perpendicular line is 2
Equation of the perpendicular line is y + 3 = 2(x + 2)
y + 3 = 2x + 4
y = 2x + 4 – 3
y = 2x + 1
Question 14.
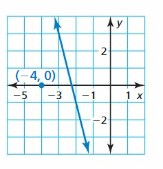
Answer:
Given,
The points on the lines are (-3, 3), (-2, -1)
Slope = [y2-y1]/[x2-x1]
Slope of the line = \(\frac { -1 – 3 }{ -2 + 3 } \) = -4
Slope of the parallel line is -4
Equation of parallel line is y – 0 = -4(x + 4)
y = -4x – 16
Slope of the perpendicular line is \(\frac { 1 }{ 4 } \)
Equation of the perpendicular line is y – 0 = \(\frac { 1 }{ 4 } \)(x + 4)
y = \(\frac { 1 }{ 4 } \)x + 1
Question 15.
A website hosting company charges an initial fee of $48 to set up a website. The company charges $44 per month to maintain the website. (Section 4.1)
a. Write a linear model that represents the total cost of setting up and maintaining a website as a function of the number of months it is maintained.
b. Find the total cost of setting up a website and maintaining it for 6 months.
c. A different website hosting company charges $62 per month to maintain a website, but there is no initial set-up fee. You have $620. At which company can you set up and maintain a website for the greatest amount of time? Explain.
Answer:
a. Let y be the cost
Let x be the number of months
Since the company charges 44 per month
Slope of the line is m = 44
Since the company charges an initial fee of 48,
y-intercept is b = 48
Use the slope-intercept formula
y = 44x + 48
The linear model that represents the total cost is y = 44x + 48
b. To find the total cost for 6 months
x = 6
y = 44(6) + 48
y = 312
The total cost for 6 months is $312.
c. Since you have $620
y = 620
y = 44x + 48
620 = 44x + 48
x = 13
The first company with an initial fee of $48 and $44 per month can set up and maintain a website for 13 months
y = 62x
620 = 62x
x = 10
The second company with a charge of $62 per month can set up and maintain a website for 10 months.
Question 16.
The table shows the amount of water remaining in a water tank as it drains. Can the situation be modeled by a linear equation? Explain. If possible, write a linear model that represents the amount of water remaining in the tank as a function of time. (Section 4.2)
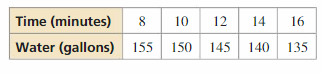
Answer:
The table shows the amount of water remaining in a water tank as it drains.
\(\frac { 150 – 155 }{ 10 – 8 } \) = \(\frac { -5 }{ 2 } \)
\(\frac { 145 – 150 }{ 12 – 10 } \) = \(\frac { -5 }{ 2 } \)
\(\frac { 140 – 145 }{ 14 – 12 } \) = \(\frac { -5 }{ 2 } \)
\(\frac { 135 – 140 }{ 6 – 14 } \) = \(\frac { -5 }{ 2 } \)
So, the data can be modeled by a linear equation
m = \(\frac { -5 }{ 2 } \)
y – 155 = \(\frac { -5 }{ 2 } \)(x – 8)
y = \(\frac { -5 }{ 2 } \)x + 4 + 155
y = \(\frac { -5 }{ 2 } \)x + 159
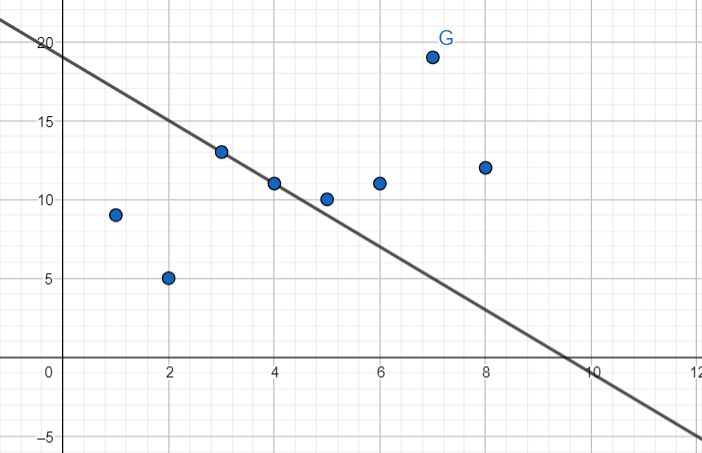
Lesson 4.4 Scatter Plots and Lines of Fit
Essential Question
How can you use a scatter plot and a line of fit to make conclusions about data?
Answer:
A scatter plot is a graph that shows the relationship between two data sets. The two data sets are graphed as ordered pairs in a coordinate plane. We use a scatter plot and a line of fit to make conclusions about data values not in the original data set.
EXPLORATION 1
Finding a Line of Fit
Work with a partner. A survey was taken of 179 married couples. Each person was asked his or her age. The scatter plot shows the results.
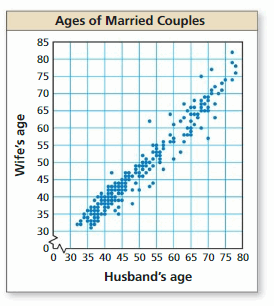
a. Draw a line that approximates the data. Write an equation of the line. Explain the method you used.
b. What conclusions can you make from the equation you wrote? Explain your reasoning.

EXPLORATION 2
Work with a partner. The scatter plot shows the median ages of American women at their first marriage for selected years from 1960 through 2010.
a. Draw a line that approximates the data. Write an equation of the line. Explain the method you used.
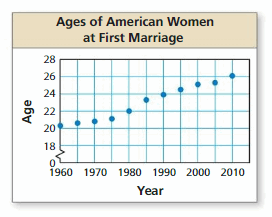
b. What conclusions can you make from the equation you wrote?
c. Use your equation to predict the median age of American women at their first marriage in the year 2020.
Communicate Your Answer
Question 3.
How can you use a scatter plot and a line of fit to make conclusions about data?
Answer:
A scatter plot is a graph that shows the relationship between two data sets. The two data sets are graphed as ordered pairs in a coordinate plane. We use a scatter plot and a line of fit to make conclusions about data values not in the original data set.
Question 4.
Use the Internet or some other reference to find a scatter plot of real-life data that is different from those given above. Then draw a line that approximates the data and write an equation of the line. Explain the method you used.
4.4 Lesson
Monitoring Progress
Question 1.
How many calories are in the smoothie that contains 51 grams of sugar?
Answer:
Draw a horizontal line from the point that has an x-value of 51. It crosses the y-axis at 260
Thus, 51 grams of sugar has 260 calories.
Question 2.
How many grams of sugar are in the smoothie that contains 250 calories?
Answer:
Draw a vertical line from the point that has a y-value of 250. It crosses the x-axis at 55.
Thus, the smoothie has 55 grams of sugar.
Make a scatter plot of the data. Tell whether the data show a positive, a negative, or no correlation.
Question 3.

Answer:
The number of attendees increases as the average temperature increases.
The scatter plot shows a positive correlation.
Question 4.

Answer:
As the age of the car increases its value decreases.
The scatter plot shows a negative correlation.
Question 5.
The following data pairs show the monthly income x (in dollars) and the monthly car payment y (in dollars) of six people: (2100, 410), (1650, 315), (1950, 405), (1500, 295), (2250, 440), and (1800, 375). Write an equation that models the monthly car payment as a function of the monthly income. Interpret the slope and y-intercept of the line of fit.
Answer:
m = [y2-y1]/[x2-x1]
slope = (440-410)/(2250-2100)
m = 1/5
m = 1/4 = (y – 440)/(x – 2250)
4y – 1760 = x – 2250
4y = x – 490
y = (1/4)x – 122.5
So, the slope and y-intercept are 1/4 and -122.5 respectively.
Scatter Plots and Lines of Fit 4.4 Exercises
Question 1.
COMPLETE THE SENTENCE
When data show a positive correlation, the dependent variable tends to ____________ as the independent variable increases.
Answer: When data show a positive correlation, the dependent variable tends to increase as the independent variable increases.
Question 2.
VOCABULARY
What is a line of fit?
Answer:
A line of best fit is a straight line that minimizes the distance between it and some data. The line of best fit is used to express a relationship in a scatter plot of different data points.
Monitoring Progress and Modeling with Mathematics
In Exercises 3–6, use the scatter plot to fill in the missing coordinate of the ordered pair.
Question 3.
![]()
Answer:
![]()
Question 4.
![]()
Answer:
(3, 14)
Question 5.
![]()
Answer:
![]()
Question 6.
![]()
Answer:
(8, 17)
Question 7.
INTERPRETING A SCATTER PLOT
The scatter plot shows the hard drive capacities (in gigabytes) and the prices (in dollars) of 10 laptops.
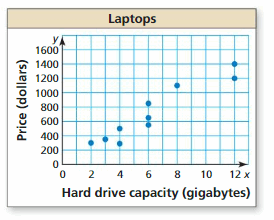
a. What is the price of the laptop with a hard drive capacity of 8 gigabytes?
b. What is the hard drive capacity of the $1200 laptop?
c. What tends to happen to the price as the hard drive capacity increases?
Answer:

Question 8.
INTERPRETING A SCATTER PLOT
The scatter plot shows the earned run averages and the winning percentages of eight pitchers on a baseball team.
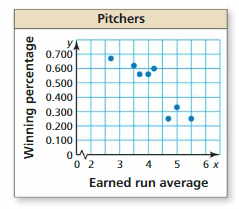
a. What is the winning percentage of the pitcher with an earned run average of 4.2?
b. What is the earned run average of the pitcher with a winning percentage of 0.33?
c. What tends to happen to the winning percentage as the earned run average increases?
Answer:
a. 0.600 is the winning percentage of the pitcher with an earned run average of 4.2
b. 5 is the earned run average of the pitcher with a winning percentage of 0.33
c. As earned run average increases the winning percentage decreases.
In Exercises 9–12, tell whether x and y show a positive, a negative, or no correlation.
Question 9.
Answer:

Question 10.
Answer:
The y-value tends to increase as the x-values increase.
The scatter plot shows a positive correlation.
Question 11.
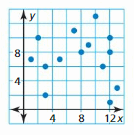
Answer:

Question 12.
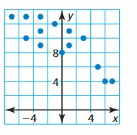
Answer:
The y-value tends to decrease as the x-value increase.
The scatter plot shows a negative correlation.
In Exercises 13 and 14, make a scatter plot of the data. Tell whether x and y show a positive, a negative, or no correlation.
Question 13.

Answer:

Question 14.

Answer:
As the x value increases, the y value decreases.
The scatter plot shows a negative correlation.
Question 15.
MODELING WITH MATHEMATICS
The table shows the world birth rates y (number of births per 1000 people) x years since 1960.
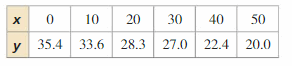
a. Write an equation that models the birthrate as a function of the number of years since 1960.
b. Interpret the slope and y-intercept of the line of fit.
Answer:
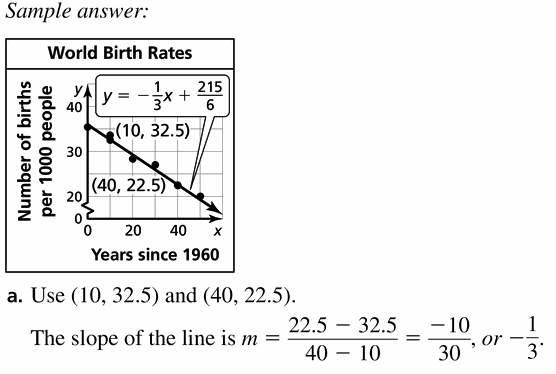
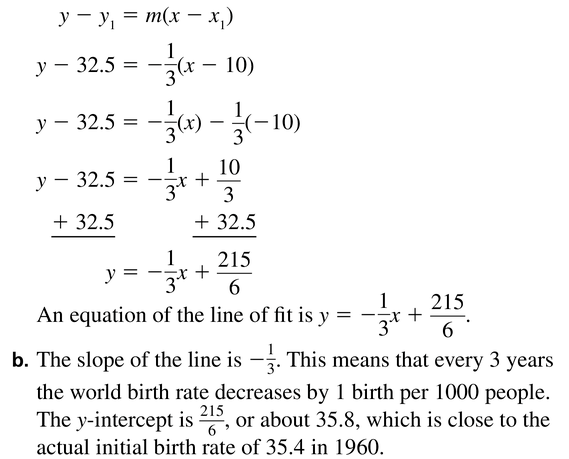
Question 16.
MODELING WITH MATHEMATICS
The table shows the total earnings y (in dollars) of a food server who works x hours.
a. Write an equation that models the server’s earnings as a function of the number of hours the server works.
b. Interpret the slope and y-intercept of the line of fit.
Answer:
a. Use the points (1, 18), (2, 40)
m = \(\frac { 40 – 18 }{ 2 – 1 } \) = 22
y – 18 = 22(x – 1)
y – 18 = 22x – 22
y = 22x – 4
b. The slope is 22 and the y-intercept is -4.
Question 17.
OPEN-ENDED
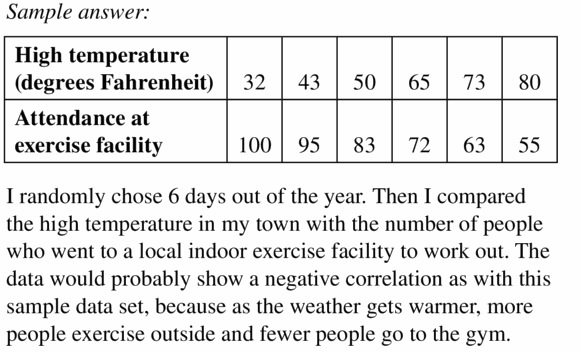
Give an example of a real-life data set that shows a negative correlation.
Answer:
Question 18.
MAKING AN ARGUMENT
Your friend says that the data in the table show a negative correlation because the dependent variable y is decreasing. Is your friend correct? Explain.
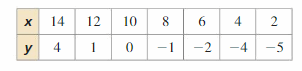
Answer:
No, because as the x value increases, the y value also increases.
The scatter plot shows a positive correlation.
Question 19.
USING TOOLS
Use a ruler or a yardstick to find the heights and arm spans of five people.
a. Make a scatter plot using the data you collected. Then draw a line of fit for the data.
b. Interpret the slope and y-intercept of the line of fit.
Answer:
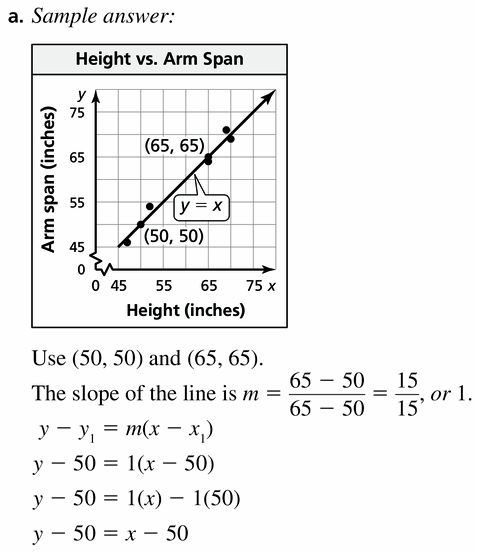

Question 20.
THOUGHT PROVOKING
A line of fit for a scatter plot is given by the equation y = 5x + 20. Describe a real-life data set that could be represented by the scatter plot.
Answer:
| x | 0 | 1 | 2 | 3 |
| y | 20 | 25 | 30 | 35 |
Substitute x = 0, y = 5(0) + 20 = 20
x = 1, y = 5(1) + 20 = 25
x = 2, y = 5(2) + 20 = 30
x = 3, y = 5(3) +20 = 35
Question 21.
WRITING
When is data best displayed in a scatter plot, rather than another type of display, such as a bar graph or circle graph?
Answer:

Question 22.
HOW DO YOU SEE IT?
The scatter plot shows part of a data set and a line of fit for the data set. Four data points are missing. Choose possible coordinates for these data points.
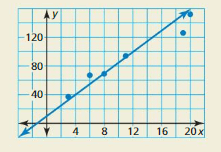
Answer:
By observing the graph the missing four data points are (10, 85), (14, 115), (16, 140), (18, 160)
Question 23.
REASONING
A data set has no correlation. Is it possible to find a line of fit for the data? Explain.
Answer:

Question 24.
ANALYZING RELATIONSHIPS
Make a scatter plot of the data in the tables. Describe the relationship between the variables. Is it possible to fit a line to the data? If so, write an equation of the line. If not, explain why.
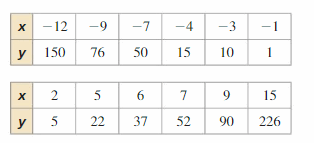
Answer:
Table 1:
\(\frac { 76 – 150 }{ -9 + 12 } \) = \(\frac { -74 }{ 3 } \)
\(\frac { 50 – 76 }{ -7 + 9 } \) = \(\frac { -26 }{ 2 } \)
Table 2:
\(\frac { 22 – 5 }{ 5 – 2 } \) = \(\frac { 17 }{ 3 } \)
\(\frac { 37 – 22 }{ 6 – 5 } \) = 15
As the slopes are different, it is not possible to fit a line to the data.
Maintaining Mathematical Proficiency
Evaluate the function when x = −3, 0, and 4. (Section 3.3)
Question 25.
g(x) = 6x
Answer:
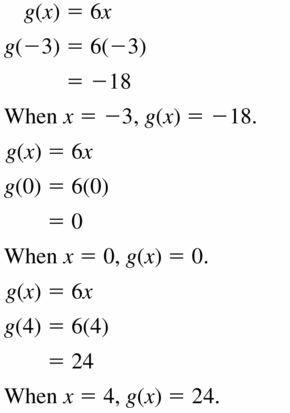
Question 26.
h(x) = -10x
Answer:
h(x) = -10x
When x = -3, h(x) = 30
h(-3) = -10(-3) = 30
When x = 0, h(x) = 0
h(0) = -10(0) = 0
When x = 4, h(x) = -40
h(4) = -10(4) = -40
Question 27.
f(x) = 5x – 8
Answer:
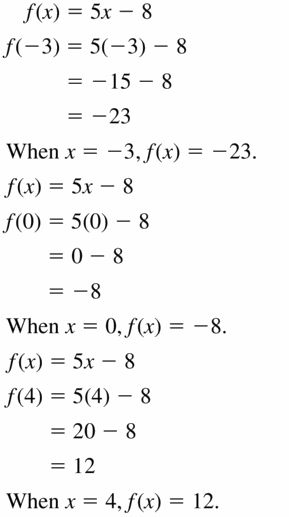
Question 28.
v(x) = 14 – 3x
Answer:
v(x) = 14 – 3x
When x = -3, v(x) = 23
v(-3) = 14 – 3(-3) = 14 + 9 = 23
When x = 0, v(x) = 14
v(0) = 14 – 3(0) = 14
When x = 4, v(x) = 2
v(4) = 14 – 3(4) = 14 – 12 = 2
Lesson 4.5 Analyzing Lines of Fit
Essential Question
How can you analytically find a line of best fit for a scatter plot?
EXPLORATION 1
Finding a Line of Best Fit
Work with a partner.
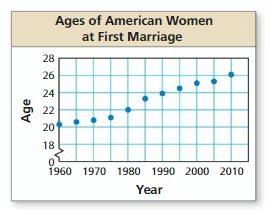
The scatter plot shows the median ages of American women at their first marriage for selected years from 1960 through 2010. In Exploration 2 in Section 4.4, you approximated a line of fit graphically. To find the line of best fit, you can use a computer, spreadsheet, or graphing calculator that has a linear regression feature.
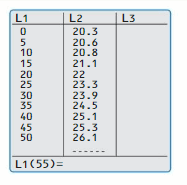
a. The data from the scatter plot is shown in the table. Note that 0, 5, 10, and so on represent the numbers of years since 1960. What does the ordered pair (25, 23.3) represent?
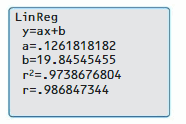
b. Use the linear regression feature to find an equation of the line of best fit. You should obtain results such as those shown below.
c. Write an equation of the line of best fit. Compare your result with the equation you obtained in Exploration 2 in Section 4.4.
Communicate Your Answer
Question 2.
How can you analytically find a line of best fit for a scatter plot?

Question 3.
The data set relates the number of chirps per second for striped ground crickets and the outside temperature in degrees Fahrenheit. Make a scatter plot of the data. Then find an equation of the line of best fit. Use your result to estimate the outside temperature when there are 19 chirps per second.
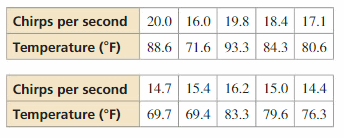
Answer:
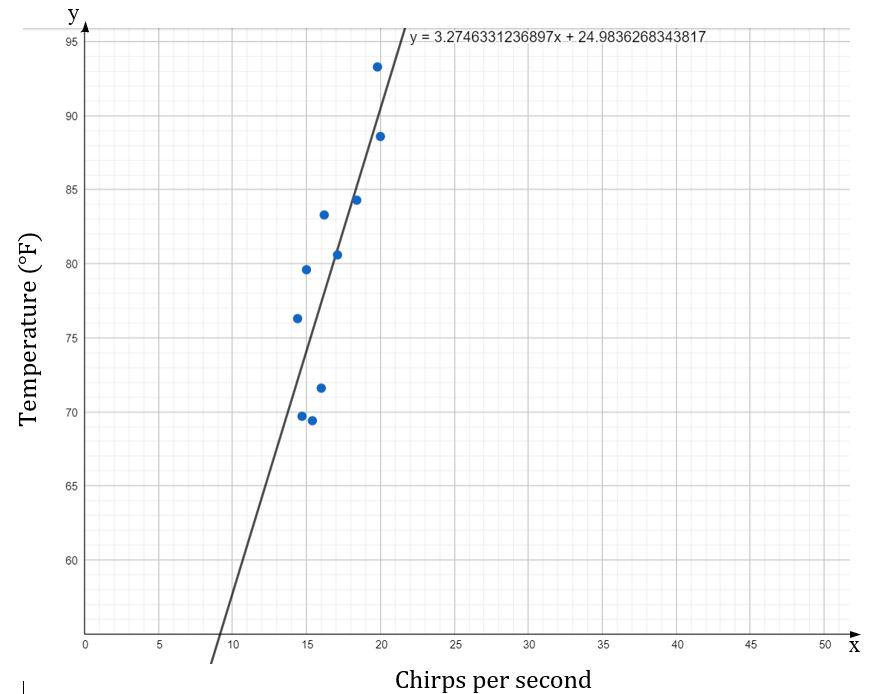
The equation of the best fit line is y = 3.275x + 24.984
x = 19 in y = 3.275x + 24.984
y = 3.275(19) + 24.984
y = 62.225 + 24.984
y = 87.209
The outside temperature is 87.2°F when there are 19 chirps per second.
4.5 Lesson
Monitoring Progress
Question 1.
The table shows the attendances y (in thousands) at an amusement park from 2005 to 2014, where x = 0 represents the year 2005. The equation y = -9.8x + 850 models the data. Is the model a good fit?

Answer:
| x | y | y value from the model | residual |
|---|---|---|---|
| 0 | 850 | 850 | 850 – 850 = 0 |
| 1 | 845 | 840.2 | 845 – 840.2 = 4.8 |
| 2 | 828 | 830.4 | 828 – 830.4 = -2.4 |
| 3 | 798 | 820.6 | 798 – 820.6 = -22.6 |
| 4 | 800 | 810.8 | 800 – 810.8 = -10.8 |
| 5 | 792 | 801 | 792 – 801 = -9 |
| 6 | 785 | 791.2 | 785 – 791.5 = -6.2 |
| 7 | 781 | 781.4 | 781 – 781.4 = -0.4 |
| 8 | 775 | 771.6 | 775 – 771.6 = 3.4 |
| 9 | 760 | 761.8 | 760 – 761.8 = -1.8 |
The points are not evenly dispersed above the horizontal axis.
y = -9.8x + 850 is not a good fit.
Question 2.
Use the data in Monitoring Progress Question 1.
(a) Use a graphing calculator to find an equation of the line of best fit. Then plot the data and graph the equation in the same viewing window.
(b) Identify and interpret the correlation coefficient.
(c) Interpret the slope and y-intercept of the line of best fit.
Answer:
a. Using the linear regression feature the equation y = -9.8x + 850 can be rounded to y = -9.6X + 844
Slope = -9.58788
y-intercept is 844.54545
r = -0.9636
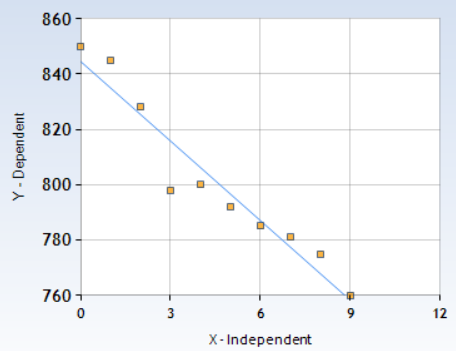
b. Correlation coefficient is -0.9636. So, the relation is a strong negative correlation.
c. Slope is -9.58788, the y-intercept is 844.54545
Question 3.
Refer to Monitoring Progress Question 2. Use the equation of the line of best fit to predict the attendance at the amusement park in 2017.
Answer:
y = -9.8x + 850
If x = 12, y = -9.8(12) + 850 = 732.4
x = 732.4
Question 4.
Is there a correlation between time spent playing video games and grade point average? If so, is there a causal relationship? Explain your reasoning.
Analyzing Lines of Fit 4.5 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
When is a residual positive? When is it negative?
Answer:

Question 2.
WRITING
Explain how you can use residuals to determine how well a line of fit models a data set.
Answer:
A residual is a measurement to determine how a to scatter plot’s data fits its trend line. The actual value is represented by the dot on the scatter plot. The predicted value is given by the trend line or line of best fit. This is the they-value that the trend line guesses our data point will appear at.
Question 3.
VOCABULARY
Compare interpolation and extrapolation.
Answer:

Question 4.
WHICH ONE DOESN’T BELONG?
Which correlation coefficient does not belong with the other three? Explain your reasoning.

Answer:
r = -0.09 does not belong with other three.
Monitoring Progress and Modeling with Mathematics
In Exercises 5–8, use residuals to determine whether the model is a good fit for the data in the table. Explain.
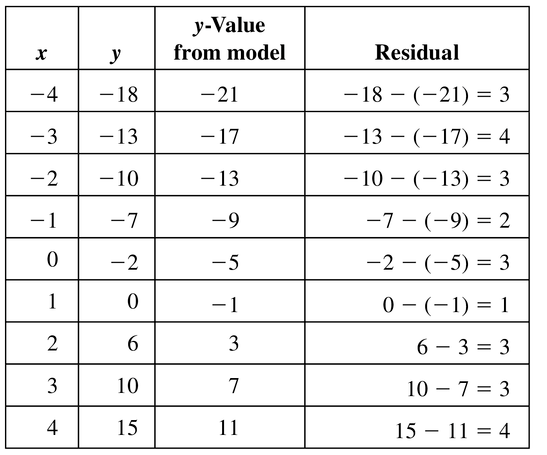
Question 5.
y = 4x – 5

Answer:
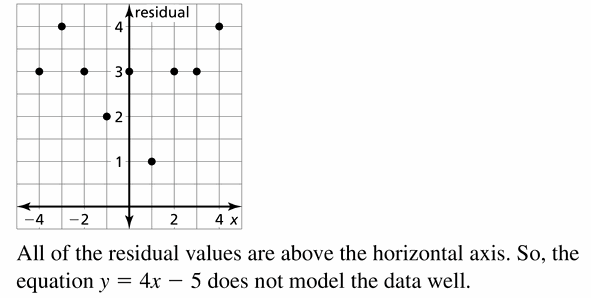
Question 6.
y = 6x + 4

Answer:
| x | y | y value from the model | residual |
|---|---|---|---|
| 1 | 13 | 10 | 13 – 10 = 3 |
| 2 | 14 | 16 | 14 – 16 = -2 |
| 3 | 23 | 22 | 23 – 22 = 1 |
| 4 | 26 | 28 | 26 – 28 = -2 |
| 5 | 31 | 34 | 31 – 34 = -3 |
| 6 | 42 | 40 | 42 – 40 = 2 |
| 7 | 45 | 46 | 45 – 46 = -1 |
| 8 | 52 | 52 | 52 – 52 = 0 |
| 9 | 62 | 58 | 62 – 58 = 4 |
The points are even;y dispersed about the horizontal axis.
The equation is a good fit.
Question 7.
y = -1.3x + 1

Answer:
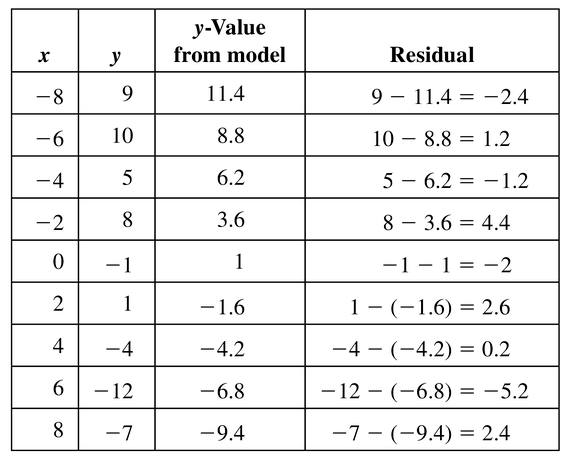
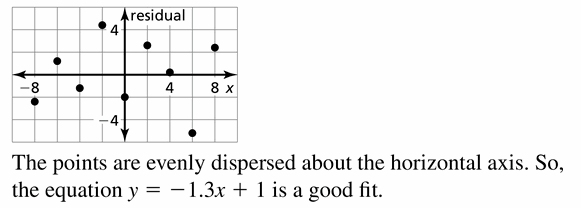
Question 8.
y = -0.5x – 2

Answer:
| x | y | y value from the model | residual |
|---|---|---|---|
| 4 | -1 | -4 | -1 + 4 = 3 |
| 6 | -3 | -5 | -3 + 5 = 2 |
| 8 | -6 | -6 | -6 + 6 = 0 |
| 10 | -8 | -7 | -8 + 7 = -1 |
| 12 | -10 | -8 | -10 + 8 = -2 |
| 14 | -10 | -9 | -10 + 9 = -1 |
| 16 | -10 | -10 | -10 + 10 = 0 |
| 18 | -9 | -11 | -9 + 11 = 2 |
| 20 | -9 | -12 | -9 + 12 = 3 |
The points are even;y dispersed about the horizontal axis.
The equation is a good fit.
Question 9.
ANALYZING RESIDUALS
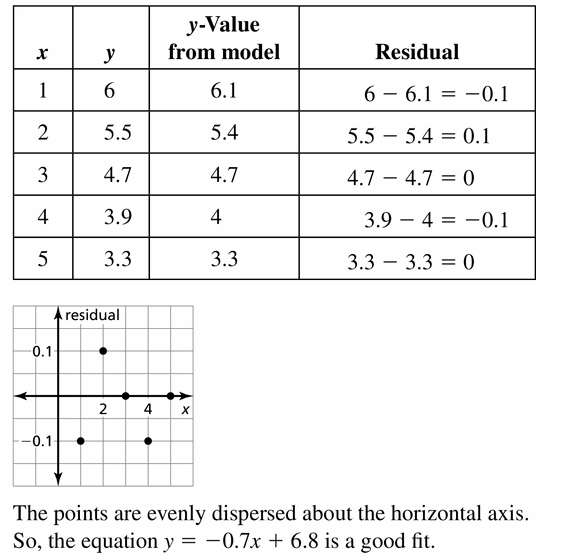
The table shows the growth y (in inches) of an elk’s antlers during week x. The equation y = -0.7x + 6.8 models the data. Is the model a good fit? Explain.

Answer:
Question 10.
ANALYZING RESIDUALS
The table shows the approximate numbers y (in thousands) of movie tickets sold from January to June for a theater. In the table, x = 1 represents January. The equation y = 1.3x + 27 models the data. Is the model a good fit? Explain.
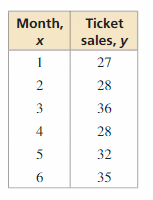
Answer:
| x | y | y value from the model | residual |
|---|---|---|---|
| 1 | 27 | 28.3 | 27 – 28.3 = -1.3 |
| 2 | 28 | 29.6 | 28 – 29.6 = -1.6 |
| 3 | 36 | 30.9 | 36 – 30.1 = 5.1 |
| 4 | 28 | 32.2 | 28 – 32.2 = -4.2 |
| 5 | 32 | 33.5 | 32 – 33.5 = -1.5 |
| 6 | 35 | 34.8 | 35 – 34.8 = 0.2 |
Most of the residuals are below the horizontal axis.
The equation does not model the data well.
In Exercises 11–14, use a graphing calculator to find an equation of the line of best fit for the data. Identify and interpret the correlation coefficient.
Question 11.

Answer:

Question 12.

Answer:
After entering the data from the table into two lists using a graphing calculator, the linear regression feature yields the equation y = -1.3x + 7.7.
The correlation coefficient is about -0.8858.
The relationship between the dependent and independent variables has a strong negative correlation and the equation closely models the data.
Question 13.
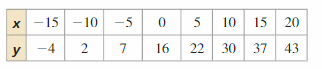
Answer:

Question 14.

Answer:
After entering the data from the table into two lists using a graphing calculator, the linear regression feature yields the equation y = -1x + 11.25.
The correlation coefficient is about -0.4435.
The relationship between the dependent and independent variables has a strong negative correlation and the equation closely models the data.
ERROR ANALYSIS
In Exercises 15 and 16, describe and correct the error in interpreting the graphing calculator display.
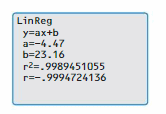
Question 15.

Answer:
Question 16.

Answer:
The data have a strong negative correlation.
Question 17.
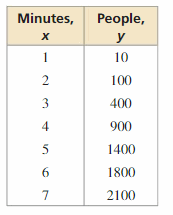
MODELING WITH MATHEMATICS
The table shows the total numbers y of people who reported an earthquake x minutes after it ended.
a. Use a graphing calculator to find an equation of the line of best fit. Then plot the data and graph the equation in the same viewing window.
b. Identify and interpret the correlation coefficient.
c. Interpret the slope and y-intercept of the line of best fit.
Answer:

Question 18.
MODELING WITH MATHEMATICS
The table shows the numbers y of people who volunteer at an animal shelter on each day x.
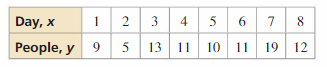
a. Use a graphing calculator to find an equation of the line of best fit. Then plot the data and graph the equation in the same viewing window.
b. Identify and interpret the correlation coefficient.
c. Interpret the slope and y-intercept of the line of best fit.
Answer:
a.
The equation is y = -2x + 19
b. correlation coefficient is 0.6193.
c. Slope is 1 and the y-intercept is 6.75.
Question 19.
MODELING WITH MATHEMATICS
The table shows the mileages x (in thousands of miles) and the selling prices y (in thousands of dollars) of several used automobiles of the same year and model.
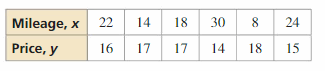
a. Use a graphing calculator to find an equation of the line of best fit.
b. Identify and interpret the correlation coefficient.

c. Interpret the slope and y-intercept of the line of best fit.
d. Approximate the mileage of an automobile that costs $15,500. e. Predict the price of an automobile with 6000 miles.
Answer:


Question 20.
MODELING WITH MATHEMATICS
The table shows the lengths x and costs y of several sailboats.
a. Use a graphing calculator to find an equation of the line of best fit.
b. Identify and interpret the correlation coefficient.
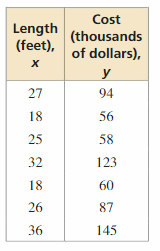
c. Interpret the slope and y-intercept of the line of best fit.
d. Approximate the cost of a sailboat that is 20 feet long.
e. Predict the length of a sailboat that costs $147,000.
Answer:
a. The line that best fit is y = 4.8x – 37.6
b. The correlation coefficient is 0.9357
c. Slope is 4.8 and y-intercept is -37.6
d. y = 4.8(20) – 37.6
y = 96 – 37.6 = 58.4
The cost of 20 feet long sailboat is 58.4 thousand dollars
e. 147 = 4.8x – 37.6
4.8x = 184.6
x = 38.45
So, the 38 ft long sailboat costs $147,000.
In Exercises 21–24, tell whether a correlation is likely in the situation. If so, tell whether there is a causal relationship. Explain your reasoning.
Question 21.
the amount of time spent talking on a cell phone and the remaining battery life
Answer:

Question 22.
the height of a toddler and the size of the toddler’s vocabulary
Answer:
Positive correlation, but there is not a casual relationship.
Question 23.
the number of hats you own and the size of your head
Answer:

Question 24.
the weight of a dog and the length of its tail
Answer:
There is no correlation between dog weight and its tail length.
Question 25.
OPEN-ENDED
Describe a data set that has a strong correlation but does not have a causal relationship.
Answer:

Question 26.
HOW DO YOU SEE IT?
Match each graph with its correlation coefficient. Explain your reasoning.
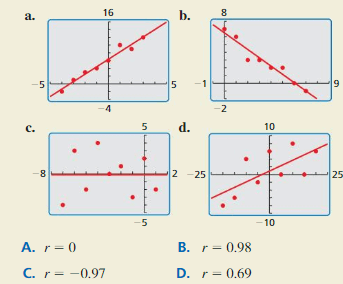
Answer:
a. The points appear to be linear and is having a positive slope.
The correlation coefficient of r = 0.98 matches the slope as it is very close to positive 1 showing a strong positive correlation.
b. The points appear to be linear and is having a negative slope.
The correlation coefficient of r = -0.97 matches the slope as it is very close to -1 showing a strong negative correlation.
c. The given graph shows scatter points. There is not a definite relationship between the two variables.
Thus there is no correlation between them and therefore the correlation coefficient is r = 0.
d. r = 0.69 as the slope in the graph is positive and somewhat linear and forms a graph of positive correlation as given in the question.
Question 27.
ANALYZING RELATIONSHIPS
The table shows the grade point averages y of several students and the numbers x of hours they spend watching television each week.
a. Use a graphing calculator to find an equation of the line of best fit. Identify and interpret the correlation coefficient.
b. Interpret the slope and y-intercept of the line of best fit.
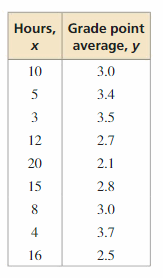
c. Another student watches about 14 hours of television each week. Approximate the student’s grade point average.
d. Do you think there is a causal relationship between time spent watching television and grade point average? Explain.
Answer:


Question 28.
MAKING AN ARGUMENT
A student spends 2 hours watching television each week and has a grade point average of 2.4. Your friend says including this information in the data set in Exercise 27 will weaken the correlation. Is your friend correct? Explain.
Answer:
No, the correlation is -0.6672. It is a moderate negative correlation.
Question 29.
USING MODELS
Refer to Exercise 17.
a. Predict the total numbers of people who reported an earthquake 9 minutes and 15 minutes after it ended.
b. The table shows the actual data. Describe the accuracy of your extrapolations in part (a).
Answer:

Question 30.
THOUGHT PROVOKING
A data set consists of the numbers x of people at Beach 1 and the numbers y of people at Beach 2 recorded daily for 1 week. Sketch a possible graph of the data set. Describe the situation shown in the graph and give a possible correlation coefficient. Determine whether there is a causal relationship. Explain.
Answer:
| Day | People at Beach 1 | People at Beach 2 |
|---|---|---|
| 1 | 16 | 15 |
| 2 | 21 | 18 |
| 3 | 25 | 30 |
| 4 | 36 | 41 |
| 5 | 47 | 39 |
| 6 | 83 | 71 |
| 7 | 79 | 90 |
These data were plotted on a coordinate axis system. A line was also graphed that fits the data function resulting
y = 0.97x + 099
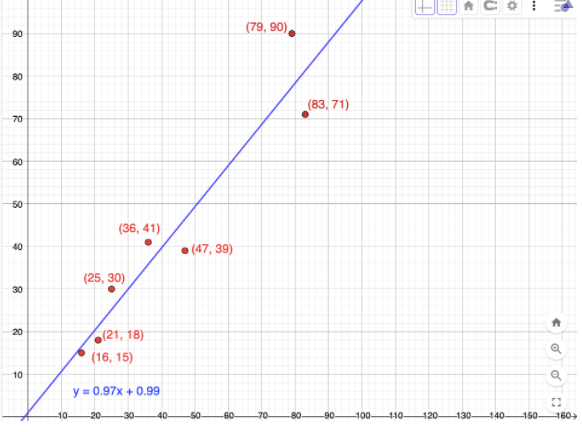
Question 31.
COMPARING METHODS
The table shows the numbers y (in billions) of text messages sent each year in a five-year period, where x = 1 represents the first year in the five-year period.
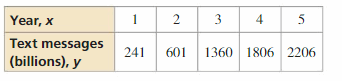
a. Use a graphing calculator to find an equation of the line of best fit. Identify and interpret the correlation coefficient.
b. Is there a causal relationship? Explain your reasoning.
c. Calculate the residuals. Then make a scatter plot of the residuals and interpret the results.
d. Compare the methods you used in parts (a) and (c) to determine whether the model is a good fit. Which method do you prefer? Explain.
Answer:

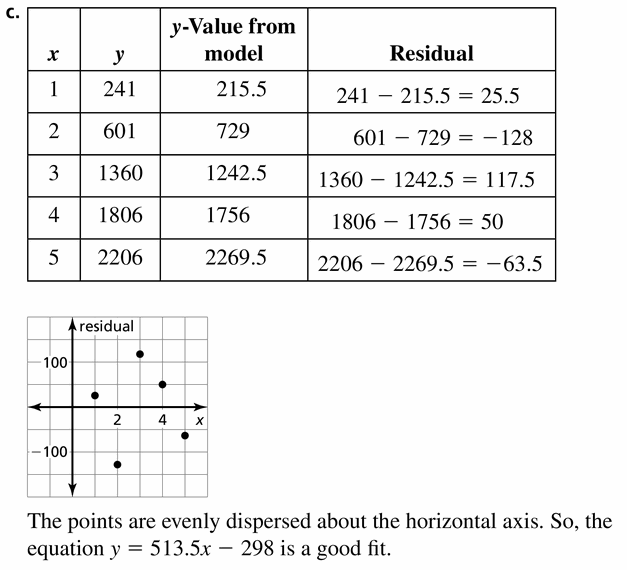

Maintaining Mathematical Proficiency
Determine whether the table represents a linear or nonlinear function. Explain. (Section 3.2)
Question 32.

Answer:
Nonlinear function
Question 33.

Answer:

Lesson 4.6 Arithmetic Sequences
Essential Question
How can you use an arithmetic sequence to describe a pattern?
Answer:
An arithmetic sequence is a list of numbers with a definite pattern. If you take any number in the sequence and then subtract it from the previous one, and the result is always the same or constant then it is an arithmetic sequence.
EXPLORATION 1
Describing a Pattern
Work with a partner. Use the figures to complete the table. Plot the points given by your completed table. Describe the pattern of the y-values.
Communicate Your Answer
Question 2.
How can you use an arithmetic sequence to describe a pattern? Give an example from real life.
Answer:
An arithmetic sequence is a list of numbers with a definite pattern. If you take any number in the sequence and then subtract it from the previous one, and the result is always the same or constant then it is an arithmetic sequence.
Question 3.
In chemistry, water is called H2O because each molecule of water has two hydrogen atoms and one oxygen atom. Describe the pattern shown below. Use the pattern to determine the number of atoms in 23 molecules.
4.6 Lesson
Monitoring Progress
Write the next three terms of the arithmetic sequence.
Question 1.
-12, 0, 12, 24, . . .
Answer:
| Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Term | -12 | 0 | 12 | 24 | 36 | 48 | 60 |
Add -12 to the term to find the next term.
The next 3 terms are 36, 48, 60.
Question 2.
0.2, 0.6, 1, 1.4, . . .
Answer:
| Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Term | 0.2 | 0.6 | 1 | 1.4 | 1.8 | 2.2 | 2.6 |
Add 0.4 to the term to get the next term.
The next 3 terms are 1.8, 2.2, 2.6
Question 3.
4, 3\(\frac{3}{4}\), 3\(\frac{1}{2}\), 3\(\frac{1}{4}\)
Answer:
Subtract 0.25 from each term to find next term
| Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Term | 4 | 3(3/4) | 3(1/2) | 3(1/4) | 3 | 2(3/4) | 2(1/2) |
The next 3 terms are 3, 2(3/4), 2(1/2)
Graph the arithmetic sequence. What do you notice?
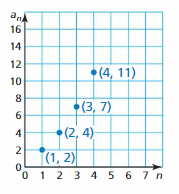
Question 4.
3, 6, 9, 12, . . .
Answer:
| Position | 1 | 2 | 3 | 4 |
| Term | 3 | 6 | 9 | 12 |
Thus, the points lie on the same line.
Question 5.
4, 2, 0, -2, . . .
Answer:
| Position | 1 | 2 | 3 | 4 |
| Term | 4 | 2 | 0 | -2 |
The points lie on the same line
Question 6.
1, 0.8, 0.6, 0.4, . . .
Answer:
| Position | 1 | 2 | 3 | 4 |
| Term | 1 | 0.8 | 0.6 | 0.4 |
The points lie on the same line.
Question 7.
Does the graph shown represent an arithmetic sequence? Explain.
Answer:
Yes
Write an equation for the nth term of the arithmetic sequence. Then find a25.
Question 8.
4, 5, 6, 7, . . .
Answer:
The nth term is an = a1 + (n – 1)d
an = 4 + (n – 1)1 = 4 + n – 1 = 3 + n
a25 = 3 + 25 = 28
The equation for nth term is an = 3 + n, a25 = 28
Question 9.
8, 16, 24, 32, . . .
Answer:
The nth term is an = a1 + (n – 1)d
an = 8 + (n – 1)8 = 8 + 8n – 8 = 8n
a25 = 8(25) = 200
The equation for nth term is an = 8n, a25 = 200
Question 10.
1, 0, -1, -2, . . .
Answer:
The nth term is an = a1 + (n – 1)d
an = 1 + (n – 1)1 = 1 + n – 1 = n
a25 = 25
The equation for nth term is an = n, a25 = 25
Question 11.
A carnival charges $2 for each game after you pay a $5 entry fee.
a. Write a function that represents the arithmetic sequence.
b. Graph the function.
c. How many games can you play when you take $29 to the carnival?
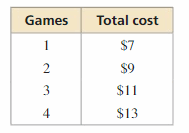
Answer:
a. f(n) = a1 + (n – 1)d
f(n) = 7 + (n – 1)2
= 7 + 2n – 2 = 2n + 5
The function f(n) = 2n + 5 represents the arithmetic sequence.
c. 29 = 2n + 5
24 = 2n
n = 12
b. 
c. You can play 12 games when you take $29 to the carnival.
Arithmetic Sequences 4.6 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
Describe the graph of an arithmetic sequence.
Answer:
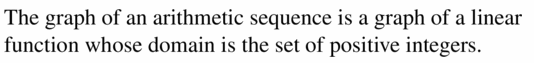
Question 2.
DIFFERENT WORDS, SAME QUESTION
Consider the arithmetic sequence represented by the graph. Which is different? Find “both” answers.

Answer:
Find the difference between the terms a2 and a4.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 and 4, write the next three terms of the arithmetic sequence.
Question 3.
First term: 2
Common difference: 13
Answer:
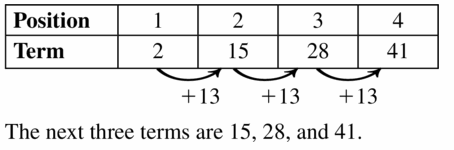
Question 4.
First term: 18
Common difference: −6
Answer:
| Position | 1 | 2 | 3 | 4 |
| Term | 18 | 12 | 6 | 0 |
First term: 18
Common difference: −6
18 – 6 = 12
12 – 6 = 6
6 – 0 = 6
The next 3 terms are 12, 6, 0.
In Exercises 5−10, find the common difference of the arithmetic sequence.
Question 5.
13, 18, 23, 28, . . .
Answer:
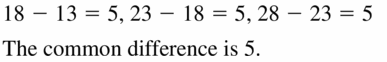
Question 6.
175, 150, 125, 100, . . .
Answer:
Given sequence is 175, 150, 125, 100, . . .
a1 = 175
150 – 175 = -25, 125 – 150 = -25, 100 – 125 = -25
The common difference is -25.
Question 7.
-16, -12, -8, -4, . . .
Answer:
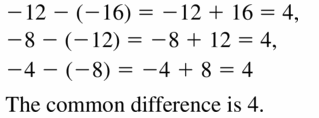
Question 8.
4, 3\(\frac{2}{3}\), 3\(\frac{1}{3}\), 3, . . .
Answer:
Given sequence,
4, 3\(\frac{2}{3}\), 3\(\frac{1}{3}\), 3, . . .
a1 = 4
3\(\frac{2}{3}\) – 4 = \(\frac{-1}{3}\), 3\(\frac{1}{3}\) – 3\(\frac{2}{3}\) = \(\frac{-1}{3}\), 3 – 3\(\frac{1}{3}\) = \(\frac{-1}{3}\)
The common difference is \(\frac{-1}{3}\)
Question 9.
6.5, 5, 3.5, 2, . . .
Answer:
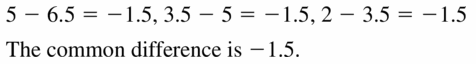
Question 10.
-16, -7, 2, 11, . . .
Answer:
Given sequence is -16, -7, 2, 11, . . .
-7 + 16 = 9
2 + 7 = 9
11 – 2 = 9
The common difference is 9
In Exercises 11−16, write the next three terms of the arithmetic sequence.
Question 11.
19, 22, 25, 28, . . .
Answer:
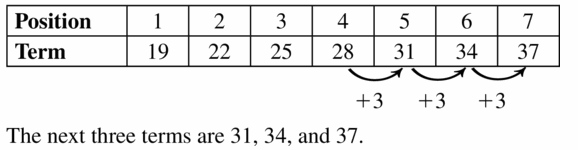
Question 12.
1, 12, 23, 34, . . .
Answer:
| Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Term | 1 | 12 | 23 | 34 | 46 | 58 | 70 |
The next 3 terms are 46, 58, 70
Question 13.
16, 21, 26, 31, . . .
Answer:
Question 14.
60, 30, 0, -30, . . .
Answer:
| Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Term | 60 | 30 | 0 | -30 | -60 | -90 | -120 |
The next 3 terms are -60, -90, -120.
Question 15.
1.3, 1, 0.7, 0.4, . . .
Answer:

Question 16.
\(\frac{5}{6}\), \(\frac{2}{3}\), \(\frac{1}{2}\), \(\frac{1}{3}\), . . .
Answer:
Given sequence is \(\frac{5}{6}\), \(\frac{2}{3}\), \(\frac{1}{2}\), \(\frac{1}{3}\), . . .
| Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Term | \(\frac{5}{6}\) | \(\frac{2}{3}\) | \(\frac{1}{2}\) | \(\frac{1}{3}\) | \(\frac{1}{6}\) | 0 | \(\frac{-1}{6}\) |
The next 3 terms are \(\frac{1}{6}\), 0, \(\frac{-1}{6}\)
In Exercises 17−22, graph the arithmetic sequence.
Question 17.
4, 12, 20, 28, . . .
Answer:
Question 18.
-15, 0, 15, 30, . . .
Answer:
Given sequence is -15, 0, 15, 30, . . .
a1 = -15
| Position | 1 | 2 | 3 | 4 |
| Term | -15 | 0 | 15 | 30 |
Question 19.
−1, −3, −5, −7, . . .
Answer:
Question 20.
2, 19, 36, 53, . . .
Answer:
Given sequence is 2, 19, 36, 53, . . .
| Position | 1 | 2 | 3 | 4 |
| Term | 2 | 19 | 36 | 53 |
Question 21.
0, 41\(\frac{1}{2}\), 9, 13\(\frac{1}{2}\), . . .
Answer:
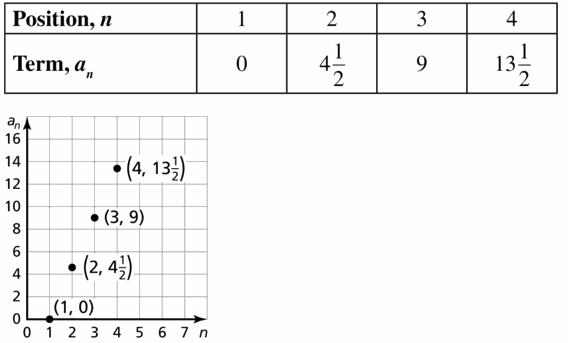
Question 22.
6, 5.25, 4.5, 3.75, . . .
Answer:
Given sequence is 6, 5.25, 4.5, 3.75, . . .
a1 = 6
| Position | 1 | 2 | 3 | 4 |
| Term | 6 | 5.25 | 4.5 | 3.75 |
In Exercises 23−26, determine whether the graph represents an arithmetic sequence. Explain.
Question 23.
Answer:
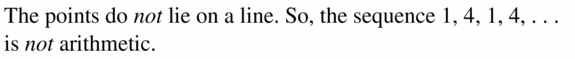
Question 24.
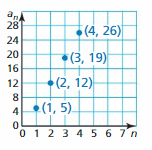
Answer:
| Position | 1 | 2 | 3 | 4 |
| Term | 5 | 12 | 19 | 26 |
The consecutive terms have a common difference of 7.
So, graph 5, 12, 19, 26 represents the arithmetic sequence.
Question 25.
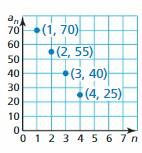
Answer:

Question 26.
Answer:
| Position | 1 | 2 | 3 | 4 |
| Term | 2 | 10 | 16 | 20 |
The consecutive terms do not have a common difference
The points lie on the line.
So, graph 2, 10, 16, 20, . . represents the arithmetic sequence.
In Exercises 27−30, determine whether the sequence is arithmetic. If so, find the common difference.
Question 27.
13, 26, 39, 52, . . .
Answer:
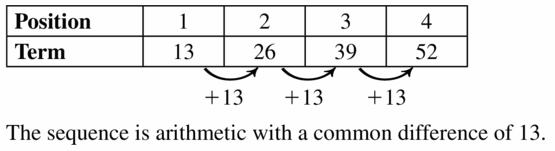
Question 28.
5, 9, 14, 20, . . .29.
Answer:
| Position | 1 | 2 | 3 | 4 |
| Term | 5 | 9 | 14 | 20 |
There is no common difference.
The sequence is not arithmetic.
Question 29.
48, 24, 12, 6, . . .
Answer:

Question 30.
87, 81, 75, 69, . . .
Answer:
| Position | 1 | 2 | 3 | 4 |
| Term | 87 | 81 | 75 | 69 |
The sequence is arithmetic with a common difference of 6.
It represents an arithmetic sequence.
Question 31.
FINDING A PATTERN
Write a sequence that represents the number of smiley faces in each group. Is the sequence arithmetic? Explain.

Answer:
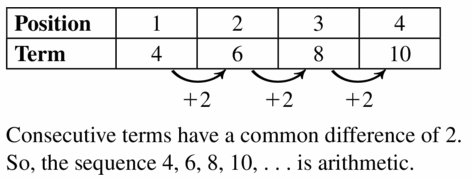
Question 32.
FINDING A PATTERN
Write a sequence that represents the sum of the numbers in each roll. Is the sequence arithmetic? Explain.
Answer:
| Position | 1 | 2 | 3 | 4 |
| Term | 2 | 5 | 9 | 11 |
There is no common difference.
So, the sequence is not arithmetic.
In Exercises 33−38, write an equation for the nth term of the arithmetic sequence. Then find a10.
Question 33.
-5, -4, -3, -2, . . .
Answer:

Question 34.
-6, -9, -12, -15, . . .
Answer:
Given,
-6, -9, -12, -15, . . .
d = -9 -(-6) = -9 + 6 = -3
an = a₁ + (n – 1)d
= -6 + (n – 1)(-3)
= -6 – 3n + 3
= -3 – 3n
An equation for the nth term of the arithmetic sequence is an = -3 – 3n
a10 = -3 – 3(10) = -3 – 30
= -33
a10 = -33
Question 35.
\(\frac{1}{2}\), 1, 1\(\frac{1}{2}\), 2, ……
Answer:

Question 36.
100, 110, 120, 130, ….
Answer:
Given,
100, 110, 120, 130, ….
d = 110 – 100 = 10
an = a₁ + (n – 1)d
= 100 + (n – 1)(10)
= 100 + 10n – 10
= 10n + 90
An equation for the nth term of the arithmetic sequence is an = 10n + 90
a10 = 10(10) + 90 = 100 + 90
= 190
a10 = 190
Question 37.
10, 0, -10, -20, ……
Answer:

Question 38.
\(\frac{3}{7}\), \(\frac{4}{7}\), \(\frac{5}{7}\), \(\frac{6}{7}\), ………
Answer:
Given,
\(\frac{3}{7}\), \(\frac{4}{7}\), \(\frac{5}{7}\), \(\frac{6}{7}\), ………
d = \(\frac{4}{7}\) – \(\frac{3}{7}\) = \(\frac{1}{7}\)
an = a₁ + (n – 1)d
= \(\frac{3}{7}\) + (n – 1)(\(\frac{1}{7}\))
= \(\frac{3}{7}\) + \(\frac{n}{7}\) – \(\frac{3}{7}\)
= \(\frac{2 + n}{7}\)
An equation for the nth term of the arithmetic sequence is an = \(\frac{2 + n}{7}\)
a10 = \(\frac{2 + 10}{7}\)
= \(\frac{12}{7}\)
Question 39.
ERROR ANALYSIS
Describe and correct the error in finding the common difference of the arithmetic sequence.
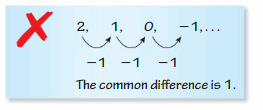
Answer:
Question 40.
ERROR ANALYSIS
Describe and correct the error in writing an equation for the nth term of the arithmetic sequence.

Answer:
The nth term in the sequence is an = a₁ + (n – 1)d
an = 14 + (n – 1)8
Question 41.
NUMBER SENSE
The first term of an arithmetic sequence is 3. The common difference of the sequence is 1.5 times the first term. Write the next three terms of the sequence. Then graph the sequence.
Answer:

Question 42.
NUMBER SENSE
The first row of a dominoes display has 10 dominoes. Each row after the first has two more dominoes than the row before it. Write the first five terms of the sequence that represents the number of dominoes in each row. Then graph the sequence.

Answer:
Given,
The first row of a dominoes display has 10 dominoes. Each row after the first has two more dominoes than the row before it.
The equation to give the number of dominoes in the nth row is an = a₁ + (n – 1)d
= 10 + (n – 1)2
= 10 + 2n – 2
= 2n + 8
The nth term of the arithmetic sequence is an = 2n + 8
First row a1 = 10
second row a2 = 2(2) + 8 = 12
third row a3 = 2(3) + 8 = 14
fourth row = 2(4) + 8 = 16
fifth row = 2(5) + 8 = 18
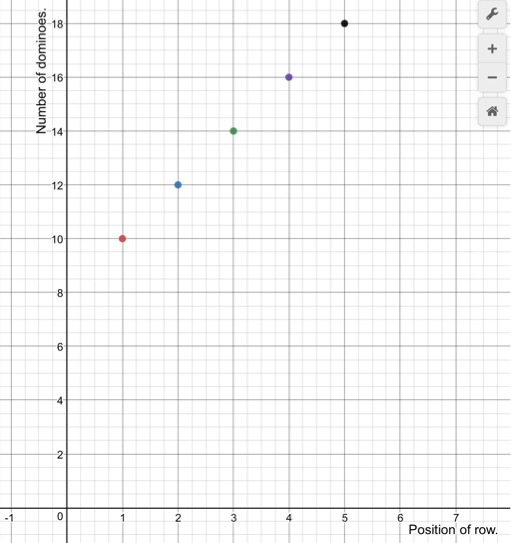
REPEATED REASONING
In Exercises 43 and 44, (a) draw the next three figures in the sequence and (b) describe the 20th figure in the sequence.
Question 43.

Answer:
Question 44.
Answer:
a. The next three figures are
Question 45.
MODELING WITH MATHEMATICS
The total number of babies born in a country each minute after midnight January 1st can be estimated by the sequence shown in the table. (See Example 5.)
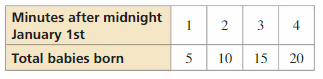
a. Write a function that represents the arithmetic sequence.
b. Graph the function.
c. Estimate how many minutes after midnight January 1st it takes for 100 babies to be born.
Answer:


Question 46.
MODELING WITH MATHEMATICS
The amount of money a movie earns each week after its release can be approximated by the sequence shown in the graph.
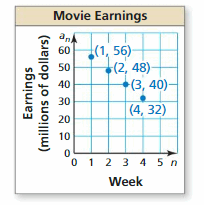
a. Write a function that represents the arithmetic sequence.
b. In what week does the movie earn $16 million?
c. How much money does the movie earn overall?
Answer:
a. Common difference is d = 48 – 56 = -8
Arithmetic sequence of nth term = 56 + (n – 1)(-8)
= 56 – 8n + 8 = 64 – 8n
b. 16 = 64 – 8n
8n = 64 – 16
8n = 48
n = 6
c. 0 = 64 – 8n
64 = 8n
n = 8
The sum of amount earned in 8 weeks = 56 + 48 + 40 + 32 + 24 + 16 + 8
= 224
MATHEMATICAL CONNECTIONS
In Exercises 47 and 48, each small square represents 1 square inch. Determine whether the areas of the figures form an arithmetic sequence. If so, write a function f that represents the arithmetic sequence and find f(30).
Question 47.
Answer:

Question 48.
Answer:
| Position | 1 | 2 | 3 |
| Term | 4 | 6 | 25 |
The above boxes do not represent the arithmetic sequence.
Question 49.
REASONING
Is the domain of an arithmetic sequence discrete or continuous? Is the range of an arithmetic sequence discrete or continuous?
Answer:

Question 50.
MAKING AN ARGUMENT
Your friend says that the range of a function that represents an arithmetic sequence always contains only positive numbers or only negative numbers. Your friend claims this is true because the domain is the set of positive integers and the output values either constantly increase or constantly decrease. Is your friend correct? Explain.
Answer:
The friend is not correct.
The range of the arithmetic sequence contains positive, negative and both.
For example, let the first term of the sequence is 5, the common difference is -2
The terms will be 5, 3, 1, -1,…
Question 51.
OPEN-ENDED
Write the first four terms of two different arithmetic sequences with a common difference of -3. Write an equation for the nth term of each sequence.
Answer:

Question 52.
THOUGHT PROVOKING
Describe an arithmetic sequence that models the numbers of people in a real-life situation.
Answer:
Question 53.
REPEATED REASONING
Firewood is stacked in a pile. The bottom row has 20 logs, and the top row has 14 logs. Each row has one more log than the row above it. How many logs are in the pile?
Answer:
Question 54.
HOW DO YOU SEE IT?
The bar graph shows the costs of advertising in a magazine.
a. Does the graph represent an arithmetic sequence? Explain.
b. Explain how you would estimate the cost of a six-page advertisement in the magazine.
Answer:
a. The graph does not represent the arithmetic sequence as they do not have a common difference.
Question 55.
REASONING
Write a function f that represents the arithmetic sequence shown in the mapping diagram.
Answer:

Question 56.
PROBLEM SOLVING
A train stops at a station every 12 minutes starting at 6:00 A.M. You arrive at the station at 7:29 A.M. How long must you wait for the train?
Answer:
A train stops at a station every 12 minutes starting at 6:00 A.M
Therefore, the sequence is 6:12, 6:24, 6:36, 6:48, 7:00, 7:12, 7:24, . . .
You arrive at the station at 7:29 AM
The train will stop at 7:36 AM
36 – 29 = 7 minutes
Question 57.
ABSTRACT REASONING
Let x be a constant. Determine whether each sequence is an arithmetic sequence. Explain.
a. x + 6, 3x + 6, 5x + 6, 7x + 6, . . .
b. x + 1, 3x + 1, 9x + 1, 27x + 1, . . .
Answer:
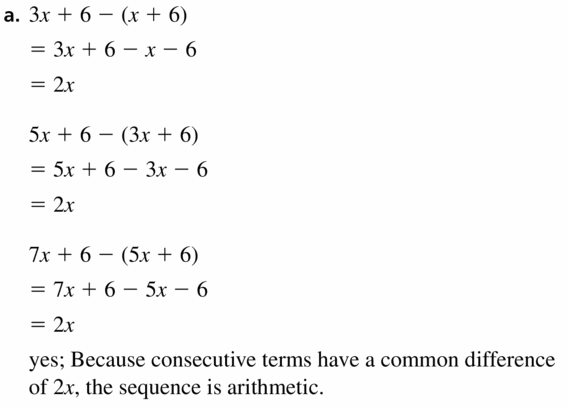
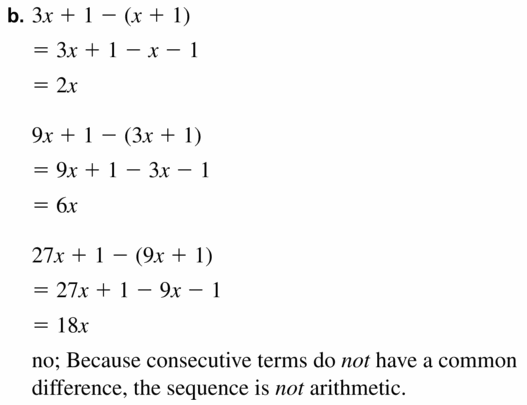
Maintaining Mathematical ProficiencySolve the inequality. Graph the solution. (Section 2.2)
Question 58.
x + 8 ≥ -9
Answer:
Given,
x + 8 ≥ -9
x ≥ -9 – 8
x ≥ -17
Question 59.
15 < b – 4
Answer:
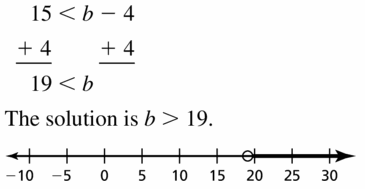
Question 60.
t – 21 < -12
Answer:
Given,
t – 21 < -12
t < -12 + 21
t < 9

Question 61.
7 + y ≤ 3
Answer:
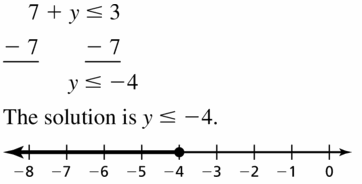
Graph the function. Compare the graph to the graph of f(x) = | x |. Describe the domain and range. (Section 3.7)
Question 62.
h(x) = 3 | x |
Answer:
| x | 1 | 2 | 3 | 4 |
| h(x) | 3 | 6 | 9 | 12 |
Question 63.
v(x) = | x – 5 |
Answer:

Question 64.
g(x) = | x | + 1
Answer:
Question 65.
r(x) = -2 | x |
Answer:
Lesson 4.7 Piecewise Functions
Essential Question
How can you describe a function that is represented by more than on equation?
EXPLORATION 1
Writing Equations for a Function
Work with a partner.
a. Does the graph represent y as a function of x? Justify your conclusion.
b. What is the value of the function when x = 0? How can you tell?
c. Write an equation that represents the values of the function when x ≤ 0.
![]()
d. Write an equation that represents the values of the function when x > 0.
![]()
e. Combine the results of parts (c) and (d) to write a single description of the function.

EXPLORATION 2
Writing Equations for a Function
Work with a partner.
a. Does the graph represent y as a function of x? Justify your conclusion.
b. Describe the values of the function for the following intervals.
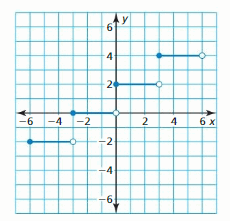
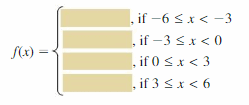
Communicate Your Answer
Question 3.
How can you describe a function that is represented by more than one equation?
Question 4.
Use two equations to describe the function represented by the graph.
4.7 LessonMonitoring Progress
Evaluate the function.
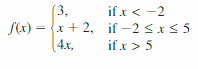
Question 1.
f(-8)
Answer:
f(-8) = 3 because x < -2
Question 2.
f(-2)
Answer:
f(x) = x + 2
x = -2
f(-2) = -2 + 2
f(-2) = 0
Question 3.
f(0)
Answer:
f(x) = x + 2
x = 0
f(0) = 0 + 2
f(0) = 2
Question 4.
f(3)
Answer:
f(x) = x + 2
x = 3
f(3) = 3 + 2
f(3) = 5
Question 5.
f(5)
Answer:
f(x) = x + 2
x = 5
f(5) = 5 + 2 = 7
Question 6.
f(10)
Answer:
f(x) = 4x
x = 10
f(10) = 4(10) = 40 as x > 5
Describe the domain and range.
Question 7.
![]()
Answer:
The first line points downwards in the third quadrant.
The second line is in the fourth quadrant.
The range is -1.
The domain is 1.
Question 8.
![]()
Answer:
Write a piecewise function for the graph.
Question 9.
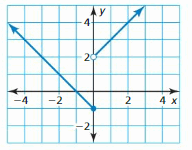
Answer:
When x > 0, the line is y = x + 2
When x ≤ 0, the line is y = x – 1
Question 10.
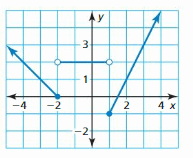
Answer:
The straight-line equation is y = 2, when -2 ≤ x ≤ 1
The left side equation is y = -2 + x when x < 0
The right side equation is y = -x when x > 0
Question 11.
A landscaper rents a wood chipper for 4 days. The rental company charges $100 for the first day and $50 for each additional day. Write and graph a step function that represents the relationship between the number x of days and the total cost y (in dollars) of renting the chipper.
Answer:
Given,
A landscaper rents a wood chipper for 4 days.
The rental company charges $100 for the first day and $50 for each additional day.
The total cost, y is given by
y = 100 + 50x where x is the number of days
When graphing, using y=mx+c,
the gradient will be always 50 and at point when x = 0, y = 100 when x = 1, y = 150, when x = 2, y = 200 when x = 3, y = 250 and when x = 4, y = 300
Question 12.
WHAT IF?
The reference beam originates at (3, 0) and reflects off a mirror at (5, 4).
a. Write an absolute value function that represents the path of the reference beam.
b. Write the function in part (a) as a piecewise function.
Answer:
Given,
The reference beam originates at (3, 0) and reflects off a mirror at (5, 4).
The vertex of the path of the reference beam is (3, 0). So, the function has the form g(x) = a|x – 3|.
Substitute the coordinates (5, 4)
4 = a|4 – 3|
4 = a
So, the function g(x) = 4|x – 3| represents the path of the reference beam
Piecewise Functions 4.7 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
Compare piecewise functions and step functions.
Answer:

Question 2.
WRITING
Use a graph to explain why you can write the absolute value function y = | x | as a piecewise function.
Answer:
Monitoring Progress and Modeling with MathematicsIn Exercises 3–12, evaluate the function.
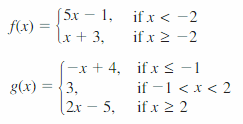
Question 3.
f(-3)
Answer:
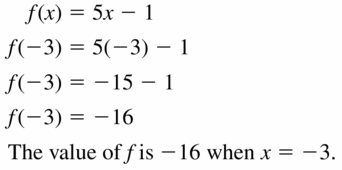
Question 4.
f(-2)
Answer:
f(x) = x + 3
x = -2
f(-2) = -2 + 3 = 1
Question 5.
f(0)
Answer:
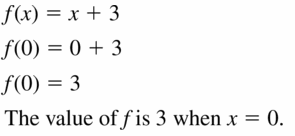
Question 6.
f(5)
Answer:
f(x) = x + 3
x = 5
f(5) = 5 + 3 = 8
Question 7.
g(-4)
Answer:
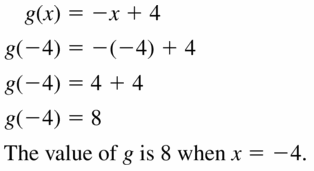
Question 8.
g(-1)
Answer:
g(x) = -x + 4
x = -1
(g(-1) = -(-1) + 4 = 5
Question 9.
g(0)
Answer:
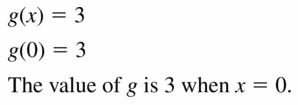
Question 10.
g(1)
Answer:
g(x) = 3
x = 1
g(1) = 3
Question 11.
g(2)
Answer:
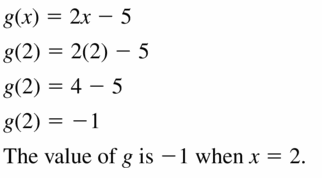
Question 12.
g(5)
Answer:
g(x) = 2x – 5
x = 5
g(5) = 2(5) – 5 = 10 – 5 = 5
Question 13.
MODELING WITH MATHEMATICS
On a trip, the total distance (in miles) you travel in x hours is represented by the piecewise function
![]()
How far do you travel in 4 hours?
Answer:
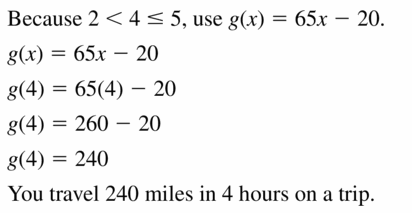
Question 14.
MODELING WITH MATHEMATICS
The total cost (in dollars) of ordering x custom shirts is represented by the piecewise function
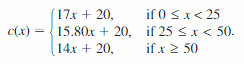
Determine the total cost of ordering 26 shirts.

Answer:
c(x) = 15.80x + 20
c(26) = 15.80(26) + 20
= 430.8
The total cost of ordering 26 shirts is $430.8
In Exercises 15–20, graph the function. Describe the domain and range.
Question 15.
![]()
Answer:
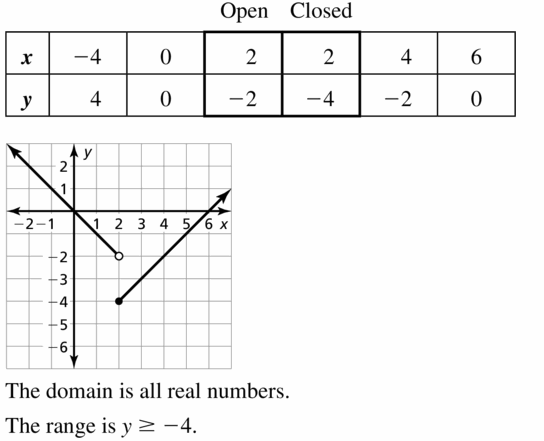
Question 16.
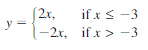
Answer:
| x | -6 | -3 | -3 | 6 |
| y | -18 | -9 | 9 | 18 |
The domain is all real numbers and the range is y ≤ -3.
Question 17.
![]()
Answer:
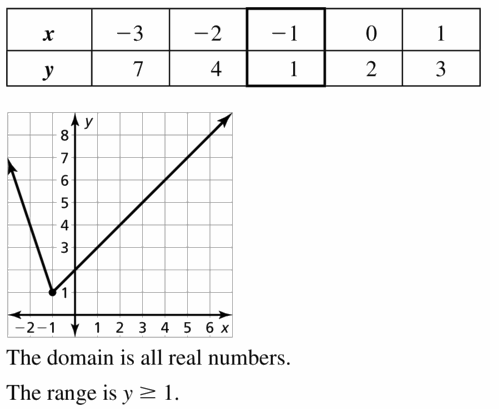
Question 18.
![]()
Answer:
| x | 0 | 2 | 4 | 4 |
| y | 8 | 10 | 14 | 12 |
The domain is all real numbers and the range is y < 4
Question 19.
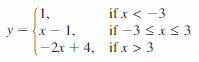
Answer:
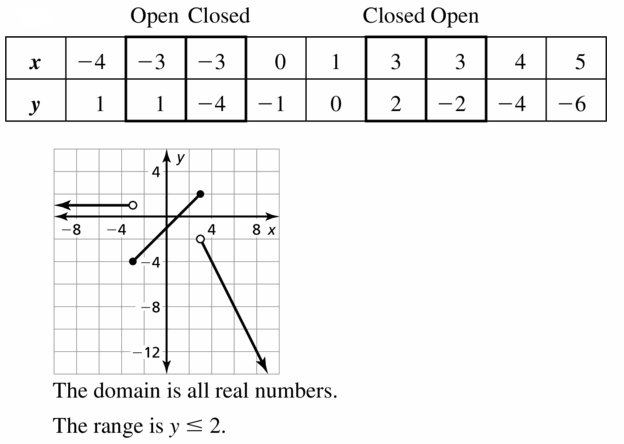
Question 20.
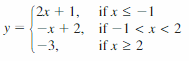
Answer:
| x | -1 | 0 | 1 | 2 | 2 |
| y | -1 | 2 | 1 | 0 | -3 |
The domain is all real numbers and the range is y < 2.
Question 21.
ERROR ANALYSIS
Describe and correct the error in finding f(5) when ![]()
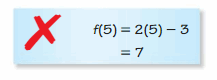
Answer:
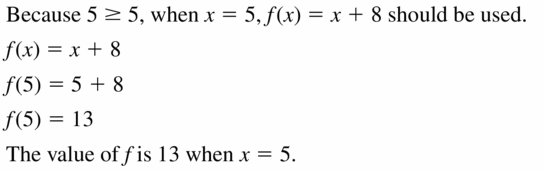
Question 22.
ERROR ANALYSIS
Describe and correct the error in graphing ![]()
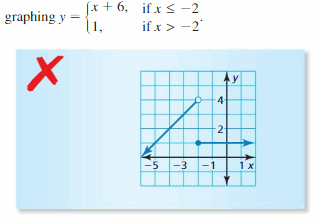
Answer:
The graph is wrong for the first statement.
In Exercises 23–30, write a piecewise function for the graph.
Question 23.
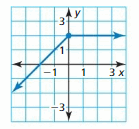
Answer:

Question 24.
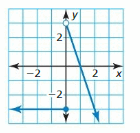
Answer:
For x ≤ 0, y = -3
use the points (0, 3) and (1, 1)
m = \(\frac { 1 – 3 }{ 1 – 0 } \) = -2
slope = y – y1 = m(x – x1)
y – 1 = -2(x – 1)
y – 1 = -2x + 2
y = -2x + 3, for x < 0
Question 25.
Answer:
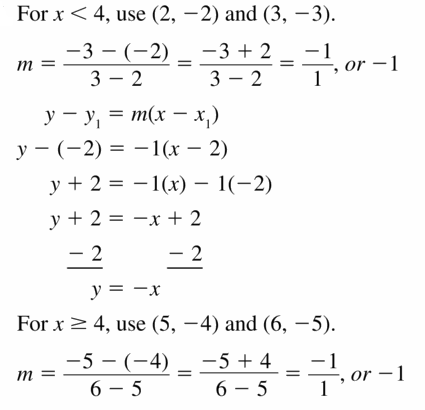
Question 26.
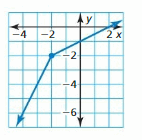
Answer:
The points are (-2, -2) and (2, 0)
m = \(\frac { 0 + 2 }{ 2 + 2 } \) = \(\frac { 1 }{ 2 } \)
The equation is y – 2 = \(\frac { 1 }{ 2 } \)(x – 0)
y = \(\frac { 1 }{ 2 } \)x + 2
y = \(\frac { 1 }{ 2 } \)x + 2 for x > -2
Use the points (-2, -2) and (-4, -6)
m = \(\frac { -6 + 2 }{ -4 + 2 } \) = 2
y + 2 = 2(x + 2)
y = 2x + 2 for x < -2
Question 27.
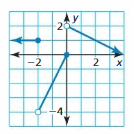
Answer:
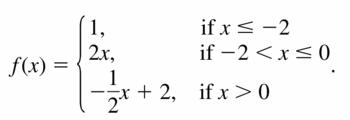
Question 28.
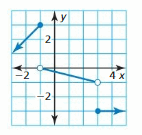
Answer:
The points are (-1, 3), (-2, 2)
m = \(\frac { 2 – 3 }{ -2 + 1 } \) = 1
y – y1 = m(x – x1)
y – 2 = 1(x + 2)
y = x – 4 for x < -1
Use the points (-2, 0) and (3, -1)
m = \(\frac { -1 – 0 }{ 3 + 2 } \) = \(\frac { -1 }{ 5 } \)
y – 0 = \(\frac { -1 }{ 5 } \)(x + 2)
y = \(\frac { -1 }{ 5 } \)(x + 2) for -2 > x < 3
y = -3 for x > 3
Question 29.
Answer:
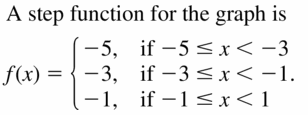
Question 30.
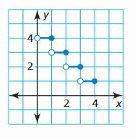
Answer:
y = 1 for 4 < x < 3
y = 2 for 3 < x < 2
y = 3 for 2 < x < 1
y = 4 for 1 < x < 0
In Exercises 31–34, graph the step function. Describe the domain and range.
Question 31.
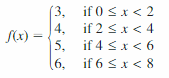
Answer:
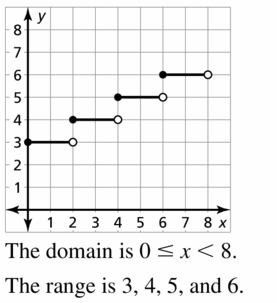
Question 32.
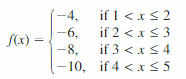
Answer:
Question 33.
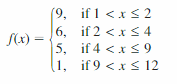
Answer:
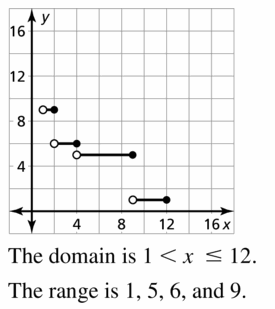
Question 34.
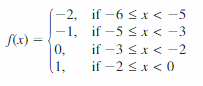
Answer:
Question 35.
MODELING WITH MATHEMATICS
The cost to join an intramural sports league is $180 per team and includes the first five team members. For each additional team member, there is a $30 fee. You plan to have nine people on your team. Write and graph a step function that represents the relationship between the number p of people on your team and the total cost of joining the league.
Answer:
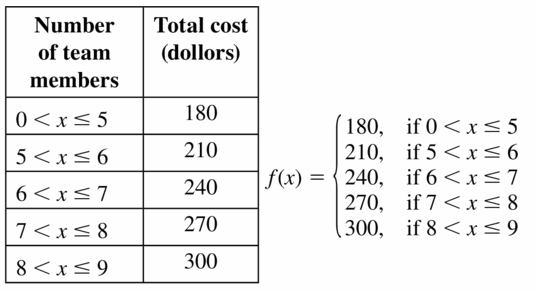
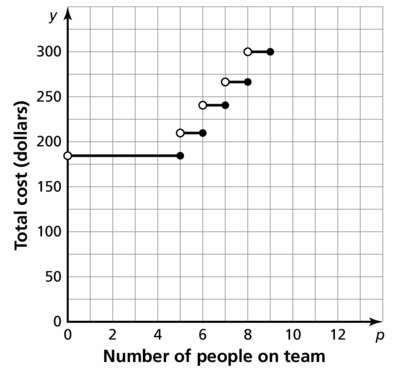
Question 36.
MODELING WITH MATHEMATICS
The rates for a parking garage are shown. Write and graph a step function that represents the relationship between the number x of hours a car is parked in the garage and the total cost of parking in the garage for 1 day.

Answer:
In Exercises 37–46, write the absolute value function as a piecewise function.
Question 37.
y = | x | + 1
Answer:
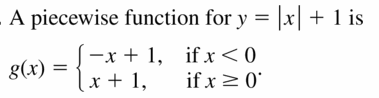
Question 38.
y = | x | – 3
Answer:
Given,
y = | x | – 3
A piecewise function is
g(x) = {-x – 3, if < 0
x – 3, if x ≥ 0
Question 39.
y = | x – 2 |
Answer:
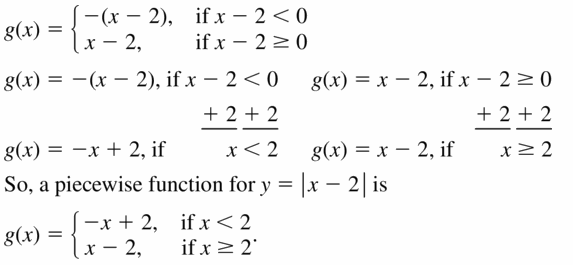
Question 40.
y = | x + 5 |
Answer:
Given
y = | x + 5 |
g(x) = { -(x + 5), if x + 5 < 0
x + 5, if x + 5 ≥ 0
i.e g(x) = {-x – 5, if x < -5
x + 5, if x ≥ -5
Question 41.
y = 2 | x + 3 |
Answer:
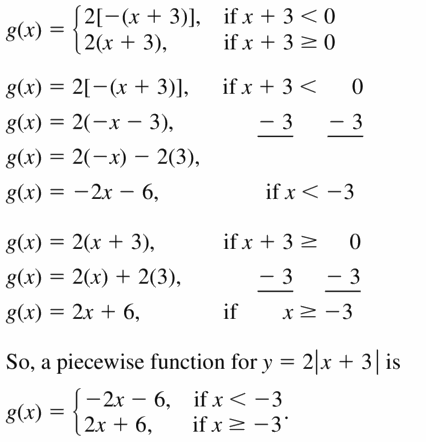
Question 42.
y = 4 | x – 1 |
Answer:
Given,
y = 4 | x – 1 |
g(x) = {-4(x – 1), if 4(x – 1) < 0 and 4(x – 1), if 4(x – 1) ≥ 0
g(x) = {4 -4x, if x < 1
4x – 4, if x ≥ 1
Question 43.
y = -5 | x – 8 |
Answer:
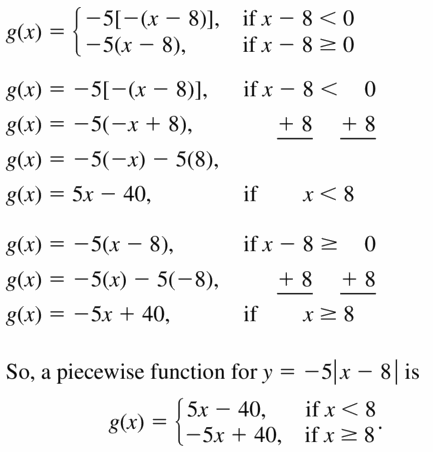
Question 44.
y = -3 | x + 6 |
Answer:
Given,
y = -3 | x + 6 |
g(x) = {3(x + 6), if -3(x+6) < 0 and -3(x + 6), if -3(x+6) ≥ 0
g(x) = {3(x + 6), if x < -2
-3(x + 6), if x ≥ -2
Question 45.
y = – | x – 3 | + 2
Answer:
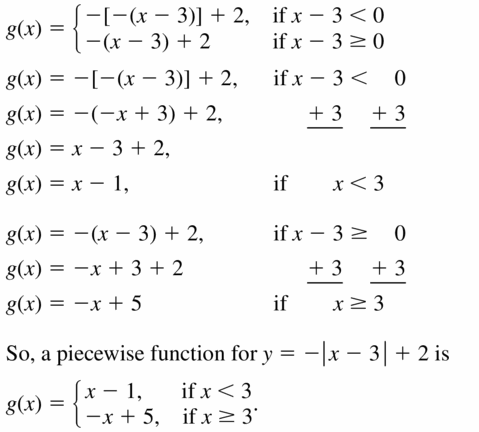
Question 46.
y = 7| x + 1 | – 5
Answer:
Given,
y = 7| x + 1 | – 5
g(x) = -7(x + 1) – 5, if 7(x + 1) – 5 < 0
7(x + 1) – 5, if 7(x + 1) – 5 ≥ 0
g(x) = {-7x – 13, if x < -2/7
7x + 2 , if x ≥ -2/7
Question 47.
MODELING WITH MATHEMATICS
You are sitting on a boat on a lake. You can get a sunburn from the sunlight that hits you directly and also from the sunlight that reflects off the water.
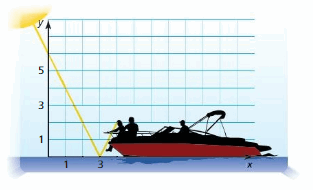
a. Write an absolute value function that represents the path of the sunlight that reflects off the water.
b. Write the function in part (a) as a piecewise function.
Answer:
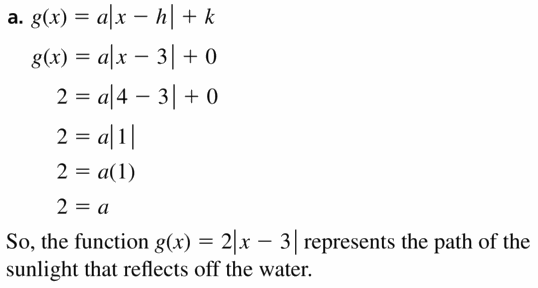
Question 48.
MODELING WITH MATHEMATICS
You are trying to make a hole in one on the miniature golf green.
a. Write an absolute value function that represents the path of the golf ball.
b. Write the function in part (a) as a piecewise function.
Answer:
The vertex of the path of the reference beam is (3, 0).
The function has the form g(x) = a|x – 3|.
Substitute the coordinates (5, 4)
4 = a|4 – 3|
4 = a
So, the function g(x) = 4|x – 3| represents the path of the reference beam
Question 49.
REASONING
The piecewise function f consists of two linear “pieces.” The graph of f is shown.
a. What is the value of f(-10)?
b. What is the value of f(8)?
Answer:
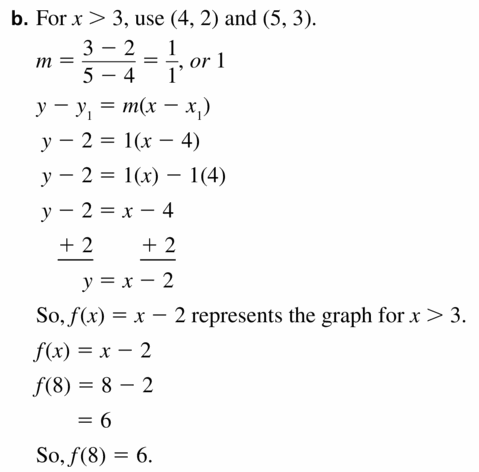
Question 50.
CRITICAL THINKING
Describe how the graph of each piecewise function changes when < is replaced with ≤ and ≥ is replaced with >. Do the domain and range change? Explain.
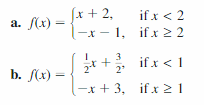
Answer:
Question 51.
USING STRUCTURE Graph
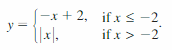
Describe the domain and range.
Answer:
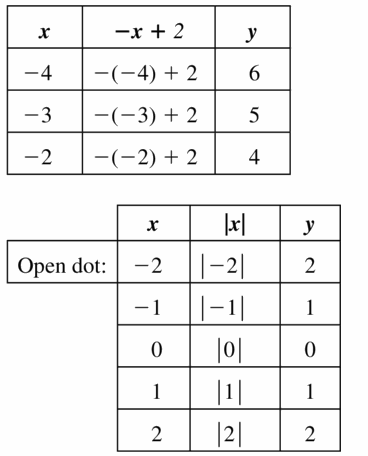
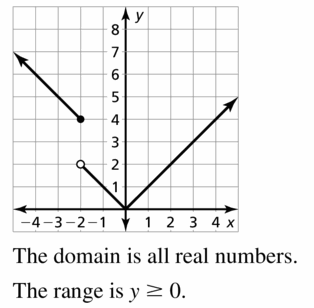
Question 52.
HOW DO YOU SEE IT? The graph shows the total cost C of making x photocopies at a copy shop.
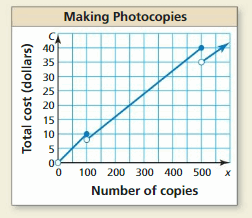
a. Does it cost more money to make 100 photocopies or 101 photocopies? Explain.
b. You have $40 to make photocopies. Can you buy more than 500 photocopies? Explain.
Answer:
C(x) = {0.15x, 0 < x ≤ 25,
0.10x, 25 < x ≤ 100,
0.07x, 100 < x ≤ 500,
0.05x, x > 500
Question 53.
USING STRUCTURE
The output y of the greatest integer function is the greatest integer less than or equal to the input value x. This function is written as ![]() . Graph the function for -4 ≤ x < 4. Is it a piecewise function? a step function? Explain.
. Graph the function for -4 ≤ x < 4. Is it a piecewise function? a step function? Explain.
Answer:
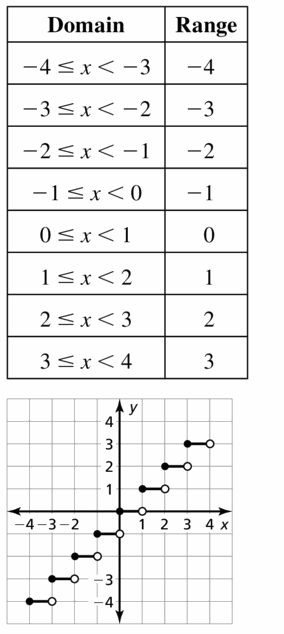

Question 54.
THOUGHT PROVOKING
Explain why
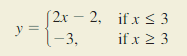
does not represent a function. How can you redefine y so that it does represent a function?
Answer:
Question 55.
MAKING AN ARGUMENT
During a 9-hour snowstorm, it snows at a rate of 1 inch per hour for the first 2 hours, 2 inches per hour for the next 6 hours, and 1 inch per hour for the final hour.
a. Write and graph a piecewise function that represents the depth of the snow during the snowstorm.
b. Your friend says 12 inches of snow accumulated during the storm. Is your friend correct? Explain.
Answer:

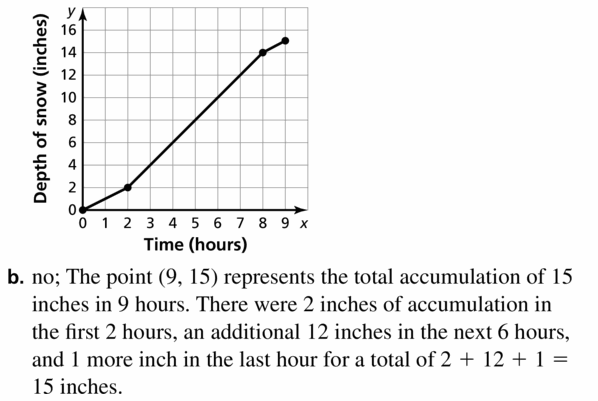
Maintaining Mathematical ProficiencyWrite the sentence as an inequality. Graph the inequality.(Section 2.5)
Question 56.
A number r is greater than -12 and no more than 13.
Answer:
A number r is greater than -12 and no more than 13.
r > -12
r ≤ 13
-12 < r ≤ 13

Question 57.
A number t is less than or equal to 4 or no less than 18.Graph f and h. Describe the transformations from the graph of f to the graph of h.(Section 3.6)
Answer:
Question 58.
f(x) = x; h(x) = 4x + 3
Answer:
Question 59.
f(x) = x; h(x) = -x – 8
Answer:
Question 60.
f(x) = x; h(x) = –\(\frac{1}{2}\) + 5
Answer:
Writing Linear Functions Performance Task: Any Beginning
4.4–4.7 What Did You Learn?
Core VocabularySection 4.4
![]()
Section 4.5
![]()
Section 4.6
![]()
Section 4.7
![]()
Mathematical Practices
Question 1.
What resources can you use to help you answer Exercise 17 on page 200?
Question 2.
What calculations are repeated in Exercises 11–16 on page 214? When finding a term such as a50, is there a general method or shortcut you can use instead of repeating calculations?
Question 3.
Describe the definitions you used when you explained your answer in Exercise 53 on page 224.
Performance TaskAny Beginning
With so many ways to represent a linear relationship, where do you start? Use what you know to move between equations, graphs, tables, and contexts.

To explore the answers to this question and more, go to 
Writing Linear Functions Chapter Review
Question 1.
Write an equation of the line in slope-intercept form.
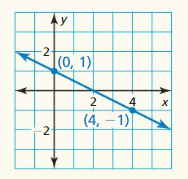
Answer:
m = \(\frac { -1 – 1 }{ 4 – 0 } \) = \(\frac { -1 }{ 2 } \)
y + 1 = \(\frac { -1 }{ 2 } \)(x – 4)
y + 1 = \(\frac { -1 }{ 2 } \)x + 2
y = \(\frac { -1 }{ 2 } \)x + 1
Question 2.
Write an equation in point-slope form of the line that passes through the point (4, 7) and has a slope of -1.
Answer:
Points = (4, 7)
m = -1
y – y1 = m(x – x1)
y – 7 = -1(x – 4)
y = -x + 4 + 7
y = -x + 11
Write a linear function f with the given values.
Question 3.
f(10) = 5, f(2) = -3
Answer:
Given,
f(10) = 5, f(2) = -3
The points are (10, 5), (2, -3)
m = \(\frac { -3 – 5 }{ 2 – 8 } \) = 1
The point-slope form of the line is (y – y₁) = m(x – x₁)
y – 5 = 1(x – 10)
y = x -10 + 5
y = x + 5
f = x + 5
Question 4.
f(3) = -4, f(5) = -4
Answer:
Given,
f(3) = -4, f(5) = -4
the points are (3, -4) and (5, -4)
The point-slope form of the line is (y – y₁) = m(x – x₁)
m = \(\frac { -4 + 4 }{ 5 – 3 } \) = 0
y + 4 = 0
y = -4
f(x) = -4
Question 5.
f(6) = 8, f(9) = 3
Answer:
Given,
f(6) = 8, f(9) = 3
The points are (8, 6) and (3, 9)
The point-slope form of the line is (y – y₁) = m(x – x₁)
m = \(\frac { 9 – 6 }{ 3 – 8 } \) = \(\frac { -3 }{ 5 } \)
y – 6 = \(\frac { -3 }{ 5 } \)(x – 8)
y = \(\frac { -3x }{ 5 } \) + \(\frac { 24 }{ 5 } \) + 6
y = \(\frac { -3x }{ 5 } \) + \(\frac { 54 }{ 5 } \)
Question 6.
Line a passes through (0, 4) and (4, 3).
Line b passes through (0, 1) and (4, 0).
Line c passes through (2, 0) and (4, 4).
Answer:
Line a:
Line a passes through (0, 4) and (4, 3).
(y – 4) = \(\frac { 3 – 4 }{ 4 – 0 } \)(x – 0)
y = \(\frac { -x }{ 4 } \) + 4
Line b:
Line b passes through (0, 1) and (4, 0).
(y – 1) = \(\frac { 0 – 1 }{ 4 – 0 } \)(x – 0)
y = \(\frac { -x }{ 4 } \) + 1
Line c:
Line c passes through (2, 0) and (4, 4).
y – 0 = \(\frac { 4 – 0 }{ 4 – 2 } \)(x – 2)
y = 2(x – 2)
Question 7.
Line a: 2x – 7y = 14
Line b: y = \(\frac{7}{2}\)x – 8
Line c: 2x + 7y = -21
Answer:
Line a: 2x – 14 = 7y
y = \(\frac { 2x }{ 7 } \) – 2
Line c: 7y = -21 – 2x
y = \(\frac { -2x }{ 7 } \) – 3
Lines b and c are perpendiculars
Question 8.
Write an equation of the line that passes through (1, 5) and is parallel to the line y = -4x + 2.
Answer:
Equation of the line that passes through (1, 5)
The line slope m = -4
y – 5 = -4(x – 1)
y – 5 = -4x + 4
y = -4x + 4 + 5
y = -4x + 9
Question 9.
Write an equation of the line that passes through (2, -3) and is perpendicular to the line y = -2x – 3
Answer:
The slope of the line m = \(\frac { 1 }{ 2 } \)
y – y1 = m(x – x1)
y + 3 = \(\frac { 1 }{ 2 } \)(x – 2)
y = \(\frac { 1 }{ 2 } \)x – 4
Question 10.
What is the roasting time for a 12-pound turkey?
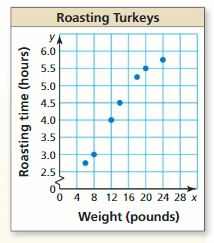
Answer:
The roasting time for a 12-pound turkey is 4.0 hours.
Question 11.
Write an equation that models the roasting time as a function of the weight of a turkey. Interpret the slope and y-intercept of the line of fit.
Answer:
(12, 4) and (20, 5.5)
(y – y1) = m(x – x1)
(y – 4) = \(\frac { 5.5 – 4 }{ 20 – 12 } \)(x – 12)
y – 4 = \(\frac { 1.5 }{ 8 } \)x – 2.25
y = \(\frac { 1.5 }{ 8 } \)x + 1.75
The y-intercept is 1.75 and slope is \(\frac { 1.5 }{ 8 } \)
Question 12.
Make a scatter plot of the residuals to verify that the model in the example is a good fit.
Answer:
Question 13.
Use the data in the example.
(a) Approximate the height of a student whose shoe size is 9.
Answer:
The height of the students whose shoe size is 9 is 9 = 0.5x – 23.5
0.5x = 32.5
x = 65
(b) Predict the shoe size of a student whose height is 60 inches.
Answer:
y = 0.5(60) – 23.5
y = 30 – 23.5 = 6.5
Question 14.
Is there a causal relationship in the data in the example? Explain.
write an equation for the nth term of the arithmetic sequence. Then find a30.
Question 15.
11, 10, 9, 8, …..
Answer:
Given sequence is 11, 10, 9, 8, …..
d = 10 – 11 = -1
an = 11 + (n – 1)(-1)
= 11 – n + 1 = 12 – n
a30 = 12 – 30 = -18
Question 16.
6, 12, 18, 24,….
Answer:
d = 12 – 6 = 6
an = 6 + (n – 1)(6)
= 6 + 6n – 6 = 6n
a30 = 6(30) = 180
Question 17.
-9, -6, -3, 0,….
Answer:
d = -6 + 9 = 3
an = -9 + (n – 1)3
= -9 + 3n – 3 = 3n – 12
a30 = 3(30) – 12 = 90 – 12 = 78
Question 18.
Evaluate the function in the example when (a) x = 0 and (b) x = 5.
Answer:
(a) f(x) = \(\frac { 3 }{ 2 } \)x + 3
f(0) = 3
(b) f(x) = -2x
f(5) = -2(5) = -10
Graph the function. Describe the domain and range.
Question 19.
![]()
Answer:
The domain is all real values and the range is -6.
Question 20.
![]()
Answer:
The domain is all real values and the range is 3.
Write the absolute value function as a piecewise function.
Question 21.
y =| x | + 15
Answer:
Given,
y =| x | + 15
g(x) = {-x + 15, if x + 15 < 0 and x + 15, if x + 15 ≥ 0
g(x) = {-x + 15, if x < -15
x + 15, if x ≥ -15
Question 22.
y = 4| x + 5 |
Answer:
Given,
y = 4| x + 5 |
g(x) = {-4(x + 5), if 4(x + 5) < 0 and 4(x + 5), if 4(x + 5) ≥ 0
g(x) = {-4(x + 5), if x < -5
4(x + 5), if x ≥ -5
Question 23.
y = 2 | x + 2 | – 3
Answer:
Given,
y = 2 | x + 2 | – 3
g(x) = {-2(x + 2) – 3, if 2(x + 2) – 3 < 0 and 2(x + 2) – 3, if 2(x + 2) – 3 ≥ 0
g(x) = {-2(x + 2) – 3, if x < -0.5
2(x + 2) – 3, if x > -0.5
Question 24.
You are organizing a school fair and rent a popcorn machine for 3 days. The rental company charges $65 for the first day and $35 for each additional day. Write and graph a step function that represents the relationship between the number x of days and the total cost y (in dollars) of renting the popcorn machine
Answer:
Given,
You are organizing a school fair and renting a popcorn machine for 3 days.
The rental company charges $65 for the first day and $35 for each additional day.
The rent for two days = 35 + 65 + 65 = 165
The rent for 3 days = 165 + 65 + 35 = 265
Writing Linear Functions Chapter Test
Graph the function. Describe the domain and range.
Question 1.
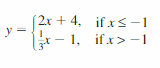
Question 2.
Write an equation in slope-intercept form of the line with the given characteristics.
Question 3.
slope = \(\frac{2}{5}\) ; y-intercept = -7
Answer:
y = mx + c
m = \(\frac{2}{5}\)
y-intercept = -7
y = \(\frac{2}{5}\)x – 7
Question 4.
passes through (0, 6) and (3, -3)
Answer:
Given,
passes through (0, 6) and (3, -3)
y – 6 = \(\frac{-3 – 6}{3 – 0}\)(x – 0)
y – 6 = -3x
y = -3x + 6
Question 5.
parallel to the line y = 3x – 1; passes through (-2, -8)
Answer:
y – y1 = m(x – x1)
y + 8 = 3(x + 2)
y + 8 = 3x + 6
y = 3x – 2
Question 6.
perpendicular to the line y = \(\frac{1}{4}\)x – 9; passes through (1, 1)
Answer:
y = \(\frac{1}{4}\)x – 9
passes through (1, 1)
y – y1 = m(x – x1)
y – 1 = -4(x – 1)
y = -4x + 4 + 1
y = -4x + 5
Write an equation in point-slope form of the line with the given characteristics.
Question 7.
slope = 10; passes through (6, 2)
Answer:
The point-slope form of the line is (y – y₁) = m(x – x₁)
y – 2 = 10(x – 6)
The equation is y – 2 = 10(x – 6)
Question 8.
passes through (-3, 2) and (6, -1)
Answer:
passes through (-3, 2) and (6, -1)
m = \(\frac { -1 – 2 }{ 6 + 3 } \) = \(\frac { -1 }{ 3 } \)
The point-slope form of the line is (y – y₁) = m(x – x₁)
y – 2 = \(\frac { -1 }{ 3 } \)(x + 3)
Question 9.
The first row of an auditorium has 42 seats. Each row after the first has three more seats than the row before it.
a. Find the number of seats in Row 25.
b. Which row has 90 seats?
Answer:
The first row of an auditorium has 42 seats. Each row after the first has three more seats than the row before it.
a. a25 = 42 + (25 – 1)3
= 42 + 24(3) = 114
The number of seats in row 25 are 114
b. 90 = 42 + (n – 1)3
48 = 3n – 3
3n = 51
n = 17
The 17th row has 90 seats.
Question 10.
The table shows the amount x (in dollars) spent on advertising for a neighborhood festival and the attendance y of the festival for several years.
a. Make a scatter plot of the data. Describe the correlation.
b. Write an equation that models the attendance as a function of the amount spent on advertising.
c. Interpret the slope and y-intercept of the line of fit.
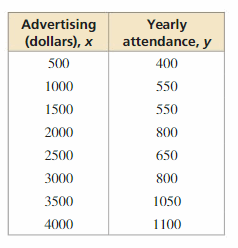
Answer:
a.
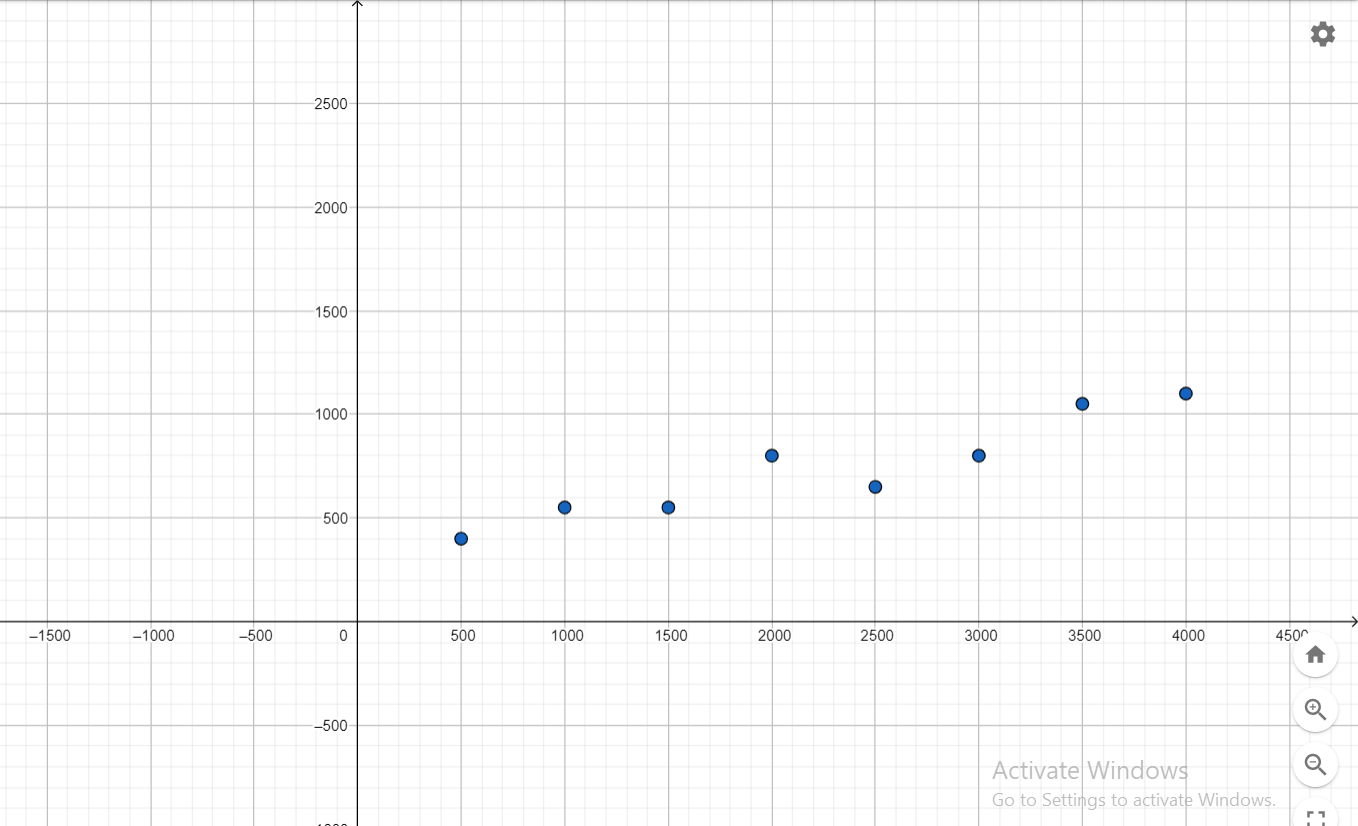
b. the points are (2000, 800) and (1500, 550)
(y – 800) = \(\frac { 550 – 800 }{ 1500 – 2000 } \)(x – 2000)
y – 800 = 0.5(x – 2000)
y = 0.5x – 1000 + 800
y = 0.5x – 200
c. slope is 0.5 and y-intercept is -200.
Question 11.
Consider the data in the table in Exercise 10.
a. Use a graphing calculator to find an equation of the line of best fit.
b. Identify and interpret the correlation coefficient.
c. What would you expect the scatter plot of the residuals to look like?
d. Is there a causal relationship in the data? Explain your reasoning.
e. Predict the amount that must be spent on advertising to get 2000 people to attend the festival.
Answer:
Question 12.
Let a, b, c, and d be constants. Determine which of the lines, if any, are parallel or perpendicular. Explain.
![]()
Answer:
Line 1: y = ax + c
Line 2: y = \(\frac { -x }{ a } \) – \(\frac { b }{ a } \)
Line 3: y = -ax + d
None of the lines are parallel or perpendicular.
Question 13.
Write a piecewise function defined by three equations that has a domain of all real numbers and a range of -3 < y ≤ 1.
Answer:
Writing Linear Functions Cumulative Assessment
Question 1.
Which function represents the arithmetic sequence shown in the graph?
A. f(n) = 15 + 3n
B. f(n) = 4 – 3
C. f(n) = 27 – 3n
D. f(n) = 24 – 3n
Answer:
C. f(n) = 27 – 3n
f(1) = 27 – 3 = 24
f(2) = 27 -6 = 21
f(3) = 27 – 9 = 18
Question 2.
Which of the inequalities are equivalent?
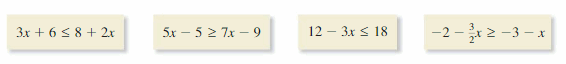
Answer:
3x + 6 ≤ 8 + 2x
3x – 2x ≤ 8 – 6
x ≤ 2
5x – 5 ≥ 7x – 9
-5 + 9 ≥ 7x – 5x
4 ≥ 2x
x ≥ 2
12 – 3x ≤ 18
-3x ≤ 18 – 12
-3x ≤ 6
x ≤ -2
x ≥ 2
-2 -3/2 x ≥ -3 – x
-3/2 x + x ≥ -3 + 2
-0.5x ≥ -1
x ≥ 2
5x – 5 ≥ 7x – 9, 12 – 3x ≤ 18, -2 -3/2 x ≥ -3 – x are equivalent.
Question 3.
Complete the table for the four situations below. Explain your reasoning.
a. the price of a pair of pants and the number sold
b. the number of cell phones and the number of taxis in a city
c. a person’s IQ and the time it takes the person to run 50 meters
d. the amount of time spent studying and the score earned
Answer:
Question 4.
Consider the function f(x) = x – 1. Select the functions that are shown in the graph. Explain your reasoning.
Answer:
g(x) = x + 2 – 1 = x + 1
h(x) = 3x – 1
k(x) = x – 1 + 4 = x + 3
p(x) = -x – 1
r(x) = 3(x – 1) = 3x – 3
q(x) = -(x – 1) = 1 – x
Question 5.
Use the numbers to fill in values for m and b in the equation y = mx + b so that its graph passes through the points (6, 1) and (-2, -3).
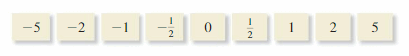
Answer:
slope m = \(\frac { -3 – 1 }{ -2 – 6 } \) = \(\frac { 1 }{ 2 } \)
y – 1 = \(\frac { 1 }{ 2 } \)(x – 6)
y = \(\frac { 1 }{ 2 } \)x – 3 + 1
y = \(\frac { 1 }{ 2 } \)x – 2
Question 6.
Fill in the piecewise function with -, +, <, ≤, >, or ≥ so that the function is represented by the graph.
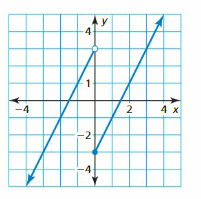
Answer:
y = {2x – 3, if x < 0
2x – 3, if x > 0
Question 7.
You claim that you can create a relation that is a function, and your friend claims that she can create a relation that is not a function. Using the given numbers, create a relation of five ordered pairs that supports your claim. What relation of five ordered pairs can your friend use to support her claim?
Answer:
Question 8.
You have two coupons you can use at a restaurant. Write and solve an equation to determine how much your total bill must be for both coupons to save you the same amount of money.

Answer:
Let the total purchase is $x
By using the first coupon of 20%, we get a discount of x/5
This discount must be equal to $5 as a discount on the second coupon
x/5 = 5
x = 25
The total bill is $25.
Question 9.
The table shows the daily high temperatures x (in degrees Fahrenheit) and the numbers y of frozen fruit bars sold on eight randomly selected days. The equation y = 3x – 50 models the data.

a. Select the points that appear on a scatter plot of the residuals.

b. Determine whether the model is a good fit for the data. Explain your reasoning.
Answer:
a.
| x | y | y value from the model | residual |
|---|---|---|---|
| 54 | 40 | 112 | 40 – 112 = -72 |
| 60 | 120 | 130 | 120 – 130 = -10 |
| 68 | 180 | 154 | 180 – 154 = 26 |
| 72 | 260 | 166 | 260 – 166 = 94 |
| 78 | 280 | 184 | 280 – 184 = 96 |
| 84 | 260 | 202 | 260 – 202 = 58 |
| 92 | 220 | 226 | 220 – 226 = -6 |
| 98 | 180 | 244 | 180 – 244 = -64 |
(92, -6), (78, 96), (60, -10), (84, 58), (98, -64), (72, 94), (54, -72), (68, 26)
b. 
The points are not above the x-axis. So the model does not fill well.