Solve simple concepts of Rational Exponents and Radical Functions by practicing problems from Big Ideas Math Algebra 2 Answers? Get free access to download Big Ideas Math Algebra 2 Answers Chapter 5 Rational Exponents and Radical Functions from this page. You may have doubts about the solutions don’t worry our subject experts created this BIM algebra 2 ch 5 solution key as per the Common core student edition BIM Algebra 2 Textbooks. Improve your preparation level with the help of Big Ideas Math Book Algebra 2 Chapter 5 Answer Key.
Big Ideas Math Book Algebra 2 Answer Key Chapter 5 Rational Exponents and Radical Functions
Get the direct links of Big Ideas Math Book Algebra 2 Answer Key Chapter 5 Rational Exponents and Radical Functions prevailing in order to help the students and teachers. Quick and easy learning is possible with our BIM Algebra 2 Book Solutions of ch 5 Rational Exponents and Radical Functions. With the help of Big Ideas Math Book Algebra 2 Answer Key Chapter 5 Rational Exponents and Radical Functions, you can score good marks in the exams. Test your math skills by solving the questions provided at the end of this chapter. Click on the links such as chapter tests, reviews, practices, quizzes, cumulative assessments, etc to check your answers.
- Rational Exponents and Radical Functions Maintaining Mathematical Proficiency – Page 235
- Rational Exponents and Radical Functions Mathematical Practices – Page 236
- Lesson 5.1 nth Roots and Rational Exponents – Page(238-242)
- nth Roots and Rational Exponents 5.1 Exercises – Page(241-242)
- Lesson 5.2 Properties of Rational Exponents and Radicals – Page(244-250)
- Properties of Rational Exponents and Radicals 5.2 Exercises – Page(248-250)
- Lesson 5.3 Graphing Radical Functions – Page(252-258)
- Graphing Radical Functions 5.3 Exercises – Page(256-258)
- Rational Exponents and Radical Functions Study Skills – Page 259
- Rational Exponents and Radical Functions 5.1 – 5.3 Quiz – Page 260
- Lesson 5.4 Solving Radical Equations and Inequalities – Page(262-268)
- Solving Radical Equations and Inequalities 5.4 Exercises – Page(266-268)
- Lesson 5.5 Performing Function Operations – Page(270-274)
- Performing Function Operations 5.5 Exercises – Page(273-274)
- Lesson 5.6 Inverse of a Function – Page(276-284)
- Inverse of a Function 5.6 Exercises – Page(281-284)
- Rational Exponents and Radical Functions Performance Task – Page 285
- Rational Exponents and Radical Functions Chapter Review – Page(286-288)
- Rational Exponents and Radical Functions Chapter Test – Page 289
- Rational Exponents and Radical Functions Cumulative Assessment – Page(290-291)
Rational Exponents and Radical Functions Maintaining Mathematical Proficiency
Simplify the expression
Question 1.
y6 • y
Answer: y7
Explanation:
Given,
y6 • y
When bases are equal powers should be added.
am . an = am+n
y6 • y = y6+1 = y7
Question 2.
\(\frac{n^{4}}{n^{3}}\)
Answer: n
Explanation:
Given,
\(\frac{n^{4}}{n^{3}}\)
am / an = am-n
= n4-3
= n¹
So, \(\frac{n^{4}}{n^{3}}\) = n
Question 3.
\(\frac{x^{5}}{x^{6} \cdot x^{2}}\)
Answer: n-3
Explanation:
Given,
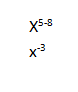
Question 4.
\(\frac{x^{-6}}{x^{5}}\) • 3x²
Answer: 3x-9
Explanation:
Given,
\(\frac{x^{-6}}{x^{5}}\) • 3x²
am / an = am-n
= x-6-5 . 3x²
= x-11 . 3x²
= 3x-9
So, \(\frac{x^{-6}}{x^{5}}\) • 3x² = 3x-9
Question 5.
\(\left(\frac{4 w^{3}}{2 z^{2}}\right)^{3}\)
Answer: \(\left(\frac{2 w^{3}}{z^{2}}\right)^{3}\)
Explanation:
Given,
\(\left(\frac{4 w^{3}}{2 z^{2}}\right)^{3}\)
4/2 = 2
\(\left(\frac{2 w^{3}}{z^{2}}\right)^{3}\)
Question 6.
\(\left(\frac{m^{7} \cdot m}{z^{2} \cdot m^{3}}\right)^{2}\)
Answer: (m5/z²)²
Explanation:
Given,
\(\left(\frac{m^{7} \cdot m}{z^{2} \cdot m^{3}}\right)^{2}\)
= (m8/z²m³)²
= (m5/z²)²
So, \(\left(\frac{m^{7} \cdot m}{z^{2} \cdot m^{3}}\right)^{2}\) = (m5/z²)²
Solve the literal equation for y.
Question 7.
4x + y = 2
Answer: 2 – 4x
Explanation:
Given,
4x + y = 2
Rewrite the equation so a different variable stands alone on one side of the equal sign.
We have to make y the subject.
y = 2 – 4x
So, the equation for y is 2 – 4x.
Question 8.
x − \(\frac{1}{3}\)y = −1
Answer: 3(x + 1)
Explanation:
Given,
x − \(\frac{1}{3}\)y = −1
Rewrite the equation so a different variable stands alone on one side of the equal sign.
Make y as the subject.
− \(\frac{1}{3}\)y = -1 – x
-(\(\frac{1}{3}\)y = -(1 + x)
\(\frac{1}{3}\)y = x + 1
y = 3(x + 1)
So, the equation for y is 3(x + 1).
Question 9.
2y − 9 = 13x
Answer:
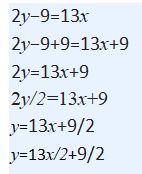
Question 10.
2xy + 6y = 10
Answer: 5/3 + x
Explanation:
Given,
2xy+6y=10
Take 2 as the common factor.
2(xy+3y)=2(5)
Divide by 2 on both sides.
2(xy+3y)/2=2(5)/2
xy+3y=5xy+3y
=5xy+3y=5
Rewrite the equation so a different variable stands alone on one side of the equal sign.
Make y as the subject.
y(x+3)=5
y(x+3)/x+3 = 5/3+x
y = 5/3 + x
So, the equation for y is 5/3 + x
Question 11.
8x − 4xy = 3
Answer: -3/4x+2
Explanation:
Given,
8x − 4xy = 3
Apply inverse operations to isolate
8x−4xy=3
4x(2−y)=3
Rewrite the equation so a different variable stands alone on one side of the equal sign.
Make y as the subject.
2−y=3/4x
–y=3/4x−2
y=–1(3/4x−2)
y=-3/4x+2
So, the equation for y is -3/4x+2
Question 12.
6x + 7xy = 15
Answer: (15 – 6x)/7x
Explanation:
Given,
6x + 7xy = 15
Rewrite the equation so a different variable stands alone on one side of the equal sign.
Make y as the subject.
7xy = 15 – 6x
y = (15 – 6x)/7x
So, the equation for y is (15 – 6x)/7x
Question 13.
ABSTRACT REASONING Is the order in which you apply properties of exponents important? Explain your reasoning.
Answer: Exponents are values that are powers that show how many times we have to multiply the base number by itself. The exponents are important to write the values of numbers in a simplified form.
The properties of the exponent are
1. Product of powers
2. Quotient of powers
3. Power to a power
4. Power of a product
5. Power of a quotient
Rational Exponents and Radical Functions Mathematical Practices
Monitoring Progress
Question 1.
Use the Pythagorean Theorem to find the exact lengths of a, b, c, and d in the figure.
Question 2.
Use a calculator to approximate each length to the nearest tenth of an inch.
Answer:
We can find the length and angle measured to the nearest tenth using the calculator.
a = √2
a = 1.414
a ≈ 1.41
b = √3
b = 1.732
b ≈ 1.73
c = 2
c is the whole number
d = √5
d = 2.2360
d ≈ 2.24
Question 3.
Use a ruler to check the reasonableness of your answers.
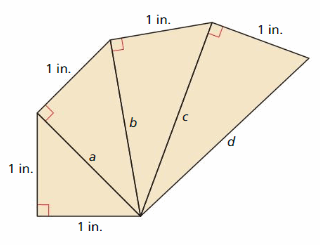
Answer:
a = √2
b = √3
c = 2
d = √5
Explanation:
Given,
s = 1 in.
1² + 1² = a²
a = √1 + 1
a = √2
The measure of hypotenuse a is √2.
√2² + 1² = b²
2 + 1 = b²
b² = 3
b = √3
The measure of hypotenuse b is √3.
√3² + 1² = c²
c² = 3 + 1
c² = 4
c = 2
The measure of hypotenuse c is 2.
2² + 1² = d²
d² = 4 + 1
d² = 5
d = √5
The measure of hypotenuse d is √5.
Lesson 5.1 nth Roots and Rational Exponents
Essential Question
How can you use a rational exponent to represent a power involving a radical?
Previously, you learned that the nth root of a can be represented as
\(\sqrt[n]{a}\) = \(a^{1 / n}\) Definition of rational exponent
for any real number a and integer n greater than 1.
EXPLORATION 1
Exploring the Definition of a Rational Exponent
Work with a partner. Use a calculator to show that each statement is true.
a. \(\sqrt{9}\) = \(9^{1 / 2}\)
Answer:
Given,
\(\sqrt{9}\) = \(9^{1 / 2}\)
In order to rewrite a radical using a fractional exponent, the power to which the radicand becomes the numerator and the root becomes the denominator.
Square is nothing but 2.
So, \(\sqrt{9}\) can be written in the fractional exponent as \(9^{1 / 2}\).
The statement \(\sqrt{9}\) = \(9^{1 / 2}\) is true.
b. \(\sqrt{2}\) = \(2^{1 / 2}\)
Answer:
Given,
\(\sqrt{2}\) = \(2^{1 / 2}\)
In order to rewrite a radical using a fractional exponent, the power to which the radicand becomes the numerator and the root becomes the denominator.
Square is nothing but 2.
So, \(\sqrt{2}\) can be written in the fractional exponent as \(2^{1 / 2}\).
The statement is true.
c. \(\sqrt[3]{8}\) = \(8^{1 / 3}\)
Answer:
Given,
\(\sqrt[3]{8}\) = \(8^{1 / 3}\)
In order to rewrite a radical using a fractional exponent, the power to which the radicand becomes the numerator and the root becomes the denominator.
Cube root is nothing but 1/3.
\(\sqrt[3]{8}\) can be written in the fractional exponent as \(8^{1 / 3}\).
The statement is true.
d. \(\sqrt[3]{3}\) = \(3^{1 / 3}\)
Answer:
Given,
\(\sqrt[3]{3}\) = \(3^{1 / 3}\)
In order to rewrite a radical using a fractional exponent, the power to which the radicand becomes the numerator and the root becomes the denominator.
Cube root is nothing but 1/3.
\(\sqrt[3]{3}\) can be written in the fractional exponent as \(3^{1 / 3}\).
The statement is true.
e. \(\sqrt[4]{16}\) = \(16^{1 / 4}\)
Answer:
Given,
\(\sqrt[4]{16}\) = \(16^{1 / 4}\)
In order to rewrite a radical using a fractional exponent, the power to which the radicand becomes the numerator and the root becomes the denominator.
The fourth root is nothing but 1/4.
\(\sqrt[4]{16}\) can be written in the fractional exponent as \(16^{1 / 4}\).
The statement is true.
f. \(\sqrt[4]{12}\) = \(12^{1 / 4}\)
Answer:
Given,
\(\sqrt[4]{12}\) = \(12^{1 / 4}\)
In order to rewrite a radical using a fractional exponent, the power to which the radicand becomes the numerator and the root becomes the denominator.
The fourth root is nothing but 1/4.
\(\sqrt[4]{12}\) can be written in the fractional exponent as \(12^{1 / 4}\).
EXPLORATION 2
Writing Expressions in Rational Exponent Form

Work with a partner. Use the definition of a rational exponent and the properties of exponents to write each expression as a base with a single rational exponent. Then use a calculator to evaluate each expression. Round your answer to two decimal places.

a. \((\sqrt{5})^{3}\)
Answer: 11.08
Explanation:
Given,
\((\sqrt{5})^{3}\)
The square root of 5 is 2.23
(\(\sqrt{5}\))³ = (2.23)³ = 11.08
b. \((\sqrt[4]{4})^{2}\)
Answer: 1.99
Explanation:
Given,
\((\sqrt[4]{4})^{2}\)
The fourth root of 4 is 1.414
\((\sqrt[4]{4})^{2}\) = (1.414)² = 1.99
c. \((\sqrt[3]{9})^{2}\)
Answer: 4.32
Explanation:
Given,
\((\sqrt[3]{9})^{2}\)
The cube root of 9 is 2.08
\((\sqrt[3]{9})^{2}\) = (2.08)² = 4.32
d. \((\sqrt[5]{10})^{4}\)
Answer: 6.23
Explanation:
Given,
\((\sqrt[5]{10})^{4}\)
The fifth root of 10 is 1.58
\((\sqrt[5]{10})^{4}\) = (1.58)4 = 6.23
e. \((\sqrt{15})^{3}\)
Answer: 57.96
Explanation:
Given,
\((\sqrt{15})^{3}\)
the square root of 15 is 3.87
\((\sqrt{15})^{3}\) = (\(\sqrt{15}\))³ = (3.87)³ = 57.96
f. \((\sqrt[3]{27})^{4}\)
Answer: 81
Explanation:
Given,
\((\sqrt[3]{27})^{4}\)
The cube root of 27 is 3.
\((\sqrt[3]{27})^{4}\) = (3)4 = 81
EXPLORATION 3
Writing Expressions in Radical Form
Work with a partner. Use the properties of exponents and the definition of a rational exponent to write each expression as a radical raised to an exponent. Then use a calculator to evaluate each expression. Round your answer to two decimal places.
Sample \(5^{2 / 3}\) = (\left(5^{1 / 3}\right)\(\))2 = (\((\sqrt[3]{5})\))2 ≈ 2.92
a. \(8^{2 / 3}\)
b. \(6^{5 / 2}\)
c. \(12^{3 / 4}\)
d. \(10^{3 / 2}\)
e. \(16^{3 / 2}\)
f. \(20^{6 / 5}\)
Answer:
a. \(8^{2 / 3}\) = (\((\sqrt[3]{8})\))²
The cube root of 8 is 2.
= 2² = 4
b. \(6^{5 / 2}\) = (\((\sqrt[5]{6})\))²
The fifth root of 6 is 1.43
= (1.43)² = 2.04
c. \(12^{3 / 4}\)
The cube root of 12 is 2.28
= (\((\sqrt[3]{12})\))4 = (2.28)4 = 27.02
d. \(10^{3 / 2}\)
The cube root of 10 is 2.15
= (\((\sqrt[3]{10})\))² =(2.15)² = 4.62
e. \(16^{3 / 2}\)
The cube root of 16 is 2.51
= (\((\sqrt[3]{16})\))² = (2.51)² = 6.3
f. \(20^{6 / 5}\)
The sixth root of 20 is 1.82
= (\((\sqrt[6]{20})\))5 = (1.82)5 = 19.96
Communicate Your Answer
Question 4.
How can you use a rational exponent to represent a power involving a radical?
Answer:
In order to rewrite a radical using a fractional exponent, the power to which the radicand becomes the numerator and the root becomes the denominator. Any power can be written in the fractional exponent form.
Question 5.
Evaluate each expression without using a calculator. Explain your reasoning.
a. \(4^{3 / 2}\)
b. \(32^{4 / 5}\)
c. \(625^{3 / 4}\)
d. \(49^{3 / 2}\)
e. \(125^{4 / 3}\)
f. \(100^{6 / 3}\)
Answer:
a. \(4^{3 / 2}\)
= 41/2
= 2
= 2³ = 8
So, \(4^{3 / 2}\) = 8
b. \(32^{4 / 5}\)
= 321/5×4
= 25(1/5×4)
= (2)4 = 16
So, \(32^{4 / 5}\) = 16
c. \(625^{3 / 4}\)
= 6251/4×3
= (625)1/4 = 5
= (5)³ = 125
d. \(49^{3 / 2}\)
= 491/2 = 7
= (7)³= 343
So, \(49^{3 / 2}\) = 343
e. \(125^{4 / 3}\)
= 1251/3
= (5)4 = 625
So, \(125^{4 / 3}\) = 625
f. \(100^{6 / 3}\)
= 1001/3
= 4.64
= (4.64)6 = 9979.
So, \(100^{6 / 3}\) = 9979
5.1 Lesson
Monitoring Progress
Question 1.
n = 4, a = 16
Answer:

Question 2.
n = 2, a = −49
Answer:

Question 3.
n = 3, a = −125
Answer:
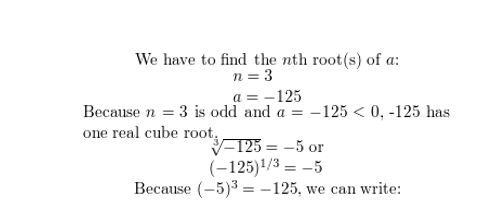
Question 4.
n = 5, a = 243
Answer:

Evaluate the expression without using a calculator.
Question 5.
\(4^{5 / 2}\)
Answer:

Question 6.
\(9^{-1 / 2}\)
Answer:

Question 7.
\(81^{3 / 4}\)
Answer:

Question 8.
\(1^{7 / 8}\)
Answer:
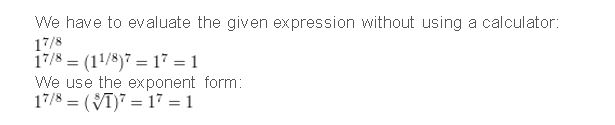
Evaluate the expression using a calculator. Round your answer to two decimal places when appropriate.
Question 9.
\(6^{2 / 5}\)
Answer:

Question 10.
\(64^{-2 / 3}\)
Answer:

Question 11.
\((\sqrt[4]{16})^{5}\)
Answer:

Question 12.
\((\sqrt[3]{-30})^{2}\)
Answer:

Find the real solution(s) of the equation. Round your answer to two decimal places when appropriate.
Question 13.
8x3 = 64
Answer:

Question 14.
\([\frac{1}{2}/latex]x5 = 512
Answer:

Question 15.
(x + 5)4 = 16
Answer:

Question 16.
(x − 2)3 = −14
Answer:

Question 17.
WHAT IF? In Example 5, what is the annual depreciation rate when the salvage value is $6000?
Answer:

nth Roots and Rational Exponents 5.1 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY Rewrite the expression [latex]a^{-s / t}\) in radical form. Then state the index of the radical.
Answer:
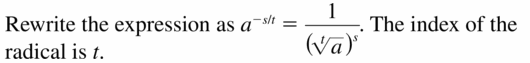
Question 2.
COMPLETE THE SENTENCE For an integer n greater than 1, if bn = a, then b is a(n) ___________ of a.
Answer:

Question 3.
WRITING Explain how to use the sign of a to determine the number of real fourth roots of a and the number of real fifth roots of a.
Answer:
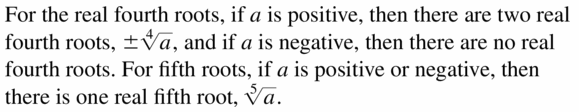
Question 4.
WHICH ONE DOESN’T BELONG? Which expression does not belong with the other three? Explain your reasoning.

Answer:
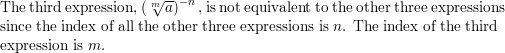
Monitoring Progress and Modeling with Mathematics
In Exercises 5–10, find the indicated real nth root(s) of a.
Question 5.
n = 3, a = 8
Answer:
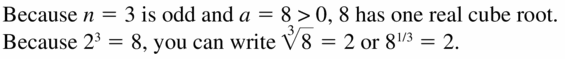
Question 6.
n = 5, a = −1
Answer:

Question 7.
n = 2, a = 0
Answer:
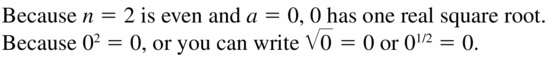
Question 8.
n = 4, a = 256
Answer:
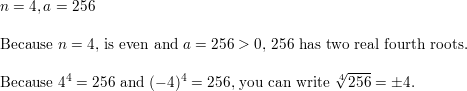
Question 9.
n = 5, a = −32
Answer:
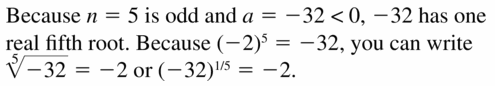
Question 10.
n = 6, a = −729
Answer:

In Exercises 11–18, evaluate the expression without using a calculator.
Question 11.
\(64^{1 / 6}\)
Answer:
![]()
Question 12.
\(8^{1 / 3}\)
Answer:
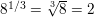
Question 13.
\(25^{3 / 2}\)
Answer:
![]()
Question 14.
\(81^{3 / 4}\)
Answer:

Question 15.
\((-243)^{1 / 5}\)
Answer:
![]()
Question 16.
\((-64)^{4 / 3}\)
Answer:
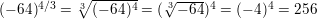
Question 17.
\(8^{-2 / 3}\)
Answer:
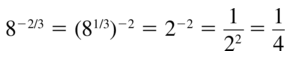
Question 18.
\(16^{-7 / 4}\)
Answer:
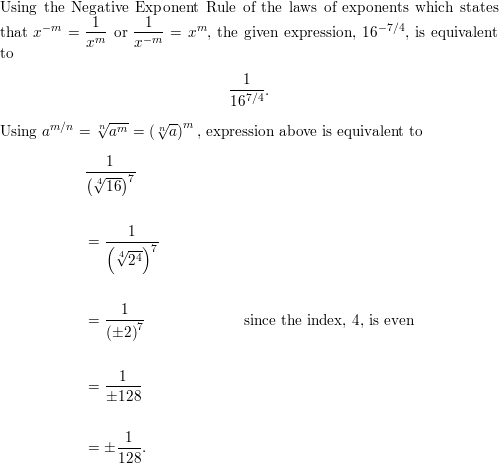
ERROR ANALYSIS In Exercises 19 and 20, describe and correct the error in evaluating the expression.
Question 19.

Answer:
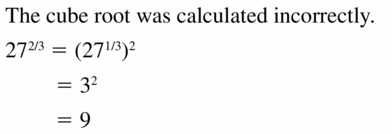
Question 20.
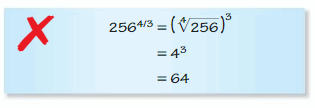
Answer:
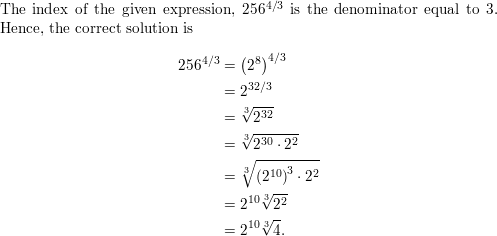
USING STRUCTURE In Exercises 21–24, match the equivalent expressions. Explain your reasoning.
Question 21.
\((\sqrt[3]{5})^{4}\) A. \(5^{-1 / 4}\)
Answer:
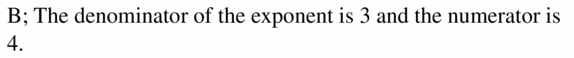
Question 22.
\((\sqrt[4]{5})^{3}\) B. \(5^{4 / 3}\)
Answer:
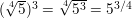
Question 23.
\(\frac{1}{\sqrt[4]{5}}\) C. \(-5^{1 / 4}\)
Answer:
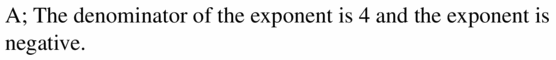
Question 24.
\(-\sqrt[4]{5}\) D. \(5^{3 / 4}\)
Answer:
In Exercises 25–32, evaluate the expression using a calculator. Round your answer to two decimal places when appropriate.
Question 25.
\(\sqrt[5]{32,768}\)
Answer:
![]()
Question 26.
\(\sqrt[7]{1695}\)
Answer:
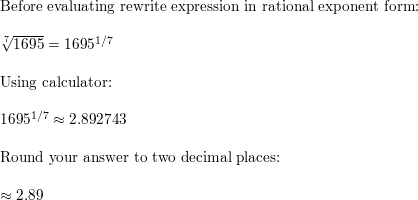
Question 27.
\(25^{-1 / 3}\)
Answer:
![]()
Question 28.
\(85^{1 / 6}\)
Answer:

Question 29.
\(20,736^{4 / 5}\)
Answer:
![]()
Question 30.
\(86^{-5 / 6}\)
Answer:

Question 31.
\((\sqrt[4]{187})^{3}\)
Answer:
![]()
Question 32.
\((\sqrt[5]{-8})^{8}\)
Answer:

MATHEMATICAL CONNECTIONS In Exercises 33 and 34, find the radius of the figure with the given volume.
Question 33.
V = 216 ft3
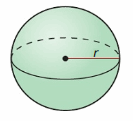
Answer:

Question 34.
V = 1332 cm3
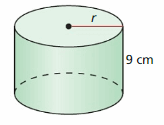
Answer:

In Exercises 35–44, find the real solution(s) of the equation. Round your answer to two decimal places when appropriate.
Question 35.
x3 = 125
Answer:

Question 36.
5x3 = 1080
Answer:
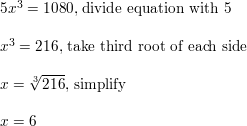
Question 37.
(x + 10)5 = 70
Answer:
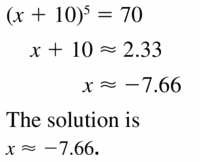
Question 38.
(x − 5)4 = 256
Answer:
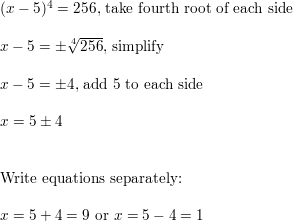
Question 39.
x5 = −48
Answer:
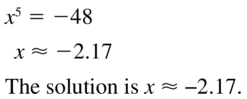
Question 40.
7x4 = 56
Answer:

Question 41.
x6 + 36 = 100
Answer:
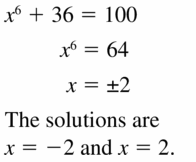
Question 42.
x3 + 40 = 25
Answer:

Question 43.
\(\frac{1}{3}\)x4 = 27
Answer:
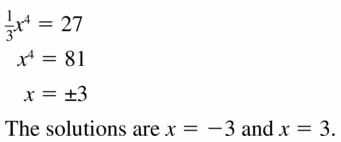
Question 44.
\(\frac{1}{6}\)x3 = −36
Answer:

Question 45.
MODELING WITH MATHEMATICS When the average price of an item increases from p1 to p2 over a period of n years, the annual rate of inflation r (in decimal form) is given by r = \(\left(\frac{p_{2}}{p_{1}}\right)^{1 / n}\) − 1. Find the rate of inflation for each item in the table.
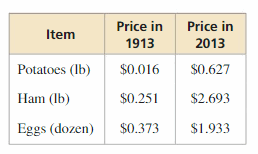
Answer:

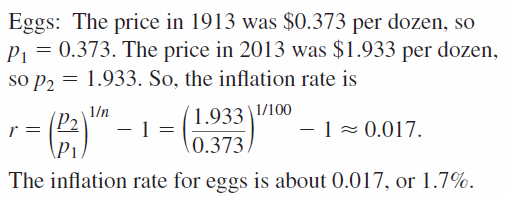
Question 46.
HOW DO YOU SEE IT? The graph of y = xn is shown in red. What can you conclude about the value of n? Determine the number of real nth roots of a. Explain your reasoning.
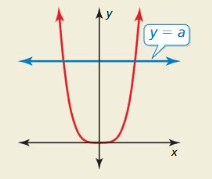
Answer:

Question 47.
NUMBER SENSE Between which two consecutive integers does \(\sqrt[4]{125}\) lie? Explain your reasoning.
Answer:
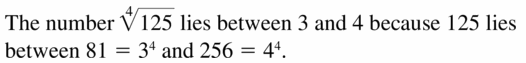
Question 48.
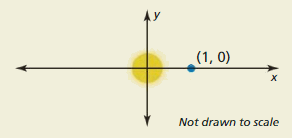
THOUGHT PROVOKING In 1619, Johannes Kepler published his third law, which can be given by d3 = t2, where d is the mean distance (in astronomical units) of a planet from the Sun and t is the time (in years) it takes the planet to orbit the Sun. It takes Mars 1.88 years to orbit the Sun. Graph a possible location of Mars. Justify your answer. (The diagram shows the Sun at the origin of the xy-plane and a possible location of Earth.)
Answer:
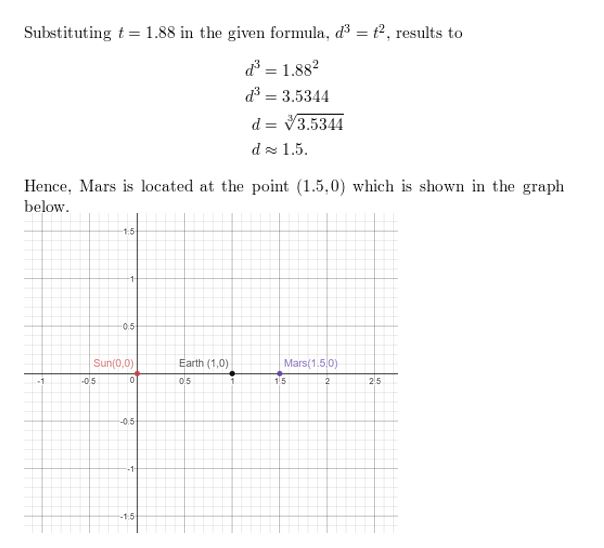
Question 49.
PROBLEM SOLVING A weir is a dam that is built across a river to regulate the flow of water. The flow rate Q (in cubic feet per second) can be calculated using the formula Q= 3.367ℓ\(h^{3 / 2}\), where ℓ is the length (in feet) of the bottom of the spillway and his the depth (in feet) of the water on the spillway. Determine the flow rate of a weir with a spillway that is 20 feet long and has a water depth of 5 feet.

Answer:
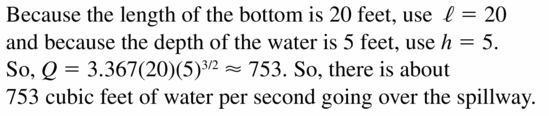
Question 50.
REPEATED REASONING The mass of the particles that a river can transport is proportional to the sixth power of the speed of the river. A certain river normally flows at a speed of 1 meter per second. What must its speed be in order to transport particles that are twice as massive as usual? 10 times as massive? 100 times as massive?
Answer:
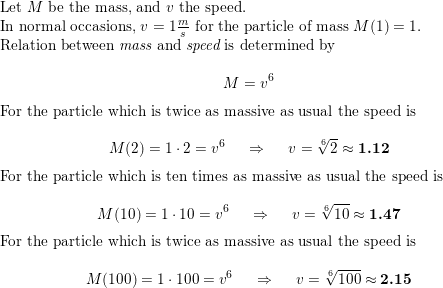
Maintaining Mathematical Proficiency
Simplify the expression. Write your answer using only positive exponents. (Skills Review Handbook)
Question 51.
5 • 54
Answer:
![]()
Question 52.
\(\frac{4^{2}}{4^{7}}\)
Answer:
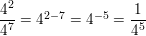
Question 53.
\(\left(z^{2}\right)^{-3}\)
Answer:
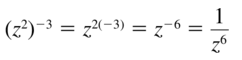
Question 54.
\(\left(\frac{3 x}{2}\right)^{4}\)
Answer:
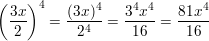
Write the number in standard form. (Skills Review Handbook)
Question 55.
5 × 103
Answer:
![]()
Question 56.
4 × 10−2
Answer:
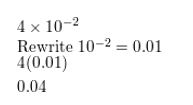
Question 57.
8.2 × 10−1
Answer:
![]()
Question 58.
6.93 × 106
Answer:
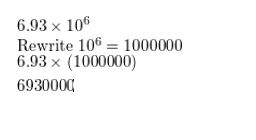
Lesson 5.2 Properties of Rational Exponents and Radicals
Essential Question
How can you use properties of exponents to simplify products and quotients of radicals?
EXPLORATION 1
Reviewing Properties of Exponents
Work with a partner. Let a and b be real numbers. Use the properties of exponents to complete each statement. Then match each completed statement with the property it illustrates.

Answer:
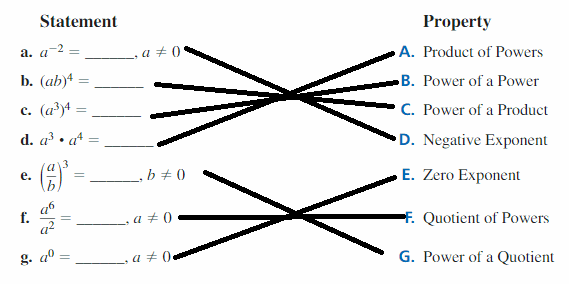
Explanation:
a. Negative Exponent: The negative exponent tells how many times we have to divide the base number.
b. Power of Product: The power of a product states that if a term is being to an exponent, you can distribute the power to each factor.
c. Power of a power: Multiply powers together when raising a power by another exponent.
d. Product of Powers: Add powers together when multiplying like bases.
e. Power of a Quotient: Distribute power to all values in a quotient.
f. Quotient of powers: Subtract powers when dividing the bases.
g. Zero Exponent: Any base raised to the power of 0, it gives the result as 1.
EXPLORATION 2
Simplifying Expressions with Rational Exponents
Work with a partner. Show that you can apply the properties of integer exponents to rational exponents by simplifying each expression. Use a calculator to check your answers.
a. \(5^{2 / 3}\) • \(5^{4 / 3}\)
b. \(3^{1 / 5}\) • \(3^{4 / 5}\)
c. \(\left(4^{2 / 3}\right)^{3}\)
d. \(\frac{\sqrt{98}}{\sqrt{2}}\)
e. \(\frac{\sqrt[4]{4}}{\sqrt[4]{1024}}\)
f. \(\frac{\sqrt[3]{625}}{\sqrt[3]{5}}\)
Answer:
a. \(5^{2 / 3}\) • \(5^{4 / 3}\) = 25
Explanation:
Given,
\(5^{2 / 3}\) • \(5^{4 / 3}\)
When bases are equal powers should be added.
52/3+4/3 = 6/3 = 2
5² = 25
b. \(3^{1 / 5}\) • \(3^{4 / 5}\) = 3
Explanation:
Given,
\(3^{1 / 5}\) • \(3^{4 / 5}\)
=31/5+4/5 = 5/5 = 1
=3
c. \(\left(4^{2 / 3}\right)^{3}\) = 16
Explanation:
Given,
\(\left(4^{2 / 3}\right)^{3}\)
42/3×3 = 2
=4²
= 16
d. \(\frac{\sqrt{98}}{\sqrt{2}}\) = 7
Explanation:
Given,
\(\frac{\sqrt{98}}{\sqrt{2}}\)
√(98/2) = √49 = 7
e. \(\frac{\sqrt[4]{4}}{\sqrt[4]{1024}}\) = 5
Explanation:
Given,
\(\frac{\sqrt[4]{4}}{\sqrt[4]{1024}}\)
\(\frac{\sqrt[4]}\)(4/1024) = \(\frac{\sqrt[4]}\)1/231
f. \(\frac{\sqrt[3]{625}}{\sqrt[3]{5}}\)
\(\frac{\sqrt[3]{625}}{\sqrt[3]{5}}\)
= 5
EXPLORATION 3
Simplifying Products and Quotients of Radicals
Work with a partner. Use the properties of exponents to write each expression as a single radical. Then evaluate each expression. Use a calculator to check your answers.

a. \(\sqrt{3}\) • \(\sqrt{12}\)
b. \(\sqrt[3]{5}\) • \(\sqrt[3]{25}\)
c. \(\sqrt[4]{27}\) • \(\sqrt[4]{3}\)
d. \(\frac{\sqrt{98}}{\sqrt{2}}\)
e. \(\frac{\sqrt[4]{4}}{\sqrt[4]{1024}}\)
f. \(\frac{\sqrt[3]{625}}{\sqrt[3]{5}}\)
Answer:
a.
Given,
\(\sqrt{3}\) • \(\sqrt{12}\)
\(\sqrt{a}\) • \(\sqrt{b}\) = \(\sqrt{ab}\)
= \(\sqrt{36}\)
= 6
b.
Given,
\(\sqrt[3]{5}\) • \(\sqrt[3]{25}\)
\(\sqrt{a}\) • \(\sqrt{b}\) = \(\sqrt{ab}\)
= \(\sqrt[3]{125}\)
= 5
c.
Given,
\(\sqrt[4]{27}\) • \(\sqrt[4]{3}\)
\(\sqrt{a}\) • \(\sqrt{b}\) = \(\sqrt{ab}\)
\(\sqrt[4]{81}\)
= 3
d.
Given,
\(\frac{\sqrt{98}}{\sqrt{2}}\)
√(98/2) = √49 = 7
e. \(\frac{\sqrt[4]{4}}{\sqrt[4]{1024}}\)
\(\frac{\sqrt[4]}\)(4/1024) = \(\frac{\sqrt[4]}\)1/231
f.
Given,
\(\frac{\sqrt[3]{625}}{\sqrt[3]{5}}\)
\(\frac{\sqrt[3]{625}}{\sqrt[3]{5}}\) = 5
Communicate Your Answer
Question 4.
How can you use properties of exponents to simplify products and quotients of radicals?
Answer: In order to rewrite radical expression applying first factor of expression which is under root making perfect power.
Property A: xm . xn = xm+n
Example:
52 . 52 = 54
Property B: am/bn = am-n
52/51 = 52-1= 5
Property C:
(am)n = amn
(52)1 = 52
Question 5.
Simplify each expression.
a. \(\sqrt{27}\) • \(\sqrt{6}\)
Answer:
Given,
\(\sqrt{27}\) • \(\sqrt{6}\)
\(\sqrt{162}\)
b. \(\frac{\sqrt[3]{240}}{\sqrt[3]{15}}\)
Answer:
Given,
\(\frac{\sqrt[3]{240}}{\sqrt[3]{15}}\)
\(\frac{\sqrt[3]{240/15}\) = 16
c. (\(5^{1 / 2}\) \(16^{1 / 4}\))²
Answer:
Given,
(\(5^{1 / 2}\) \(16^{1 / 4}\))²
(\(5^{1 / 2}\) \(16^{1 / 4}\))²
5 × \(16^{1 / 2}\)
5 × 4 = 20
5.2 Lesson
Monitoring Progress
Simplify the expression.
Question 1.
\(2^{3 / 4}\) • \(2^{1 / 2}\)
Answer:
Given,
\(2^{3 / 4}\) • \(2^{1 / 2}\)
xm . xn = xm+n
23/4+1/2 = 5/4
25/4
So, \(2^{3 / 4}\) • \(2^{1 / 2}\) = 25/4
Question 2.
\(\frac{3}{3^{1 / 4}}\)
Answer:
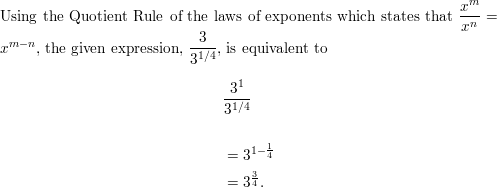
Question 3.
\(\left(\frac{20^{1 / 2}}{5^{1 / 2}}\right)^{3}\)
Answer:
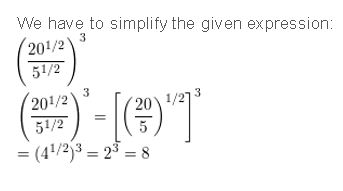
Question 4.
(\(5^{1 / 3}\) • \(7^{1 / 4}\))3
Answer:
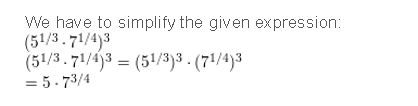
Simplify the expression
Question 5.
\(\sqrt[4]{27}\) • \(\sqrt[4]{3}\)
Answer:
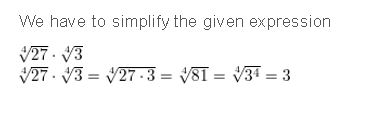
Question 6.
\(\frac{\sqrt[3]{250}}{\sqrt[3]{2}}\)
Answer:
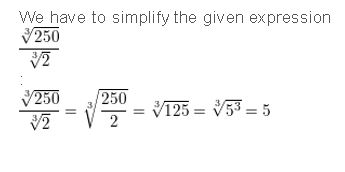
Question 7.
\(\sqrt[3]{104}\)
Answer:
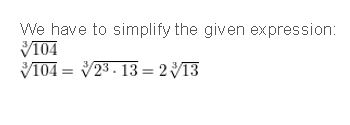
Question 8.
\(\sqrt[5]{\frac{3}{4}}\)
Answer:
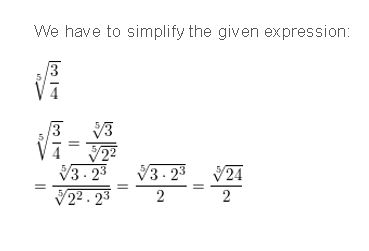
Question 9.
\(\frac{3}{6-\sqrt{2}}\)
Answer:
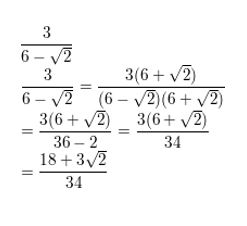
Question 10.
\(7 \sqrt[5]{12}\) – \(\sqrt[5]{12}\)
Answer:
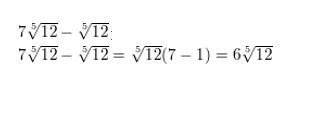
Question 11.
4(\(9^{2 / 3}\)) + (\(9^{2 / 3}\))
Answer:
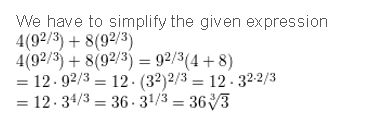
Question 12.
\(\sqrt[3]{5}\) + \(\sqrt[3]{40}\)
Answer:
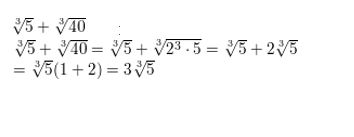
Simplify the expression. Assume all variables are positive.
Question 13.
\(\sqrt[3]{27 q^{9}}\)
Answer:
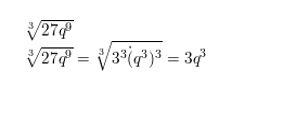
Question 14.
\(\sqrt[5]{\frac{x^{10}}{y^{5}}}\)
Answer:
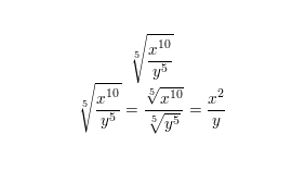
Question 15.
\(\frac{6 x y^{3 / 4}}{3 x^{1 / 2} y^{1 / 2}}\)
Answer:
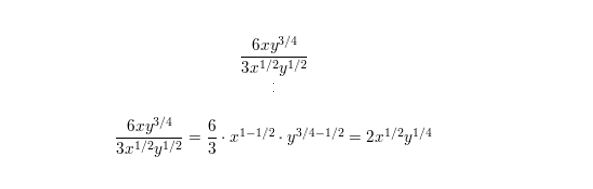
Question 16.
\(\sqrt{9} w^{5}\) – \(w \sqrt{w^{3}}\)
Answer:
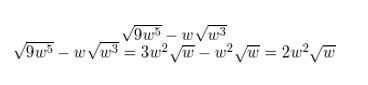
Properties of Rational Exponents and Radicals 5.2 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING How do you know when a radical expression is in simplest form?
Answer:

Question 2.
WHICH ONE DOESN’T BELONG? Which radical expression does not belong with the other three? Explain your reasoning.

Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 3–12, use the properties of rational exponents to simplify the expression.
Question 3.
\(\left(9^{2}\right)^{1 / 3}\)
Answer:
![]()
Question 4.
\(\left(12^{2}\right)^{1 / 4}\)
Answer:
Question 5.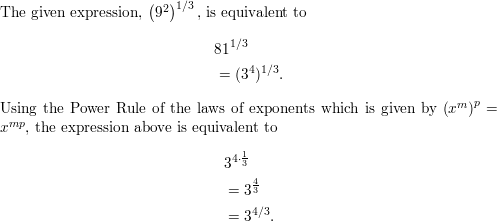
\(\frac{6}{6^{1 / 4}}\)
Answer:
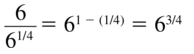
Question 6.
\(\frac{7}{7^{1 / 3}}\)
Answer:
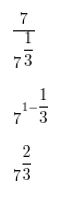
Question 7.
\(\left(\frac{8^{4}}{10^{4}}\right)^{-1 / 4}\)
Answer:
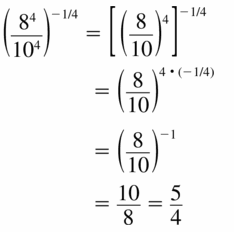
Question 8.
\(\left(\frac{9^{3}}{6^{3}}\right)^{-1 / 3}\)
Answer:
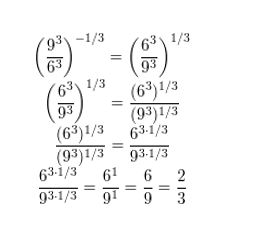
Question 9.
(\(3^{-2 / 3}\) • \(3^{1 / 3}\))-1
Answer:
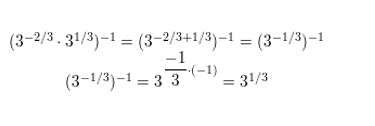
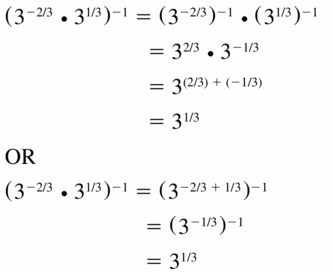
Question 10.
(\(5^{1 / 2}\) • \(5^{-3 / 2}\))-1/4
Answer:
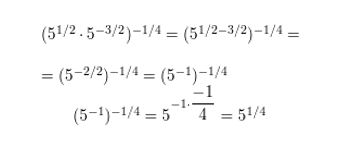
Question 11.
\(\frac{2^{2 / 3} \cdot 16^{2 / 3}}{4^{2 / 3}}\)
Answer:
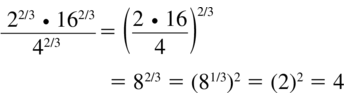
Question 12.
\(\frac{49^{3 / 8} \cdot 49^{7 / 8}}{7^{5 / 4}}\)
Answer:

In Exercises 13–20, use the properties of radicals to simplify the expression.
Question 13.
\(\sqrt{2}\) • \(\sqrt{72}\)
Answer:
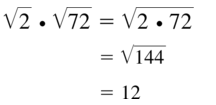
Question 14.
\(\sqrt[3]{16}\) • \(\sqrt[3]{32}\)
Answer:
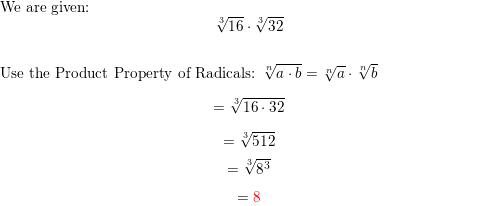
Question 15.
\(\sqrt[4]{6}\) • \(\sqrt[4]{8}\)
Answer:
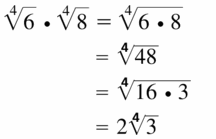
Question 16.
\(\sqrt[4]{8}\) • \(\sqrt[4]{8}\)
Answer:

Question 17.
\(\frac{\sqrt[5]{486}}{\sqrt[5]{2}}\)
Answer:
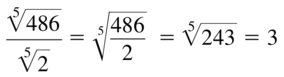
Question 18.
\(\frac{\sqrt{2}}{\sqrt{32}}\)
Answer:
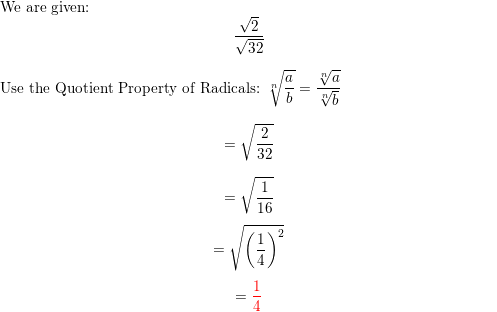
Question 19.
\(\frac{\sqrt[3]{6} \cdot \sqrt[3]{72}}{\sqrt[3]{2}}\)
Answer:
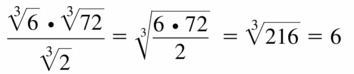
Question 20.
\(\frac{\sqrt[3]{3} \cdot \sqrt[3]{18}}{\sqrt[6]{2} \cdot \sqrt[6]{2}}\)
Answer:

In Exercises 21–28, write the expression in simplest form.
Question 21.
\(\sqrt[4]{567}\)
Answer:
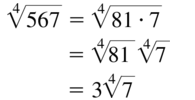
Question 22.
\(\sqrt[5]{288}\)
Answer:
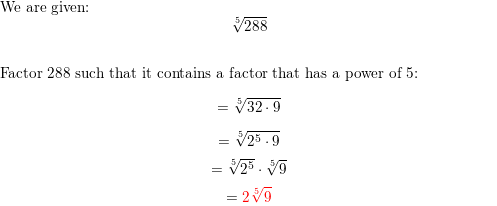
Question 23.
\(\frac{\sqrt[3]{5}}{\sqrt[3]{4}}\)
Answer:
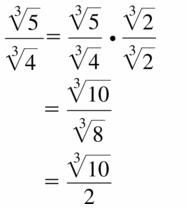
Question 24.
\(\frac{\sqrt[4]{4}}{\sqrt[4]{27}}\)
Answer:

Question 25.
\(\sqrt{\frac{3}{8}}\)
Answer:
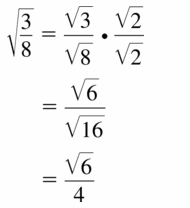
Question 26.
\(\sqrt[3]{\frac{7}{4}}\)
Answer:

Question 27.
\(\sqrt[3]{\frac{64}{49}}\)
Answer:
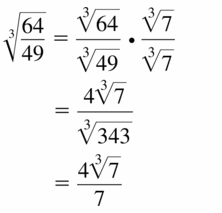
Question 28.
\(\sqrt[4]{\frac{1296}{25}}\)
Answer:

In Exercises 29–36, write the expression in simplest form.
Question 29.
\(\frac{1}{1+\sqrt{3}}\)
Answer:
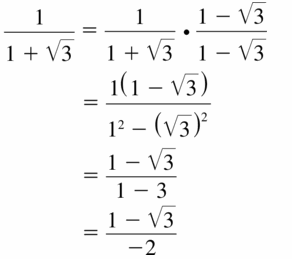
Question 30.
\(\frac{1}{2+\sqrt{5}}\)
Answer: √5 + 2
Explanation:
Given,
\(\frac{1}{2+\sqrt{5}}\) × \(\frac{2-\sqrt{5}{2-\sqrt{5}}\)
= \(\frac{2-\sqrt{5}{4-5}\)
= 2-√5/-1
= √5 + 2
Thus, \(\frac{1}{2+\sqrt{5}}\) = √5 + 2
Question 31.
\(\frac{5}{3-\sqrt{2}}\)
Answer:
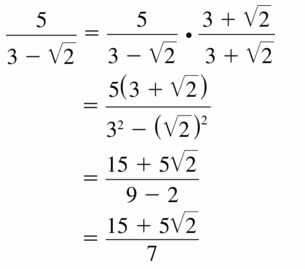
Question 32.
\(\frac{11}{9-\sqrt{6}}\)
Answer:
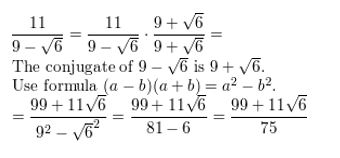
Question 33.
\(\frac{9}{\sqrt{3}+\sqrt{7}}\)
Answer:
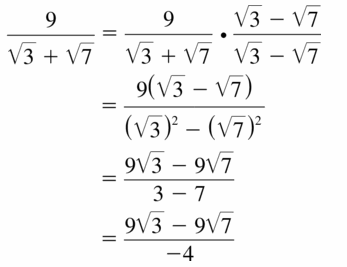
Question 34.
\(\frac{2}{\sqrt{8}+\sqrt{7}}\)
Answer:
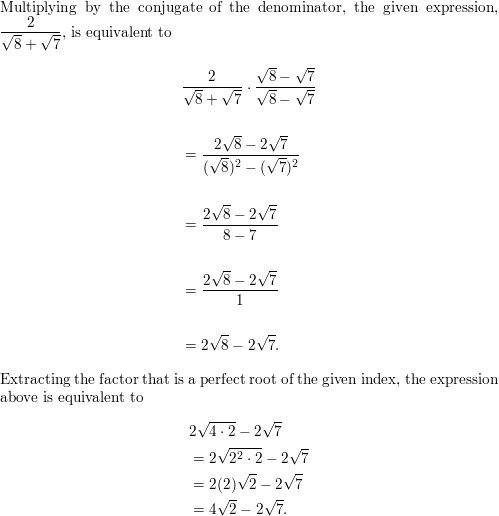
Question 35.
\(\frac{\sqrt{6}}{\sqrt{3}-\sqrt{5}}\)
Answer:
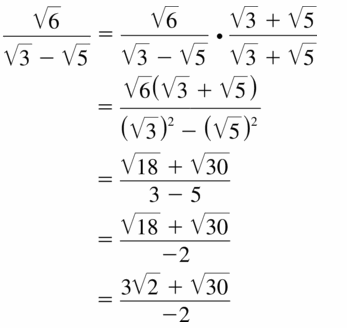
Question 36.
\(\frac{\sqrt{7}}{\sqrt{10}-\sqrt{2}}\)
Answer:
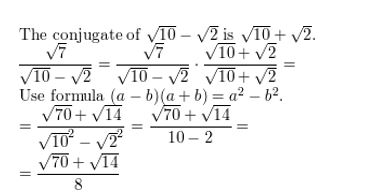
In Exercises 37–46, simplify the expression.
Question 37.
\(9 \sqrt[3]{11}\) + \(3 \sqrt[3]{11}\)
Answer:
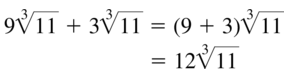
Question 38.
\(8 \sqrt[6]{5}\) – \(12 \sqrt[6]{5}\)
Answer:
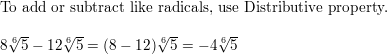
Question 39.
\(3\left(11^{1 / 4}\right)\) + \(9\left(11^{1 / 4}\right)\)
Answer:
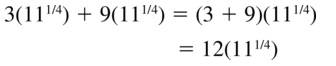
Question 40.
\(13\left(8^{3 / 4}\right)\) – \(4\left(8^{3 / 4}\right)\)
Answer:
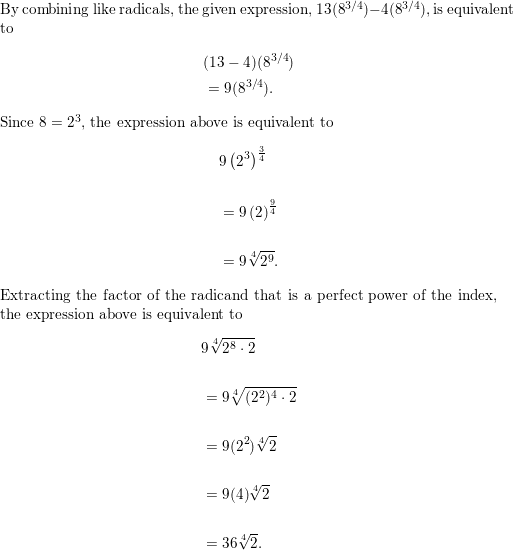
Question 41.
\(5 \sqrt{12}\) – \(19 \sqrt{3}\)
Answer:
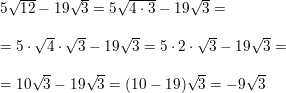
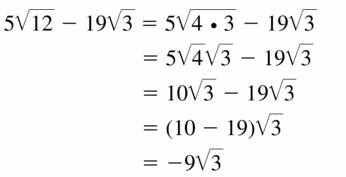
Question 42.
\(27 \sqrt{6}\) + \(7 \sqrt{150}\)
Answer: 34\(\sqrt{6}\)
Explanation:
Given,
\(27 \sqrt{6}\) + \(7 \sqrt{6.25}\)
= \(27 \sqrt{6}\) + \(35 \sqrt{6}\)
Take \( \sqrt{6}\) as common factor.
= \( \sqrt{6}\)(27+7)
= 34\(\sqrt{6}\)
So, \(27 \sqrt{6}\) + \(7 \sqrt{150}\) = 34\(\sqrt{6}\)
Question 43.
\(\sqrt[5]{224}\) + \(3 \sqrt[5]{7}\)
Answer:
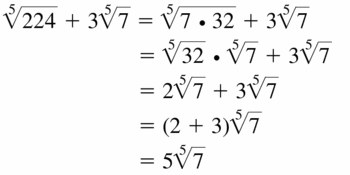
Question 44.
\(7 \sqrt[3]{2}\) – \(\sqrt[3]{128}\)
Answer:
Given,
\(7 \sqrt[3]{2}\) – \(\sqrt[3]{128}\)
\(\sqrt[3]{128}\) = 2\(\sqrt[3]{16}\)
\(7 \sqrt[3]{2}\) – 2\(\sqrt[3]{16}\)
So, \(7 \sqrt[3]{2}\) – \(\sqrt[3]{128}\) = \(7 \sqrt[3]{2}\) – 2\(\sqrt[3]{16}\)
Question 45.
\(5\left(24^{1 / 3}\right)\) – 4(\(\left(3^{1 / 3}\right)\))
Answer:
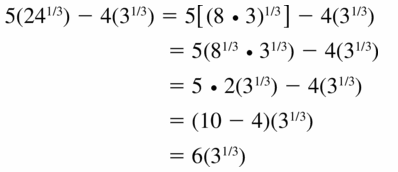
Question 46.
\(5^{1 / 4}\) + 6(\([405^{1 / 4}/latex])
Answer:
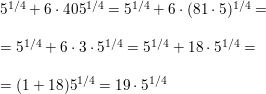
Question 47.
ERROR ANALYSIS Describe and correct the error in simplifying the expression.
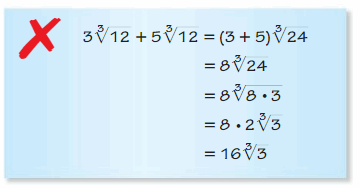
Answer:
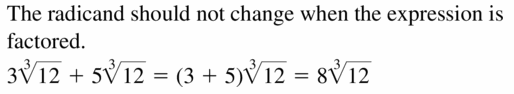
Question 48.
MULTIPLE REPRESENTATIONS Which radical expressions are like radicals?
A. [latex]\left(5^{2 / 9}\right)^{3 / 2}\)
B. \(\frac{5^{3}}{(\sqrt[3]{5})^{8}}\)
C. \(\sqrt[3]{625}\)
D. \(\sqrt[3]{5} 145\) – \(\sqrt[3]{875}\)
E. \(\sqrt[3]{5}\) + \(3 \sqrt[3]{5}\)
F. \(7 \sqrt[4]{80}\) – \(2 \sqrt[4]{405}\)
Answer:
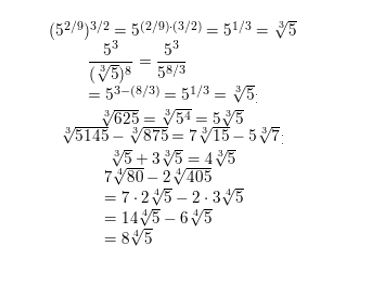
In Exercises 49–54, simplify the expression.
Question 49.
\(\sqrt[4]{81 y^{8}}\)
Answer:
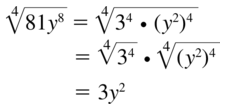
Question 50.
\(\sqrt[3]{64 r^{3} t^{6}}\)
Answer:
Given,
\(\sqrt[3]{64 r^{3} t^{6}}\)
= 4r\(\sqrt{t^{6}}\)
Question 51.
\(\sqrt[5]{\frac{m^{10}}{n^{5}}}\)
Answer:
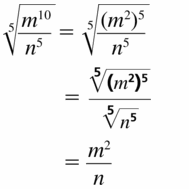
Question 52.
\(\sqrt[4]{\frac{k^{16}}{16 z^{4}}}\)
Answer:
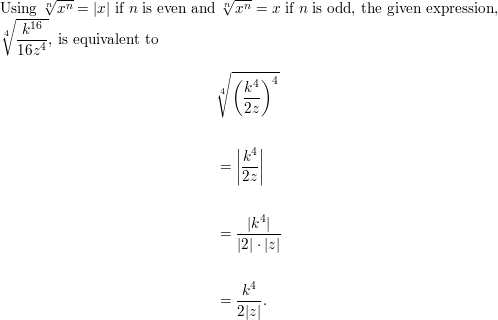
Question 53.
\(\sqrt[6]{\frac{g^{6} h}{h^{7}}}\)
Answer:
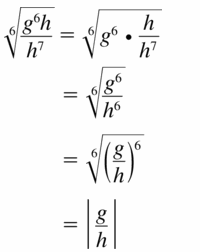
Question 54.
\(\sqr
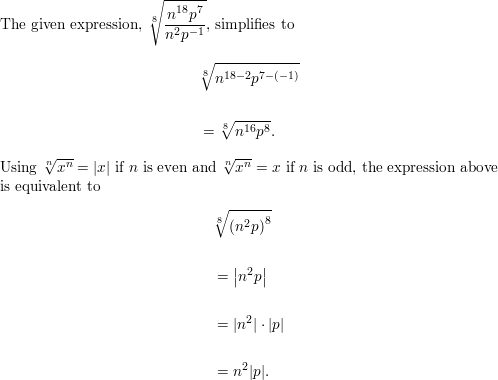
Question 55.
ERROR ANALYSIS Describe and correct the error in simplifying the expression.

Answer:
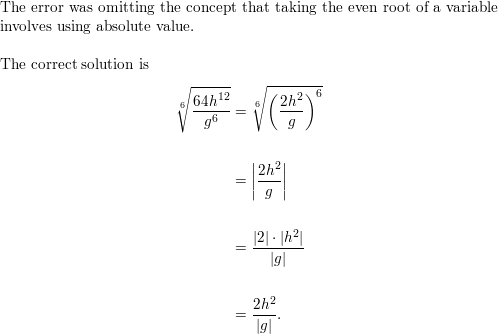

Question 56.
OPEN-ENDED Write two variable expressions involving radicals, one that needs absolute value in simplifying and one that does not need absolute value. Justify your answers.
Answer:
In Exercises 57–64, write the expression in simplest form. Assume all variables are positive.
Question 57.
[latex]\sqrt{81 a^{7} b^{12} c^{9}}\)
Answer:
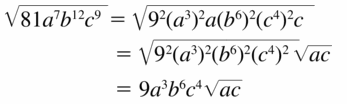
Question 58.
\(\sqrt[3]{125 r^{4} s^{9} t^{7}}\)
Answer:
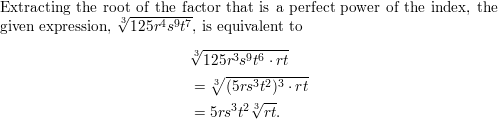
Question 59.
\(\sqrt[5]{\frac{160 m^{6}}{n^{7}}}\)
Answer:
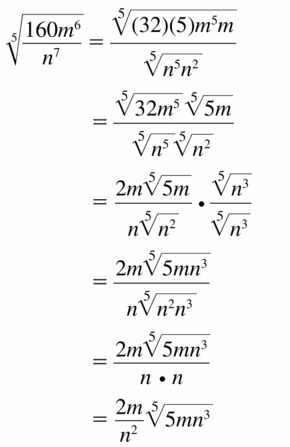
Question 60.
\(\sqrt[4]{\frac{405 x^{3} y^{3}}{5 x^{-1} y}}\)
Answer:
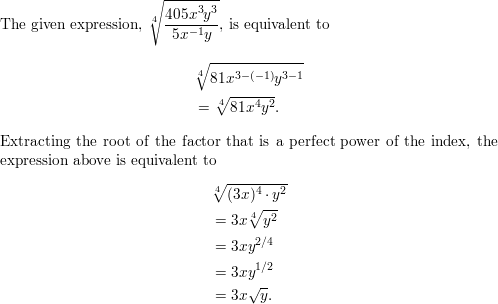
Question 61.
\(\frac{\sqrt[3]{w} \cdot \sqrt{w^{5}}}{\sqrt{25 w^{16}}}\)
Answer:
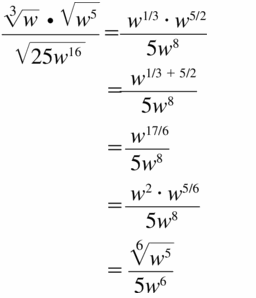
Question 62.
\(\frac{\sqrt[4]{v^{6}}}{\sqrt[7]{v^{5}}}\)
Answer:
Question 63.
\(\frac{18 w^{1 / 3} v^{5 / 4}}{27 w^{4 / 3} v^{1 / 2}}\)
Answer:
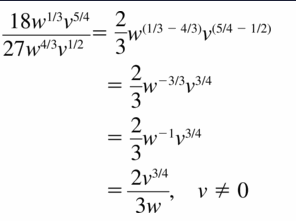
Question 64.
\(\frac{7 x^{-3 / 4} y^{5 / 2} z^{-2 / 3}}{56 x^{-1 / 2} y^{1 / 4}}\)
Answer:

In Exercises 65–70, perform the indicated operation. Assume all variables are positive.
Question 65.
\(12 \sqrt[3]{y}\) + \(9 \sqrt[3]{y}\)
Answer:
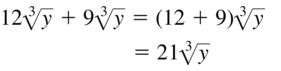
Question 66.
\(11 \sqrt{2 z}\) – \(5 \sqrt{2 z}\)
Answer:
Given,
\(11 \sqrt{2 z}\) – \(5 \sqrt{2 z}\)
Taking \( \sqrt{2 z}\) as common
(11 – 5)\( \sqrt{2 z}\)
6\( \sqrt{2 z}\)
So, \(11 \sqrt{2 z}\) – \(5 \sqrt{2 z}\) = 6\( \sqrt{2 z}\)
Question 67.
\(3 x^{7 / 2}\) – 5\(x^{7 / 2}\)
Answer:
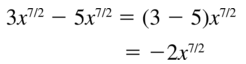
Question 68.
\(7 \sqrt[3]{m^{7}}\) + \(3 m^{7 / 3}\)
Answer:
Given,
\(7 \sqrt[3]{m^{7}}\) + \(3 m^{7 / 3}\)
\(7 m^{7 / 3}\) + \(3 m^{7 / 3}\)
Taking \(m^{7 / 3}\) as common.
(7 + 3)\(m^{7 / 3}\)
10\(m^{7 / 3}\)
So, \(7 \sqrt[3]{m^{7}}\) + \(3 m^{7 / 3}\) = 10\(m^{7 / 3}\)
Question 69.
\(\sqrt[4]{16 w^{10}}\) + \(2 w \sqrt[4]{w^{6}}\)
Answer:
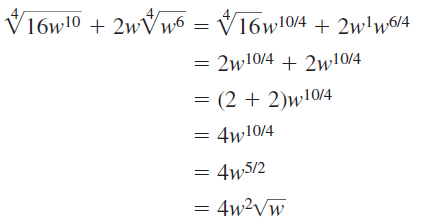
Question 70.
(p1/2 • p1/4) – \(\sqrt[4]{16 p^{3}}\)
Answer:
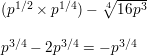
MATHEMATICAL CONNECTIONS In Exercises 71 and 72, find simplified expressions for the perimeter and area of the given figure.
Question 71.
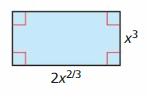
Answer:
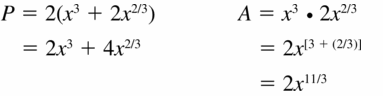
Question 72
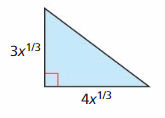
Answer:

Question 73.
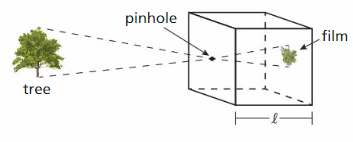
MODELING WITH MATHEMATICS The optimum diameter d (in millimeters) of the pinhole in a pinhole camera can be modeled by d = 1.9[(5.5 × 10−4)ℓ]1/2, where ℓ is the length (in millimeters) of the camera box. Find the optimum pinhole diameter for a camera box with a length of 10 centimeters.
Answer:

Question 74.
MODELING WITH MATHEMATICS The surface area S(in square centimeters) of a mammal can be modeled by S = km2/3, where m is the mass (in grams) of the mammal and k is a constant. The table shows the values of k for different mammals.

a. Find the surface area of a bat whose mass is 32 grams.
b. Find the surface area of a rabbit whose mass is 3.4 kilograms (3.4 × 103 grams).
c. Find the surface area of a human whose mass is 59 kilograms.
Answer:

Question 75.
MAKING AN ARGUMENT Your friend claims it is not possible to simplify the expression 7\(\sqrt{11}\) − 9 \(\sqrt{44}\) because it does not contain like radicals. Is your friend correct? Explain your reasoning.
Answer:
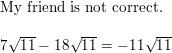

Question 76.
PROBLEM SOLVING The apparent magnitude of a star is a number that indicates how faint the star is in relation to other stars. The expression f(x) = \(\frac{2.512^{m_{1}}}{2.512^{m_{2}}}\) tells how many times fainter a star with apparent magnitude m1 is than a star with apparent magnitude m2.
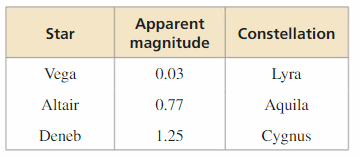
a. How many times fainter is Altair than Vega?
b. How many times fainter is Deneb than Altair?
c. How many times fainter is Deneb than Vega?
Answer:

Question 77.
CRITICAL THINKING Find a radical expression for the perimeter of the triangle inscribed in the square shown. Simplify the expression.
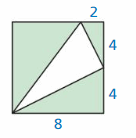
Answer:
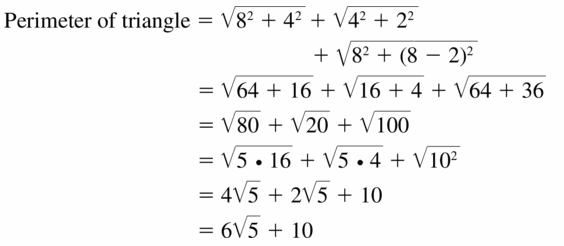
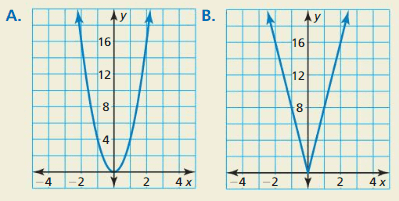
Question 78.
HOW DO YOU SEE IT? Without finding points, match the functions f(x) = \(\sqrt{64 x^{2}}\) and g(x) = \(\sqrt[3]{64 x^{6}}\) with their graphs. Explain your reasoning.
Answer:
Question 79.
REWRITING A FORMULA You have filled two round balloons with water. One balloon contains twice as much water as the other balloon.
a. Solve the formula for the volume of a sphere, V = \(\frac{4}{3}\)πr3, for r.
b. Substitute the expression for r from part (a) into the formula for the surface area of a sphere, S = 4πr2. Simplify to show that S = (4π)1/3(3V)2/3.
c. Compare the surface areas of the two water balloons using the formula in part (b).
Answer:
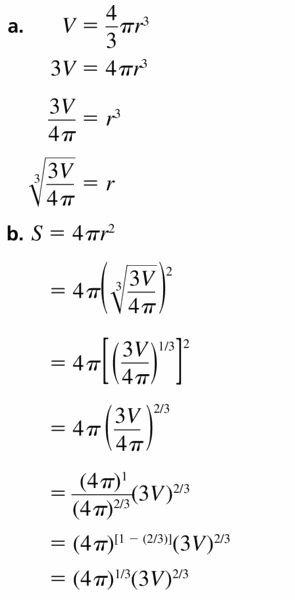

Question 80.
THOUGHT PROVOKING Determine whether the expressions (x2)1/6 and (x1/6)2 are equivalent for all values of x.
Answer:

Question 81.
DRAWING CONCLUSIONS Substitute different combinations of odd and even positive integers for m and n in the expression \(\sqrt[n]{x^{m}}\). When you cannot assume x is positive, explain when absolute value is needed in simplifying the expression.
Answer:

Maintaining Mathematical Proficiency
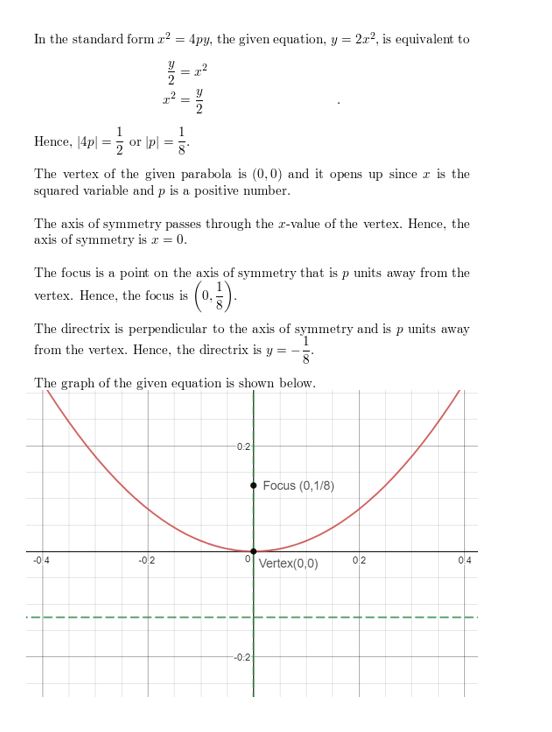
Identify the focus, directrix, and axis of symmetry of the parabola. Then graph the equation. (Section 2.3)
Question 82.
y = 2x2
Answer:
Question 83.
y2 = −x
Answer:

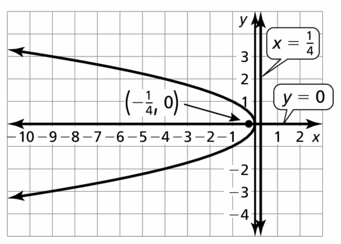
Question 84.
y2 = 4x
Answer:

Write a rule for g. Describe the graph of g as a transformation of the graph of f. (Section 4.7)
Question 85.
f(x) = x4 − 3x2 − 2x, g(x) = −f(x)
Answer:
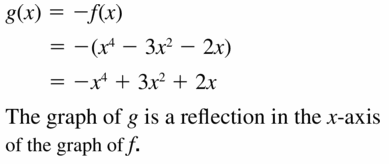
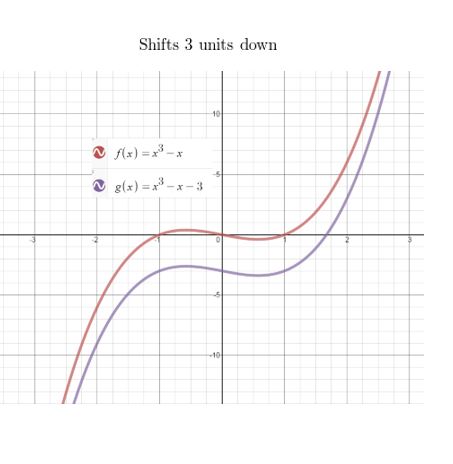
Question 86.
f(x) = x3 − x, g(x) = f(x) − 3
Answer:
Question 87.
f(x) = x3 − 4, g(x) = f(x − 2)
Answer:

Question 88.
f(x) = x4 + 2x3 − 4x2, g(x) = f(2x)
Answer:
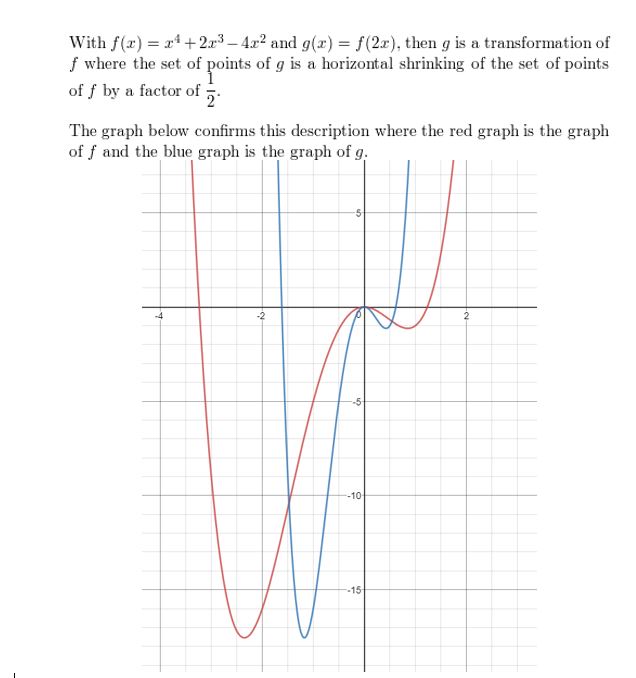
Lesson 5.3 Graphing Radical Functions
Essential Question
How can you identify the domain and range of a radical function?
EXPLORATION 1
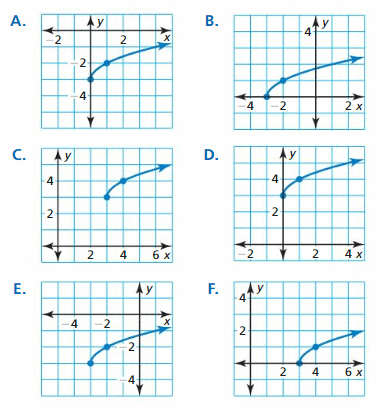
Identifying Graphs of Radical Functions
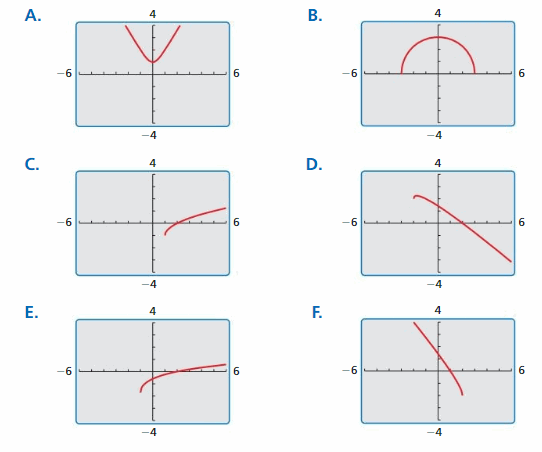
Work with a partner. Match each function with its graph. Explain your reasoning. Then identify the domain and range of each function.
a. f(x) = \(\sqrt{x}\)
b. f(x) = \(\sqrt[3]{x}\)
c. f(x) = \(\sqrt[4]{x}\)
d. f(x) = \(\sqrt[5]{x}\)
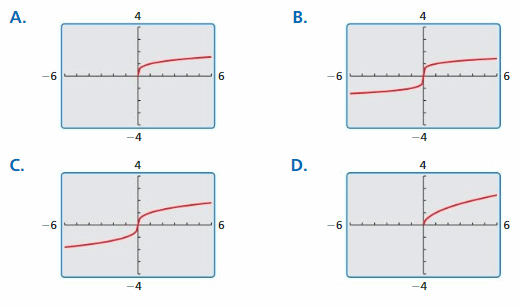
Answer:
a.
f(x) = \(\sqrt{x}\) suits with graph D.
So, D is the correct answer.
b. f(x) = \(\sqrt[3]{x}\) suits with graph C.
So, Graph C is the correct answer.
c. f(x) = \(\sqrt[4]{x}\) suits with graph A.
So, Graph A is the correct answer.
d. f(x) = \(\sqrt[5]{x}\) suits with graph B.
So, Graph B is the correct answer.
EXPLORATION 2
Identifying Graphs of Transformations
Work with a partner. Match each transformation of f(x) = \(\sqrt{x}\) with its graph. Explain your reasoning. Then identify the domain and range of each function.
a. g(x) = \(\sqrt{x+2}\)
b. g(x) = \(\sqrt{x-2}\)
c. g(x) = \(\sqrt{x}+2-2\)
d. g(x) = −\(\sqrt{x+2}\)
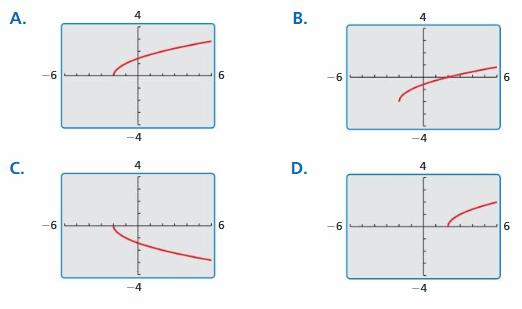
Communicate Your Answer
Question 3.
How can you identify the domain and range of a radical function?
Answer:
- The domain and range of a radical function f(x) having an even order are all positive numbers and zero as the radicand takes only positive values.
- The domain and range of a radical function f(x) having an odd order are all real numbers as radicand can take the value of any real number. f(x) = √x.

Question 4.
Use the results of Exploration 1 to describe how the domain and range of a radical function are related to the index of the radical.
Answer:
- The functions \(\sqrt{x}\) and \(\sqrt[4]{x}\) have the domain and the range as [0, ∞)
- The functions \(\sqrt[3]{x}\) and \(\sqrt[5]{x}\) have the domain and the range as (-∞, ∞)
- If the index of the given radical is odd, its domain and range will not have any restriction. Whereas if it is even, they will have restrictions.
5.3 Lesson
Monitoring Progress
Question 1.
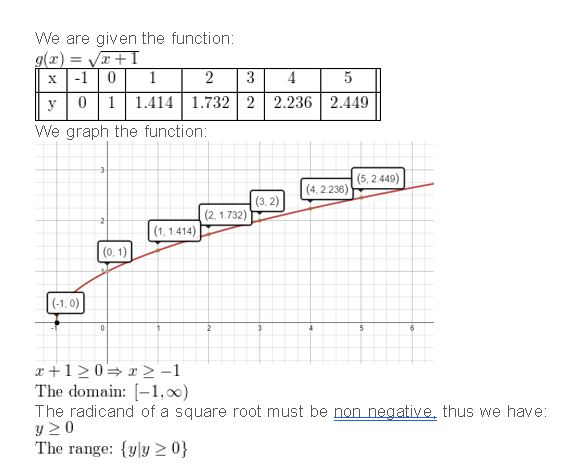
Graph g(x) = \(\sqrt{x+1}\). Identify the domain and range of the function.
Answer:
Question 2.
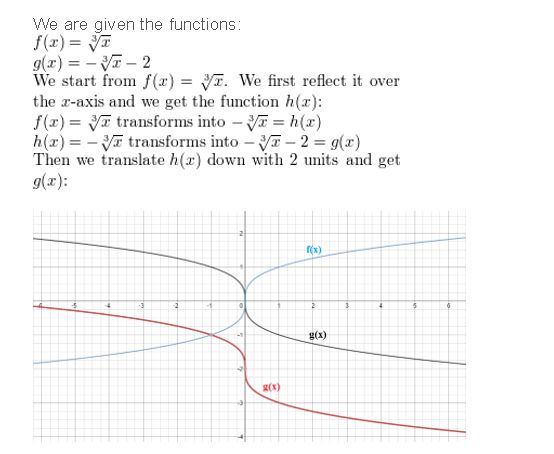
Describe the transformation of f(x) = \(\sqrt[3]{x}\) represented by g(x) = −\(\sqrt[3]{x}\) − 2. Then graph each function.
Answer:
Question 3.
WHAT IF? In Example 3, the function N(d ) = 2.4 • E(d) approximates the number of seconds it takes a dropped object to fall d feet on the Moon. Write a rule for N. How long does it take a dropped object to fall 25 feet on the Moon?
Answer:
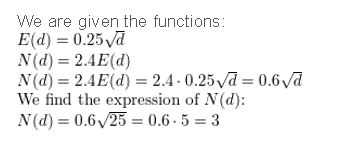
Question 4.
In Example 4, is the transformed function the same when you perform the translation followed by the horizontal shrink? Explain your reasoning.
Answer:
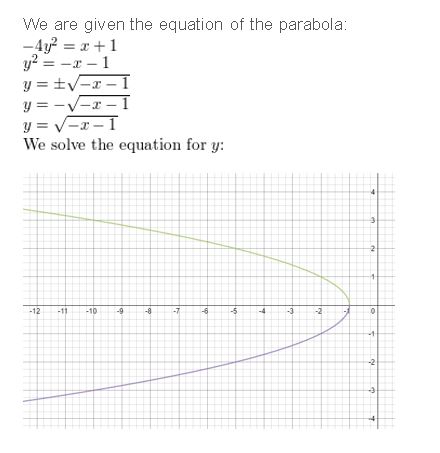
Question 5.
Use a graphing calculator to graph −4y2 = x + 1. Identify the vertex and the direction that the parabola opens.
Answer:
Question 6.
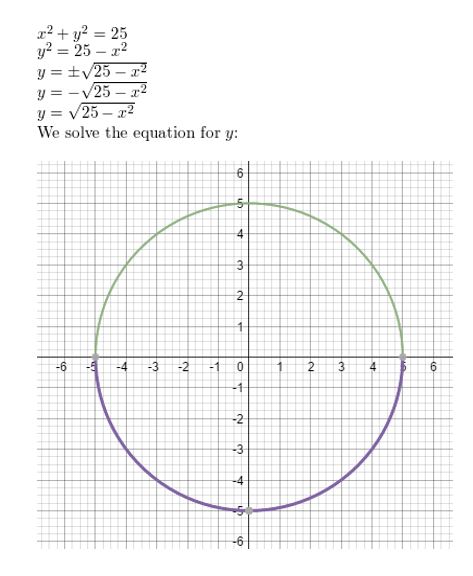
Use a graphing calculator to graph x2 + y2 = 25. Identify the radius and the intercepts.
Answer:
Graphing Radical Functions 5.3 Exercises
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE Square root functions and cube root functions are examples of __________ functions.
Answer:
Square root functions and cube root functions are examples of radical functions.
Question 2.
COMPLETE THE SENTENCE When graphing y = a\(\sqrt[3]{x-h}\) + k, translate the graph of y = a\(\sqrt[3]{x}\)h units __________ and k units __________.
Answer:
Square root functions and cube root functions are examples of radical functions
Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, match the function with its graph.
Question 3.
f(x) = \(\sqrt{x}+3\)
Answer:
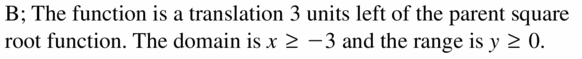
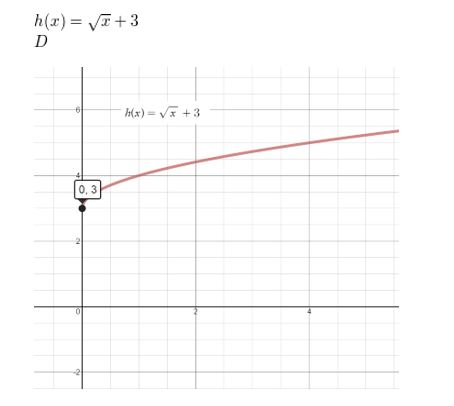
Question 4.
h(x) = \(\sqrt{x}\) + 3
Answer:
Question 5.
f(x) = \(\sqrt{x-3}\)
Answer:

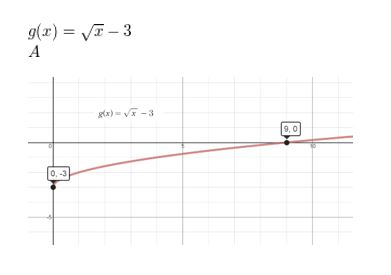
Question 6.
g(x) = \(\sqrt{x}\) − 3
Answer:
Question 7.
h(x) = \(\sqrt{x+3}\) − 3
Answer:

Question 8.
f(x) = \(\sqrt{x-3}\) + 3
Answer:
In Exercises 9–18, graph the function. Identify the domain and range of the function.
Question 9.
h(x) = \(\sqrt{x}\) + 4
Answer:
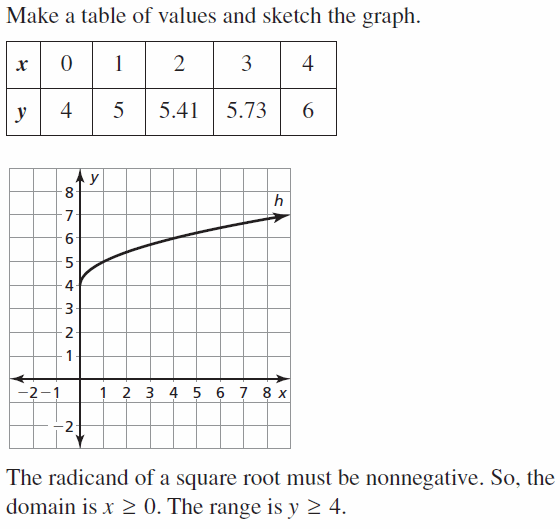
Question 10.
g(x) = \(\sqrt{x}\) − 5
Answer:
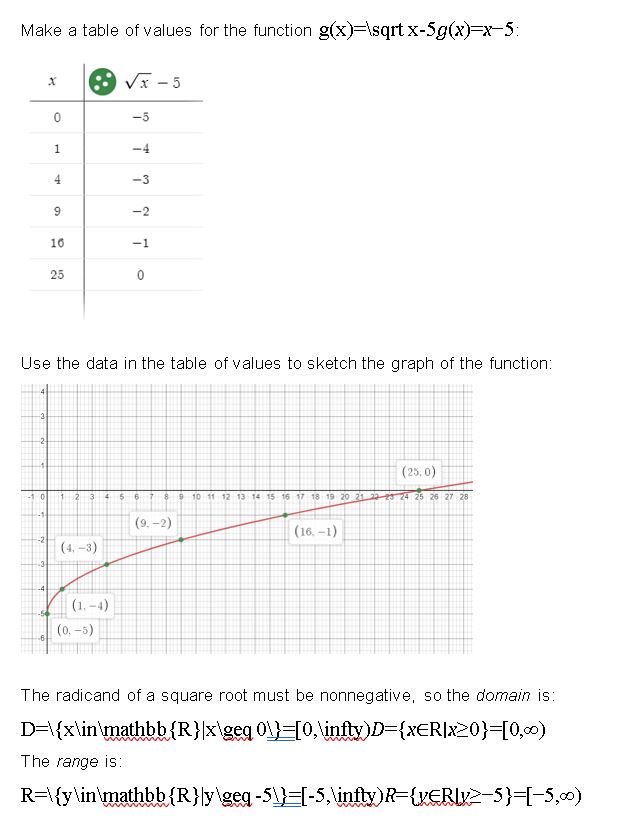
Question 11.
g(x) = − \(\sqrt[3]{2 x}\)
Answer:
Question 12.
f(x) = \(\sqrt[3]{-5 x}\)
Answer:
Question 13.
g(x) = \(\frac{1}{5} \sqrt{x}-3\)
Answer:
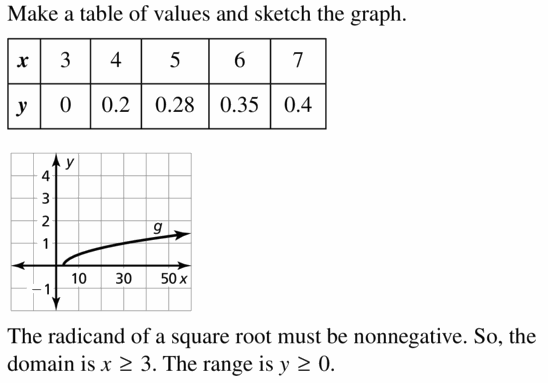
Question 14.
f(x) = \(\frac{1}{2} \sqrt[3]{x}+6\)
Answer:
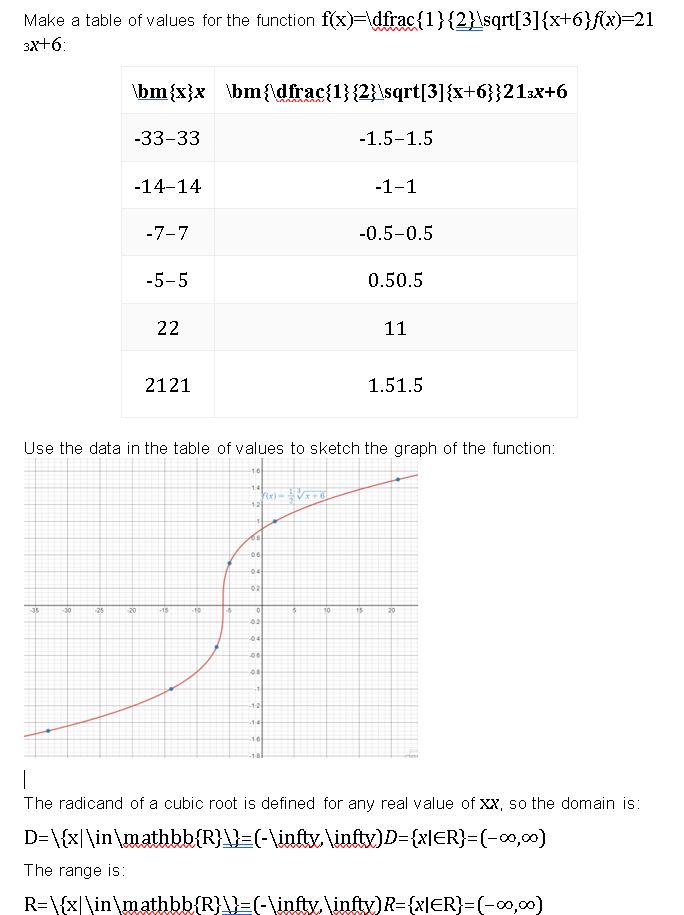
Question 15.
f(x) = \((6 x)^{1 / 2}\) + 3
Answer:
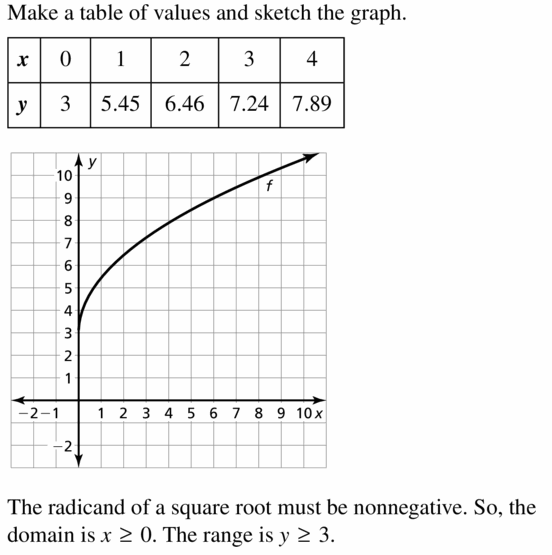
Question 16.
g(x) = −3(x + 1)1/3
Answer:
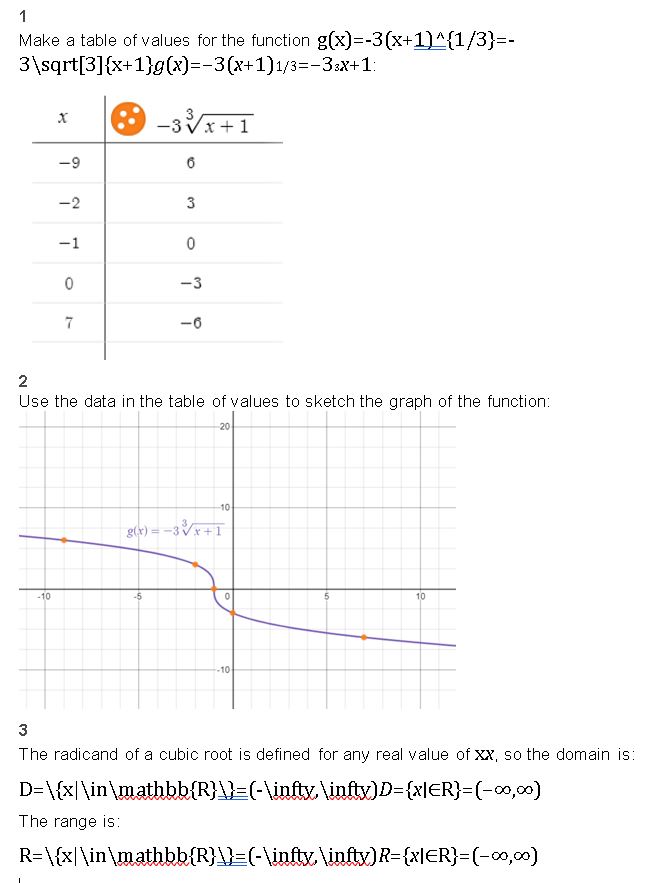
Question 17.
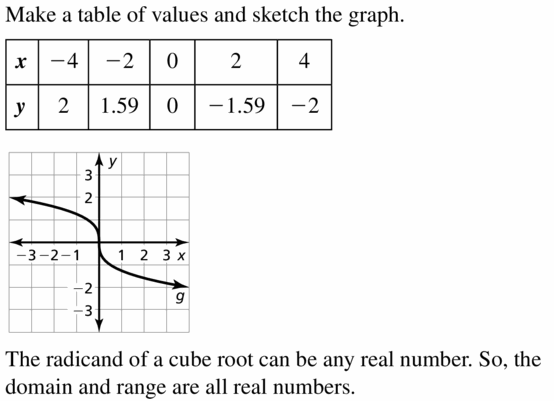
h(x) = −\(\sqrt[4]{x}\)
Answer:
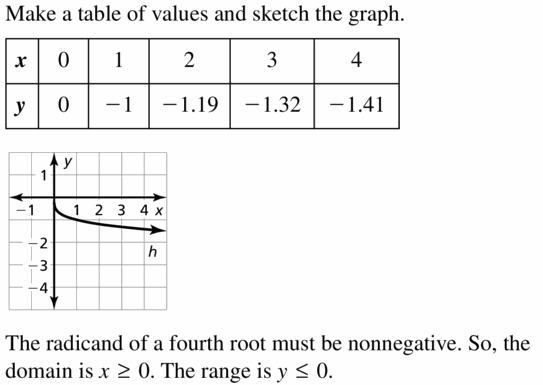
Question 18.
h(x) = \(\sqrt[5]{2 x}\)
Answer:
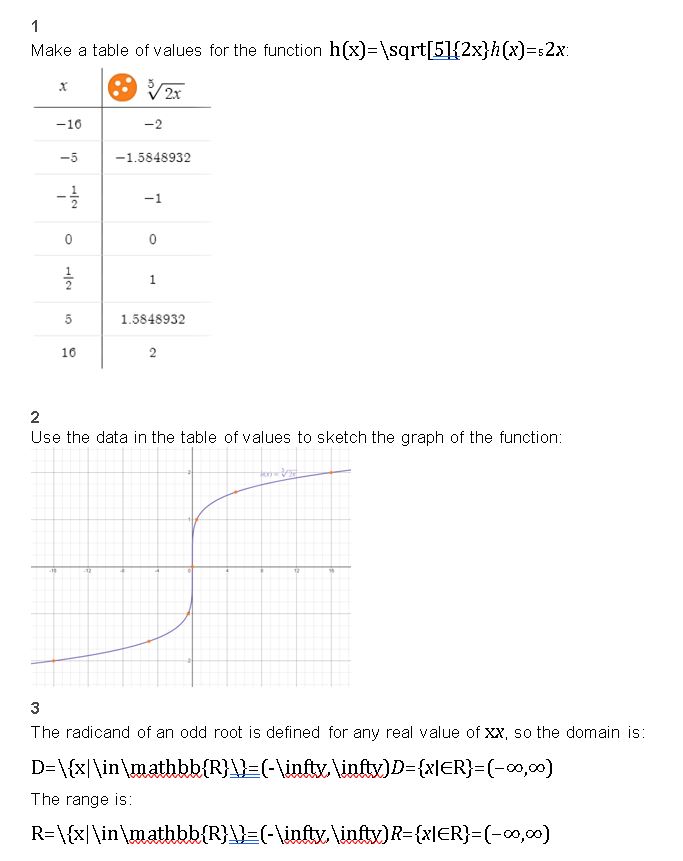
In Exercises 19–26, describe the transformation of f represented by g. Then graph each function.
Question 19.
f(x) = \(\sqrt{x}\), g(x) = \(\sqrt{x+1}\) + 8
Answer:
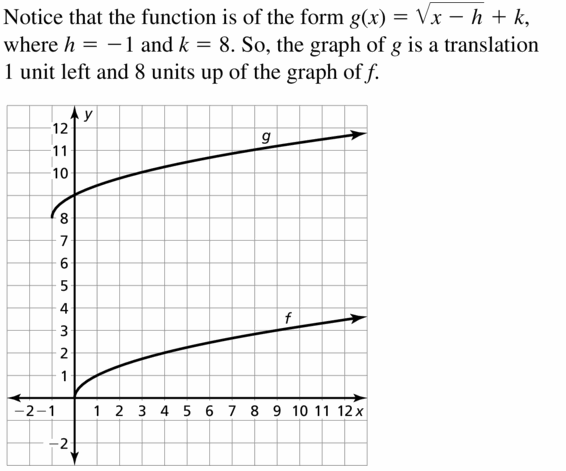
Question 20.
f(x) = \(\sqrt{x}\), g(x) = 2\(\sqrt{x-1}\)
Answer:
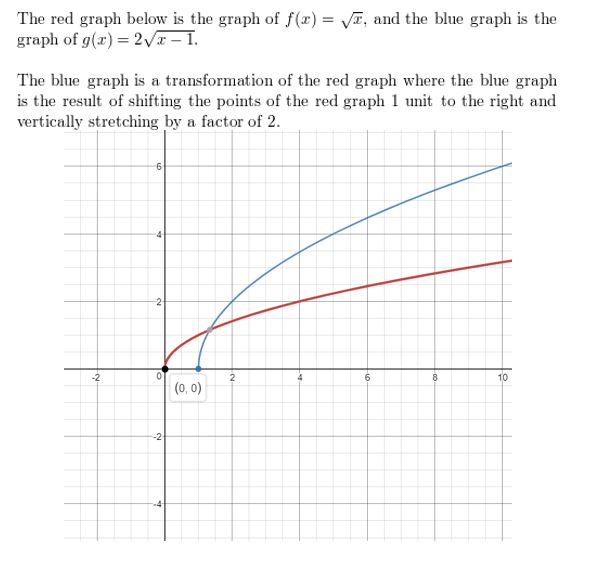
Question 21.
f(x) = \(\sqrt[3]{x}\), g(x) = −\(\sqrt[3]{x}\) − 1
Answer:
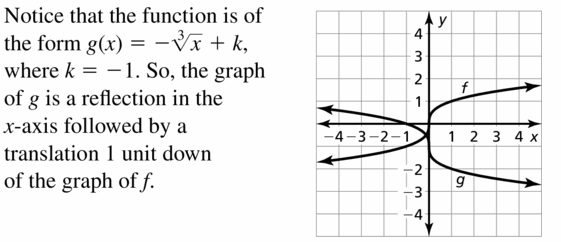
Question 22.
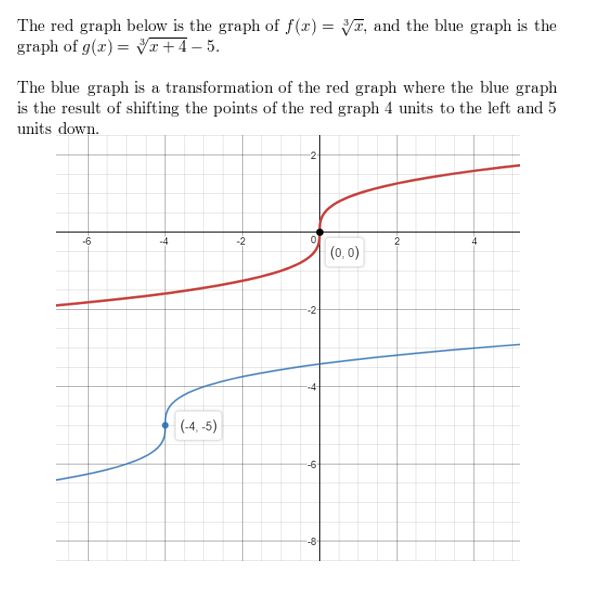
f(x) = \(\sqrt[3]{x}\), g(x) = \(\sqrt[3]{x+4}\) − 5
Answer:
Question 23.
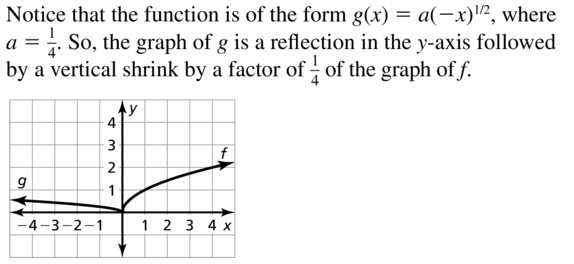
f(x) = \(x^{1 / 2}\), g(x) = \(\frac{1}{4}(-x)^{1 / 2}\)
Answer:
Question 24.
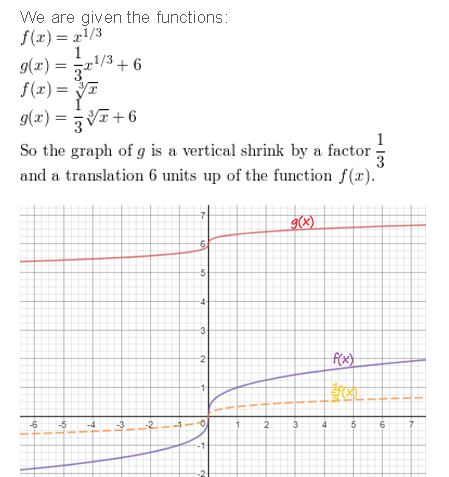
f(x) = \(x^{1 / 3}\), g(x) = \(\frac{1}{3} x^{1 / 3}\) + 6
Answer:
Question 25.
f(x) = \(\sqrt[4]{x}\), g(x) = \(2 \sqrt[4]{x+5}\) − 4
Answer:
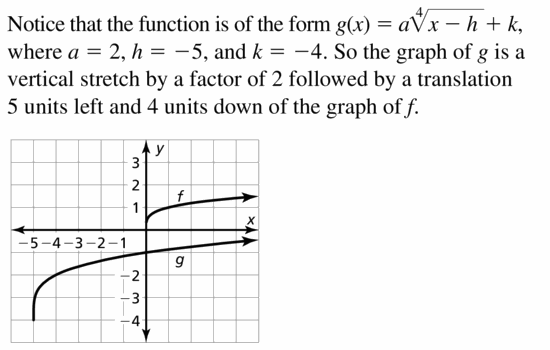
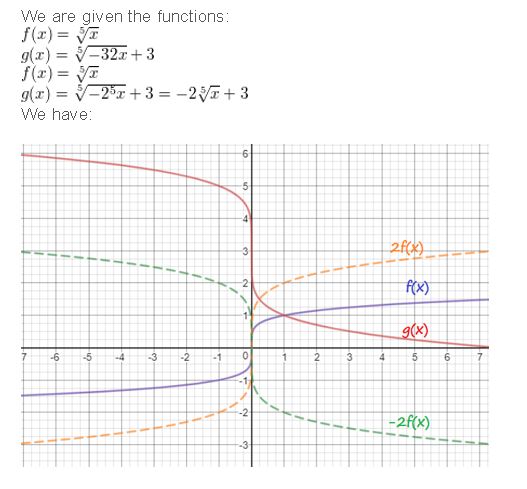
Question 26.
f(x) = \(\sqrt[5]{x}\), g(x) = \(\sqrt[5]{-32 x}\) + 3
Answer:
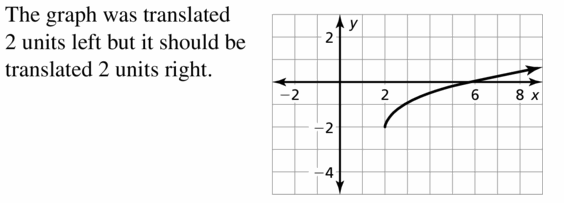
Question 27.
ERROR ANALYSIS Describe and correct the error in graphing f(x) = \(\sqrt{x-2}\) − 2.
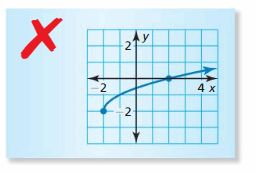
Answer:
Question 28.
ERROR ANALYSIS Describe and correct the error in describing the transformation of the parent square root function represented by g(x) = \(\sqrt{\frac{1}{2} x}\) + 3.

Answer:
The graph of g is a horizontal stretch by a factor of 2 and translation 3 units up of the parent square root function.
USING TOOLS In Exercises 29–34, use a graphing calculator to graph the function. Then identify the domain and range of the function.
Question 29.
g(x) = \(\sqrt{x^{2}+x}\)
Answer:
Question 30.
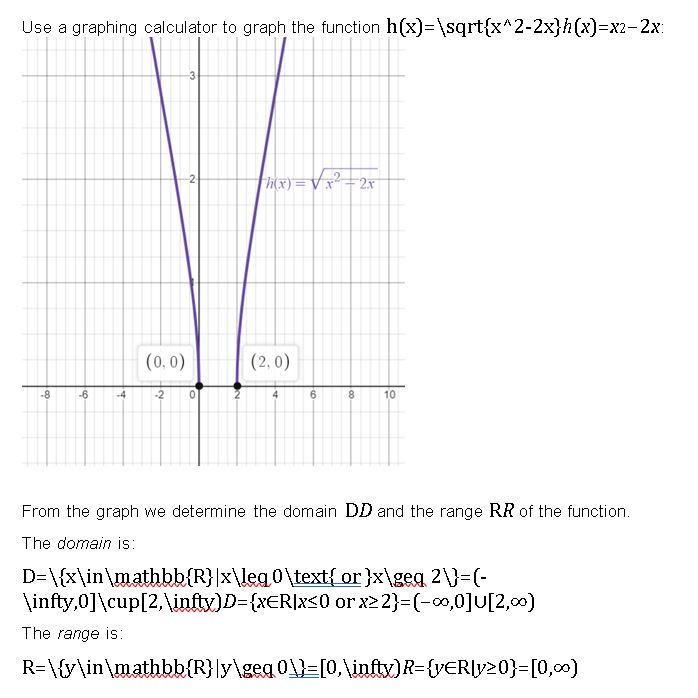
h(x) = \(\sqrt{x^{2}-2 x}\)
Answer:
Question 31.
f(x) = \(\sqrt[3]{x^{2}+x}\)
Answer:

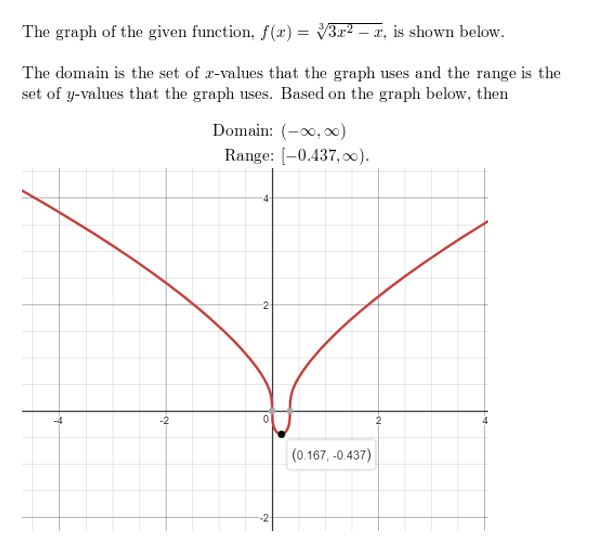
Question 32.
f(x) = \(\sqrt[3]{3 x^{2}-x}\)
Answer:
Question 33.
f(x) = \(\sqrt{2 x^{2}+x+1}\)
Answer:

Question 34.
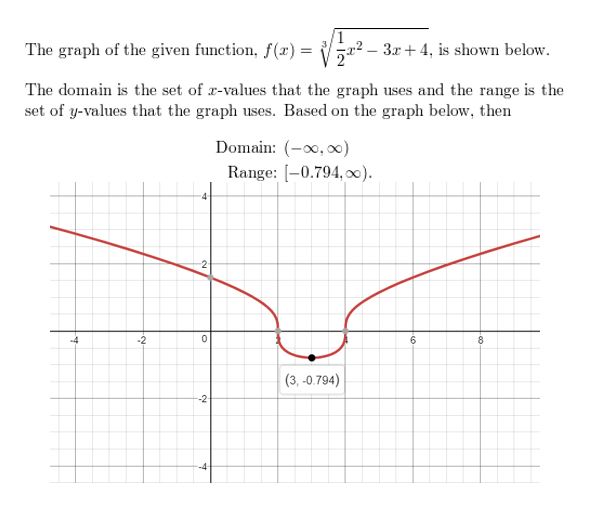
h(x) = \(\sqrt[3]{\frac{1}{2} x^{2}-3 x+4}\)
Answer:
ABSTRACT REASONING In Exercises 35–38, complete the statement with sometimes, always, or never.
Question 35.
The domain of the function y = a\(\sqrt{x}\) is ______ x ≥ 0.
Answer: The domain of the function y = a\(\sqrt{x}\) is always x ≥ 0.
Question 36.
The range of the function y = a\(\sqrt{x}\) is ______ y ≥ 0.
Answer: The range of the function y = a\(\sqrt{x}\) is sometimes y ≥ 0.
Question 37.
The domain and range of the function y = \(\sqrt[3]{x-h}\) + k are ________ all real numbers.
Answer: The domain and range of the function y = \(\sqrt[3]{x-h}\) + k are always all real numbers.
Question 38.
The domain of the function y = a\(\sqrt{-x}\) + k is ________ x ≥ 0.
Answer: The domain of the function y = a\(\sqrt{-x}\) + k is never x ≥ 0.
Question 39.
PROBLEM SOLVING The distance (in miles) a pilot can see to the horizon can be approximated by E(n) = 1.22\(\sqrt{n}\), where n is the plane’s altitude (in feet above sea level) on Earth. The function M(n) = 0.75E(n) approximates the distance a pilot can see to the horizon n feet above the surface of Mars. Write a rule for M. What is the distance a pilot can see to the horizon from an altitude of 10,000 feet above Mars?
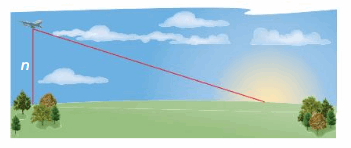
Answer:
Question 40.
MODELING WITH MATHEMATICS The speed (in knots) of sound waves in air can be modeled by v(K) = 643.855\(\sqrt{\frac{K}{273.15}}\) where K is the air temperature (in kelvin). The speed (in meters per second) of sound waves in air can be modeled by s(K) = \(\frac{v(K)}{1.944}\). Write a rule for s. What is the speed (in meters per second) of sound waves when the air temperature is 305 kelvin?
Answer:

In Exercises 41–44, write a rule for g described by the transformations of the graph of f.
Question 41.
Let g be a vertical stretch by a factor of 2, followed by a translation 2 units up of the graph of f(x) = \(\sqrt{x}\) + 3.
Answer:

Question 42.
Let g be a reflection in the y-axis, followed by a translation 1 unit right of the graph of f(x) = \(2 \sqrt[3]{x-1}\).
Answer:
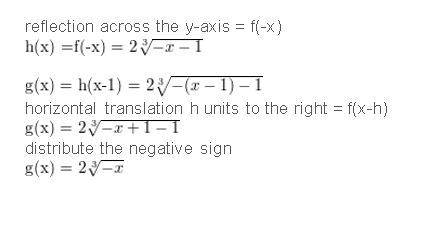
Question 43.
Let g be a horizontal shrink by a factor of \(\frac{2}{3}\), followed by a translation 4 units left of the graph of f(x) = \(\sqrt{6 x}\).
Answer:

Question 44.
Let g be a translation 1 unit down and 5 units right, followed by a reflection in the x-axis of the graph of f(x) = −\(-\frac{1}{2} \sqrt[4]{x}+\frac{3}{2}\)
Answer:

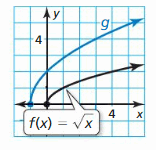
In Exercises 45 and 46, write a rule for g.
Question 45.
Answer:

Question 46.
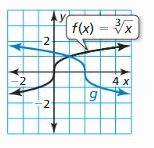
Answer:
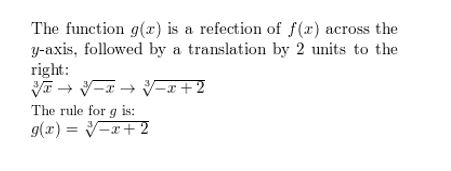
In Exercises 47–50, write a rule for g that represents the indicated transformation of the graph of f.
Question 47.
f(x) = 2\(\sqrt{x}\), g(x) = f(x + 3)
Answer:

Question 48.
f(x) = \(\frac{1}{3} \sqrt{x-1}\), g(x) = −f(x) + 9
Answer:
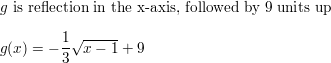
Question 49.
f(x) = −\(\sqrt{x^{2}-2}\), g(x) = −2f(x + 5)
Answer:

Question 50.
f(x) = \(\sqrt[3]{x^{2}+10 x}\), g(x) =\(\frac{1}{4}\)f(−x) + 6
Answer:
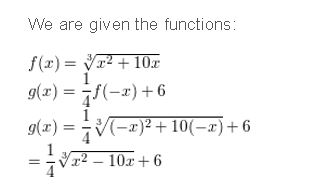
In Exercises 51–56, use a graphing calculator to graph the equation of the parabola. Identify the vertex and the direction that the parabola opens.
Question 51.
\(\frac{1}{4}\)y2 = x
Answer:
Question 52.
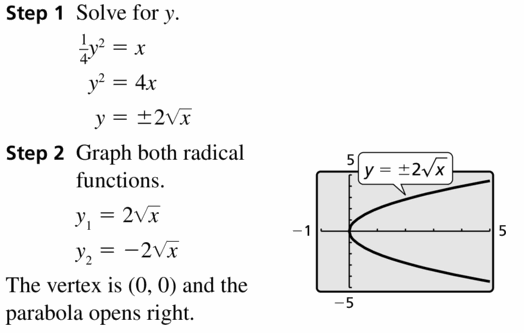
3y2 = x
Answer:
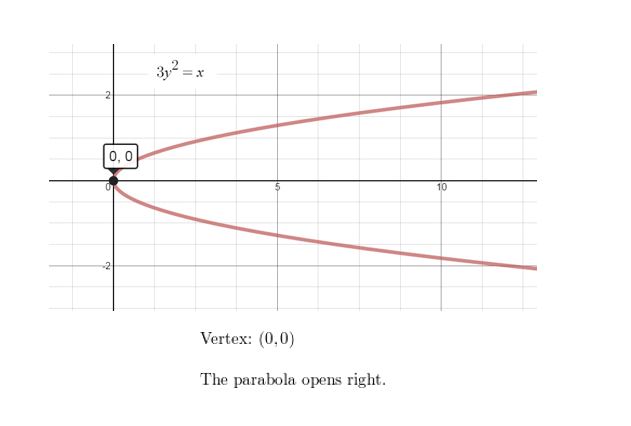
Question 53.
−8y2 + 2 = x
Answer:
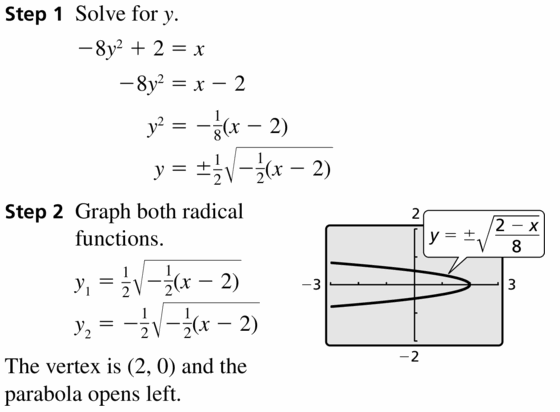
Question 54.
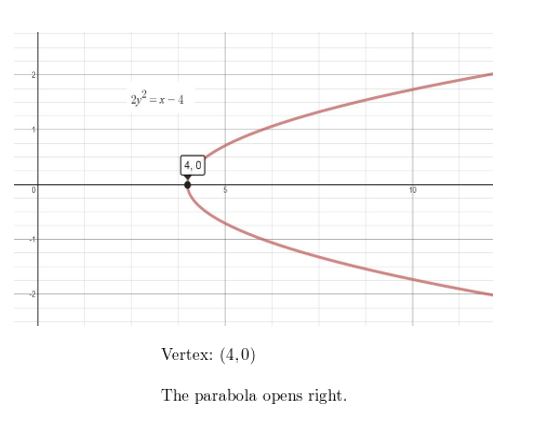
2y2 = x − 4
Answer:
Question 55.
x + 8 = \(\frac{1}{5}\)y2
Answer:

Question 56.
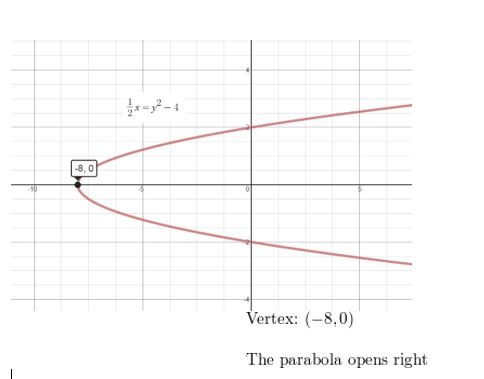
\(\frac{1}{2}\)x = y2 − 4
Answer:
In Exercises 57–62, use a graphing calculator to graph the equation of the circle. Identify the radius and the intercepts.
Question 57.
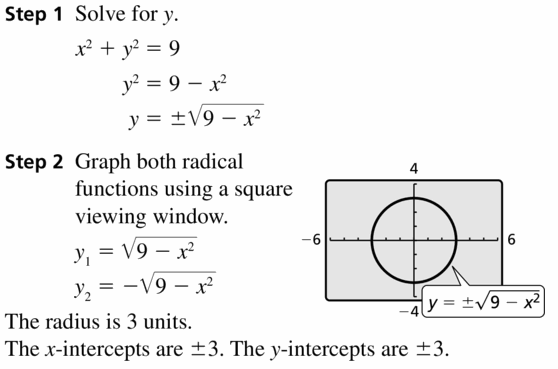
x2 + y2 = 9
Answer:
Question 58.
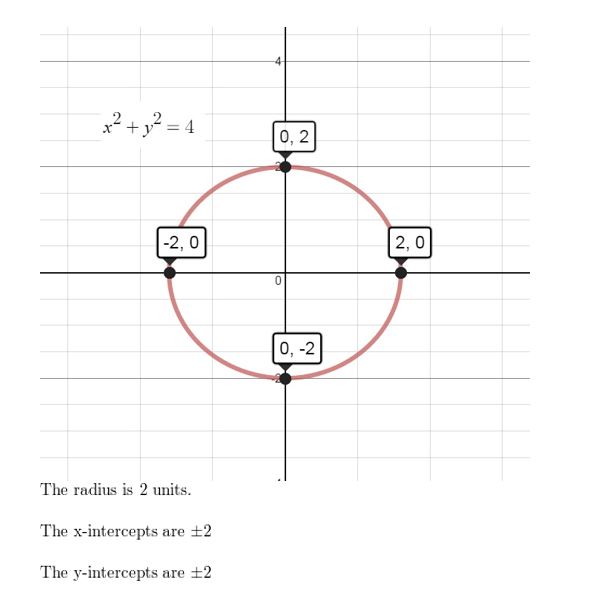
x2 + y2 = 4
Answer:
Question 59.
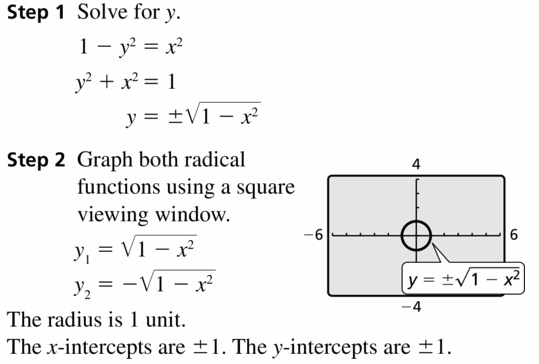
1 − y2 = x2
Answer:
Question 60.
64 − x2 = y2
Answer:
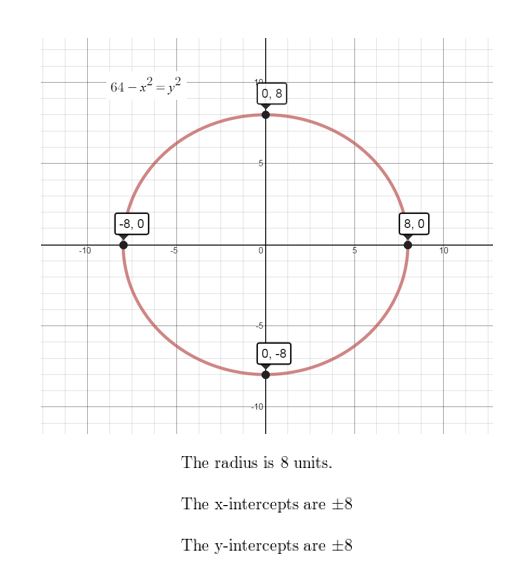
Question 61.
−y2 = x2 − 36
Answer:

Question 62.
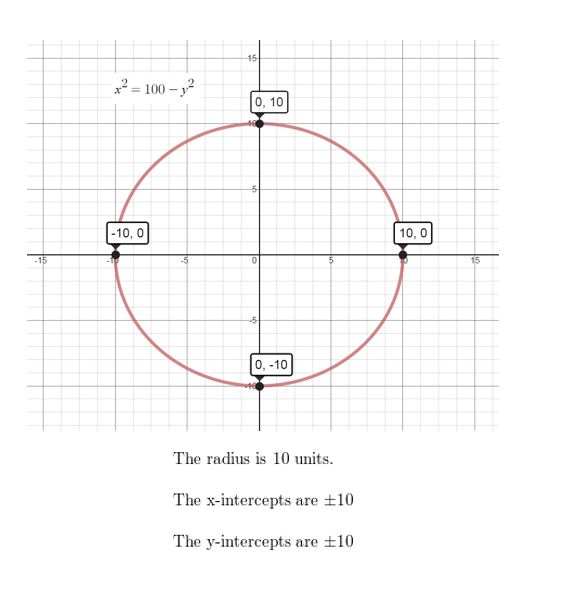
x2 = 100 − y2
Answer:
Question 63.
MODELING WITH MATHEMATICS The period of a pendulum is the time the pendulum takes to complete one back-and-forth swing. The period T (in seconds) can be modeled by the function T = 1.11\(\sqrt{\ell}\), where ℓ is the length (in feet) of the pendulum. Graph the function. Estimate the length of a pendulum with a period of 2 seconds. Explain your reasoning.

Answer:

Question 64.
HOW DO YOU SEE IT? Does the graph represent a square root function or a cube root function? Explain. What are the domain and range of the function?
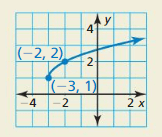
Answer:

Question 65.
PROBLEM SOLVING For a drag race car with a total weight of 3500 pounds, the speed s(in miles per hour) at the end of a race can be modeled by s = 14.8\(\sqrt[3]{p}\), where p is the power (in horsepower). Graph the function.
a. Determine the power of a 3500-pound car that reaches a speed of 200 miles per hour.
b. What is the average rate of change in speed as the power changes from 1000 horsepower to 1500 horsepower?
Answer:
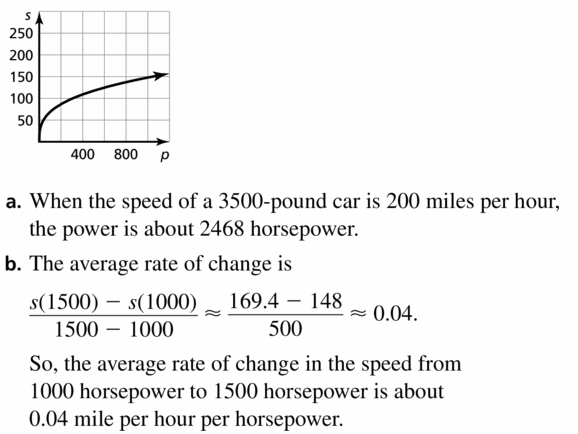
Question 66.
THOUGHT PROVOKING The graph of a radical function f passes through the points (3, 1) and (4, 0). Write two different functions that could represent f(x + 2) + 1. Explain.
Answer:
Question 67.
MULTIPLE REPRESENTATIONS The terminal velocity vt(in feet per second) of a skydiver who weighs 140 pounds is given by vt = 33.7\(\sqrt{\frac{140}{\Lambda}}\)
where A is the cross-sectional surface area (in square feet) of the skydiver. The table shows the terminal velocities (in feet per second) for various surface areas (in square feet) of a skydiver who weighs 165 pounds.
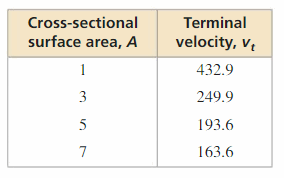
a. Which skydiver has a greater terminal velocity for each value of A given in the table?
b. Describe how the different values of A given in the table relate to the possible positions of the falling skydiver.
Answer:

Question 68.
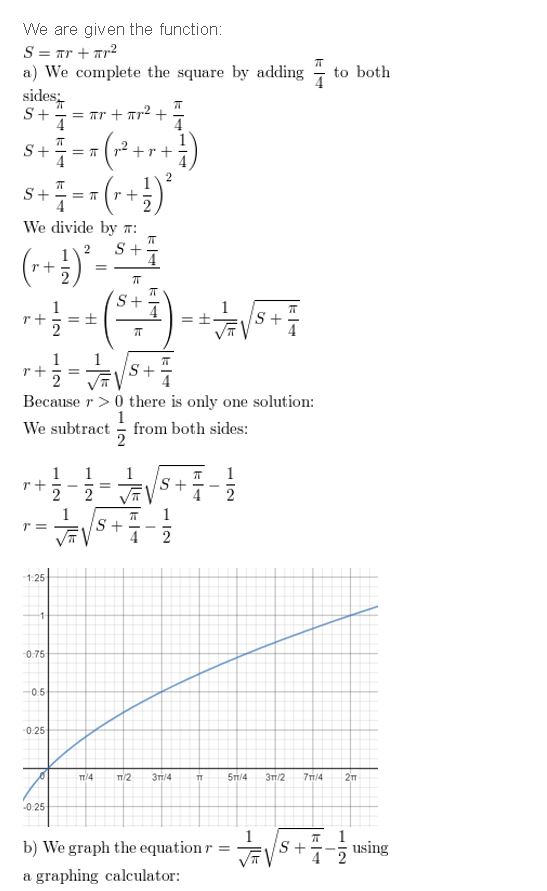
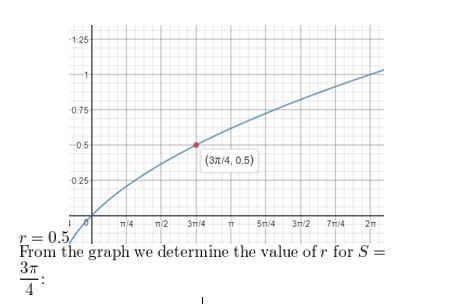
MATHEMATICAL CONNECTIONS The surface area S of a right circular cone with a slant height of 1 unit is given by S = πr + πr2, where r is the radius of the cone.
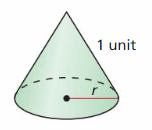
a. Use completing the square to show that r = \(\frac{1}{\sqrt{\pi}} \sqrt{S+\frac{\pi}{4}}-\frac{1}{2}\).
b. Graph the equation in part (a) using a graphing calculator. Then find the radius of a right circular cone with a slant height of 1 unit and a surface area of \(\frac{3 \pi}{4}\) square units.
Answer:
Maintaining Mathematical Proficiency
Solve the equation. Check your solutions. (Skills Review Handbook)
Question 69.
| 3x + 2 | = 5
Answer:
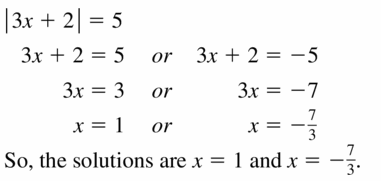
Question 70.
∣4x + 9 ∣ = −7
Answer:
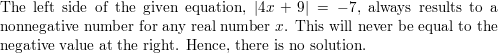
Question 71.
| 2x − 6 ∣ = ∣ x ∣
Answer:
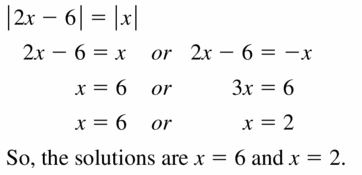
Question 72.
| x + 8 | = | 2x + 2 |
Answer:
Given,
| x + 8 | = | 2x + 2 |
x + 8 = 2x + 2
x – 2x = 2 – 8
-x = -6
x = 6
x + 8 = -2x – 2
x + 2x = -2 – 8
3x = -10
x = -10/3
Solve the inequality. (Section 3.6)
Question 73.
x2 + 7x + 12 < 0
Answer:

Question 74.
x2 − 10x + 25 ≥ 4
Answer:
Question 75.
2x2 + 6 > 13x
Answer:

Question 76.
\(\frac{1}{8}\)x2 + x ≤ −2
Answer:
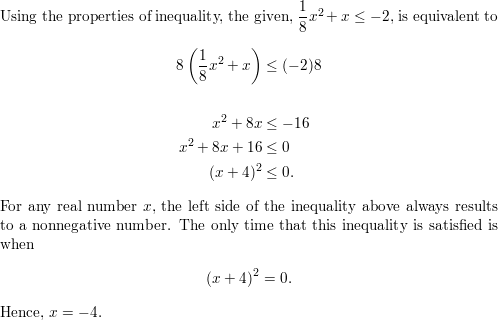
Rational Exponents and Radical Functions Study Skills : Analyzing Your Errors
5.1–5.3 What Did You Learn?
Core Vocabulary

Core Concepts
Section 5.1
Real nth Roots of a, p. 238
Rational Exponents, p. 239
Section 5.2
Properties of Rational Exponents, p. 244
Properties of Radicals, p. 245
Section 5.3
Parent Functions for Square Root and Cube Root Functions, p. 252
Transformations of Radical Functions, p. 253
Mathematical Practices
Question 1.
How can you use definitions to explain your reasoning in Exercises 21–24 on page 241?
Question 2.
How did you use structure to solve Exercise 76 on page 250?
Question 3.
How can you check that your answer is reasonable in Exercise 39 on page 257?
Question 4.
How can you make sense of the terms of the surface area formula given in Exercise 68 on page 258?
Study Skills
Analyzing Your Errors
Application Errors
What Happens: You can do numerical problems, but you struggle with problems that have context.

How to Avoid This Error: Do not just mimic the steps of solving an application problem. Explain out loud what the question is asking and why you are doing each step. After solving the problem, ask yourself, “Does my solution make sense?”
Rational Exponents and Radical Functions 5.1 – 5.3 Quiz
5.1–5.3 Quiz
Find the indicated real nth root(s) of a. (Section 5.1)
Question 1.
n = 4, a = 81
Answer: 3 and -3
Explanation:
Given,
\(\sqrt[n]{a}\)
where, n = 4, a = 81
\(\sqrt[4]{81}\)
The nth root is even so its root will be negative or positive.
The root of this is a number when multiplied by itself 4 times will give 81.
81 is odd and is a multiple of 3 and 9 so it is likely 3.
3 × 3 × 3 × 3 = 81
-3 × -3 × -3 × -3 = 81
The real nth root are 3 and -3
Question 2.
n = 5, a = −1024
Answer: -5
Explanation:
Given,
\(\sqrt[5]{-1024}\)
The nth root when n is, even so, the root will be negative or positive.
The root of this is a number when multiplied by itself 5 times will give 1024.
1024 is even and is multiple.
-5 × -5 × -5 × -5 × -5 = -1024
The real nth root of a is -5.
Question 3.
Evaluate (a) 163/4 and (b) 1252/3 without using a calculator. Explain your reasoning. (Section 5.1)
Answer:
(a) 163/4
\(\sqrt[4]{16^3}\)
= \(\sqrt[4]{4096}\)
= 8
(b) 1252/3
\(\sqrt[3]{125^2}\)
\(\sqrt[3]{15625}\)
= 25
Find the real solution(s) of the equation. Round your answer to two decimal places.(Section 5.1)
Question 4.
2x6 = 1458
Answer: x = 3
Explanation:
Given,
2x6 = 1458
x6 = 1458/2
x6 = 729
x6 = 36
x = 3
The real solution of the equation is x = 3.
Question 5.
(x + 6)3 = 28
Answer: x(x² + 18x + 108) = -188
Explanation:
Given,
(x + 6)3 = 28
This is in the form of (a + b)³ = a³ + b³ + 3a²b + 3ab²
(x)³ + (6)³ + 3(x)²(6) + 3(x)(6)² = 28
x³ + 216 + 18x² + 108x = 28
x³ + 18x² + 108x = 28 – 216
x³ + 18x² + 108x = – 188
x(x² + 18x + 108) = -188
So, the equation is x(x² + 18x + 108) = -188
Simplify the expression.(Section 5.2)
Question 6.
\(\left(\frac{48^{1 / 4}}{6^{1 / 4}}\right)^{6}\)
Question 7.
\(\sqrt[4]{3}\) • \(\sqrt[4]{432}\)
Question 8.
\(\frac{1}{3+\sqrt{2}}\)
Question 9.
\(\sqrt[3]{16}\) – \(5 \sqrt[3]{2}\)
Question 10.
Simplify \(\sqrt[8]{x^{9} y^{8} z^{16}}\). (Section 5.2)
Write the expression in simplest form. Assume all variables are positive.(Section 5.2)
Question 11.
\(\sqrt[3]{216 p^{9}}\)
Question 12.
\(\frac{\sqrt[5]{32}}{\sqrt[5]{m^{3}}}\)
Question 13.
\(\sqrt[4]{n^{4} q}\) + \(7 n \sqrt[4]{q}\)
Question 14.
Graph f(x) = 2\(2 \sqrt[3]{x}\) + 1. Identify the domain and range of the function. (Section 5.3)
Describe the transformation of the parent function represented by the graph of g. Then write a rule for g.(Section 5.3)
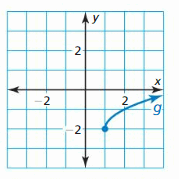
Question 15.
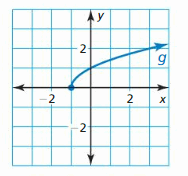
Question 16.
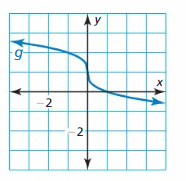
Question 17.
Question 18.
Use a graphing calculator to graph x = 3y2 − 6. Identify the vertex and direction the parabola opens. (Section 5.3)
Question 19.
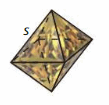
A jeweler is setting a stone cut in the shape of a regular octahedron. A regular octahedron is a solid with eight equilateral triangles as faces, as shown. The formula for the volume of the stone is V= 0.47s3, where s is the side length (in millimeters) of an edge of the stone. The volume of the stone is 161 cubic millimeters. Find the length of an edge of the stone. (Section 5.1)
Question 20.
An investigator can determine how fast a car was traveling just prior to an accident using the model s = 4\(\sqrt{d}\), where s is the speed (in miles per hour) of the car and d is the length (in feet) of the skid marks. Graph the model. The length of the skid marks of a car is 90 feet. Was the car traveling at the posted speed limit prior to the accident? Explain your reasoning. (Section 5.3)

Lesson 5.4 Solving Radical Equations and Inequalities
Essential Question
How can you solve a radical equation?
EXPLORATION 1
Solving Radical Equations
Work with a partner. Match each radical equation with the graph of its related radical function. Explain your reasoning. Then use the graph to solve the equation, if possible. Check your solutions.
a. \(\sqrt{x-1}\) – 1 = 0
b. \(\sqrt{2 x+2}\) – \(\sqrt{x+4}\) = 0
c. \(\sqrt{9-x^{2}}\) = 0
d. \(\sqrt{x+2}\) – x = 0
e. \(\sqrt{-x+2}\) – x = 0
f. \(\sqrt{3 x^{2}+1}\) = 0
EXPLORATION 2
Solving Radical Equations
Work with a partner. Look back at the radical equations in Exploration 1. Suppose that you did not know how to solve the equations using a graphical approach.
a. Show how you could use a numerical approach to solve one of the equations. For instance, you might use a spreadsheet to create a table of values.

b. Show how you could use an analytical approach to solve one of the equations. For instance, look at the similarities between the equations in Exploration 1. What first step may be necessary so you could square each side to eliminate the radical(s)? How would you proceed to find the solution?
Communicate Your Answer
Question 3.
How can you solve a radical equation?
Question 4.
Would you prefer to use a graphical, numerical, or analytical approach to solve the given equation? Explain your reasoning. Then solve the equation.
\(\sqrt{x+3}\) – \(\sqrt{x-2}\) = 1
Monitoring Progress
Solve the equation. Check your solution.
Question 1.
\(\sqrt[3]{x}\) – 9 = -6
Answer:
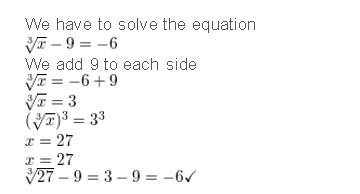
Question 2.
\(\sqrt{x+25}\) = 2
Answer:
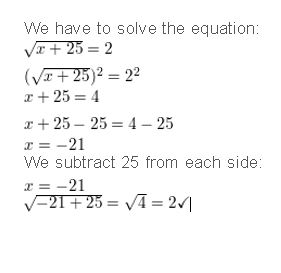
Question 3.
2\(\sqrt[3]{x-3}\) = 4
Answer:
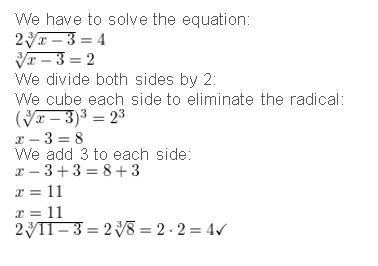
Question 4.
WHAT IF? Estimate the air pressure at the center of the hurricane when the mean sustained wind velocity is 48.3 meters per second.
Answer:

Solve the equation. Check your solution(s).
Question 5.
\(\sqrt{10 x+9}\) = x + 3
Answer:
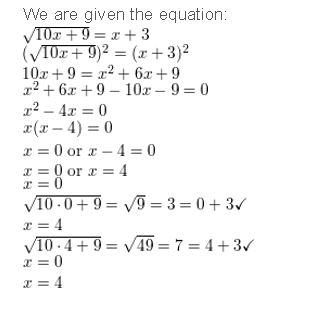
Question 6.
\(\sqrt{2 x+5}\) = \(\sqrt{x+7}\)
Answer:
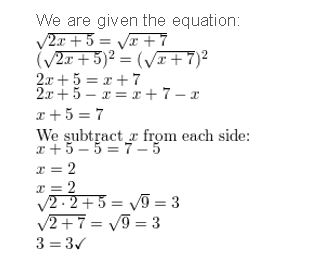
Question 7.
\(\sqrt{x+6}\) – 2 = \(\sqrt{x-2}\)
Answer:
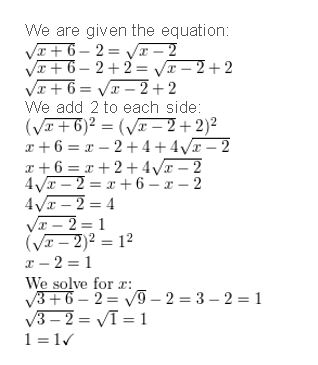
Solve the equation. Check your solution(s).
Question 8.
(3x)1/3 = −3
Answer:
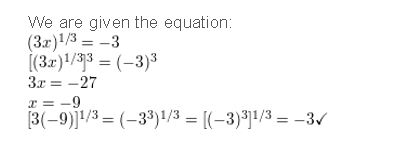
Question 9.
(x + 6)1/2 = x
Answer:
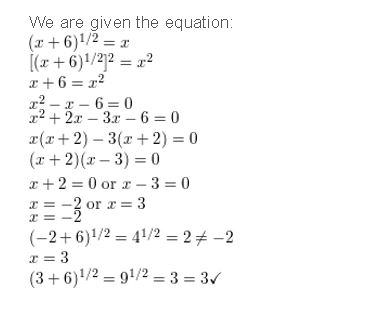
Question 10.
(x + 2)3/4 = 8
Answer:
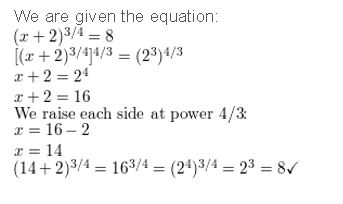
Question 11.
Solve
(a) 2\(\sqrt{x}\) − 3 ≥ 3 and
(b) 4\(\sqrt[3]{x+1}\) < 8
Answer:

Solving Radical Equations and Inequalities 5.4 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY Is the equation 3x − \(\sqrt{2}\) = \(\sqrt{6}\) a radical equation? Explain your reasoning.
Answer:
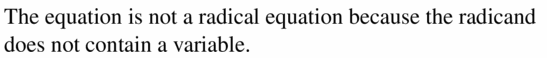
Question 2.
WRITING Explain the steps you should use to solve \(\sqrt{x}\) + 10 < 15
Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 3–12, solve the equation. Check your solution.
Question 3.
\(\sqrt{5 x+1}\) = 6
Answer:

Question 4.
\(\sqrt{3 x+10}\) = 8
Answer:
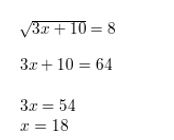
Question 5.
\(\sqrt[3]{x-16}\) = 2
Answer:

Question 6.
\(\sqrt[3]{x}\) − 10 = −7
Answer:
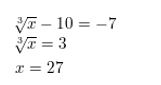
Question 7.
−2\(\sqrt{24 x}\) + 13 = −1
Answer:

Question 8.
8\(\sqrt[3]{10 x}\) − 15 = 17
Answer:
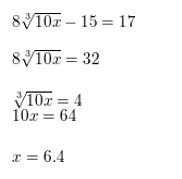
Question 9.
\(\frac{1}{5} \sqrt[3]{3 x}\) = 8
Answer:

Question 10.
\(\sqrt{2 x}-\frac{2}{3}\) = 0
Answer:
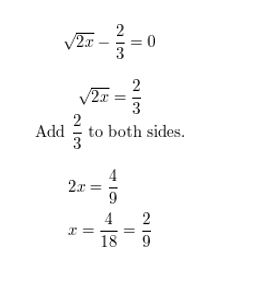
Question 11.
\(2 \sqrt[5]{x}\) + 7 = 15
Answer:

Question 12.
\(\sqrt[4]{4 x}\) − 13 = −15
Answer:
Question 13.
MODELING WITH MATHEMATICS Biologists have discovered that the shoulder height h (in centimeters) of a male Asian elephant can be modeled by h = 62.5\(\sqrt[3]{t}\) + 75.8, where t is the age (in years) of the elephant. Determine the age of an elephant with a shoulder height of 250 centimeters.

Answer:

Question 14.
MODELING WITH MATHEMATICS In an amusement park ride, a rider suspended by cables swings back and forth from a tower. The maximum speed v (in meters per second) of the rider can be approximated by v = \(\sqrt{2 g h}\), where h is the height (in meters) at the top of each swing and g is the acceleration due to gravity (g ≈ 9.8 m/sec2). Determine the height at the top of the swing of a rider whose maximum speed is 15 meters per second.
Answer:

In Exercises 15–26, solve the equation. Check your solution(s).
Question 15.
x− 6 = \(\sqrt{3 x}\)
Answer:

Question 16.
x − 10 = \(\sqrt{9 x}\)
Answer:
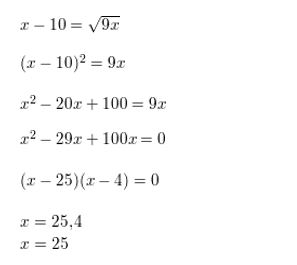
Question 17.
\(\sqrt{44-2 x}\) = x − 10
Answer:

Question 18.
\(\sqrt{2 x+30}\) = x + 3
Answer:
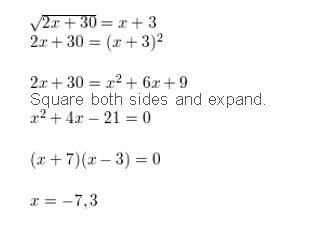
Question 19.
\(\sqrt[3]{8 x^{3}-1}\) = 2x − 1
Answer:
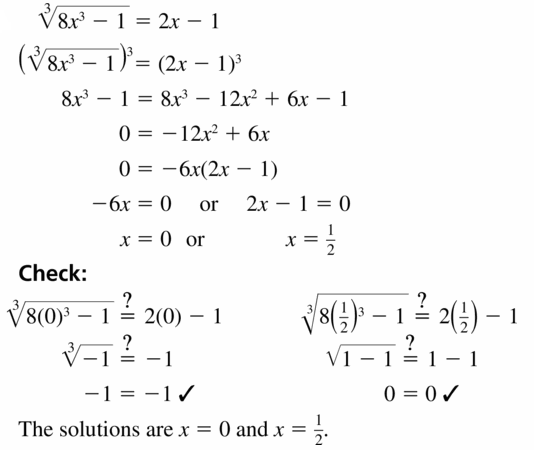
Question 20.
\(\sqrt[4]{3-8 x^{2}}\) = 2x
Answer:

Question 21.
\(\sqrt{4 x+1}\) = \(\sqrt{x+10}\)
Answer:

Question 22.
\(\sqrt{3 x-3}\) – \(\sqrt{x+12}\) = 0
Answer:

Question 23.
\(\sqrt[3]{2 x-5}\) – \(\sqrt[3]{8 x+1}\) = 0
Answer:
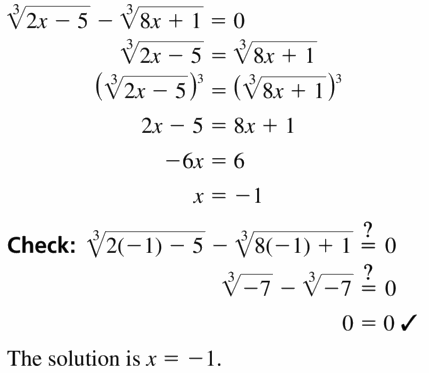
Question 24.
\(\sqrt[3]{x+5}\) = 2\(\sqrt[3]{2 x+6}\)
Answer:

Question 25.
\(\sqrt{3 x-8}\) + 1 = \(\sqrt{x+5}\)
Answer:
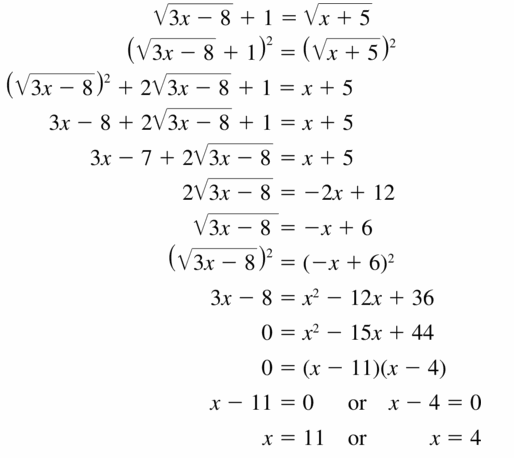

Question 26.
\(\sqrt{x+2}\) = 2 – \(\sqrt{x}\)
Answer:

In Exercises 27–34, solve the equation. Check your solution(s).
Question 27.
2x2/3 = 8
Answer:

Question 28.
4x3/2 = 32
Answer:
Given,
4x3/2 = 32
x = 32/4
x3/2 = 8
\(\sqrt{x³}\) = 8
Squaring on both sides
x³ = 64
x³ = 4³
x = 4
Question 29.
x1/4 + 3 = 0
Answer:

Question 30.
2x3/4 − 14 = 40
Answer:
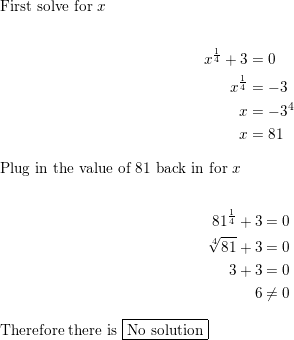
Question 31.
(x + 6)1/2 = x
Answer:
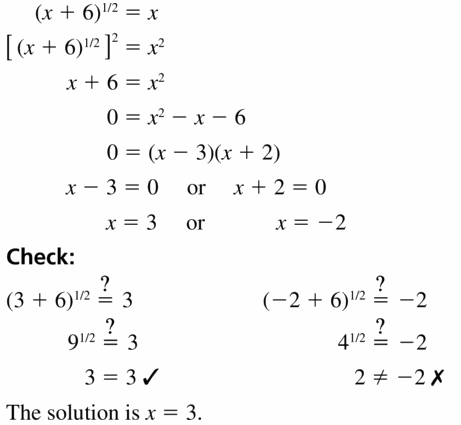
Question 32.
(5 − x)1/2 − 2x = 0
Answer:
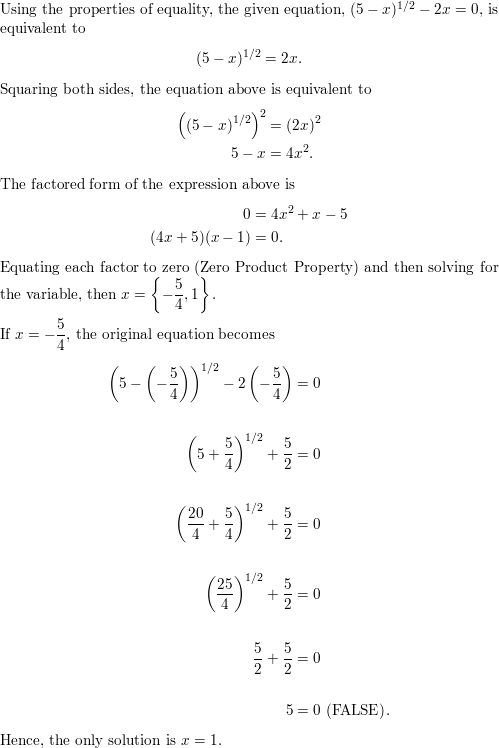
Question 33.
2(x + 11)1/2 = x + 3
Answer:
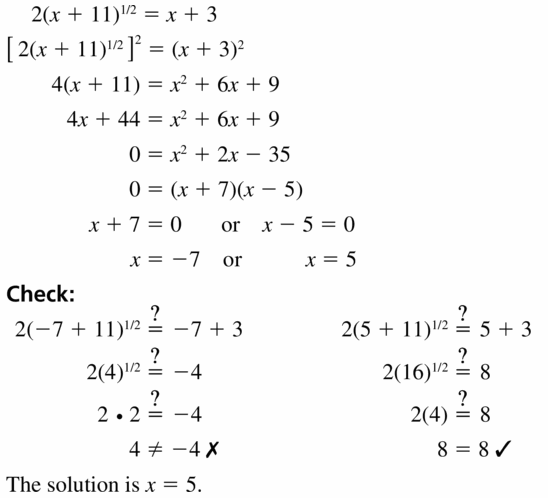
Question 34.
(5x2 − 4)1/4 = x
Answer:
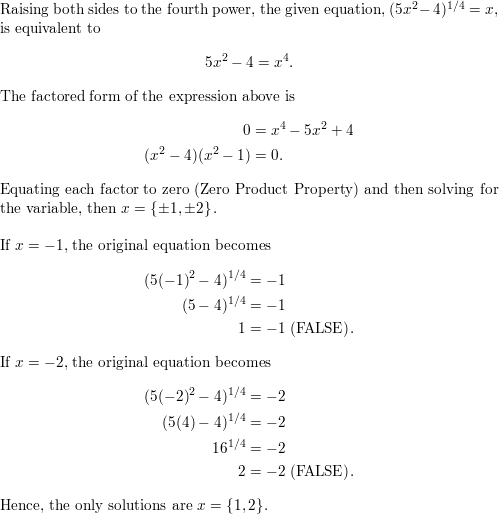
ERROR ANALYSIS In Exercises 35 and 36, describe and correct the error in solving the equation.
Question 35.
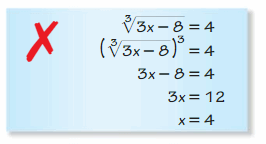
Answer:

Question 36.
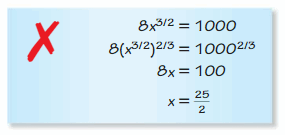
Answer:
In Exercises 37–44, solve the inequality.
Question 37.
\(2 \sqrt[3]{x}\) − 5 ≥ 3
Answer:
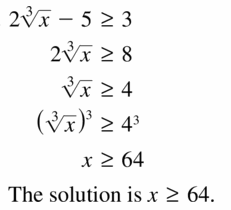
Question 38.
\(\sqrt[3]{x-4}\) ≤ 5
Answer:
Given,
\(\sqrt[3]{x-4}\) ≤ 5
Apply Cubing on both sides
(x – 4) ≤ 5³
x-4 ≤ 125
x ≤ 125 + 4
x ≤ 129
Question 39.
\(4 \sqrt{x-2}\) > 20
Answer:
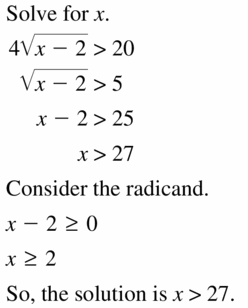
Question 40.
7\(\sqrt{x}\) + 1 < 9
Answer:

Question 41.
2\(\sqrt{x}\) + 3 ≤ 8
Answer:
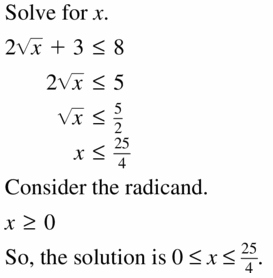
Question 42.
\(\sqrt[3]{x+7}\) ≥ 3
Answer:
Question 43.
\(-2 \sqrt[3]{x+4}\) < 12
Answer:
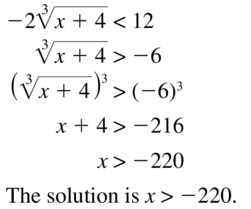
Question 44.
−0.25\(\sqrt{x}\) − 6 ≤ −3
Answer:
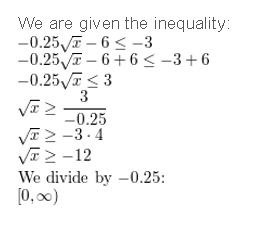
Question 45.
MODELING WITH MATHEMATICS The length ℓ (in inches) of a standard nail can be modeled by ℓ = 54d3/2, where d is the diameter (in inches) of the nail. What is the diameter of a standard nail that is 3 inches long?
Answer:

Question 46.
DRAWING CONCLUSIONS “Hang time” is the time you are suspended in the air during a jump. Your hang time t (in seconds) is given by the function t = 0.5\(\sqrt{h}\), where h is the height (in feet) of the jump. Suppose a kangaroo and a snowboarder jump with the hang times shown.

a. Find the heights that the snowboarder and the kangaroo jump.
b. Double the hang times of the snowboarder and the kangaroo and calculate the corresponding heights of each jump.
c. When the hang time doubles, does the height of the jump double? Explain.
Answer:

USING TOOLS In Exercises 47–52, solve the nonlinear system. Justify your answer with a graph.
Question 47.
y2 = x − 3
y = x − 3
Answer:

Question 48.
y2 = 4x + 17
y = x + 5
Answer:
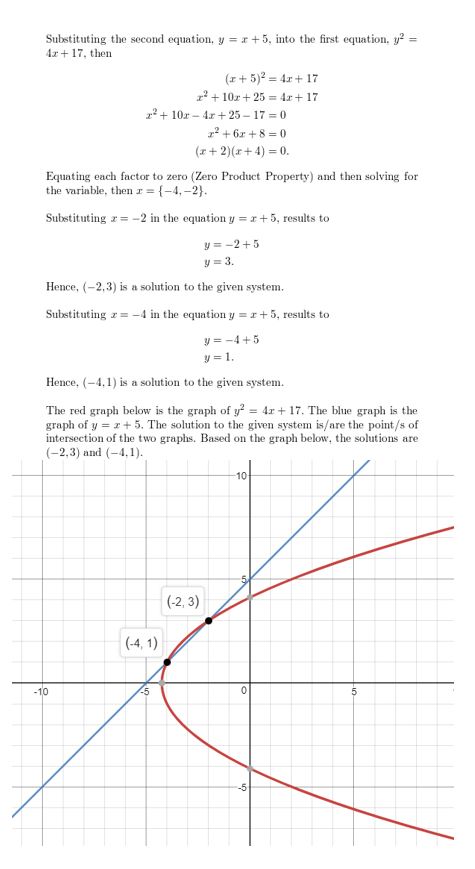
Question 49.
x2 + y2 = 4
y = x – 2
Answer:
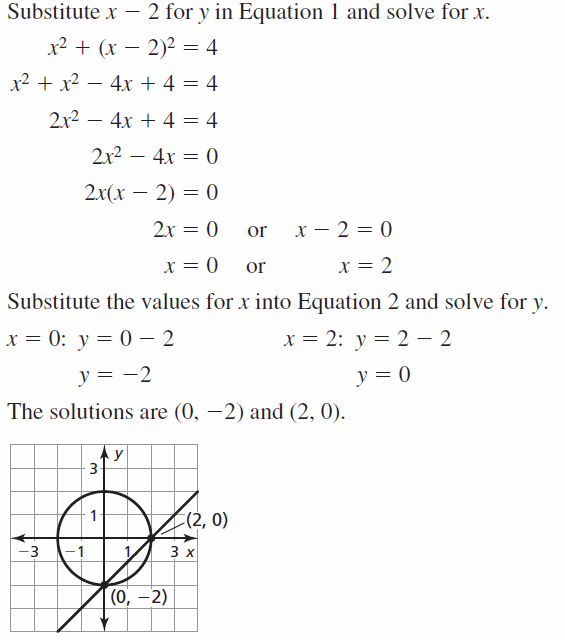
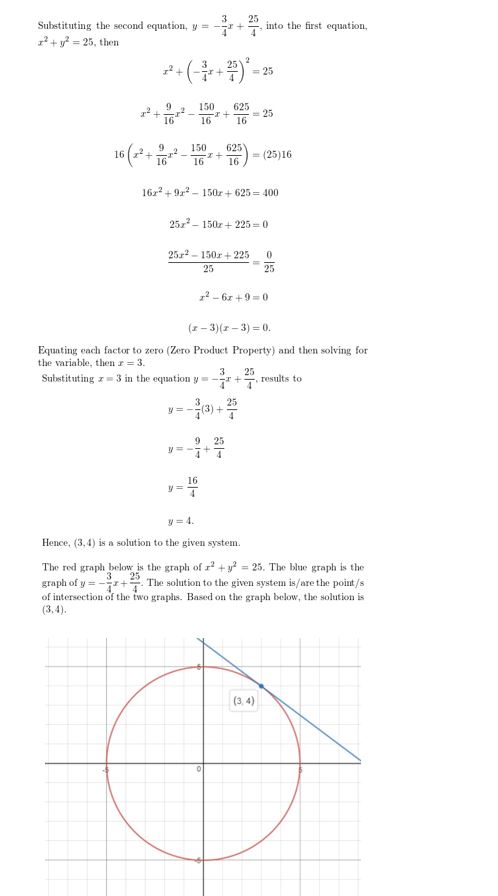
Question 50.
x2 + y2 = 25
y = \(-\frac{3}{4}\)x + \(\frac{25}{4}\)
Answer:
Question 51.
x2 + y2 = 1
y = \(\frac{1}{2}\)x2 – 1
Answer:

Question 52.
x2 + y2 = 4
y2 = x + 2
Answer:
Question 53.
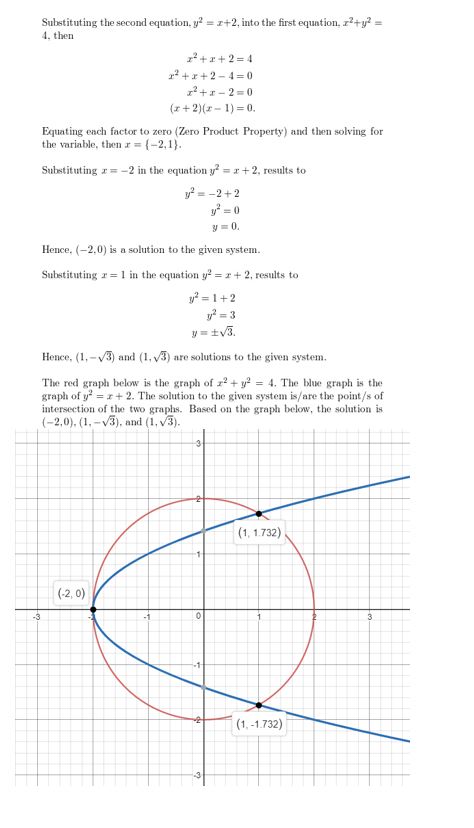
PROBLEM SOLVING The speed s (in miles per hour) of a car can be given by s = \(\sqrt{30 f d}\), where f is the coefficient of friction and d is the stopping distance (in feet). The table shows the coefficient of friction for different surfaces.
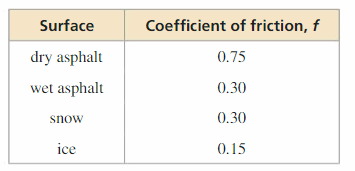
a. Compare the stopping distances of a car traveling 45 miles per hour on the surfaces given in the table.
b. You are driving 35 miles per hour on an icy road when a deer jumps in front of your car. How far away must you begin to brake to avoid hitting the deer? Justify your answer.
Answer:


Question 54.
MODELING WITH MATHEMATICS The Beaufort wind scale was devised to measure wind speed. The Beaufort numbers B, which range from 0 to 12, can be modeled by B = 1.69\(\sqrt{s+4.25}\) − 3.55, where s is the wind speed (in miles per hour).
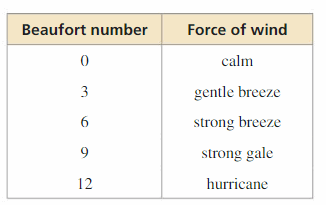
a. What is the wind speed for B = 0? B = 3?
b. Write an i
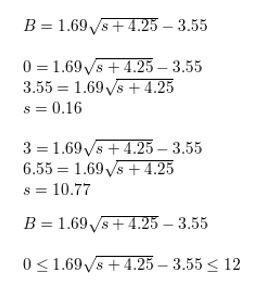
Question 55.
USING TOOLS Solve the equation x − 4 = \(\sqrt{2 x}\). Then solve the equation x − 4 = − \(\sqrt{2 x}\).
a. How does changing \(\sqrt{2 x}\) to −\(\sqrt{2 x}\) change the solution(s) of the equation?
b. Justify your answer in part (a) using graphs.
Answer:


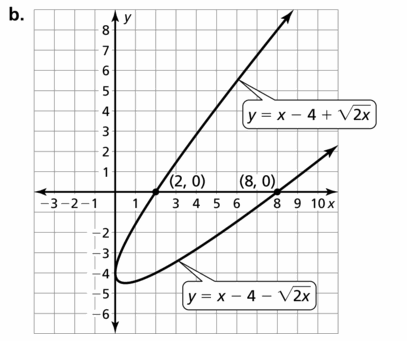
Question 56.
MAKING AN ARGUMENT Your friend says it is impossible for a radical equation to have two extraneous solutions. Is your friend correct? Explain your reasoning.
Answer:
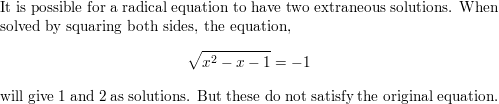
Question 57.
USING STRUCTURE Explain how you know the radical equation \(\sqrt{x+4}\) = −5 has no real solution without solving it.
Answer:

Question 58.
HOW DO YOU SEE IT? Use the graph to find the solution of the equation 2\(\sqrt{x-4}\) = −\(\sqrt{x-1}\) + 4. Explain your reasoning.
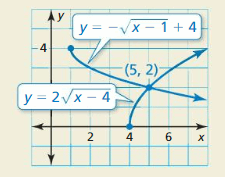
Answer:
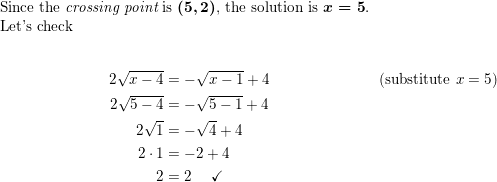
Question 59.
WRITING A company determines that the price p of a product can be modeled by p = 70 − \(\sqrt{0.02 x+1}\), where x is the number of units of the product demanded per day. Describe the effect that raising the price has on the number of units demanded.
Answer:
Question 60.
THOUGHT PROVOKING City officials rope off a circular area to prepare for a concert in the park. They estimate that each person occupies 6 square feet. Describe how you can use a radical inequality to determine the possible radius of the region when P people are expected to attend the concert.

Answer:
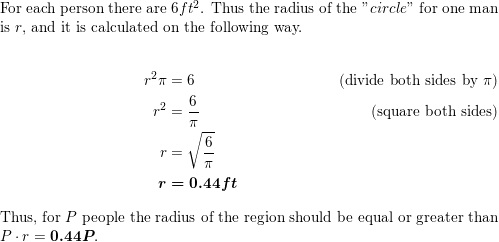
Question 61.
MATHEMATICAL CONNECTIONS The Moeraki Boulders along the coast of New Zealand are stone spheres with radii of approximately 3 feet. A formula for the radius of a sphere is
r = \(\frac{1}{2} \sqrt{\frac{S}{\pi}}\)
where S is the surface area of the sphere. Find the surface area of a Moeraki Boulder.
Answer:

Question 62.
PROBLEM SOLVING You are trying to determine the height of a truncated pyramid, which cannot be measured directly. The height h and slant heightℓof the truncated pyramid are related by the formula below.
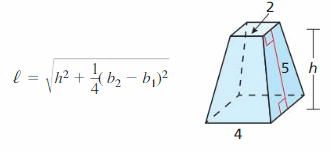
In the given formula, b1 and b2 are the side lengths of the upper and lower bases of the pyramid, respectively. When ℓ = 5, b1 = 2, and b2 = 4, what is the height of the pyramid?
Answer:
Question 63.
REWRITING A FORMULA A burning candle has a radius of r inches and was initially h0inches tall. After t minutes, the height of the candle has been reduced to h inches. These quantities are related by the formula
r = \(\sqrt{\frac{k t}{\pi\left(h_{0}-h\right)}}\)
where k is a constant. Suppose the radius of a candle is 0.875 inch, its initial height is 6.5 inches, and k = 0.04.
a. Rewrite the formula, solving for h in terms of t.
b. Use your formula in part (a) to determine the height of the candle after burning 45 minutes.
Answer:
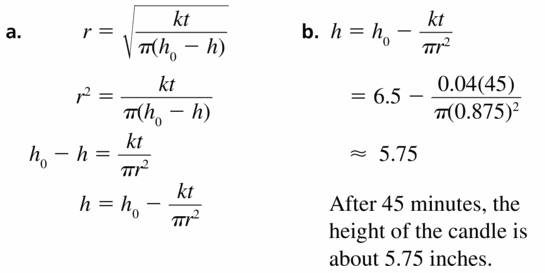
Maintaining Mathematical Proficiency
Perform the indicated operation. (Section 4.2 and Section 4.3)
Question 64.
(x3 − 2x2 + 3x + 1) + (x4 − 7x)
Answer:
x4 − 7x + x3 − 2x2 + 3x + 1
= x4 + x3 − 2x2 − 7x + 3x + 1
= x4 + x3 − 2x2 − 4x + 1
So, (x3 − 2x2 + 3x + 1) + (x4 − 7x) = x4 + x3 − 2x2 − 4x + 1
Question 65.
(2x5 + x4 − 4x2) − (x5 − 3)
Answer:
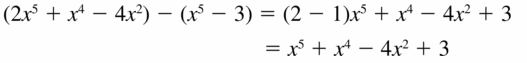
Question 66.
(x3 + 2x2 + 1)(x2 + 5)
Answer:
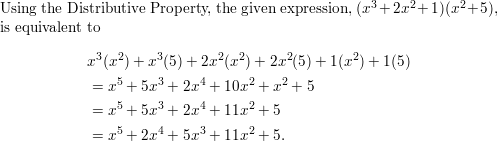
Question 67.
(x4 + 2x3 + 11x2 + 14x − 16) ÷ (x + 2)
Answer:
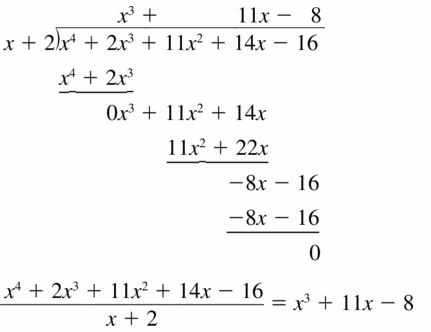
Let f(x) = x3 – 4x2 + 6. Write a rule for g. Describe the graph of g as a transformation of the graph of f.(Section 4.7)
Question 68.
g(x) = f(−x) + 4
Answer:
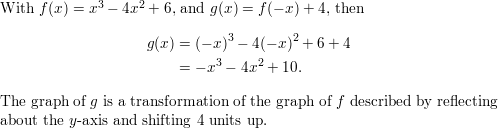
Question 69.
g(x) = \(\frac{1}{2}\)f(x) − 3
Answer:

Question 70.
g(x) = −f(x − 1) + 6
Answer:

Lesson 5.5 Performing Function Operations
Essential Question
How can you use the graphs of two functions to sketch the graph of an arithmetic combination of the two functions?
Just as two real numbers can be combined by the operations of addition, subtraction, multiplication, and division to form other real numbers, two functions can be combined to form other functions. For example, the functions f(x) = 2x − 3 and g(x) = x2 − 1 can be combined to form the sum, difference, product, or quotient of f and g.
f(x) + g(x) = (2x − 3) + (x2 − 1) = x2 + 2x − 4 sum
f(x) − g(x) = (2x − 3) − (x2 − 1) = −x2 + 2x − 2 difference
f(x) • g(x) = (2x − 3)(x2 − 1) = 2x3 − 3x2 − 2x + 3 product

EXPLORATION 1
Graphing the Sum of Two Functions
Work with a partner. Use the graphs of f and g to sketch the graph of f + g. Explain your steps.
Sample Choose a point on the graph of g. Use a compass or a ruler to measure its distance above or below the x-axis. If above, add the distance to the y-coordinate of the point with the same x-coordinate on the graph of f. If below, subtract the distance. Plot the new point. Repeat this process for several points. Finally, draw a smooth curve through the new points to obtain the graph of f + g.
Communicate Your Answer
Question 2.
How can you use the graphs of two functions to sketch the graph of an arithmetic combination of the two functions?

Question 3.
Check your answers in Exploration 1 by writing equations for f and g, adding the functions, and graphing the sum.
5.5 Lesson
Monitoring Progress
Question 1.
Let f(x) = −2x2/3 and g(x) = 7x2/3. Find (f + g)(x) and (f − g)(x) and state the domain of each. Then evaluate (f + g)(8) and (f − g)(8).
Answer:

Question 2.
Let f(x) = 3x and g(x) = x1/5. Find (fg)(x) and (\(\frac{f}{g}\))(x) and state the domain of each. Then evaluate (fg)(32) and (\(\frac{f}{g}\))(32).
Answer:

Question 3.
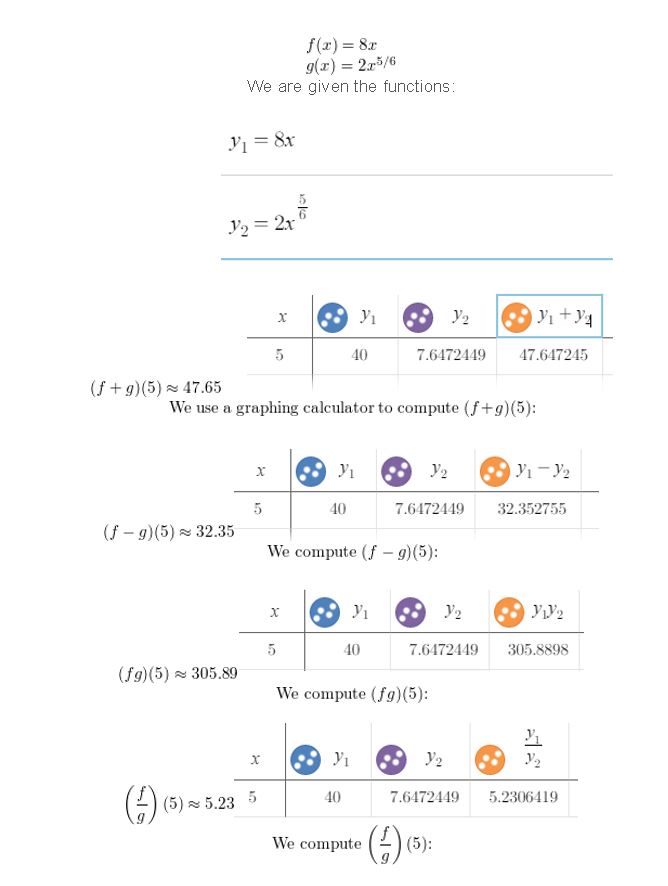
Let f(x) = 8x and g(x) = 2x5/6. Use a graphing calculator to evaluate (f + g)(x), (f − g)(x), (fg)(x), and (\(\frac{f}{g}\)) (x) when x = 5. Round your answers to two decimal places.
Answer:
Question 4.
In Example 5, explain why you can evaluate (f + g)(3), (f − g)(3), and (fg)(3) but not (\(\frac{f}{g}\))(3).
Answer:

Question 5.
Use the answer in Example 6(a) to find the total number of heartbeats over the lifetime of a white rhino when its body mass is 1.7 × 105 kilograms.
Answer:

Performing Function Operations 5.5 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING Let f and g be any two functions. Describe how you can use f, g, and the four basic operations to create new functions.
Answer:
![]()
Question 2.
WRITING What x-values are not included in the domain of the quotient of two functions?
Answer:
Monitoring Progress and Modeling with Mathematics
In Exercises 3–6, find (f + g)(x) and (f – g)(x) and state the domain of each. Then evaluate f + g and f – g for the given value of x.
Question 3.
f(x) = \(-5 \sqrt[4]{x}\), g(x) = 19\(\sqrt[4]{x}\); x = 16
Answer:
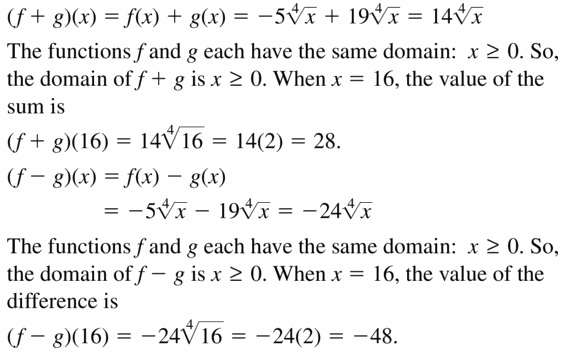
Question 4.
f(x) = \(\sqrt[3]{2 x}\), g(x) = −11\(\sqrt[3]{2 x}\) ; x = −4
Answer:
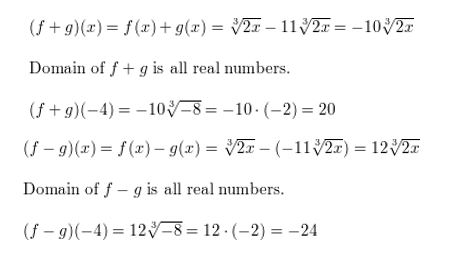
Question 5.
f(x) = 6x − 4x2− 7x3, g(x) = 9x2− 5x; x = −1
Answer:

Question 6.
f(x) = 11x + 2x2, g(x) = −7x − 3x2 + 4; x = 2
Answer:
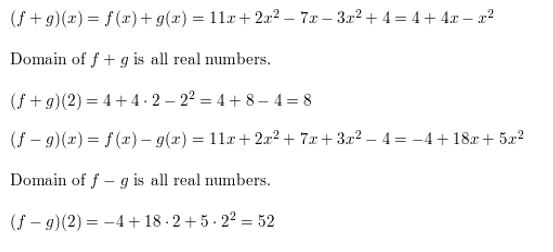
In Exercises 7–12, find (fg)(x) and (\(\frac{f}{g}\))(x) and state the domain of each. Then evaluate fg and \(\frac{f}{g}\) for the given value of x.
Question 7.
f(x) = 2x3, g(x) = \(\sqrt[3]{x}\) ; x = −27
Answer:

Question 8.
f(x) = x4, g(x) = \(3 \sqrt{x}\) ; x = 4
Answer:

Question 9.
f(x) = 4x, g(x) = 9x1/2; x = 9
Answer:
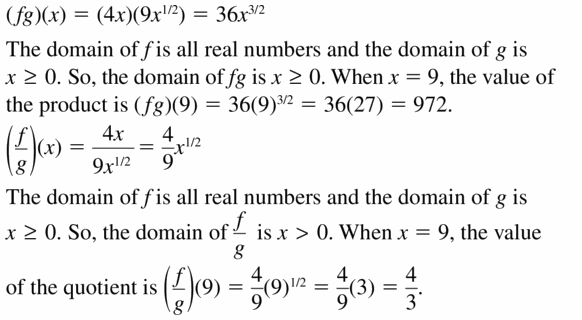
Question 10.
f(x) = 11x3, g(x) = 7x7/3; x = −8
Answer:

Question 11.
f(x) = 7x3/2, g(x) =−14x1/3; x = 64
Answer:

Question 12.
f(x) = 4x5/4, g(x) = 2x1/2; x = 16
Answer:

USING TOOLS In Exercises 13–16, use a graphing calculator to evaluate (f + g)(x), (f − g)(x), (fg)(x), and (\(\frac{f}{g}\))(x) when x = 5. Round your answers to two decimal places.
Question 13.
f(x) = 4x4; g(x) = 24x1/3
Answer:

Question 14.
f(x) = 7x5/3; g(x) = 49x2/3
Answer:
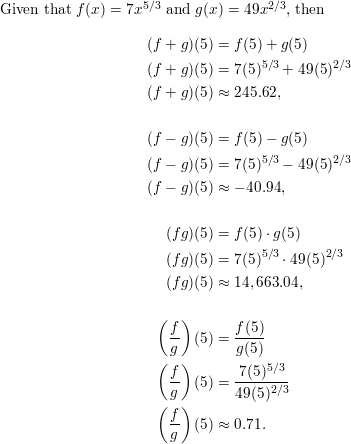
Question 15.
f(x) =−2x1/3; g(x) = 5x1/2
Answer:

Question 16.
f(x) = 4x1/2; g(x) = 6x3/4
Answer:
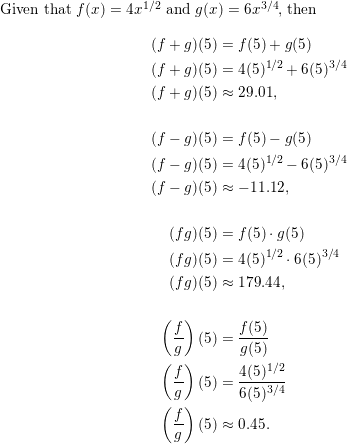
ERROR ANALYSIS In Exercises 17 and 18, describe and correct the error in stating the domain.
Question 17.
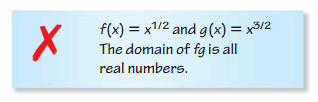
Answer:
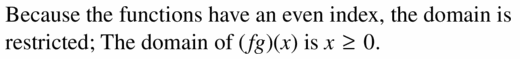
Question 18.

Answer:
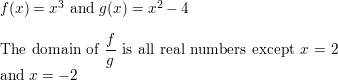
Question 19.
MODELING WITH MATHEMATICS From 1990 to 2010, the numbers (in millions) of female F and male M employees from the ages of 16 to 19 in the United States can be modeled by F(t) =−0.007t2 + 0.10t + 3.7 and M(t) = 0.0001t3 − 0.009t2 + 0.11t + 3.7, where t is the number of years since 1990.
a. Find (F + M)(t).
b. Explain what (F + M)(t) represents.
Answer:
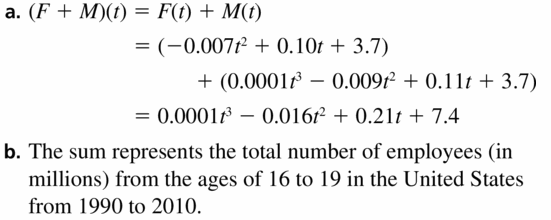
Question 20.
MODELING WITH MATHEMATICS From 2005 to 2009, the numbers of cruise ship departures (in thousands) from around the world W and Florida F can be modeled by the equations
W(t) = −5.8333t3 + 17.43t2 + 509.1t + 11496
F(t) = 12.5t3 − 60.29t2 + 136.6t + 4881
where t is the number of years since 2005.
a. Find (W − F )(t).
b. Explain what (W − F )(t) represents.
Answer:
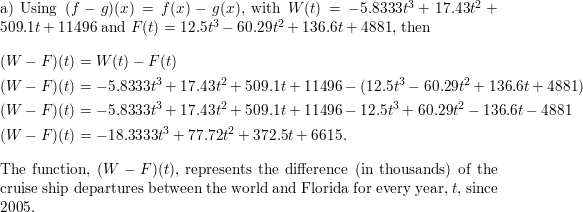
Question 21.
MAKING AN ARGUMENT Your friend claims that the addition of functions and the multiplication of functions are commutative. Is your friend correct? Explain your reasoning.
Answer:

Question 22.
HOW DO YOU SEE IT? The graphs of the functions f(x) = 3x2 − 2x − 1 and g(x) = 3x + 4 are shown. Which graph represents the function f + g? the function f − g? Explain your reasoning.
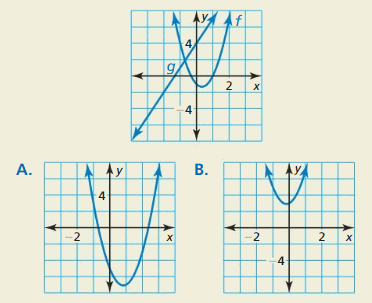
Answer:

Question 23.
REASONING The table shows the outputs of the two functions f and g. Use the table to evaluate (f + g)(3), (f − g)(1), (fg)(2), and (\(\frac{f}{g}\))(0).
Answer:
Question 24.
THOUGHT PROVOKING Is it possible to write two functions whose sum contains radicals, but whose product does not? Justify your answers.
Answer:
Question 25.
MATHEMATICAL CONNECTIONS A triangle is inscribed in a square, as shown. Write and simplify a function r in terms of x that represents the area of the shaded region.
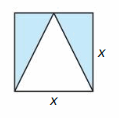
Answer:
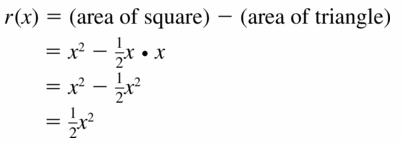
Question 26.
REWRITING A FORMULA For a mammal that weighs w grams, the volume b (in milliliters) of air breathed in and the volume d (in milliliters) of “dead space” (the portion of the lungs not filled with air) can be modeled by
b(w) = 0.007w and d(w) = 0.002w.
The breathing rate r (in breaths per minute) of a mammal that weighs w grams can be modeled by
r(w) = \(\frac{1.1 w^{0.734}}{b(w)-d(w)}\).
Answer:

Question 27.
PROBLEM SOLVING A mathematician at a lake throws a tennis ball from point A along the water’s edge to point B in the water, as shown. His dog, Elvis, first runs along the beach from point A to point D and then swims to fetch the ball at point B.
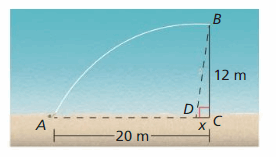
a. Elvis runs at a speed of about 6.4 meters per second. Write a function r in terms of x that represents the time he spends running from point A to point D. Elvis swims at a speed of about 0.9 meter per second. Write a function s in terms of x that represents the time he spends swimming from point D to point B.
b. Write a function t in terms of x that represents the total time Elvis spends traveling from point A to point D to point B.
c. Use a graphing calculator to graph t. Find the value of x that minimizes t. Explain the meaning of this value.
Answer:
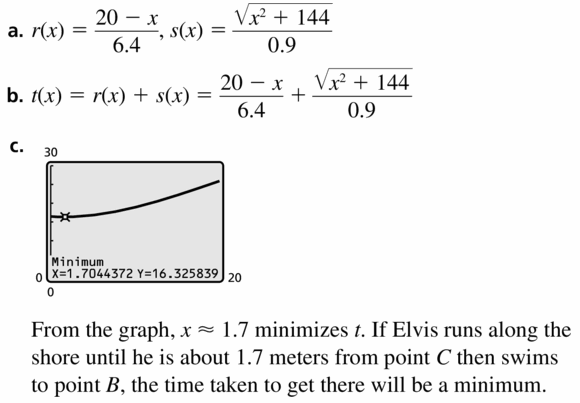
Maintaining Mathematical Proficiency
Solve the literal equation for n. (Skills Review Handbook)
Question 28.
3xn − 9 = 6y
Answer:
Given,
3xn − 9 = 6y
Take 3 as a common factor
xn – 3 = 2y
xn = 2y + 3
n = (2y + 3)/x
Question 29.
5z = 7n + 8nz
Answer:
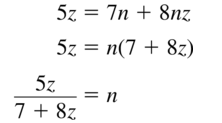
Question 30.
3nb = 5n − 6z
Answer:
Given,
3nb = 5n − 6z
3nb – 5n = -6z
Take n as the common factor to make n as the subject.
n(3b – 5) = -6z
n = -6z/(3b – 5)
Question 31.
\(\frac{3+4 n}{n}\) = 7b
Answer:
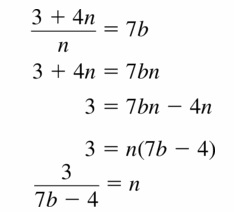
Determine whether the relation is a function. Explain. (Skills Review Handbook)
Question 32.
(3, 4), (4, 6), (1, 4), (2, −1)
Answer:
Question 33.
(−1, 2), (3, 7), (0, 2), (−1, −1)
Answer:
![]()
Question 34.
(1, 6), (7, −3), (4, 0), (3, 0)
Answer:

Question 35.
(3, 8), (2, 5), (9, 5), (2, −3)
Answer:
![]()
Lesson 5.6 Inverse of a Function
Essential Question
How can you sketch the graph of the inverse of a function?
EXPLORATION 1
Graphing Functions and Their Inverses
Work with a partner. Each pair of functions are inverses of each other. Use a graphing calculator to graph f and g in the same viewing window. What do you notice about the graphs?

a. f(x) = 4x + 3
g(x) = \(\frac{x-3}{4}\)
b. f(x) = x3 + 1
g(x) = \(\sqrt[3]{x-1}\)
c. f(x) = \(\sqrt{x-3}[latex]
g(x) = x2 + 3, x ≥ 0
d. f(x) = [latex]\frac{4 x+4}{x+5}\)
g(x) = \(\frac{4-5 x}{x-4}\)
EXPLORATION 2
Sketching Graphs of Inverse Functions
Work with a partner. Use the graph of f to sketch the graph of g, the inverse function of f, on the same set of coordinate axes. Explain your reasoning.
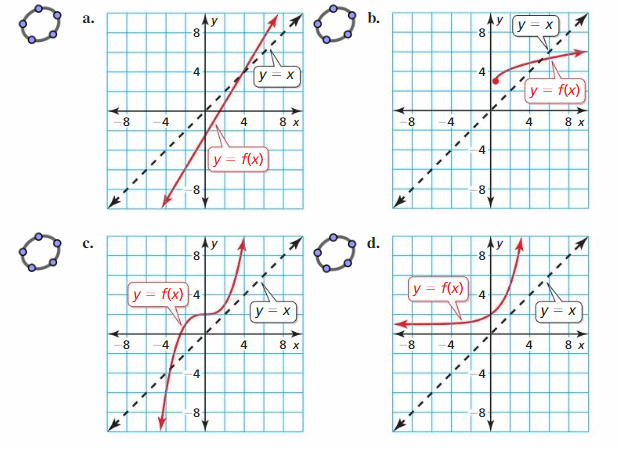
Communicate Your Answer
Question 3.
How can you sketch the graph of the inverse of a function?
Question 4.
In Exploration 1, what do you notice about the relationship between the equations of f and g? Use your answer to find g, the inverse function of
f(x) = 2x − 3.
Use a graph to check your answer.
5.6 Lesson
Monitoring Progress
Solve y = f(x) for x. Then find the input(s) when the output is 2.
Question 1.
f(x) = x − 2
Answer:
Given,
f(x) = x − 2
The values of x are the input values of the function.
f(x) = 2
If the output value of the function f is 2.
2 = x – 2
2 + 2 = x
x = 4
Question 2.
f(x) = 2x2
Answer:
f(x) = 2x²
The values of x are the input values of the function.
f(x) = 2
If the output value of the function f is 2.
2 = 2x²
x² = 1
x = ±1
Question 3.
f(x) = −x3 + 3
Answer:
Given,
f(x) = −x3 + 3
The values of x are the input values of the function.
f(x) = 2
If the output value of the function f is 2.
2 = -x³ + 3
-x³ = 3 – 2
-x³ = 1
-x = ±1
Find the inverse of the function. Then graph the function and its inverse.
Question 4.
f(x) = 2x
Question 5.
f(x) = −x + 1
Question 6.
f(x) = \(\frac{1}{3}\)x − 2
Find the inverse of the function. Then graph the function and its inverse.
Question 7.
f(x) = −x2, x ≤ 0
Question 8.
f(x) = −x3 + 4
Question 9.
f(x) = \(\sqrt{x+2}\)
Determine whether the functions are inverse functions.
Question 10.
f(x) = x + 5, g(x) = x − 5
Question 11.
f(x) = 8x3, g(x) = \(\sqrt[3]{2 x}\)
Question 12.
The distance d (in meters) that a dropped object falls in t seconds on Earth is represented by d = 4.9t2. Find the inverse of the function. How long does it take an object to fall 50 meters?
Inverse of a Function 5.6 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY In your own words, state the definition of inverse functions.
Answer:
![]()
Question 2.
WRITING Explain how to determine whether the inverse of a function is also a function.
Answer:
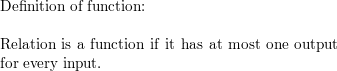
Question 3.
COMPLETE THE SENTENCE Functions f and g are inverses of each other provided that f(g(x)) = ____ and g(f(x)) = ____.
Answer:
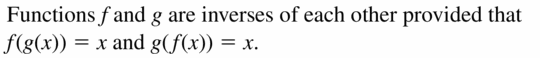
Question 4.
DIFFERENT WORDS, SAME QUESTION Which is different? Find “both” answers.

Answer:
Monitoring Progress and Modeling with Mathematics
In Exercises 5–12, solve y = f(x) for x. Then find the input(s) when the output is -3.
Question 5.
f(x) = 3x + 5
Answer:
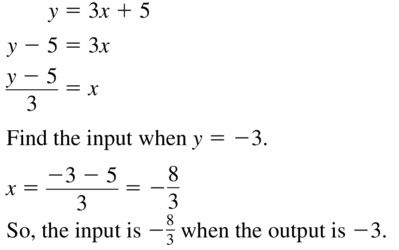
Question 6.
f(x) = −7x − 2
Answer:

Question 7.
f(x) = \(\frac{1}{2}\)x − 3
Answer:

Question 8.
f(x) = −\(\frac{2}{3}\)x + 1
Answer:
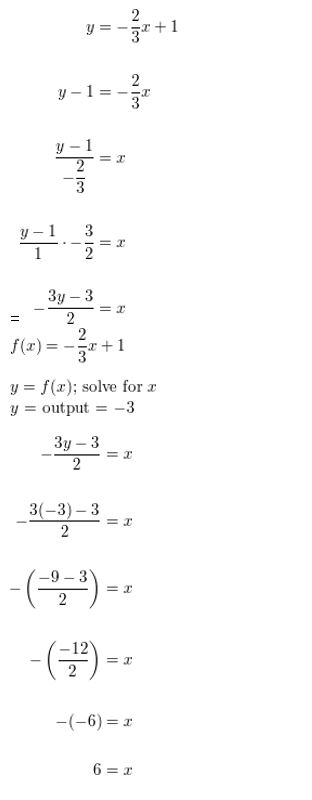
Question 9.
f(x) = 3x3
Answer:

Question 10.
f(x) = 2x4 − 5
Answer:
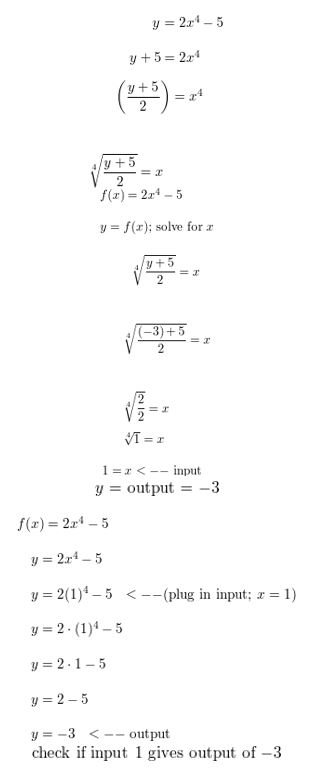
Question 11.
f(x) = (x − 2)2 − 7
Answer:
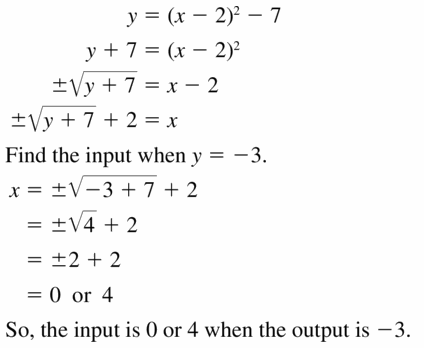
Question 12.
f(x) = (x − 5)3 − 1
Answer:
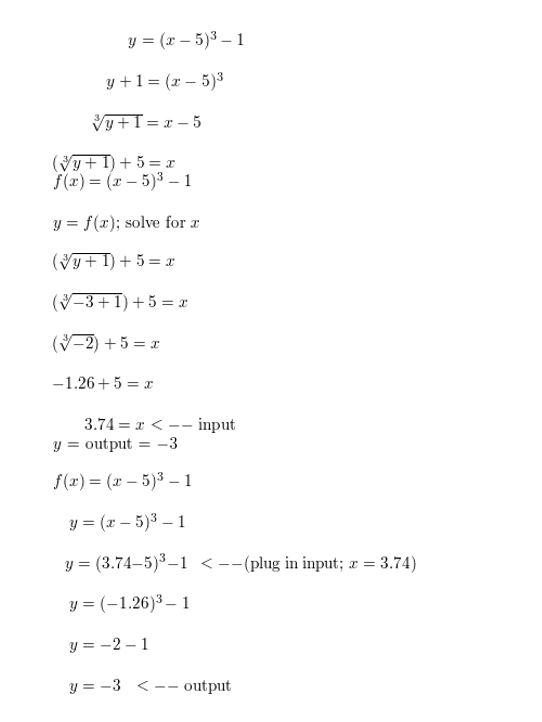
In Exercises 13–20, find the inverse of the function. Then graph the function and its inverse.
Question 13.
f(x) = 6x
Answer:

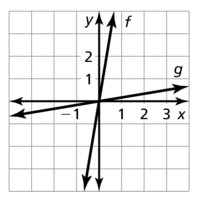
Question 14.
f(x) = −3x
Answer:
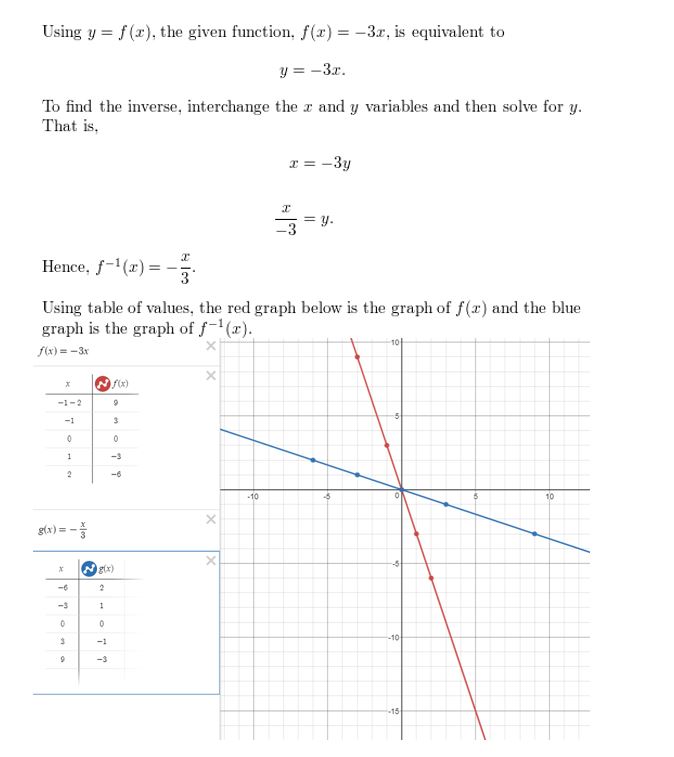
Question 15.
f(x) = −2x + 5
Answer:

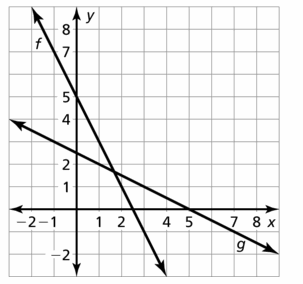
Question 16.
f(x) = 6x − 3
Answer:
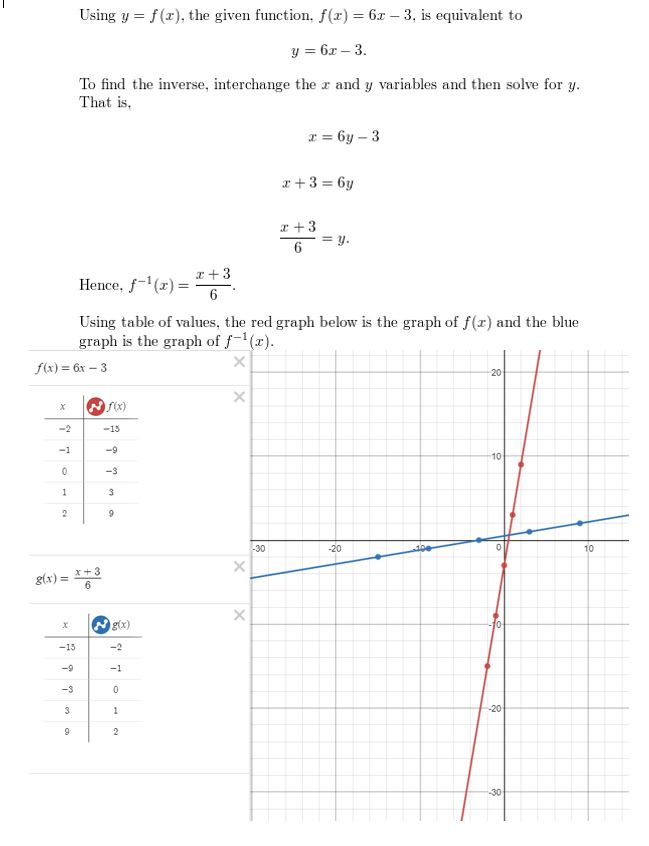
Question 17.
f(x) = −\(\frac{1}{2}\)x + 4
Answer:

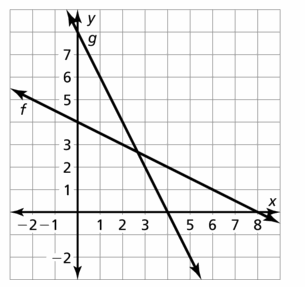
Question 18.
f(x) = \(\frac{1}{3}\)x − 1
Answer:
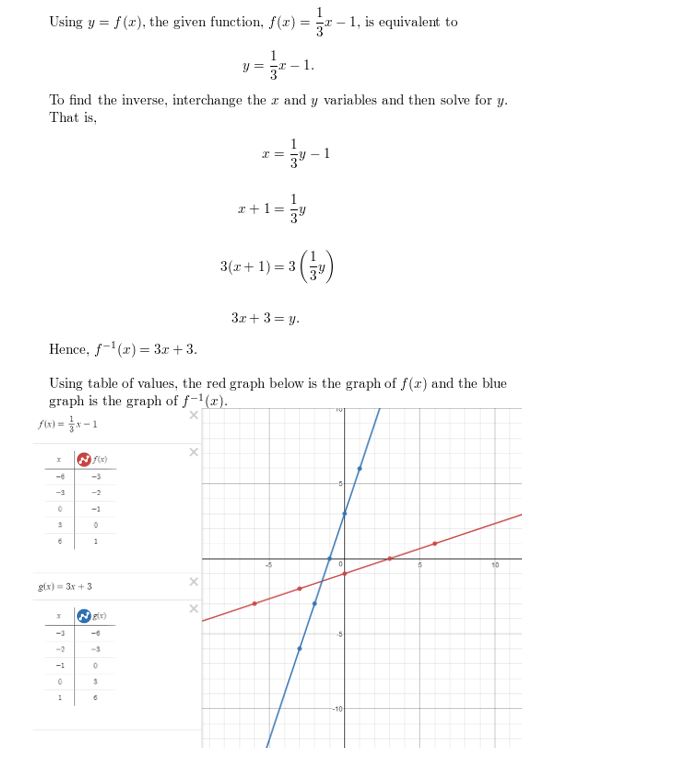
Question 19.
f(x) = \(\frac{2}{3}\)x − \(\frac{1}{3}\)
Answer:

Question 20.
f(x) = −\(\frac{4}{5}\)x + \(\frac{1}{5}\)
Answer:
Question 21.
COMPARING METHODS Find the inverse of the function f(x) = −3x + 4 by switching the roles of x and y and solving for y. Then find the inverse of the function f by using inverse operations in the reverse order. Which method do you prefer? Explain.
Answer:

Question 22.
REASONING Determine whether each pair of functions f and g are inverses. Explain your reasoning.
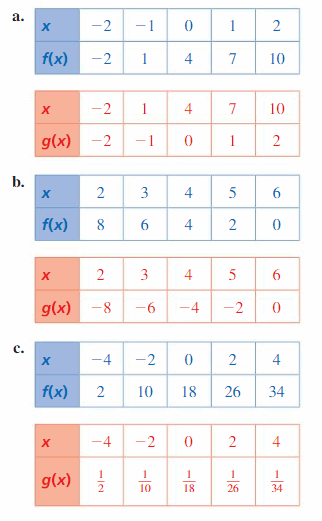
Answer:

In Exercises 23–28, find the inverse of the function. Then graph the function and its inverse.
Question 23.
f(x) = 4x2, x ≤ 0
Answer:
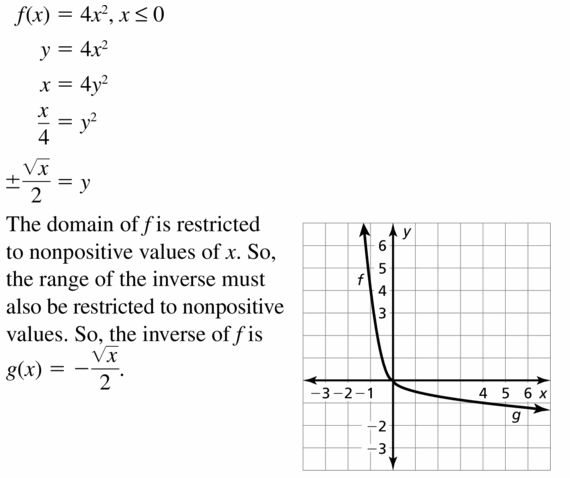
Question 24.
f(x) = 9x2, x ≤ 0
Answer:
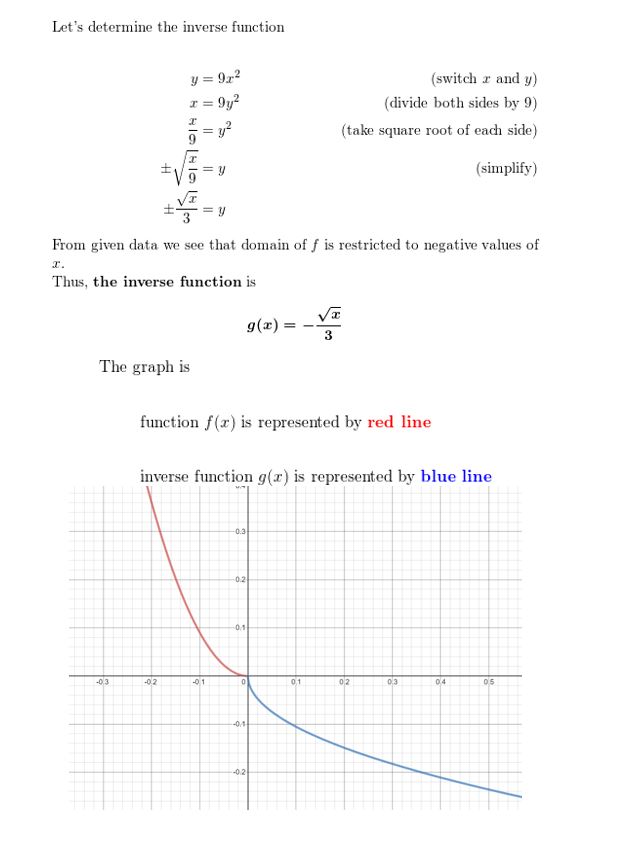
Question 25.
f(x) = (x − 3)3
Answer:
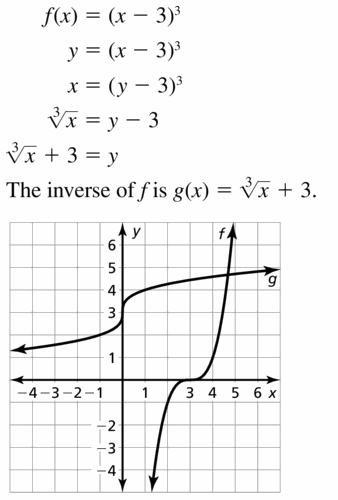
Question 26.
f(x) = (x + 4)3
Answer:
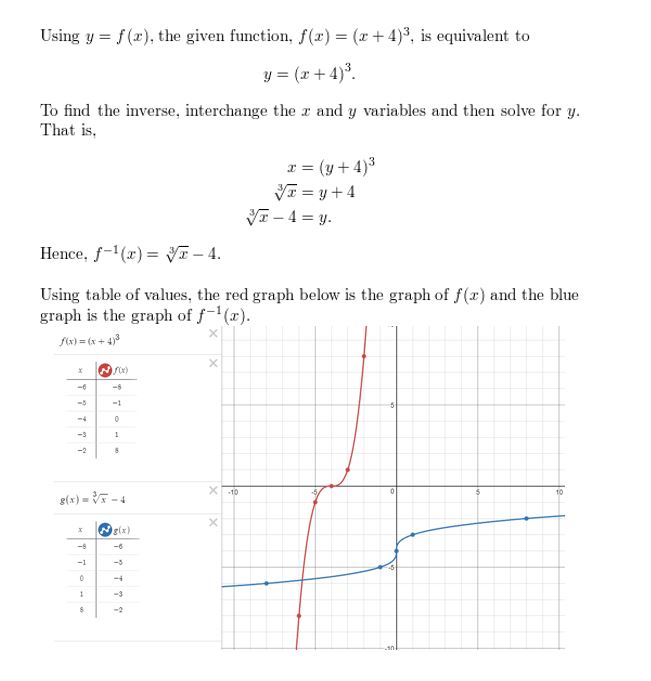
Question 27.
f(x) = 2x4, x ≥ 0
Answer:
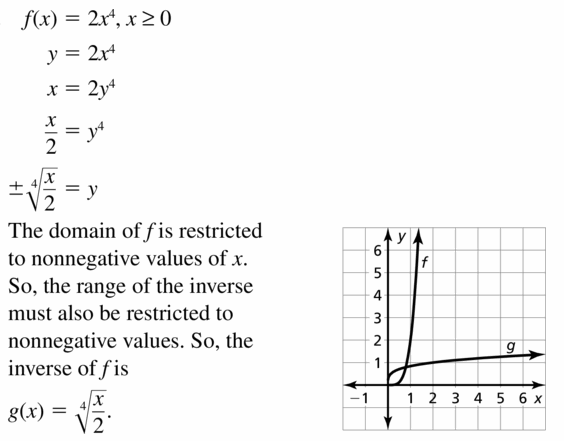
Question 28.
f(x) = −x6, x ≥ 0
Answer:
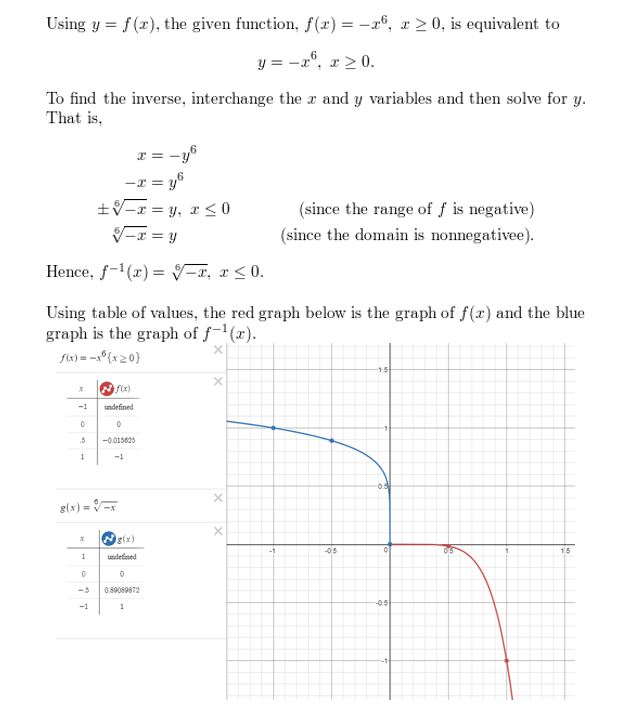
ERROR ANALYSIS In Exercises 29 and 30, describe and correct the error in finding the inverse of the function.
Question 29.
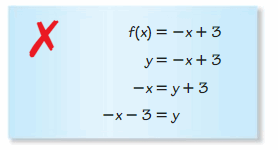
Answer:
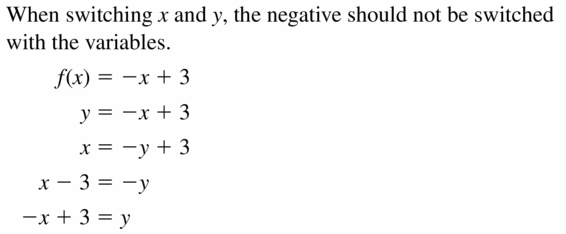
Question 30.
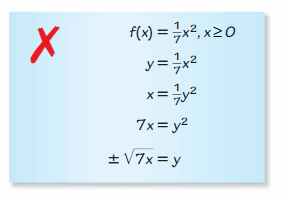
Answer:
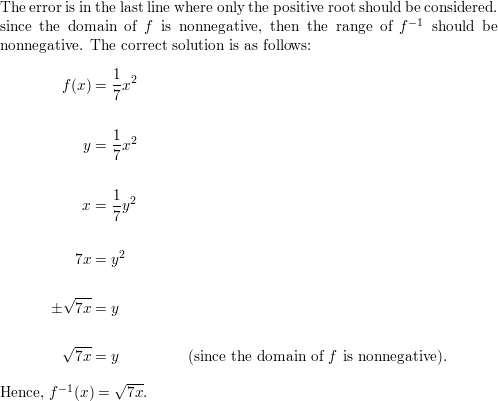
USING TOOLS In Exercises 31–34, use the graph to determine whether the inverse of f is a function. Explain your reasoning.
Question 31.
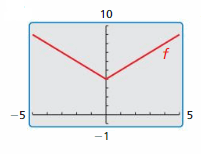
Answer:

Question 32.
Answer:
As per the horizontal line test, the horizontal line intersects the graph more than once. f foes do not have the inverse function. therefore the inverse of the function is not a function.
Question 33.
Answer:

Question 34.
Answer:
As per the horizontal line test, the horizontal line intersects the graph only once, thus the inverse of the function is a function.
In Exercises 35–46, determine whether the inverse of f is a function. Then find the inverse.
Question 35.
f(x) = x3 − 1
Answer:
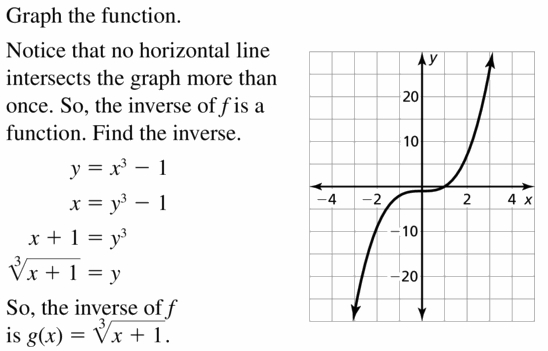
Question 36.
f(x) = −x3 + 3
Answer:
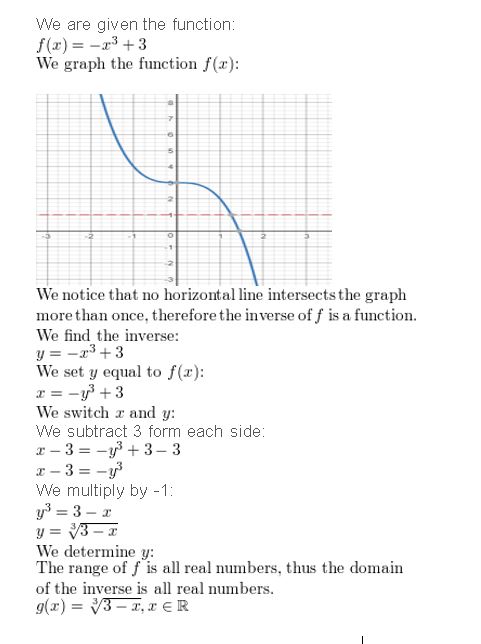
Question 37.
f(x) = \(\sqrt{x+4}\)
Answer:
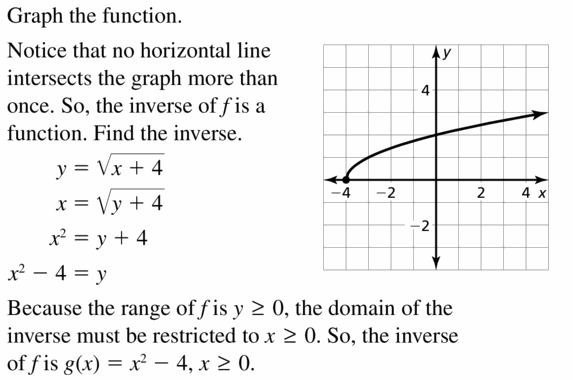
Question 38.
f(x) = \(\sqrt{x-6}\)
Answer:
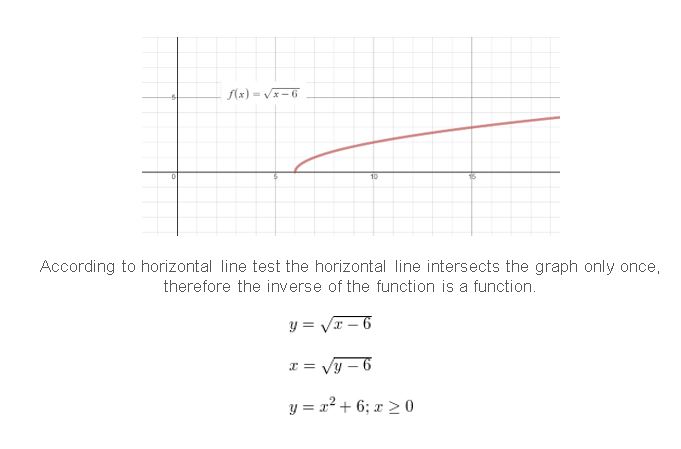
Question 39.
f(x) = \(2 \sqrt[3]{x-5}\)
Answer:
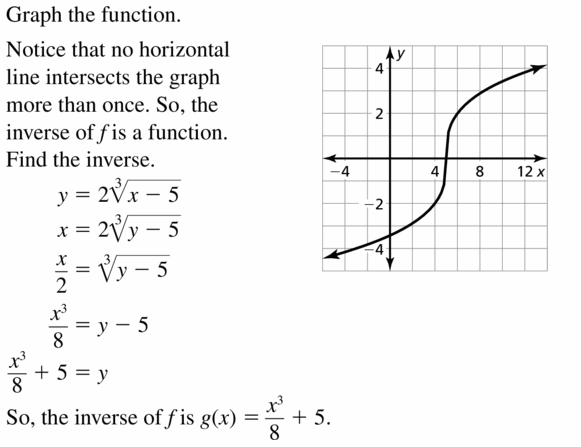
Question 40.
f(x) = 2x2 − 5
Answer:
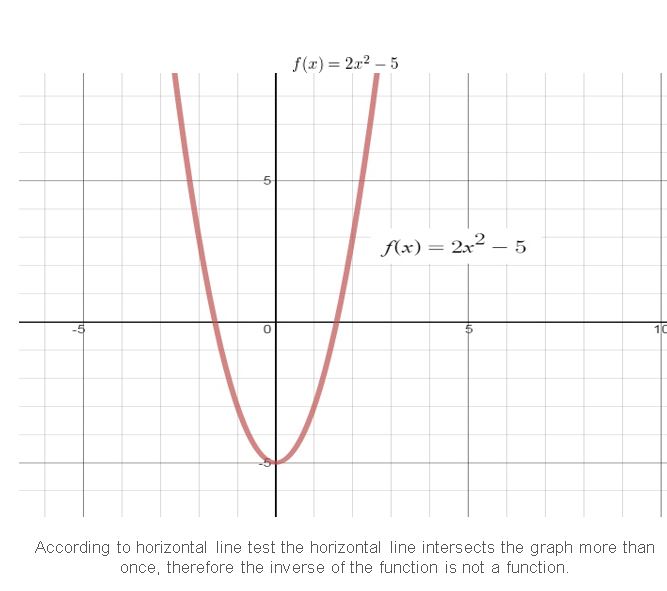
Question 41.
f(x) = x4 + 2
Answer:
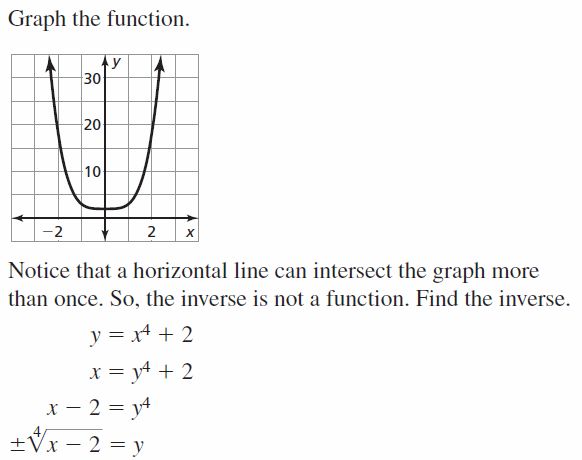
Question 42.
f(x) = 2x3 − 5
Answer:
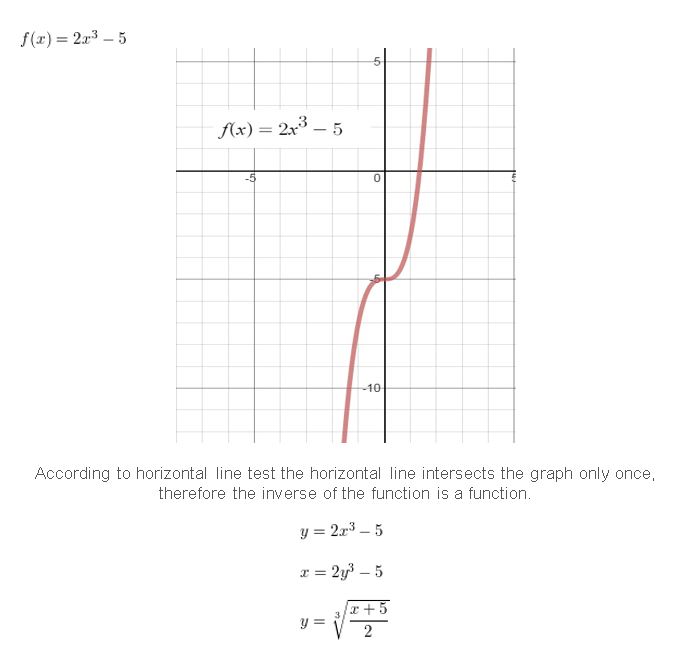
Question 43.
f(x) = \(3 \sqrt[3]{x+1}\)
Answer:
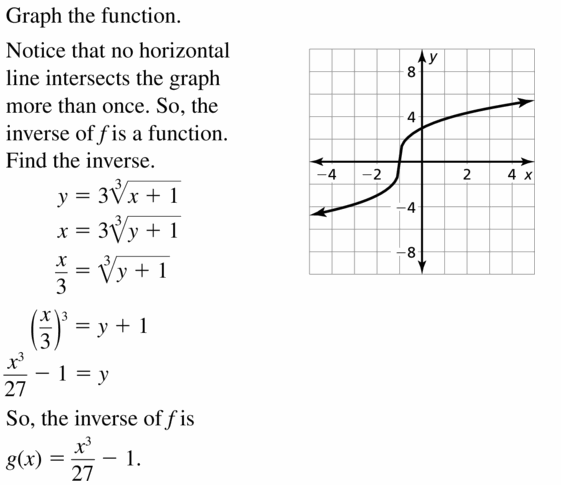
Question 44.
f(x) = \(-\sqrt[3]{\frac{2 x+4}{3}}\)
Answer:
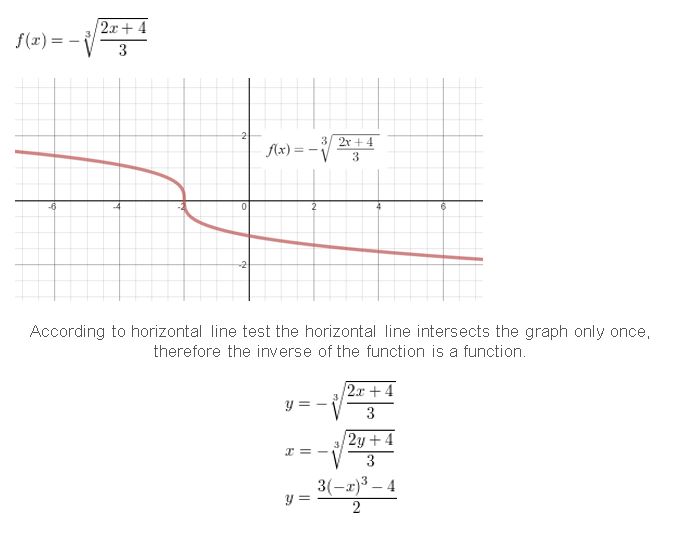
Question 45.
f(x) = \(\frac{1}{2}\)x5
Answer:
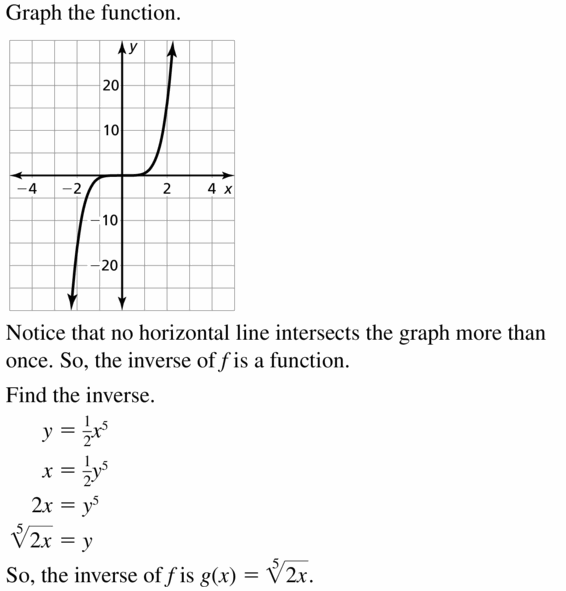
Question 46.
f(x) = \(-3 \sqrt{\frac{4 x-7}{3}}\)
Answer:
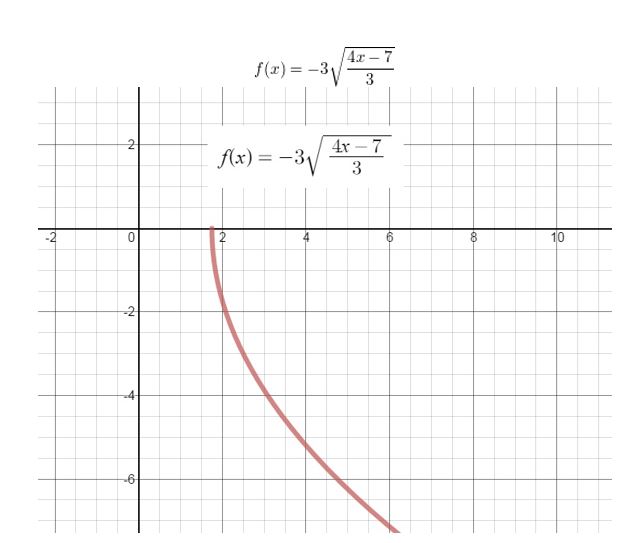
Question 47.
WRITING EQUATIONS What is the inverse of the function whose graph is shown?
A. g(x) = \(\frac{3}{2}\)x − 6
B. g(x) = \(\frac{3}{2}\)x + 6
C. g(x) = \(\frac{2}{3}\)x − 6
D. g(x) = \(\frac{2}{3}\)x + 12
Answer:
![]()
Question 48.
WRITING EQUATIONS What is the inverse of f(x) = −\(-\frac{1}{64}\)x3?
A. g(x) = −4x3
B. g(x) = 4\(\sqrt[3]{x}\)
C. g(x) = −4\(\sqrt[3]{x}\)
D. g(x) = \(\sqrt[3]{-4 x}\)
Answer:
In Exercises 49–52, determine whether the functions are inverses.
Question 49.
f(x) = 2x − 9, g(x) = x — 2 + 9
Answer:

Question 50.
f(x) = \(\frac{x-3}{4}\), g(x) = 4x + 3
Answer:
Question 51.
f(x) = \(\sqrt[5]{\frac{x+9}{5}}\), g(x) = 5x5 − 9
Answer:
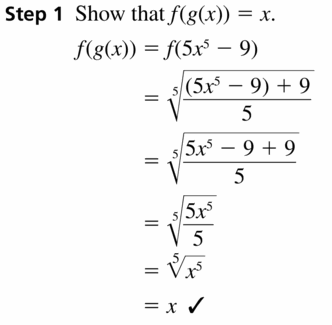

Question 52.
f(x) = 7x3/2 − 4, g(x) = (\(\frac{x+4}{7}\))3/2
Answer:
Question 53.
MODELING WITH MATHEMATICS The maximum hull speed v (in knots) of a boat with a displacement hull can be approximated by v = 1.34\(\sqrt{\ell}\), where ℓ is the waterline length (in feet) of the boat. Find the inverse function. What waterline length is needed to achieve a maximum speed of 7.5 knots?

Answer:

Question 54.
MODELING WITH MATHEMATICS Elastic bands can be used for exercising to provide a range of resistance. The resistance R (in pounds) of a band can be modeled by R = \(\frac{3}{8}\)L − 5, where L is the total length (in inches) of the stretched band. Find the inverse function. What length of the stretched band provides 19 pounds of resistance?
Answer:
ANALYZING RELATIONSHIPS In Exercises 55–58, match the graph of the function with the graph of its inverse.
Question 55.
Answer:
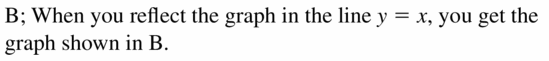
Question 56.
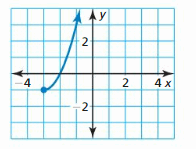
Answer:

Question 57.
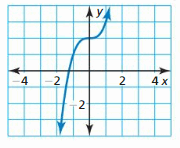
Answer:
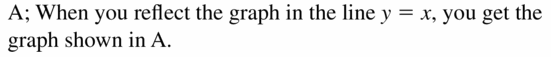
Question 58.
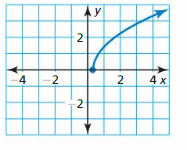
Answer:
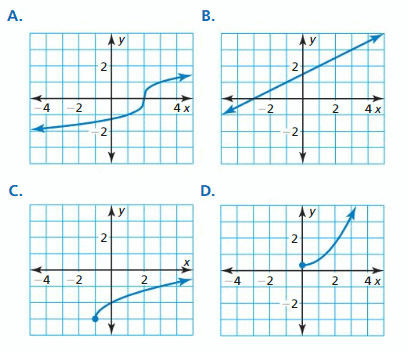
Question 59.
REASONING You and a friend are playing a number-guessing game. You ask your friend to think of a positive number, square the number, multiply the result by 2, and then add 3. Your friend’s final answer is 53. What was the original number chosen? Justify your answer.
Answer:

Question 60.
MAKING AN ARGUMENT Your friend claims that every quadratic function whose domain is restricted to nonnegative values has an inverse function. Is your friend correct? Explain your reasoning.
Answer:
Question 61.
PROBLEM SOLVING When calibrating a spring scale, you need to know how far the spring stretches for various weights. Hooke’s Law states that the length a spring stretches is proportional to the weight attached to it. A model for one scale is ℓ = 0.5w + 3, whereℓ is the total length (in inches) of the stretched spring and w is the weight (in pounds) of the object.
a. Find the inverse function. Describe what it represents.
b. You place a melon on the scale, and the spring stretches to a total length of 5.5 inches. Determine the weight of the melon.
c. Verify that the function ℓ = 0.5w + 3 and the inverse model in part (a) are inverse functions.
Answer:

Question 62.
THOUGHT PROVOKING Do functions of the form y = xm/n, where m and n are positive integers, have inverse functions? Justify your answer with examples.
Answer:

Question 63.
PROBLEM SOLVING At the start of a dog sled race in Anchorage, Alaska, the temperature was 5°C. By the end of the race, the temperature was −10°C. The formula for converting temperatures from degrees Fahrenheit F to degrees Celsius C is C = \(\frac{5}{9}\)(F − 32).
a. Find the inverse function. Describe what it represents.
b. Find the Fahrenheit temperatures at the start and end of the race.

c. Use a graphing calculator to graph the original function and its inverse. Find the temperature that is the same on both temperature scales.
Answer:
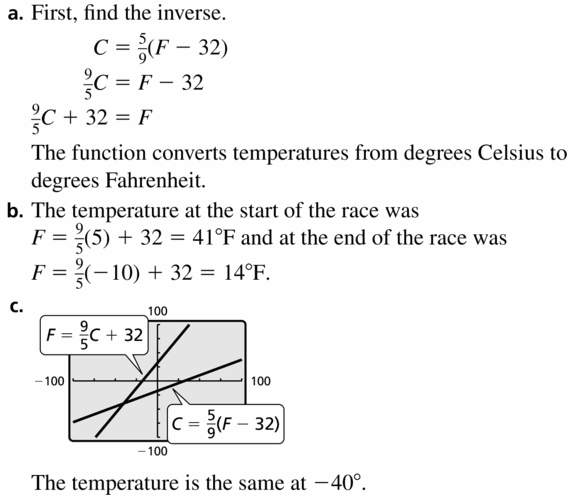
Question 64.
PROBLEM SOLVING The surface area A (in square meters) of a person with a mass of 60 kilograms can be approximated by A = 0.2195h0.3964, where h is the height (in centimeters) of the person.
a. Find the inverse function. Then estimate the height of a 60-kilogram person who has a body surface area of 1.6 square meters.
b. Verify that function A and the inverse model in part (a) are inverse functions.
Answer:
USING STRUCTURE In Exercises 65–68, match the function with the graph of its inverse.
Question 65.
f(x) = \(\sqrt[3]{x-4}\)
Answer:
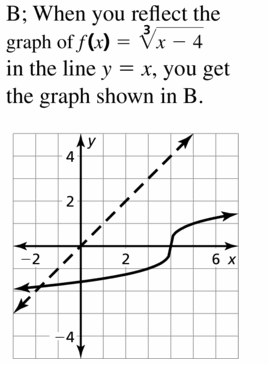
Question 66.
f(x) = \(\sqrt[3]{x+4}\)
Answer:
Question 67.
f(x) = \(\sqrt{x+1}\) – 3
Answer:
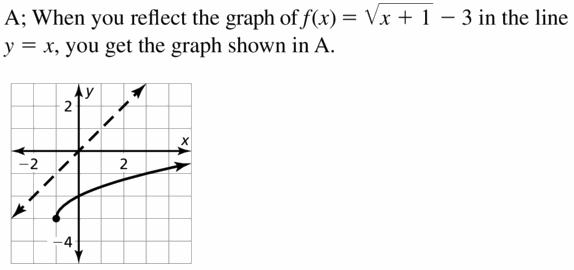
Question 68.
f(x) = \(\sqrt{x-1}\) + 3
Answer:
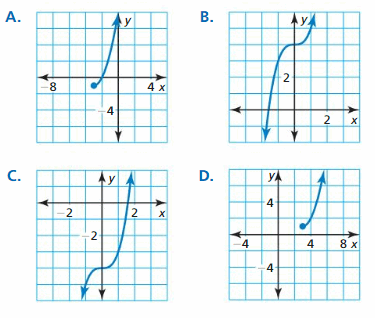
Question 69.
DRAWING CONCLUSIONS Determine whether the statement is true or false. Explain your reasoning.
a. If f(x) = xn and n is a positive even integer, then the inverse of f is a function.
b. If f(x) = xn and n is a positive odd integer, then the inverse of f is a function.
Answer:

Question 70.
HOW DO YOU SEE IT? The graph of the function f is shown. Name three points that lie on the graph of the inverse of f. Explain your reasoning.
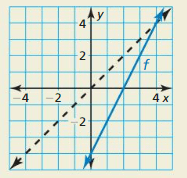
Answer:
Question 71.
ABSTRACT REASONING Show that the inverse of any linear function f(x) = mx + b, where m ≠ 0, is also a linear function. Identify the slope and y-intercept of the graph of the inverse function in terms of m and b.
Answer:
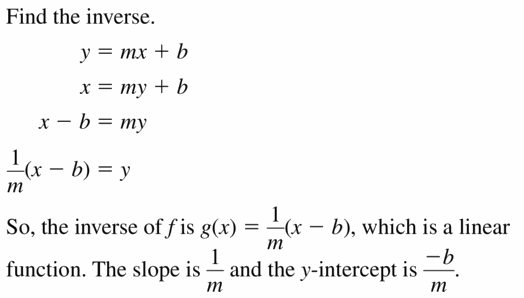
Question 72.
CRITICAL THINKING Consider the function f(x) = −x.
a. Graph f(x) = −x and explain why it is its own inverse. Also, verify that f(x) = −x is its own inverse algebraically.
b. Graph other linear functions that are their own inverses. Write equations of the lines you graphed.
c. Use your results from part (b) to write a general equation describing the family of linear functions that are their own inverses.
Answer:
Maintaining Mathematical Proficiency
Simplify the expression. Write your answer using only positive exponents.(Skills Review Handbook)
Question 73.
(−3)−3
Answer:
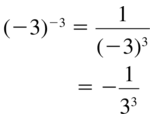
Question 74.
23 • 22
Answer:
Given
23 • 22
When bases are equal powers should be added.
23+2 = 25
Question 75.
\(\frac{4^{5}}{4^{3}}\)
Answer:
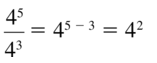
Question 76.
(\(\frac{2}{3}\))4
Answer:
Given,
(\(\frac{2}{3}\))4
(\(\frac{a}{b}\))n= an/bn
= 24/34
= 16/81
Describe the x-values for which the function is increasing, decreasing, positive, and negative.
Question 77.
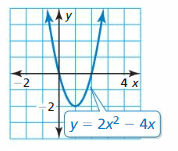
Answer:
Question 78.
Answer:
Question 79.
Answer:
Rational Exponents and Radical Functions Performance Task: Turning the Tables
5.4–5.6 What Did You Learn?
Core Vocabulary
radical equation, p. 262
extraneous solutions, p. 263
inverse functions, p. 277
Core Concepts
Section 5.4
Solving Radical Equations, p. 262
Solving Radical Inequalities, p. 265
Section 5.5
Operations on Functions, p. 270
Section 5.6
Exploring Inverses of Functions, p. 276
Inverses of Nonlinear Functions, p. 278
Horizontal Line Test, p. 278
Mathematical Practices
Question 1.
How did you find the endpoints of the range in part (b) of Exercise 54 on page 267?
Question 2.
How did you use structure in Exercise 57 on page 268?
Question 3.
How can you evaluate the reasonableness of the results in Exercise 27 on page 274?
Question 4.
How can you use a graphing calculator to check your answers in Exercises 49–52 on page 282?
Performance Task
Turning the Tables
In this chapter, you have used properties of rational exponents and functions to find an answer to the problem. Using those same properties, can you find a problem to the answer? How many problems can you find?

To explore the answers to these questions and more, go to BigIdeasMath.com
Rational Exponents and Radical Functions Chapter Review
Evaluate the expression without using a calculator.
Question 1.
87/3
Answer:
Given,
87/3
We can write the given radical as
87 . 81/3
= 2097152 × 2
= 4194304
So, 87/3 = 4194304
Question 2.
95/2
Answer:
Given,
95/2
We can write the given radical as
95 × 91/2
= 59049 × 3
= 177147
So, 95/2 = 177147
Question 3.
(−27)−2/3
Answer:
Given,
(-27)−2 × (-27)1/3
= -3 × √27
Find the real solution(s) of the equation. Round your answer to two decimal places when appropriate.
Question 4.
x5 + 17 = 35
Answer:
Given,
x5 + 17 = 35
x5 = 35 – 17
x5 = 18
Applying the fifth root on both sides
x = 1.79
Question 5.
7x3 = 189
Answer:
Given,
7x3 = 189
x3 = 189/7
x3 = 27
Cubing on both sides
x = 3
Question 6.
(x + 8)4 = 16
Answer:
Given,
(x + 8)4 = 16
16 can be written as 24
(x + 8)4 = 24
x + 8 = 2
x = 2 – 8
x = -6
Simplify the expression.
Question 7.
(\(\frac{6^{1 / 5}}{6^{2 / 5}}\))3
Answer:
(\(\frac{6^{1 / 5}}{6^{2 / 5}}\))³
(\(\frac{6^{3 / 5}}{6^{6 / 5}}\))
Question 8.
\(\sqrt[4]{32} \cdot \sqrt[4]{8}\)
Answer:
Given,
\(\sqrt[4]{32} \cdot \sqrt[4]{8}\)
= \(\sqrt[4]{32×8}\)
= \(\sqrt[4]{256}\)
= \(\sqrt[4]{4^4}\)
= 4
Question 9.
\(\frac{1}{2-\sqrt[4]{9}}\)
Answer:
\(\frac{1}{2-\sqrt[4]{9}}\)
\(\sqrt[2]{9}\) = 1.73
= 1/(2 – 1.73)
= 1/0.27
= 3.7
Question 10.
\(4 \sqrt[5]{8}\) + \(3 \sqrt[5]{8}\)
Answer:
Given,
\(4 \sqrt[5]{8}\) + \(3 \sqrt[5]{8}\)
= \(\sqrt[5]{8}\)(4 + 3)
= 7\(\sqrt[5]{8}\)
So, \(4 \sqrt[5]{8}\) + \(3 \sqrt[5]{8}\) = 7\(\sqrt[5]{8}\)
Question 11.
\(2 \sqrt{48}\) – \(\sqrt{3}\)
Answer:
Given,
\(2 \sqrt{48}\) – \(\sqrt{3}\)
48 = 16 × 3
\(2 \sqrt{16×3}\) – \(\sqrt{3}\)
2 × 4 \(\sqrt{3}\) – \(\sqrt{3}\)
\(\sqrt{3}\)(8 – 1)
= 7\(\sqrt{3}\)
\(2 \sqrt{48}\) – \(\sqrt{3}\) = 7\(\sqrt{3}\)
Question 12.
(\(5^{2 / 3} \cdot 2^{3 / 2}\))1/2
Answer:
Given,
(5^2/3)1/2 × (2^3/2)1/2
=51/3 × 23/4
= \(\sqrt[3]{5}\) . \(\sqrt[4]{8}\)
= 2\(\sqrt[3]{5}\) . \(\sqrt[2]{2}\)
So, (\(5^{2 / 3} \cdot 2^{3 / 2}\))1/2 =2\(\sqrt[3]{5}\) . \(\sqrt[2]{2}\)
Simplify the expression. Assume all variables are positive.
Question 13.
\(\sqrt[3]{125 z^{9}}\)
Question 14.
\(\frac{2^{1 / 4} z^{5 / 4}}{6 z}\)
Question 15.
\(\sqrt{10 z^{5}}-z^{2} \sqrt{40 z}\)
Describe the transformation of f represented by g. Then graph each function.
Question 16.
f(x) = \(\sqrt{x}\), g(x) = −2\(\sqrt{x}\)
Question 17.
f(x) = \(\sqrt[3]{x}\), g(x) = \(\sqrt[3]{-x}\) − 6
Question 18.
Let the graph of g be a reflection in the y-axis, followed by a translation 7 units to the right of the graph of f(x) = \(\sqrt[3]{x}\). Write a rule for g.
Question 19.
Use a graphing calculator to graph 2y2 = x − 8. Identify the vertex and the direction that the parabola opens.
Question 20.
Use a graphing calculator to graph x2 + y2 = 81. Identify the radius and the intercepts.
Solve the equation. Check your solution.
Question 21.
\(4 \sqrt[3]{2 x+1}\) = 20
Question 22.
\(\sqrt{4 x-4}\) = \(\sqrt{5 x-1}\) – 1
Question 23.
(6x)2/3 = 36
Solve the inequality.
Question 24.
\(5 \sqrt{x}\) + 2 > 17
Question 25.
\(2 \sqrt{x-8}\) < 24
Question 26.
7\(\sqrt[3]{x-3}\) ≥ 21
Question 27.
In a tsunami, the wave speeds (in meters per second) can be modeled by s(d ) = \(\sqrt{9.8 d}\), where d is the depth (in meters) of the water. Estimate the depth of the water when the wave speed is 200 meters per second.
Question 28.
Let f(x) = 2\(\sqrt{3-x}\) and g(x) = 4\(\sqrt[3]{3-x}\). Find (fg)(x) and (\(\frac{f}{g}\))(x) and state the domain of each. Then evaluate(fg)(2) and (\(\frac{f}{g}\))(2).
Question 29.
Let f(x) = 3x2 + 1 and g(x) = x + 4. Find (f + g)(x) and (f − g)(x) and state the domain of each. Then evaluate (f + g)(−5) and (f − g)(−5).
Question 30.
f(x) = −\(\frac{1}{2}\)x + 10
Question 31.
f(x) = x2 + 8, x ≥ 0
Question 32.
f(x) = −x3 − 9
Question 33.
f(x) = 3\(\sqrt{x}\) + 5
Determine whether the functions are inverse functions.
Question 34.
f(x) = 4(x − 11)2, g(x) = \(\frac{1}{4}\)(x + 11)2
Question 35.
f(x) = −2x + 6, g(x) = −\(\frac{1}{2}\)x + 3
Question 36.
On a certain day, the function that gives U.S. dollars in terms of British pounds is d = 1.587p, where d represents U.S. dollars and p represents British pounds. Find the inverse function. Then find the number of British pounds equivalent to 100 U.S. dollars.
Rational Exponents and Radical Functions Chapter Test
Question 1.
Solve the inequality \(\) − 2 ≤ 13 and the equation 5\(\) − 2 = 13. Describe the similarities and differences in solving radical equations and radical inequalities.
Describe the transformation of f represented by g. Then write a rule for g.
Question 2.
f(x) = \(\sqrt{x}\)
Question 3.
f(x) = \(\sqrt[3]{x}\)
Question 4.
f(x) = \(\sqrt[5]{x}\)
Simplify the expression. Explain your reasoning.
Question 5.
642/3
Question 6.
(−27)5/3
Question 7.
\(\sqrt[4]{48 x y^{11} z^{3}}\)
Question 8.
\(\frac{\sqrt[3]{256}}{\sqrt[3]{32}}\)
Question 9.
Write two functions whose graphs are translations of the graph of y = \(\sqrt{x}\). The first function should have a domain of x ≥ 4. The second function should have a range of y ≥ −2.
Question 10.
In bowling, a handicap is a change in score to adjust for differences in the abilities of players. You belong to a bowling league in which your handicap h is determined using the formula h = 0.9(200 − a), where a is your average score. Find the inverse of the model. Then find the average for a bowler whose handicap is 36.
Question 11.
The basal metabolic rate of an animal is a measure of the amount of calories burned at rest for basic functioning. Kleiber’s law states that an animal’s basal metabolic rate R (in kilocalories per day) can be modeled by R = 73.3w3/4, where w is the mass (in kilograms) of the animal. Find the basal metabolic rates of each animal in the table.
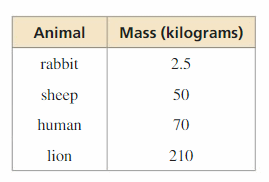
Question 12.
Let f(x) = 6x3/5 and g(x) = −x3/5. Find (f + g)(x) and (f − g)(x) and state the domain of each. Then evaluate (f + g)(32) and (f − g)(32).
Question 13.
Let f(x) = \(\frac{1}{2}\)x3/4 and g(x) = 8x. Find (fg)(x) and (\(\frac{f}{g}\))(x) and state the domain of each. Then evaluate (fg)(16) and (\(\frac{f}{g}\))(16).
Question 14.
A football player jumps to catch a pass. The maximum height h (in feet) of the player above the ground is given by the function h = \(\frac{1}{64}\)s2, where s is the initial speed (in feet per second) of the player. Find the inverse of the function. Use the inverse to find the initial speed of the player shown. Verify that the functions are inverse functions.

Rational Exponents and Radical Functions Cumulative Assessment
Question 1.
Identify three pairs of equivalent expressions. Assume all variables are positive. Justify your answer.
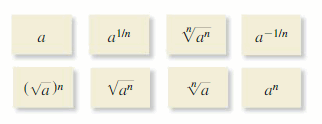
Question 2.
The graph represents the function ![]() . Choose the correct values to complete the function.
. Choose the correct values to complete the function.
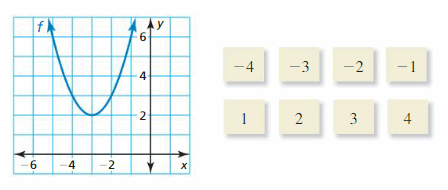
Question 3.
In rowing, the boat speed s (in meters per second) can be modeled by s= 4.62\(\sqrt[9]{n}\), where n is the number of rowers.
a. Find the boat speeds for crews of 2 people, 4 people, and 8 people.
b. Does the boat speed double when the number of rowers doubles? Explain.
c. Find the time (in minutes) it takes each crew in part (a) to complete a 2000-meter race.
Question 4.
A polynomial function fits the data in the table. Use finite differences to find the degree of the function and complete the table. Explain your reasoning.

Question 5.
The area of the triangle is 42 square inches. Find the value of x.
Answer:
Given,
The area of the triangle is 42 square inches.
b = (x + 8)
h = x
We know that,
Area of the triangle = 1/2 × b × h
A = 42
42 = 1/2 × (x + 8) × x
84 = x² + 8x
x² + 8x – 84 = 0
Question 6.
Which equations are represented by parabolas? Which equations are functions? Place check marks in the appropriate spaces. Explain your reasoning.
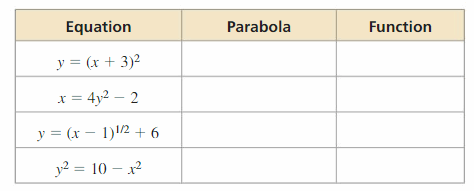
Question 7.
What is the solution of the inequality 2\(\sqrt{x+3}\) − 1 < 3?
A. x < 1
B. −3 < x < 1
C. −3 ≤ x < 1
D. x ≥ −3
Question 8.
Which function does the graph represent? Explain your reasoning.
Question 9.
Your friend releases a weather balloon 50 feet from you. The balloon rises vertically. When the balloon is at height h, the distance d between you and the balloon is given by d = \(\sqrt{2500+h^{2}}\), where h and d are measured in feet. Find the inverse of the function. What is the height of the balloon when the distance between you and the balloon is 100 feet?
Question 10.
The graphs of two functions f and g are shown. Are f and g inverse functions? Explain your reasoning.