Big Ideas Math Book 5th Grade Answer Key Chapter 2 Numerical Expressions helps the students who are willing to be perfect in their Math skills and also to helps the parents guiding their children to get a good score in examinations. In this chapter numerical expressions, one can download this pdf for free of cost. And in this chapter, each and every question was explained in detail which helps students to understand easily. Get started to stop those hurdling times to studying hard to grasping the solutions by learning these methods of solving modern math problems in an effective way. This chapter Big Ideas Math Answers Grade 5 Chapter 2 Numerical Expressions explains various types of questions.
Big Ideas Math Book 5th Grade Answer Key Chapter 2 Numerical Expressions
In this chapter, we can see different topics on Numerical Expressions, Number properties, Order of operations, Evaluating numerical expressions, and practice questions. Those topics were being set up by the mathematical professionals as indicated by the most recent release. Look down this page to get the answers to all the inquiries. Click on the links to look at the subjects shrouded in this chapter Numerical Expressions.
Lesson 1 Number Properties
Lesson 2 Order of Operations
Lesson 3 Write Numerical Expressions
Lesson 4 Evaluate Expressions with Grouping Symbols
- Lesson 2.4 Evaluate Expressions with Grouping Symbols
- Evaluate Expressions with Grouping Symbols Homework & Practice 2.4
Performance Task
- Numerical Expressions Performance Task
- Numerical Expressions Activity
- Numerical Expressions Chapter Practice
Lesson 2.1 Number Properties
Explore and Grow
Use all four numbers on the game card below to write an expression that has a value of 24. You can use any number of the four operations: addition, subtraction, multiplication, and division.
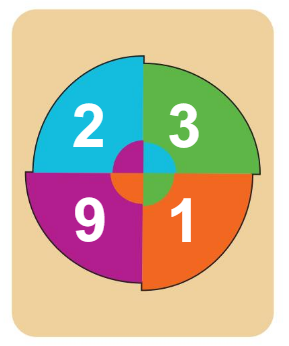
Answer:
We will use addition, multiplication, and division to get the value as 24.
Explanation:
In the game card, we can see that the four numbers are 2, 3, 9, 1. So to get the value as 24 we will add 9 + 3 which is 12 and then we will multiply the value 12 with 2 which is 12 × 2 = 24 and then we will divide the value with 1 which is 24 ÷ 1= 24. So here the operations used are addition, multiplication, and division to get the value 24.
Reasoning
Write another expression that has a value of 24 using the game card above.
Answer:
We will use addition and multiplication to get the value as 24.
Explanation:
In the game card, we can see that the four numbers are 2, 3, 9, 1. So to get the value as 24 we will add 9 + 3 which is 12 and then we will multiply the value 12 with 2 which is 12 × 2 = 24. So to use another expression we will multiply the value with 1 which is 24 × 1= 24. So here the operations used are addition and multiplication to get the value 24.
Think and Grow: Use Number Properties
Key Idea
Here are several number properties.
Commutative Properties: Changing the order of addends or factors does not change the sum or product.
3 + 5 = 5 + 3
3 × 5 = 5 × 3
Associative Properties: Changing the grouping of addends or factors does not change the sum or product.
(2 + 4) + 1 = 2 + (4 + 1)
(2 × 4) × 1 = 2 × (4 × 1)
Addition Property of Zero: The sum of any number and 0 is that number.
8 + 0 = 8
Multiplication Properties of Zero and One:
The product of any number and 0 is 0. 5 × 0 = 0
The product of any number and 1 is that number. 7 × 1 = 7
Distributive Property: Multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products.
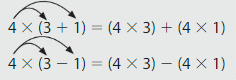
Example
Complete the equation. Identify the property shown.
32 + 29 + 8 = 29 + ______ + 8
_______ Property of Addition

Show and Grow
Question 1.
Complete the equation. Identify the property shown.
9 × 15 = 15 × ______
Answer:
The equation is 9 × 15 = 15 × 9. And the property which is used is the Commutative property.
Explanation:
The equation is 9 × 15 = 15 × 9. And the property which is used is the Commutative property.
Commutative Properties means changing the order of addends or factors does not change the sum or product. So the equation is 9 × 15 = 15 × 9.
Question 2.
Use the Distributive Property to find 8 × 49.
Answer:
The equation is (8 × 40) + (8 × 9) and the property used is Distributive property.
Explanation:
Given that 8 × 49, by distributive property the equation will be
= 8 × (40 + 9)
= (8 × 40) + (8 × 9)
So, Distributive Property is a property that multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products.
Apply and Grow: Practice
Complete the equation. Identify the property shown.
Question 3.
1 × _____ = 17
Answer:
The equation is 1 × 17= 17 and the property used is Multiplication Properties of One.
Explanation:
The equation is 1 × 17 = 17.
The property used to complete this equation is Multiplication Properties of One which means the product of any number and 1 is that number. So the equation will be 1 × 17 = 17.
Question 4.
248 + 0 = ______
Answer:
The equation is 248 + 0= 248 and the property used is the Addition Property of Zero.
Explanation:
The equation is 248 + 0= 248.
The property used is the Addition Property of Zero which means the sum of any number and 0 is that number. So the equation will be 248 + 0= 248.
Question 5.
23 + 145 + 7 = 23 + 7 + _____
Answer:
The equation is 23 + 145 + 7= 23 + 7 + 145. And the property which is used is the Commutative property.
Explanation:
The equation is 23 + 145 + 7= 23 + 7 + 145. And the property which is used is the Commutative property.
Commutative Properties means changing the order of addends or factors does not change the sum or product. So the equation is 23 + 145 + 7= 23 + 7 + 145.
Question 6.
3 × (10 + 2) = (3 × 10) + (3 × ______)
Answer:
The equation is 3 × (10 + 2)= (3 × 10) + (3 × 2) and the property used is the Distributive Property.
Explanation:
The equation is 3 × (10 + 2)= (3 × 10) + (3 × 2)
The Distributive Property is a property in which Multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. So the equation is 3 × (10 + 2)= (3 × 10) + (3 × 2).
Use the Distributive Property to find the product.
Question 7.
5 × 97
Answer:
The equation is
5 × 97 = 5 × (90 + 7)
= (5 × 90) + (5 × 7) and the property used is Distributive property.
Explanation:
Given that 5 × 97, by distributive property the equation will be
= 5 × (90 + 7)
= (5 × 90) + (5 × 7)
So, Distributive Property is a property that multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. So the equation is
5 × 97 = 5 × (90 + 7)
= (5 × 90) + (5 × 7).
Question 8.
83 × 7
Answer:
The equation is
83 × 7 = 7 × (80 + 3)
= (7 × 80) + (7 × 3) and the property used is Distributive property.
Explanation:
Given that 7 × 83, by distributive property the equation will be
= 7 × (80 + 3)
= (7× 80) + (7 × 3)
So, Distributive Property is a property that multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. So the equation is
7 × 83 = 7 × (80 + 3)
= (7 × 80) + (7 × 3)
Use a property to find the sum or product. Identify the property you used.
Question 9.
4 + (6 + 27)
Answer:
The sum of 4 + (6 + 27) is 37 and the property which is used is the Commutative property.
Explanation:
The sum of 4 + (6 + 27) is 37 and the property which is used is the Commutative property.
Commutative Properties means changing the order of addends or factors does not change the sum or product. So the sum is 37.
Question 10.
5 × 49 × 0
Answer:
The product of 5 × 49 × 0 is 0 and the property used is Multiplication Properties of Zero.
Explanation:
The product of 5 × 49 × 0 is 0 and the property used is Multiplication Properties of Zero.
Multiplication Properties of Zero is the product of any number and 0 is 0. So 5 × 49 × 0 is 0.
Question 11.
11 + 16 + 89
Answer:
The sum of 11 + 16 + 89 is 116 and the property which is used is the Commutative property.
Explanation:
The sum of 11 + 16 + 89 is 116 and the property which is used is the Commutative property.
Commutative Properties means changing the order of addends or factors does not change the sum or product. So the sum is 116.
Question 12.
YOU BE THE TEACHER
Your friend uses the Distributive Property to find 4 × 46. Is your friend correct? Explain.
4 × 46 = 4 × (50 – 4)
= (4 × 50) – (4 × 4)
= 200 – 16
= 184
Answer:
Yes, my friend is correct. He uses distributive property correctly.
Explanation:
Yes, my friend is correct. By distributive property, the equation will be
4 × 46 = 4 × (50 – 4)
= (4 × 50) – (4 × 4)
= 200 – 16
= 184.
So, Distributive Property is a property that multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. So the equation is
Question 13.
Can you use the Associative Property with subtraction? Explain. Use an example to justify your answer.
Answer:
No, we cannot use the Associative Property with subtraction.
Explanation:
No, we cannot use the Associative Property with subtraction. As Associative property means changing the grouping of addends or factors does not change the sum or product. So Associative property can only be used for addition or multiplication. And the subtraction doesn’t have the associative property because for example if we take 20 and10 and subtract the first two numbers 20 minus 10 then the result will be 10. So changing the way of associating the numbers in subtraction can change the result. So the subtraction doesn’t have the associative property.
Think and Grow: Modeling Real Life
Example
There are three types of animals at a shelter. How many animals are there in all?

Find the number of each type of animal at the shelter.
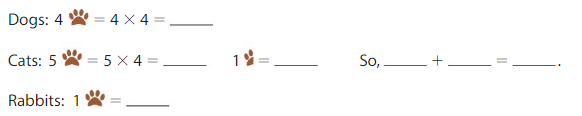
Add the numbers of dogs, cats, and rabbits.
16 + 22 + 4 = ____ + ____ + ____ Commutative Property of Addition
= _____ + _____ Add.
= _____ Add.
There are _____ animals in all.
Answer:
The total number of animals in the shelter is 42 animals.
Add the numbers of dogs, cats, and rabbits.
16 + 22 + 4 = 4 + 22 + 16 Commutative Property of Addition
= 26 + 16 Add.
= 42 Add.
There are 42 animals in all.
Explanation:
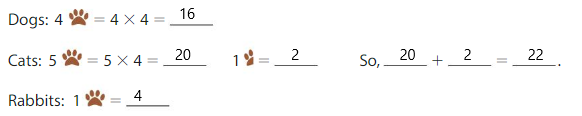
Given that each paw is equal to four pets. So the dog has four paws which means 4 × 4 = 16. The total number of dogs is 16 dogs. And cats have five paws and a half paw so the total number of cats is 5 × 4= 20 as one paw is equal to four so the half paw is two animals. So the total number of cats is 20 + 2= 22 cats. And rabbit has one paw so the total number of rabbits is 4 rabbits. So to find the total number of animals is we will add all the animals and add the numbers of dogs, cats, and rabbits. So
16 + 22 + 4 = 4 + 22 + 16 Commutative Property of Addition
= 26 + 16 Add.
= 42 Add.
There are 42 animals in all.
Show and Grow
Question 14.
You play three different video games in an evening. How many minutes do you play video games in all?

Answer:
The total number of minutes the video game is playing is 66 minutes.
Explanation:
Given that each clock is six minutes. And given that dancing has three clocks and a half clock. So the total number of minutes in playing dancing is 3 × 6= 18 minutes, as each clock is 6 minutes, so the half clock will be 3 minutes. So the total number of minutes in playing dancing is 18 + 3= 21 minutes. And given that puzzle has two clocks and a half clock, so the total number of minutes in playing puzzle is 1 × 6= 6 as each clock is 6 minutes, so the half clock will be 3 minutes. So the total number of minutes in playing dancing is 6 + 3= 9 minutes. And given that racing has six clocks. So the total number of minutes in playing racing is 6 × 6= 36 minutes. So the total number of minutes in playing dancing is 18 + 3= 21 minutes. So the total number of minutes the video game is playing is
21 minutes + 9 minutes + 36 minutes which is 66 minutes.
Question 15.
DIG DEEPER!
Tickets for a school play are sold out. The auditorium has 4 sections. Each section has 25 rows with 15 seats in each row. Each ticket costs $2. How much money is raised in ticket sales?
Answer:
The total amount raised in the ticket sale is $3,000.
Explanation:
As there are four sections in the auditorium and each section has 25 rows with 15 seats in each row and each ticket costs $2. So first we need to find the total number of seats. For that, we should multiple numbers of rows and the seats which are 25 × 15= 375 seats. And there are four sections, so 4 × 375= 1,500. So there are 1500 total seats. And each ticket costs $2, for 1500 seats it will be 1500 × 2= 3,000. So the total amount raised in the ticket sale is $3,000.
Number Properties Homework & Practice 2.1
Complete the equation. Identify the property shown.
Question 1.
687 × ____ = 0
Answer:
The equation is 687 × 0 = 0 and the property used is Multiplication Properties of Zero.
Explanation:
The equation is 687 × 0 = 0 and the property used is Multiplication Properties of Zero.
As Multiplication Properties of Zero is the product of any number and 0 is 0. So 687 × 0 is 0.
Question 2.
15 + 13 = 13 + _____
Answer:
The equation is 15 + 13 = 13 + 15 and the property which is used is the Commutative property.
Explanation:
The equation is 15 + 13 = 13 + 15 and the property which is used is the Commutative property.
As the Commutative Properties means changing the order of addends or factors does not change the sum or product. So the equation will be 15 + 13 = 13 + 15.
Question 3.
4 × 7 × 25 = 4 × _____ × 7
Answer:
The equation is 4 × 7 × 25 = 4 × 25 × 7 and the property used is Associative Property.
Explanation:
The equation is 4 × 7 × 25 = 4 × 25 × 7 and the property used is Associative Property.
As Associative Property means changing the grouping of addends or factors does not change the sum or product.
4 × 7 × 25 = 4 × 25 × 7
Question 4.
6 × (20 – 3) = (6 × 20) – (6 × _____)
Answer:
The equation is 6 × (20 – 3) = (6 × 20) – (6 × 3) and the property used is Distributive property.
Explanation:
The equation is 6 × (20 – 3) = (6 × 20) – (6 × 3) and the property used is Distributive property.
Distributive Property is a property of Multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products.
Use the Distributive Property to find the product.
Question 5.
4 × 78
Answer:
The product is
4 × 78 = 4 × (70 + 8)
= (4 × 70) + (4 × 8)
= 280 + 32
= 312
and the property used is the Distributive Property.
Explanation:
The product is
4 × 78 = 4 × (70 + 8)
= (4 × 70) + (4 × 8)
= 280 + 32
= 312
The Distributive Property is a property in which Multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. So the product of 4 × 78 is
= 4 × (70 + 8)
= (4 × 70) + (4 × 8)
= 280 + 32
= 312.
Question 6.
23 × 8
Answer:
The product is
23 × 8 = 8 × (20 + 3)
= (8 × 20) + (8 × 3)
= 160 + 24
= 184
and the property used is the Distributive Property.
Explanation:
The product is
23 × 8 = 8 × (20 + 3)
= (8 × 20) + (8 × 3)
= 160 + 24
= 184
The Distributive Property is a property in which Multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. So the product of 23 × 8 is
= 8 × (20 + 3)
= (8 × 20) + (8 × 3)
= 160 + 24
= 184.
Use a property to find the sum or product. Identify the property you used.
Question 7.
6 × 43
Answer:
The product is
6 × 43 = 6 × (40 + 3)
= (6 × 40) + (6 × 3)
= 240 + 18
= 258.
and the property used is the Distributive Property.
Explanation:
The product is
6 × 43 = 6 × (40 + 3)
= (6 × 40) + (6 × 3)
= 240 + 18
= 258.
The Distributive Property is a property in which Multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. So the product of 6 × 43 is
= 6 × (40 + 3)
= (6 × 40) + (6 × 3)
= 240 + 18
= 258.
Question 8.
339 + 0 + 54
Answer:
The equation is 23 + 145 + 7= 23 + 7 + 145. And the property which is used is the Commutative property.
Explanation:
The sum is 339 + 0 + 54 = 393. And the property which is used is the Commutative property.
Commutative Properties means changing the order of addends or factors does not change the sum or product. So the equation is 339 + 0 + 54 = 54 + 339 + 0.
Question 9.
25 × 8 × 2
Answer:
The equation is 25 × 8 × 2 = 400. And the property which is used is the Commutative property.
Explanation:
The product is 25 × 8 × 2 = 400. And the property which is used is the Commutative property.
Commutative Properties means changing the order of addends or factors does not change the sum or product. So the equation is 25 × 8 × 2 = 25 × 8 × 2.
Question 10.
Number Sense
To find 29 + (11 + 16), your friend adds 29 and 11. Then he adds 16 to the sum. Which property did he use and why?
Answer:
The property which is used is the Commutative property. And the equation can be written as
29 + 11 + 16 = 29 + 11 + 16.
Explanation:
Given equation is 29 + (11 + 16) and my friend adds 29 and 11 after that he adds 16 to find the sum. And the property which is used is the Commutative property. And Commutative Properties means changing the order of addends or factors does not change the sum or product. So the equation can be written as
29 + 11 + 16 = 29 + 11 + 16.
Question 11.
Writing
Explain how using properties can help you mentally find answers to problems.
Answer:
Using the properties like Commutative property, Distributive property, Associative Properties, Addition Property of Zero, Multiplication Properties of Zero & One helps us mentally in finding answers to problems by this process and we can solve the problems easily by these properties and everyone can identify this property. With these properties, we can write the equivalent expressions which help us to solve mental problems.
Question 12.
Number Sense
Newton uses two properties to rewrite the expression (4 × 23) × 25. Identify the properties he uses. Why would Newton use these properties?
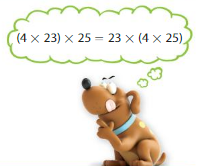
Answer:
The property Newton used is the Commutative property.
Explanation:
The property Newton used is the Commutative property. Newton uses Commutative Property because by Commutative property changing the order of addends or factors does not change the sum or product. So the equation can be written as 4 × 23 × 25. = 25 × 4 × 23.
Question 13.
Modeling Real Life
Before performing an experiment, students are asked to predict which substance will melt an ice cube the fastest. How many students make a prediction? Identify the property you used.

Answer:
The total number of students who have participated in the prediction is 76 students and the property used is commutative property.
Explanation:
Given that each emoji is 8 students, so the salt has two emojis that mean 2 × 8= 16 students. So the students who have predicted the salt are 16 students. And the sugar has three emojis and a half emoji that means 3 × 8= 24 students and a half emoji means, as each emoji is 8 students, so half emoji is 4 students and the total number of students is 24 + 4= 28 students. So the students who have predicted the sugar are 28 students. And the water has four emojis that means 4 × 8= 32 students. So the students who have predicted the water are 32 students.
The total number of students who have participated in the prediction is
16 students + 28 students + 32 students = 76 students. So the total number of students who have participated in the prediction is 76 students. And the property used is commutative property. And Commutative Properties means changing the order of addends or factors does not change the sum or product. So the equation can be written as
16 + 28 + 32= 32 + 16 +28.
Question 14.
Modeling Real Life
An apartment building has 35 floors with 12 apartments on each floor. There are 300 apartments that have 2 bedrooms. The rest of the apartments have 1 bedroom. How many 1-bedroom apartments are in the building? How can you use the Distributive Property to help solve this problem mentally?
Answer:
Review & Refresh
Find the sum. Check whether your answer is reasonable.
Question 15.
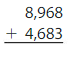
Answer:
By adding 8,968 and 4,683 we will get the sum of 13,651.
Explanation:
By adding 8,968 and 4,683 we will get the sum of 13,651. To check whether the answer is reasonable we will subtract 4,683 with 13,651 the difference will be 8,968. So the answer is reasonable.
Question 16.
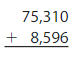
Answer:
By adding 75,310 and 8,596 we will get the sum of 83,906.
Explanation:
By adding 75,310 and 8,596 we will get the sum of 83,906. To check whether the answer is reasonable we will subtract8,596 with 83,906 the difference will be 75,310. So the answer is reasonable.
Question 17.
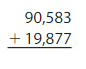
Answer:
By adding 90,583 and 19,877 we will get the sum of 110,460.
Explanation:
By adding 90,583 and 19,877 we will get the sum of 110,460. To check whether the answer is reasonable we will subtract 19,877 with 110,460 the difference will be 90,583. So the answer is reasonable.
Lesson 2.2 Order of Operations
Explore and Grow
Two students were asked to find the value of the expression below and they got different answers. Only one student has the correct answer. The students did not make any mistakes in their calculations. How did they get different answers?
24 + 16 ÷ 4 – 2
Answer:
The other student did not use the BODMAS rule so the other student calculation is not correct.
Explanation:
To find the value of the expression 24 + 16 ÷ 4 – 2 first we will divide 16 by 4 then the result will be 4. Now we will add result 4 with the number 24 which is 24 + 4= 28. And now we will subtract the number 2 with 28 which is
28 – 2= 26. This expression was done by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. And this was done by one student. Now the other student has done the same expression in a different way. The expression is 24 + 16 ÷ 4 – 2, so the other student solves the expression by first adding 24 and 16 which is 24 + 16= 40, and then we will divide 40 by 4, so the result will be 10. And now we will subtract 2 with 10 and the result will be 10 – 2= 8. So the other student’s answer will be 8 which is not correct because the other student did not use the BODMAS rule so the other student’s calculation is not correct.
Structure
Why is it important to have rules when finding values of expressions that contain more than one operation?
Answer:
It is important to have the rules when finding the values of expressions that contain more than one operation because the rules tell that the right order in which we will solve different parts of a math problem. And the order of operations is very important because it guarantees that we can all read and solve the problem in the same way.
Think and Grow: Use Order of Operations
Key Idea
A numerical expression is an expression that contains numbers and operations. When you evaluate a numerical expression, you find the value of the expression.
When evaluating a numerical expression, use a set of rules called the order of operations. These rules tell you the order in which to perform the operations.

Order of Operations
1. Perform operations in parentheses
2. Multiply and divide from left to right
3. Add and subtract from left to right
Example
Evaluate 19 – 18 ÷ 6.
Using the order of operations, divide first. Then subtract.

So, 19 – 18 ÷ 6 = _______.
Example
Evaluate 30 ÷ (3 + 7) × 2.
Using the order of operations, perform the addition in the parentheses first. Then multiply and divide from left to right.

So, 30 ÷ (3 + 7) × 2 = ______.
Show and Grow
Evaluate the expression.
Question 1.
24 + 4 ÷ 2
Answer:
The value of the expression 24 + 4 ÷ 2 is 26.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So first we will solve the division part of the expression which is 4 ÷ 2 = 2 and the result will be 2. Now we solve the addition part, we will add the result with 24 which is 24 + 2 = 26. So the value of the expression is 26.
Question 2.
12 + (10 – 3) × 8
Answer:
The value of the expression 12 + (10 – 3) × 8 is 68.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So first we will solve the parentheses part which is (10 – 3)= 7 and the result will be 7. Now we will solve the multiplication part which is 7 × 8= 56 and the result will be 56. And now we will solve the addition part which is 12 + 56= 68. So the value of the expression is 68.
Apply and Grow: Practice
Evaluate the expression.
Question 3.
25 + (10 ÷ 5)
Answer:
The value of the expression is 27.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So first we will solve the parentheses part which is (10 ÷ 5)= 2 and the result will be 2. Now we will add the result with 25 which is 25 + 2= 27. So the value of the expression is 27.
Question 4.
10 + 10 + 7
Answer:
The sum of the expression 10 + 10 +7 is 27.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. As there are no other expressions rather than addition we will perform addition to the given expression 10 + 10 + 7 and the sum of the expression
10 + 10 +7 is 27.
Question 5.
48 ÷ (8 – 2)
Answer:
The value of the expression 48 ÷ (8 – 2) is 8.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition and Subtraction. So first we will solve the parentheses which is (8 – 2)= 6. Now we will perform division operation for 48 by 6 and the result will be 8. So the value of the expression 48 ÷ (8 – 2) is 8.
Question 6.
(45 + 25) ÷ 10
Answer:
The value of the expression (45 + 25) ÷ 10 is 7.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition and Subtraction. So first will solve the parentheses part which is (45 + 25)= 70 and now we will perform division 70 ÷ 10 and the result will be 7. So the value of the expression (45 + 25) ÷ 10 is 7.
Question 7.
63 – 54 ÷ 9
Answer:
The value of the expression 63 – 54 ÷ 9 is 57.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition and Subtraction. Now first we will solve the division part which is 54 ÷ 9= 6 and the result is 6. Now we will subtract the result with 63 which is 63 – 6= 57. So the value of the expression 63 – 54 ÷ 9 is 57.
Question 8.
\(\left(\frac{1}{2}+\frac{1}{2}\right) \times 5\)
Answer:
The value of the expression \(\left(\frac{1}{2}+\frac{1}{2}\right) \times 5\) is 5.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the parentheses part which is \(\left(\frac{1}{2}+\frac{1}{2}\right) so the value will be 1. And now we will perform the multiplication part which is 1 × 5= 5. So the value of the expression [latex]\left(\frac{1}{2}+\frac{1}{2}\right) \times 5\) is 5.
Question 9.
15 + (16 – 6) × 1
Answer:
The value of the expression 15 + (16 – 6) × 1 is 25.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will perform the parentheses part which is (16 – 6)= 10 and the result will be 6. Now we will perform the multiplication part which is 10 × 1= 10 and the result will be 10. And now we will perform the addition which is 15 + 10 then the result will be 25. So the value of the expression 15 + (16 – 6) × 1 is 25.
Question 10.
(18 + 23 + 22) ÷ 9
Answer:
The value of the expression (18 + 23 + 22) ÷ 9 is 7.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will perform the parentheses part which is (18 + 23 + 22)= 63 and the result will be 63. Now we will perform division which is
63 ÷ 9= 7. So the value of the expression (18 + 23 + 22) ÷ 9 is 7.
Question 11.
80 – 6 × 5 × 2
Answer:
The value of the expression 80 – 6 × 5 × 2 will be 20.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the multiplication part which is 6 × 5 × 2= 60 and the result will be 60. Now we will solve the subtraction part which is 80 – 60= 20. So the value of the expression 80 – 6 × 5 × 2 will be 20.
Insert parentheses to make the statement true.
Question 12.
6 + 2 × 7 = 56
Answer:
The expression after inserting parentheses is (6 +2) × 7.
Explanation:
Given the expression is 6 + 2 × 7. So we will insert the parentheses for 6 + 2, then the expression will be
(6 +2) × 7. So we will solve the expression using the BODMAS rule, now first we will perform the parentheses part which is (6 +2)= 8. And now we will perform the multiplication part which is 8 × 7= 56. So the statement is true by inserting the parentheses for 6 + 2.
Question 13.
18 – 6 ÷ 2 + 5 = 11
Answer:
The expression after inserting parentheses is (18 – 6) ÷ 2 + 5.
Explanation:
Given the expression is 18 – 6 ÷ 2 + 5. So we will insert the parentheses for 18 – 6, then the expression will be
(18 – 6) ÷ 2 + 5. So we will solve the expression using the BODMAS rule, now first we will perform the parentheses part which is (18 – 6)= 12. And now we will perform division which is 12 ÷ 2= 6. Now we will perform the addition part which is 6 + 5= 11. So the statement is true by inserting the parentheses for 18 – 6.
Question 14.
10 + 2 × 4 – 1 = 16
Answer:
The statement is true by inserting parentheses for 4 – 1 and the expression is 10 + 2 ×(4 – 1).
Explanation:
Given the expression is 10 + 2 × 4 – 1. So we will insert the parentheses for 4 – 1, then the expression will be
10 + 2 ×(4 – 1). So we will solve the expression using the BODMAS rule, now first we will perform the parentheses part which is (4 – 1)= 3. And now we will perform the multiplication part which is 2 × 3= 6. And now we will add the result 6 with 10 which is 10 + 6= 16. So the statement is true by inserting parentheses for 4 – 1.
Question 15.
YOU BE THE TEACHER
Is Newton correct? Explain.
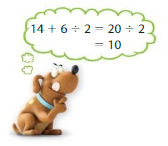
Answer:
No, Newton is not correct.
Explanation:
No, Newton is not correct. Because Newton did not use the BODMAS rule to solve the expression. By using the BODMAS rule first Newton should solve the division part and then he should solve the addition part.
Question 16.
Writing
Describe how you can evaluate 9 × (40 + 5) two different ways.
Answer:
The expression 9 × (40 + 5) can be solved by the BODMAS way and the other way to solve the expression is by Distributive property.
Explanation:
Given the expression is 9 × (40 + 5), so to solve the expression we will use the BODMAS rule. So by the BODMAS rule first we will solve the parentheses part which is (40 + 5)= 45 and then we will solve the multiplication part which s 9 × 45= 405. This process is one way to solve the given expression. Another way to solve the expression is by Distributive property and the equation can be solved as
9 × (40 + 5) = (9 × 40) + (9 + 5)
= 360 + 451
= 405.
and this property is called as Distributive property which means Distributive Property is a property of Multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products.
Think and Grow: Modeling Real Life
Example
A robotics team orders 14 shirts. The order has a $9 shipping fee. Use the expression 14 × 12 + 9 to find how much the team spends on the order.

Evaluate 14 × 12 + 9 using the order of operations.
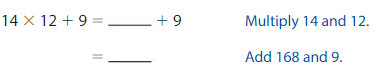
The team spends _____ on the order.
Answer:
The team spends $177 on the order.
Explanation:
As robotic team orders, 14 shirts and the order has a $9 shipping fee and the given expression is 14 × 12 + 9. We can solve this expression by the BODMAS rule in which BODMAS stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the multiplication part which is stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the multiplication part which is 14 × 12= 168 and then we will solve the addition part which is 168 + 9= 177. So the team spends $177 on the order.
Show and Grow
Question 17.
A parking garage has 7 floors with 109 spaces on each floor. There are 486 spaces being used. Use the expression 7 × 109 – 486 to find how many spaces are not being used.
Answer:
The number of spaces that are not being used is 1,367.
Explanation:
As a parking garage has 7 floors with 109 spaces on each floor and there are 486 spaces being used, so given expression is 7 × 109 – 486. So the given expression first we will solve the multiplication part by the BODMAS rule in which BODMAS stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So now first we will solve the multiplication part which is 7 × 109= 1,853 and then we will solve the subtraction part which is
1853 – 486= 1,367. So the number of spaces that are not being used is 1,367.
Question 18.
At a fair, you ride the swinging ship 3 times and the bumper cars 5 times. Use the expression (3 × 2) + (5 × 4) to find how many tickets you use in all.

Answer:
The number of tickets I have used is 26 tickets.
Explanation:
As a fair has a swinging ship and a bumper car and I rode the swinging ship 3 times and the bumper cars 5 times, so the given expression is (3 × 2) + (5 × 4). By the BODMAS rule first, we will solve the parentheses part and in which BODMAS stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So now first we will solve the parentheses part which is (3 × 2) + (5 × 4)= 6 + 20 and then we will solve the addition part which is 6 + 20= 26. So the number of tickets I have used is 26 tickets.
Question 19.
You download 128 songs and divide them into4 equal-sized playlists. You delete 1 playlist. Then you download 56 more songs. Use the expression 128 – (128 ÷ 4) + 56 to find how many songs you have now.
Answer:
The number of songs we had is 40 songs.
Explanation:
As I have downloaded 128 songs and divide them into 4 equal-sized playlists and then deleted 1 playlist. Then I have downloaded 56 more songs, so the given expression is 128 – (128 ÷ 4) + 56. By the BODMAS rule first we will solve the parentheses part and in which BODMAS stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So now first we will solve the parentheses part which is (128 ÷ 4)= 32 and now we will solve the addition part which is 32 + 56= 88, and now we will solve the subtraction part which is 128 – 88= 40. So the number of songs we have is 40 songs.
Question 20.
DIG DEEPER!
A politician buys 3 boxes of campaign buttons. There are 60 buttons in each box. He divides the buttons into4 equal groups. How many buttons are in each group?
Answer:
There will be 45 buttons in each group.
Explanation:
As a politician buys 3 boxes of campaign buttons and there are 60 buttons in each box. So the total number of buttons is 3 × 60= 180 buttons and then he divides the buttons into four equal groups. So the number of buttons in each group is 180 ÷ 4= 45. So there will be 45 buttons in each group.
Order of Operations Homework & Practice 2.2
Evaluate the expression.
Question 1.
(8 – 2) × 4
Answer:
The value of the expression (8 – 2) × 4 will be 24.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the parentheses part which is (8 – 2)= 6 and the result will be 6. Now we will solve the multiplication part which is 6 × 4= 24. So the value of the expression (8 – 2) × 4 will be 24.
Question 2.
7 + (6 ÷ 3)
Answer:
The value of the expression 7 + (6 ÷ 3) will be 10.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the parentheses part which is (6 ÷ 3)= 3 and the result will be 3. Now we will solve the addition part which is 7 + 3= 10. So the value of the expression 7 + (6 ÷ 3) will be 10.
Question 3.
5 × (6 + 2)
Answer:
The value of the expression 5 × (6 + 2) will be 40.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the parentheses part which is (6 + 2)= 8 and the result will be 8. Now we will solve the multiplication part which is 5 × 8= 40. So the value of the expression 5 × (6 + 2) will be 40.
Question 4.
21 + 42 ÷ 7
Answer:
The value of the expression 21 + 42 ÷ 7 will be 27.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the Division part which is 42 ÷ 7= 6 and the result will be 6. Now we will solve the addition part which is 21 + 6= 27. So the value of the expression 21 + 42 ÷ 7 will be 27.
Question 5.
\(\left(\frac{1}{4}+\frac{2}{4}+\frac{3}{4}\right)\) × 2
Answer:
The value of the expression \(\left(\frac{1}{4}+\frac{2}{4}+\frac{3}{4}\right)\) × 2 will be 3.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve parentheses part which is \(\left(\frac{1}{4}+\frac{2}{4}+\frac{3}{4}\right)\)= 6/4 and the result will be 3/2. Now we will solve the multiplication part which is 3/2 × 2= 3. So the value of the expression
\(\left(\frac{1}{4}+\frac{2}{4}+\frac{3}{4}\right)\) × 2 will be 3.
Question 6.
86 – 9 × 6
Answer:
The value of the expression 86 – 9 × 6 will be 32.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the multiplication part which is 9 × 6= 54 and the result will be 54. Now we will solve the subtraction part which is 86 – 54= 32. So the value of the expression 86 – 9 × 6 will be 32.
Question 7.
56 – 22 ÷ 2
Answer:
The value of the expression 56 – 22 ÷ 2 will be 45.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the division part which is 22 ÷ 2= 11 and the result will be 11. Now we will solve the subtraction part which is 56 – 11= 45. So the value of the expression 56 – 22 ÷ 2 will be 45.
Question 8.
27 + 11 × 4
Answer:
The value of the expression 27 + 11 × 4 will be 71.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the multiplication part which is 11 × 4= 44 and the result will be 44. Now we will solve the addition part which is 27 + 44= 71. So the value of the expression 27 + 11 × 4 will be 71.
Question 9.
21 – (12 + 6) ÷ 9
Answer:
The value of the expression 21 – (12 + 6) ÷ 9 will be 19.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the parentheses part which is (12 + 6)= 18 and the result will be 18. Now we will solve the division part which is 18 ÷ 9= 2 and now we will solve the subtraction part which is 21 – 2= 19. So the value of the expression 21 – (12 + 6) ÷ 9 will be 19.
Evaluate the expression.
Question 10.
9 × (5 + 15) – 42
Answer:
The value of the expression 9 × (5 + 15) – 42 will be 138.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the parentheses part which is (5 + 15)= 20 and the result will be 20. Now we will solve the multiplication part which is 9 × 20= 180 and now we will solve the subtraction part which is 180 – 42= 138. So the value of the expression 9 × (5 + 15) – 42 will be 138.
Question 11.
14 + 56 ÷ 7 – 6
Answer:
The value of the expression 14 + 56 ÷ 7 – 6 will be 16.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the division part which is 56 ÷ 7= 8 and the result will be 8. Now we will solve the addition part which is 14 + 8= 22 and now we will solve the subtraction part which is 22- 6= 16. So the value of the expression 14 + 56 ÷ 7 – 6 will be 16.
Question 12.
(106 + 350 + 244) ÷ 10
Answer:
The value of the expression (106 + 350 + 244) ÷ 10 will be 70.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will solve the parentheses part which is (106 + 350 + 244) and the result will be 700. Now we will solve the division part which is 700 ÷ 10= 70. So the value of the expression (106 + 350 + 244) ÷ 10 will be 70.
Insert parentheses to make the statement true.
Question 13.
36 – 9 ÷ 9 = 3
Answer:
The statement is true by inserting parentheses for 36 – 9.
Explanation:
Given the expression is 36 – 9 ÷ 9 = 3. So we will insert the parentheses for 36 – 9, then the expression will be
(36 – 9) ÷ 9. So we will solve the expression using the BODMAS rule, now first we will perform the parentheses part which is (36 – 9)= 27. And now we will perform the division part which is 27 ÷ 9= 3. So the statement is true by inserting parentheses for 36 – 9.
Question 14.
12 + 8 ÷ 4 + 1 = 6
Answer:
The statement is true by inserting parentheses for 12 + 8.
Explanation:
Given the expression is 12 + 8 ÷ 4 + 1 = 6. So we will insert the parentheses for 12 + 8, then the expression will be
(12 + 8) ÷ 4 + 1. So we will solve the expression using the BODMAS rule, now first we will perform the parentheses part which is (12 + 8)= 20. And now we will perform the division part which is 20 ÷ 4= 5, now we will solve the addition part which is 5 + 1=6. So the statement is true by inserting parentheses for 12 + 8.
Question 15.
10 + 4 × 12 – 6 = 34
Answer:
The statement is true by inserting parentheses for 12 – 6.
Explanation:
Given the expression is 10 + 4 × 12 – 6 = 34. So we will insert the parentheses for 12 + 8, then the expression will be 10 + 4 × (12 – 6). So we will solve the expression using the BODMAS rule, now first we will perform the parentheses part which is (12 – 6)= 6. And now we will perform the multiplication part which is 4 × 6= 24, now we will solve the addition part which is 10 + 24=34. So the statement is true by inserting parentheses for 12 – 6.
Question 16.
YOU BE THE TEACHER
Your friend says that because of the order of operations, the expressions are equivalent. Is your friend correct? Explain.
10 – (5 × 2) + 7 10 – 5 × 2 + 7
Answer:
Yes, my friend is correct.
Explanation:
Yes, my friend is correct. The expressions are equivalent because of the order of operations. By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So if we solve the expression without parentheses we will get the same result. So my friend is correct.
Question 17.
Number Sense
Which expressions have a value of 9?
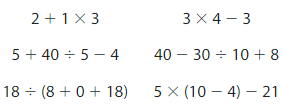
Answer:
On solving all the expressions the expression 5 + 40 ÷ 5 – 4, 5 × (10 – 4) – 21 has got the value of 9.
Explanation:
To check which expression has a value of 9, we will follow the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So the first expression is
2 + 1 × 3= 2 + 3, here first we will solve the multiplication part by the order of operations and then we will solve the addition part.
on solving we will get the result as 5.
So the first expression didn’t get the value as 9.
The second expression is
3 × 4 – 1= 12 – 1, here first we will solve the multiplication part by the order of operations and then we will solve the addition part.
on solving we will get the result as 11.
So the second expression didn’t get the value as 9.
The third expression is
5 + 40 ÷ 5 – 4 = 5 + 8 – 4
= 13 – 4, here first we will solve the division part by the order of operations then we will solve the addition part, and then the subtraction part.
On solving we will get the result as 9.
So the expression has the value 9.
The fourth expression is
40 – 30 ÷ 10 + 8 = 40 – 3 +8
= 40 – 11, here first we will solve the division part by the order of operations then we will solve the addition part, and then the subtraction part.
On solving we will get the result as 29.
So the expression didn’t get the value as 9.
The fifth expression is
18 ÷ (8+0+18) = 18 ÷ (26), here first we will solve the parentheses part by the order of operations then we will solve the division part. By seeing the solution we can say that the expression didn’t get the value 9.
The sixth expression is
5 × (10 – 4) – 21 = 5 × (6) – 21
= 30 – 21, here first we will solve the parentheses part by order of operations then we will solve the multiplication part, and then we will solve the subtraction part.
On solving we will get the result as 9.
So the expression has the value 9.
On solving all the expressions the expression 5 + 40 ÷ 5 – 4, 5 × (10 – 4) – 21 has got the value of 9.
Question 18.
Modeling Real Life
Fifth graders at a school write a paper about a historical person for a contest. There are 5 classes of 25 students and 1 class of 28 students participating in the contest. Use the expression 5 × 25 + 28 to find how many students participate in the contest.

Answer:
The number of students who participated in the contest is 153.
Explanation:
As there are 5 classes of 25 students and 1 class of 28 students participating in the contest and the given expression is 5 × 25 + 28. So, here first we will solve the multiplication part by the order of operations then we will solve the addition part. So
5 × 25 + 28= 125 + 28
On solving the expression we will get the result as 153. So the number of students who participated in the contest is 153.
Review & Refresh
Divide. Then check your answer.
Question 19.

Answer:
On dividing 832 ÷ 8 we will get the result as 104.
Explanation:
On dividing 832 ÷ 8 we will get the result as 104. To check the answer we will multiply the result 104 and 8 which is 104 × 8= 832.
Question 20.
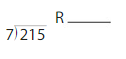
Answer:
On dividing 215 ÷ 7 we will get the result as 30.71.
Explanation:
On dividing 215 ÷ 7 we will get the result as 30.71. To check the answer we will multiply the result 30.71 and 7 which is 30.71 × 7= 214.97.
Question 21.
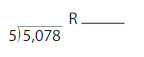
Answer:
On dividing 5,078 ÷ 5 we will get the result as 1015.6.
Explanation:
On dividing 5,078 ÷ 5 we will get the result as 1015.6. To check the answer we will multiply the result 1015.6 and 5 which is 1015.6 × 7= 5,078.
Lesson 2.3 Write Numerical Expressions
Explore and Grow
Write a real-life problem that can be represented by one of the expressions below. Switch papers with your partner. Which expression represents your partner’s problem? Explain.
7 × (8 + 5)
(7 × 8) + 5
Answer:
The expression represented by the partner is (7 × 8) + 5.
Explanation:
Given that the expressions are 7 × (8 + 5) and (7 × 8) + 5. So the solution for my problem is
7 × (8 + 5)= 7 × (12), here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. On solving we will get the result as 84. While checking my friend’s paper he solved the expression (7 × 8) + 5= 56 +5, here first we will solve the parentheses part by the order of operations then we will solve the addition part. On solving we will get the result as 61. AS the parentheses are different in the expression so the answer differs.
Make Sense of Problems
How can parentheses change the meaning of an expression? Explain.
Answer:
These parentheses in the expression represent that the expression or the equation should be solved first before any other calculation has done. The path between the parentheses represents as one number.
Think and Grow: Write an Interpret Expressions
Example
Write the words as an expression.

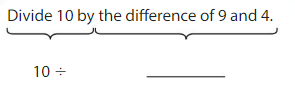
10 ÷ _______
The numerical expression is ______.
Answer:
The numerical expression is 10 ÷ (9 – 4).
Explanation:
The numerical expression using parenthesis is 10 ÷ (9 – 4). So, here first we will solve the parentheses part by the order of operations then we will solve the division part. So
10 ÷ (9 – 4) = 10 ÷ 5
on solving we will get the result as 5.
Example
Write the words as an expression. Then interpret the expression.
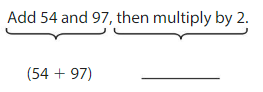
The numerical expression is _____.
The value of the expression is _______ times the sum 54 + 97.
Answer:
The numerical expression is (54 + 97) × 2.
The value of the expression is 2 times the sum of 54 + 97.
Explanation:
The numerical expression using parenthesis is (54 + 97) × 2. So, here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. So
(54 + 97) × 2 = 151 × 2
on solving we will get the result as 302.
The numerical expression is (54 + 97) × 2.
The value of the expression is 2 times the sum of 54 + 97.
Show and Grow
Write the words as an expression
Question 1.
Multiply 8 and 5, then divide by 4.
Answer:
The numerical expression using parenthesis is (8 × 5) ÷ 4.
Explanation:
The numerical expression using parenthesis is (8 × 5) ÷ 4. So, here first we will solve the parentheses part by the order of operations then we will solve the division part. So
(8 × 5) ÷ 4= 40 ÷ 4
on solving we will get the result as 10.
Question 2.
Multiply the sum of 14 and 18 by 4.
Answer:
The numerical expression using parenthesis is (14 + 18) × 4.
Explanation:
The numerical expression using parenthesis is (14 + 18) × 4. So, here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. So
(14 + 18) × 4= 32 × 4
on solving we will get the result as 128.
Write the words as an expression. Then interpret the expression.
Question 3.
Multiply 3 by the sum of 12 and 3.
Answer:
The numerical expression using parenthesis is 3 × (12 + 3).
Explanation:
The numerical expression using parenthesis is 3 × (12 + 3). So, here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. So
3 × (12 + 3)= 3 × 15
on solving we will get the result as 45.
Question 4.
Subtract 30 from 50, then divide by 10.
Answer:
The numerical expression using parenthesis is (50 – 30) ÷ 10.
Explanation:
The numerical expression using parenthesis is (50 – 30) ÷ 10. So, here first we will solve the parentheses part by the order of operations then we will solve the division part. So
(50 – 30) ÷ 10= 20 ÷ 10
on solving we will get the result as 2.
Apply and Grow: Practice
Write the words as an expression. Then interpret the expression.
Question 5.
Add 238 and 12, then multiply by 3.
Answer:
The numerical expression using parenthesis is (238 + 12) × 3.
Explanation:
The numerical expression using parenthesis is (238 + 12) × 3. So, here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. So
(238 + 12) × 3= 250 × 3
on solving we will get the result as 750.
Question 6.
Subtract 15 from 60, then divide by 9.
Answer:
The numerical expression using parenthesis is (60 – 15) ÷ 9.
Explanation:
The numerical expression using parenthesis is (60 – 15) ÷ 9. So, here first we will solve the parentheses part by the order of operations then we will solve the division part. So
(60 – 15) ÷ 9= 45 ÷ 9
on solving we will get the result as 5.
Write the words as an expression. Then evaluate the expression.
Question 7.
Multiply 5 by the difference of 25 and 20.
Answer:
The numerical expression is 5 × (25 – 20) and on evaluating we will get the value as 25.
Explanation:
The numerical expression using parenthesis is 5 × (25 – 20). So, here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. So
5 × (25 – 20)= 5 × 5
on solving we will get the result as 25.
Question 8.
Add the product of 60 and 4 to the product of 5 and 4.
Answer:
The numerical expression is (60 × 4) + (5 × 4) and on evaluating we will get the value as 260.
Explanation:
The numerical expression using parenthesis is (60 × 4) + (5 × 4). So, here first we will solve the parentheses part by the order of operations then we will solve the addition part. So
(60 × 4) + (5 × 4)= 240 + 20
on solving we will get the result as 260.
Write the expression in words.
Question 9.
13 + (4 × 6)
Answer:
Add 13 to the product of 4 and 6.
Explanation:
To expand the given expression 13 + (4 × 6) in words we will be written as
Add 13 to the product of 4 and 6.
Question 10.
(4 + 8) ÷ 2
Answer:
Add 4 and 8 and then divide by 2.
Explanation:
To expand the given expression 13 + (4 × 6) in words we will be written as
add 4 and 8 and then divide by 2.
Question 11.
Newton has $20. He spends $4 on lunch and $13 at the store. Write an expression to represent the situation.

Answer:
The expression can be represented as
$20 – ($13 + $4)= $20 – ($17)
Explanation:
As Newton has $20 and he spends $4 on lunch and $13 at the store. So the expression can be represented as
$20 – ($13 + $4)= $20 – ($17)
here first we will solve the parentheses part by the order of operations then we will solve the subtraction part. On solving we will get $3.
Question 12.
Writing
Explain how you know which operation to use when writing words as an expression.
Answer:
The operation to use when writing words as expressions are
The sum is used as addition and the difference is used as subtraction and the product is used as the product and the quotient is used as the division.
Question 13.
Number Sense
Write the words as an expression. Then use a property of addition to write an equivalent expression.
Add 9 to the sum of 21 and 6.
Answer:
The numerical expression of the given expression is 9 + (21 + 6) and the property used to solve the expression is Distributive property.
Explanation:
Given that the expression in words is Add 9 to the sum of 21 and 6. The numerical expression of the given expression is 9 + (21 + 6). The property we can use to solve the expression is distributive property. By Distributive Property is a property in which Multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. So by the distributive property, the expression will be solved as
9 + (21 + 6)= 9 + 27, here first we will solve the parentheses part by the order of operations then we will solve the addition part. On solving we will get the result as 36.
Think and Grow: Modeling Real Life
Example
On your turn of a word game, you draw the card shown and create the word MATH. Your word score is the sum of the points of the letters you use. How many points do you earn on your turn?

Write an expression.
Think: Add _____, _____, _____, and _____, then multiply by _____. (____ + ____ + _____ + _____) × _____
Interpret the expression.
You earn ____ times as many points as the value of your word score.
Answer:
Add 3 + 1 + 1 + 4, then multiply by 3. (3 + 1 + 1 + 4) × 3
You earn 3 times as many points as the value of your word score.
Explanation:
Given that the word M has a score of 3 and the word A has a score of 1 and the word T has a score of 1 and the word H has a score of 4. As word score is the sum of the points of the letters you use so we will add the total score which is 3 + 1 + 1 + 4= 9 and now we will multiply by 3 to triple the score. So the expression will be
(3 + 1 + 1 + 4) × 3= (9) × 3, here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. On solving we will get the result as 27.
Evaluate the expression.
(3 + 1 + 1 + 4) × 3 = ______ × _____
= ____
So, you earn _____ points on your turn.
Answer:
The points that I have earned in my turn is 27.
Explanation:
Given the expression is (3 + 1 + 1 + 4) × 3= (9) × 3, here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. On solving we will get the result as 27. So the points that I have earned in my turn are 27.
Show and Grow
Question 14.
You make 2 batches of fruit salad. How many cups of fruit do you use in all?

Answer:
The number of cups of fruit does we use in all is 14 cups.
Explanation:
As there are two cups of strawberries, 1 1/2 cups blueberries, 2 1/2 cups grapes,1 cup pineapple and there are two batches of fruit salad. So the expression will be 2 × ( 2 + 1 1/2 + 2 1/2 + 1).
2 × ( 2 + 1 1/2 + 2 1/2 + 1)= 2 × ((4 + 3 + 5 + 2)/2)
= 2 × (14/2) here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. On solving we will get the result as 14. So the number of cups of fruit do we use in all is 14 cups.
Question 15.
A customer places an online order for a video game that costs $49 and 3 books that each cost $12. Shipping costs $6. What is the total cost of the order?
Answer:
The numerical expression will be 49 + (3 × 12) + 6 on solving the result will be 91.
Explanation:
As the customer places an online order for a video game that costs $49 and 3 books and each book costs $12 and the shipping cost is $6. So the numerical expression will be 49 + (3 × 12) + 6.
49 + (3 × 12) + 6= 49 + 36 +6, here first we will solve the parentheses part by the order of operations then we will solve the addition part. On solving we will get the result as 91.
Question 16.
DIG DEEPER!
Eight students use2 sets of 52 cards to play a game. The cards are divided equally among the players. How many cards does each player get?
Answer:
The numerical expression is (2 × 52) ÷ 8 on solving the result will be 13.
Explanation:
As there are eight students and uses two sets of 52 cards to play a game, so the cards are equally divided among the players. So the numerical expression will be (2 × 52) ÷ 8.
(2 × 52) ÷ 8= 104 ÷ 8, here first we will solve the parentheses part by the order of operations then we will solve the division part. On solving we will get the result as 13.
Question 17.
DIG DEEPER!
How much more does it cost to rent 2 adult bikes for 4 hours than a tandem bike for 4 hours? Explain.

Answer:
It costs four times more than the tandem bike.
Explanation:
To rent a two adult bike for four hours then a tandem bike for four hours.
So the numerical expression will be (2 × 4) – 4.
(2 × 4) – 4= 8 – 4, here first we will solve the parentheses part by the order of operations then we will solve the subtraction part. On solving we will get the result as 4.
Write Numerical Expressions Homework & Practice 2.3
Write the words as an expression.
Question 1.
Add 10 to the quotient of 72 and 8.
Answer:
The numerical expression is (72 ÷ 8) + 10 and on evaluating we will get the value as 19.
Explanation:
The numerical expression using parenthesis is (72 ÷ 8) + 10. So, here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. So
(72 ÷ 8) + 10= 9 + 10
on solving we will get the result as 19.
Question 2.
Subtract 55 from the sum of 124 and 56.
Answer:
The numerical expression is (124 + 56) – 10 and on evaluating we will get the value as 170.
Explanation:
The numerical expression using parenthesis is (124 + 56) – 10. So, here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. So
(124 + 56) – 10= 180 – 10
on solving we will get the result as 170.
Write the words as an expression. Then interpret the expression.
Question 3.
Add 14 and 13, then divide by 3.
Answer:
The numerical expression is (14 + 13) ÷ 3 and on evaluating we will get the value as 9.
Explanation:
The numerical expression using parenthesis is (14 + 13) ÷ 3. So, here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. So
(14 + 13) ÷ 3= 27 ÷ 3
on solving we will get the result as 9.
Question 4.
Subtract 29 from 39, then multiply by \(\frac{1}{2}\).
Answer:
The numerical expression is (39 – 29) × 1/2 and on evaluating we will get the value as 5.
Explanation:
The numerical expression using parenthesis is (39 – 29) × 1/2. So, here first we will solve the parentheses part by the order of operations then we will solve the multiplication part. So
(39 – 29) × 1/2= 10 × 1/2
on solving we will get the result as 5.
Write the words as an expression. Then evaluate the expression.
Question 5.
Subtract the product of 5 and 8 from the product of 10 and 9.
Answer:
The numerical expression is (10 × 9) – (5 × 8) and on evaluating we will get the value as 50.
Explanation:
The numerical expression using parenthesis is (10 × 9) – (5 × 8). So, here first we will solve the parentheses part by the order of operations then we will solve the subtraction part. So
(10 × 9) – (5 × 8)= 90 – 40
on solving we will get the result as 50.
Question 6.
Add 15 to the quotient of 60 and 3.
Answer:
The numerical expression is 15 + (60 ÷ 3) and on evaluating we will get the value as 35.
Explanation:
The numerical expression using parenthesis is 15 + (60 ÷ 3). So, here first we will solve the parentheses part by the order of operations then we will solve the addition part. So
15 + (60 ÷ 3)= 15 + (20)
on solving we will get the result as 35.
Write the expression in words.
Question 7.
35 – (14 + 17)
Answer:
The expression in words is Subtract the sum of 14 and 17 with 35.
Explanation:
To expand the given expression 35 – (14 + 17) in words we will be written as
Subtract the sum of 14 and 17 with 35.
Question 8.
(30 – 20) × 10
Answer:
The expression in words is Subtract 30 and 20 and then multiply by 10.
Explanation:
To expand the given expression (30 – 20) × 10 in words we will be written as
Subtract 30 and 20 and then multiply by 10.
Question 9.
Descartes has $9. He works 5 hours and earns $8 each hour. Write an expression to represent the situation.
Answer:
The expression will be (5 × 8)+ 9 and on solving the expression we will get the result as 49.
Explanation:
As Descartes has $9 and he works 5 hours and earns $8 each hour, so the expression will be (5 × 8)+ 9.
(5 × 8)+ 9= 40 + 9, here first we will solve the parentheses part by the order of operations then we will solve the addition part. On solving the expression we will get the result as 49.
Question 10.
Open-Ended
Write a real-life problem that can be represented by the phrase “5 more than the sum of 15 and 7.”
Answer:
The numerical expression is (15 + 7) +5.
Explanation:
To represent the phrase 5 more than the sum of 15 and 7 in a numerical expression is (15 + 7) +5. As given that the 5 more than the sum of 15 and 7so we will add the number 5 to the sum of 15 and 7.
Question 11.
DIG DEEPER!
Write two different expressions that each represent the combined area of the rectangles. Then evaluate the expressions.
Answer:
Explanation:
Question 12.
Modeling Real Life
A music teacher replaces the strings on 3 violins, 2 violas, 4 cellos, and 1 bass. There are 4 strings on each of the instruments. How many strings does the teacher replace?
Answer:
The total number of strings replaced by the teacher is 37.
Explanation:
As music teacher replaces the strings on 3 violins, 2 violas, 4 cellos, and 1 bass and there are 4 strings on each of the instruments. So the teacher replaces 3 × 4= 12 violins and 2 × 4= 8 violas and 4 × 4= 16 cellos and 1 × 4= 1 bass. So the total number of strings replaced by the teacher is 12 + 8 + 16 + 1= 37.
Question 13.
DIG DEEPER!
A customer buys 2 shirts that cost $10 each and a pair of jeans that costs $14. What is the customer’s total after using the coupon?

Answer:
The customer’s total after using the coupon is $24.
Explanation:
As the customer buys 2 shirts that cost $10 each which is 2 × 10= 20 and a pair of jeans that costs $14 which is
2 × 14= 28. So the total purchase is 20 + 28= 48 and the coupon is 1/2 off on the entire purchase. This means
48 × 1/2= 24. So the customer’s total after using the coupon is $24.
Review & Refresh
Subtract.
Question 14.
9\(\frac{3}{4}\) – 5\(\frac{1}{4}\) = _____
Answer:
On subtracting 9\(\frac{3}{4}\) – 5\(\frac{1}{4}\) we will get the result as
4\(\frac{2}{4}\).
Explanation:
To subtract 9\(\frac{3}{4}\) – 5\(\frac{1}{4}\) first we need to convert mixed fraction into improper fraction. So the improper fraction will be \(\frac{39}{4}\) – \(\frac{21}{4}\). As the denominator is equal which is 4 so on subtracting \(\frac{39}{4}\) – \(\frac{21}{4}\) we will get the result as \(\frac{18}{4}\). So the mixed fraction of the result is 4\(\frac{2}{4}\).
Question 15.
6\(\frac{1}{3}\) – 3\(\frac{1}{3}\) = ______
Answer:
On subtracting 6\(\frac{1}{3}\) – 3\(\frac{1}{3}\) we will get the result as
\(\frac{3}\).
Explanation:
To subtract 6\(\frac{1}{3}\) – 3\(\frac{1}{3}\) first we need to convert mixed fraction into improper fraction. So the improper fraction will be \(\frac{19}{3}\) – \(\frac{10}{3}\). As the denominator is equal which is 3 so on subtracting \(\frac{19}{3}\) – \(\frac{10}{3}\) we will get the result as \(\frac{9}{3}\) which is \(\frac{3}\).
Question 16.
4\(\frac{7}{12}\) – 1\(\frac{11}{12}\) = ______
Answer:
On subtracting 4\(\frac{7}{12}\) – 1\(\frac{11}{12}\) we will get the result as
\(\frac{8}{3}\).
Explanation:
To subtract 4\(\frac{7}{12}\) – 1\(\frac{11}{12}\) first we need to convert mixed fraction into improper fraction. So the improper fraction will be \(\frac{55}{12}\) – \(\frac{23}{12}\). As the denominator is equal which is 12 so on subtracting \(\frac{55}{12}\) – \(\frac{23}{12}\) we will get the result as \(\frac{32}{12}\) which is \(\frac{8}{3}\).
Lesson 2.4 Evaluate Expressions with Grouping Symbols
Explore and Grow
Write the words as an expression. How is the expression different from the expressions you wrote in previous lessons?
Multiply the sum of 4 and 5 by the difference of 8 and 7.
Answer:
The numerical expression is ( 4 + 5 ) × (8 – 7 ) and on evaluating we will get the result as 9.
Explanation:
Given, Multiply the sum of 4 and 5 by the difference of 8 and 7.
the sum of 4 and 5 is ( 4 + 5 )
the difference between 8 and 7 is ( 8 – 7 )
And the Multiplication of these two is ( 4 + 5 ) × (8 – 7 ) = 9 × 1 = 9 .
Here we used simple mathematic rules for the expression other than using any properties and methods. And here we have only one pair of grouping symbols.
Precision
How can you evaluate an expression that has more than one pair of parentheses?
Answer: The expressions having more than one parenthesis can be evaluated by performing grouping symbols and in the next step, multiply and divide from left to right, Add and subtract from left to write if there are any,
parentheses( ), brackets [ ], braces { } are very helpful in grouping the symbols and to evaluate the numerical expression by performing inside operations parentheses, inside brackets, or inside braces.
Think and Grow: Evaluate with Grouping Symbols
Key Idea
Parentheses ( ), brackets [ ], and braces { } are called grouping symbols. You can write and evaluate numerical expressions that have more than one pair of grouping symbols.

Order of Operations (with Grouping Symbols)
1. Perform operations in grouping symbols.
2. Multiply and divide from left to right.
3. Add and subtract from left to right.
Example
Evaluate (25 – 5) ÷ (3 + 1).

So, (25 – 5) ÷ (3 + 1) = ______ .
Example
Evaluate [60 – (3 + 7)] × 5.

Show and Grow
Evaluate the expression.
Question 1.
(18 – 12) × (8 ÷ 4)
Answer:
On evaluating we will get the result as 12
Explanation:
Given that the numerical expression is (18 – 12) × (8 ÷ 4)
Firstly perform the operations within the parentheses,
Then we have,(8 ÷ 4) = 2,
(18 – 12) = 6, and now we will perform the multiplication part.
To evaluate the expression, multiply the resulting output from the inside parentheses operations, then 6 × 2 = 12
So , (18 – 12) × (8 ÷ 4) = 12
Question 2.
35 – [6 × (1 + 4)]
Answer:
On evaluating we will get the result as 5.
Explanation:
Given that the numerical expression is 35 – [6 × (1 + 4)]
Firstly perform the operations within the parentheses,
we have , (1 + 4) = 5 ,
Now performing operation inside brackets we get, [6 × 5] = 30,
and now we will perform the subtraction part
Next, apply the resulted output in the expression then we have, 35 – 30 = 5.
So, 35 – [6 × (1 + 4)] = 5.
Apply and Grow: Practice
Evaluate the expression.
Question 3.
(60 – 12) ÷ (3 + 5)
Answer:
On evaluating we will get the result as 6
Explanation:
Given that the numerical expression is (60 – 12) ÷ (3 + 5)
Firstly perform the operations within the parentheses,
we have , (60 – 12) = 48 ,
(3 + 5) = 8, now we will perform the subtraction part
Next, Divide the resulted outputs, we get 48 ÷ 8 = 6.
So , (60 – 12) ÷ (3 + 5) = 6
Question 4.
95 – (26 + 14) × (4 ÷ 2)
Answer:
On evaluating we will get the result as 15
Explanation:
Given that the numerical expression is 95 – (26 + 14) × (4 ÷ 2)
Firstly perform the operations within the parentheses,
we have (26 + 14) = 40 ,
(4 ÷ 2) = 2, now we will perform the multiplication part and then we will perform the subtraction part.
Now we have the given expression as 95 – ( 40 × 2 ), And calculating the inside parentheses we get ( 40 × 2 )= 80
Then 95 – 80 = 15
So , 95 – (26 + 14) × (4 ÷ 2) = 15 .
Question 5.
(8 + 2) × (13 + 7 + 5)
Answer:
On evaluating we will get the result as 250
Explanation:
Given that the numerical expression is (8 + 2) × (13 + 7 + 5)
Firstly perform the operations within the parentheses,
we have (8 + 2) = 10,
(13 + 7 + 5) = 20, and now we will perform the multiplication part.
To evaluate the given expression apply the resulted output as 10 × 25= 250
So, (8 + 2) × (13 + 7 + 5) = 250.
Question 6.
2 × [(96 – 72) ÷ 8]
Answer:
On evaluating the numerical expression the result is 72.
Explanation:
Given that the numerical expression is 2 × [(96 – 72) ÷ 8]
Firstly perform the operations within the parentheses,
we have (96 – 72) = 24,
[24 ÷ 8]= 3, and now we will perform the multiplication part.
To evaluate the given expression apply the resulted output as 24 × 3= 72
So, 2 × [(96 – 72) ÷ 8]= 72.
Question 7.
[(4 – 9) – (30 ÷ 6)] × 4
Answer:
On evaluating the expression we will get the result as 40.
Explanation:
Given that the numerical expression is [(4 – 9) – (30 ÷ 6)] × 4
Firstly perform the operations within the parentheses,
we have (4 – 9) = (-5),
(30 ÷ 6) =5 which is [-5 -5]= 10 and now we will perform the multiplication part.
To evaluate the given expression apply the resulted output as 10 × 4= 40
So, [(4 – 9) – (30 ÷ 6)] × 4 = 40.
Question 8.
36 + {[(7 + 5) ÷ 6 × 9] + 24}
Answer:
Write the words as an expression. Then evaluate the expression.
Question 9.
Divide the sum of 35 and 28 by the sum of 3 and 4.
Answer:
The numerical expression is (35 + 28) ÷ (3 + 4) and on evaluating we will get the value as 9.
Explanation:
The numerical expression using parenthesis is (35 + 28) ÷ (3 + 4). So, here first we will solve the parentheses part by the order of operations then we will solve the division part. So
(35 + 28) ÷ (3 + 4)= 63 ÷ 7
on solving we will get the result as 9.
Question 10.
Add 11 to the product of 4 and 6, then divide by 5.
Answer:
The numerical expression is [(4 × 6) + 11] ÷ 5 and on evaluating we will get the value as 9.
Explanation:
The numerical expression using parenthesis is [(4 × 6) + 11] ÷ 5. So, here first we will solve the parentheses part by the order of operations then we will solve the addition part after that we will solve the division part. So
(35 + 28) ÷ (3 + 4)= 63 ÷ 7
on solving we will get the result as 9.
Question 11.
Reasoning
Will the value of {3 + [(38 – 10) – 1]} ÷ 3 change when the braces are removed? Explain.
Answer: Yes, the value will be changed if we remove the braces.
Explanation:
Yes, the value will be changed if we remove the braces because if the expression with braces means first we will solve the part of the braces and then we will solve by the order of operations. So by that, the value of the expression will be changed when the braces are removed.
Question 12.
DIG DEEPER!
Use each symbol once to make the number sentence true.

Answer:
The numerical expression will be (8 + 2) × (20 ÷ 4) – 11.
Explanation:
The numerical expression will be (8 + 2) × (20 ÷ 4) – 11. Let’s solve the expression to check the answer.
(8 + 2) × (20 ÷ 4) – 11= (10) × (5) – 11
= 50 – 11, here first we will solve the parentheses part by the order of operations then we will solve the addition part after that we will solve the subtraction part. On solving we will get the result as 39.
Think and Grow: Modeling Real Life
Example
A woman walks 2 miles from her house to the lake, walks 3 laps on the sidewalk around the lake, then walks2 miles back to her house. She does this each day for 3 days. How many miles does the woman walk in all?

Think: How many laps does she walk around the lake? How far does she walk to and from her house?
Write an expression.
[____ + (_____ × _____) + _____] × _____
Evaluate the expression.
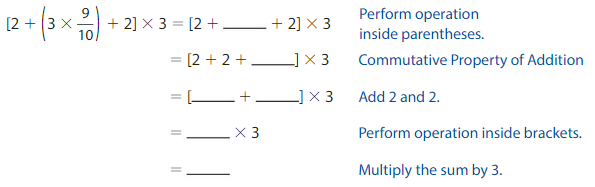
So, the woman walks ______ miles in all.
Show and Grow
Question 13.
You collect 12 coins and 4 gems, complete 2 missions, and fail to complete 1 mission. How many points do you earn?
Answer:
The total number of points earned is 175.
Explanation:
The number of coins collected is 12, so the number of points earned for one coin is 5 so for 12 coins it will be
12 × 5= 60 points and the number of gems collected is 4, so the number of points earned for each gem is 10 so for 4 gems it will be 4 × 10= 40 points. The completed missions is 2, so the number of points earned for completing one mission is 50 so for 2 missions it will be 2 × 50= 100 points and the missions failed is 1, so the number of points lost for failing one mission is -25 so for 1 failed mission it will be 1× -25= -25 points. So the total number of points earned is (60 + 40 + 100) – 25= 200 -25, here first we will solve the parentheses part by the order of operations then we will solve the addition part after that we will solve the subtraction part. On solving we will get the result as 175. So the total number of points earned is 175.
Question 14.
DIG DEEPER!
A book has 200 pages. You read 10 pages twice each day for 1 week. What fraction of the book, in tenths, do you have left to read?
Answer:
Th fraction in tenths is 3/10.
Explanation:
As the book has 200 pages and 10 pages were read twice a day for a week as a week means seven days and twice a day means 2 × 7= 14. So the number of pages were read is 14 × 10= 140 pages. And the number of pages left is 200 – 140= 60. So to represent this in a fraction it will be 60/200 which is 3/10.
Evaluate Expressions with Grouping Symbols Homework & Practice 2.4
Evaluate the expression.
Question 1.
15 ÷ (5 × 1) – (2 × 1)
Answer:
On evaluating the given expression result will be 5.
Explanation:
Given the numerical expression is 15 ÷ (5 × 1) – (2 × 1). By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will perform the parentheses part which is (5 × 1) – (2 × 1)= 5 – 2= 3 and the result will be 3. Now we will perform division which is
15 ÷ 3= 5. So the value of the expression 15 ÷ (5 × 1) – (2 × 1) is 5.
Question 2.
(7 + 9) ÷ (2 + 4 + 2)
Answer:
On evaluating the given expression we will get the result as 2.
Explanation:
Given the numerical expression is (7 + 9) ÷ (2 + 4 + 2). By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will perform the parentheses part which is (7 + 9) ÷ (2 + 4 + 2)= 16 ÷ 8 and the result will be 16 ÷ 8. Now we will perform division which is
16 ÷ 8= 2. So the value of the expression (7 + 9) ÷ (2 + 4 + 2) is 2.
Question 3.
(1 + 5) × (2 + 3)
Answer:
On evaluating the given expression result will be 25.
Explanation:
Given the numerical expression is (1 + 5) × (2 + 3). By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will perform the parentheses part which is (1 + 5) × (2 + 3)= 5 × 5 and the result will be 5 × 5. Now we will perform the multiplication part which is 5 × 5= 25. So the value of the expression
(1 + 5) × (2 + 3) is 25.
Question 4.
[(16 – 14) + (9 × 4)] ÷ 2
Answer:
On evaluating the given expression result will be 9.
Explanation:
Given the numerical expression is [(16 – 14) + (9 × 4)] ÷ 2. By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will perform the parentheses part which is (16 – 14) + (9 × 4)= 2 + 36 and the result will be 38. Now we will perform the division part which is 38 ÷ 2= 19. So the value of the expression
[(16 – 14) + (9 × 4)] ÷ 2 is 19.
Question 5.
70 ÷ [(463 – 443) ÷ 2]
Answer:
On evaluating the given expression result will be 7.
Explanation:
Given the numerical expression is 70 ÷ [(463 – 443) ÷ 2]. By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will perform the parentheses part which is (463 – 443)= 20 and the result will be 20. Now we will perform the division part which is 20 ÷ 2= 10. And there is another division part which is 70 ÷ 10= 70. So the value of the expression 70 ÷ [(463 – 443) ÷ 2] is 7.
Question 6.
9 × {[14 ÷ 2 + (4 – 1)] – 8}
Answer:
On evaluating the given expression result will be 18.
Explanation:
Given the numerical expression is 9 × {[14 ÷ 2 + (4 – 1)] – 8}. By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. Now first we will perform the parentheses part which is (4 – 1)= 3 and the result will be 3. Now we will perform the other parentheses part which is [14 ÷ 2 + (3)] = 7 + 3 and the result will be 10. Now we will perform the other parentheses part which is {10 – 8}= 2. Now we will perform the multiplication part which is 9 × 2= 18. So the value of the expression 9 × {[14 ÷ 2 + (4 – 1)] – 8} is 18.
Write the words as an expression. Then evaluate the expression.
Question 7.
Multiply the sum of 4 and 5 by the difference of 14 and 8.
Answer:
The numerical expression is (4 + 5) × (14 – 8) on evaluating the numerical expression we will get the result as 54.
Explanation:
Given that Multiply the sum of 4 and 5 by the difference of 14 and 8, so to represent this in an expression it will be (4 + 5) × (14 – 8). Now we will solve the numerical expression which is (4 + 5) × (14 – 8) = 9 × 6
Now first we have solved the parentheses part which is (4 + 5) × (14 – 8) and the result will be 9 × 6. And then we will perform the multiplication part which is 9 × 6= 54. So on evaluating the numerical expression we will get the result as 54.
Question 8.
Add 23, 26, and 17, then divide by 7.
Answer:
The numerical expression is (23 +26 +17) ÷ 7 on evaluating the numerical expression we will get the result as 9.4.
Explanation:
Given that Add 23, 26, and 17, then divide by 7, so to represent this in an expression it will be (23 +26 +17) ÷ 7. Now we will solve the numerical expression which is (23 +26 +17) ÷ 7= 66 ÷ 7
Now first we have solved the parentheses part which is (23 +26 +17) and the result will be 66. And then we will perform the division part which is 66 ÷ 7= 9.4. So on evaluating the numerical expression we will get the result as 9.4.
Question 9.
Writing
Explain how to evaluate the expression.
8 × [(36 – 33) × 2]
Answer:
On evaluating the numerical expression we will get the result as 48.
Explanation:
Given that the numerical expression is 8 × [(36 – 33) × 2]= 8 × [3 × 2]
Now first we have solved the parentheses part which is (36 – 33) and the result will be 3 and then we will perform the other parentheses part which is [3 × 2]= 6. And then we will perform the multiplication part which is
8 × 6= 48. So on evaluating the numerical expression we will get the result as 48.
Question 10.
Open-Ended
Write and evaluate two equivalent numerical expressions that show the Distributive Property.
Answer:
The two numerical equations are 5 × (90 + 7) and 83 × 7.
Explanation:
Let the equation be 5 × 97, by distributive property the equation will be
= 5 × (90 + 7)
= (5 × 90) + (5 × 7)
So, Distributive Property is a property that multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. So the equation is
5 × 97 = 5 × (90 + 7)
= (5 × 90) + (5 × 7).
Let the equation is 83 × 7, by distributive property the equation will be
= 7 × (80 + 3)
= (7× 80) + (7 × 3)
So, Distributive Property is a property that multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. So the equation is
7 × 83 = 7 × (80 + 3)
= (7 × 80) + (7 × 3)
Question 11.
Modeling Real Life
Your friend has 3 California postcards, 2 Hawaii postcards, and 4 New York postcards. He gives 1 postcard away, then divides the rest equally among 4 pages of a scrapbook. How many postcards are on each page?
Answer:
Question 12.
Modeling Real Life
A nutritionist recommends that fifth graders should eat about 305 grams of fruit each day.You eat the apple shown. How many more grams of fruit should you eat today?
Answer:
Review & Refresh
Find the product. Check whether your answer is reasonable.
Question 13.
639 × 5 = _____
Answer:
The product of 639 × 5= 3195.
Explanation:
The product of 639 × 5 is 3,195. So to check the answer is reasonable we will divide the result by 5 which is
3195 ÷ 5= 639. So the answer is reasonable.
Question 14.
7 × 1,926 = _____
Answer:
The product of 7 × 1,926 is 13,482.
Explanation:
The product of 7 × 1,926 is 13,482. So to check the answer is reasonable we will divide the result by 7 which is
13,482 ÷ 7= 1,926. So the answer is reasonable.
Question 15.
507 × 3 = ______
Answer:
The product of 507 × 3 is 1,521.
Explanation:
The product of 507 × 3 is 1,521. So to check the answer is reasonable we will divide the result by 3 which is
1,521 ÷ 3= 507. So the answer is reasonable.
Numerical Expressions Performance Task
Atoms are the basic building blocks of matter. When two or more atoms bond together, they form a molecule or a compound.
• The chemical formula for a water molecule is H2O because it has 2 atoms of hydrogen (H) and 1 atom of oxygen (O).
• The chemical formula for the compound sodium chloride, also known as table salt, is NaCl because it has 1 atom of sodium (Na) and 1 atom of chlorine (Cl) in a repeating pattern.
Question 1.
How many atoms are in 52 molecules of water?
Answer:
Question 2.
You and your friend want to make models for a science fair.
a. Your friend wants to make a model of sodium chloride. The model has the same number of green and orange atoms. There are 4 × 4 × 4 atoms in all. How many orange atoms do you need?
b. You make a model of a salt-water mixture. You use 14 atoms of sodium, 14 atoms of chlorine, and 10 molecules of H2O. Write an expression that represents the number of atoms in your salt-water model. Use the Distributive Property to rewrite your expression. Find the number of atoms in your model.
c. You and your friend buy 3 boxes of foam balls to represent atoms. There are 45 foam balls in each box. How many foam balls are left after you and your friend make the models above?
Answer:
Numerical Expressions Activity
Expression Boss
Directions:
1. Each player rolls three dice to complete the numerical expression. Players can arrange the numbers however they choose.
2. Each player evaluates the numerical expression.
3. Players compare their values. The player with the greater value earns one point.
4. If the values are equal, each player earns one point.
5. The player with the most points at the end of the game wins!

Answer:
Numerical Expressions Chapter Practice
2.1 Number Properties
Complete the equation. Identify the property shown.
Question 1.
56 × _____ = 0
Answer:
The product of 56 × 0 is 0 and the property used is Multiplication Properties of Zero.
Explanation:
The product of 56 × 0 is 0 and the property used is Multiplication Properties of Zero.
As Multiplication Properties of Zero is the product of any number and 0 is 0. So 56 × 0 is 0.
Question 2.
8 + (242 + 32) = (8 + 242) + _____
Answer:
The sum of 8 + (242 + 32) = (8 + 242) + 32 and the property which is used is the Commutative property. And the sum of the given expression is 282.
Explanation:
Given the expression is 8 + (242 + 32) = (8 + 242) + 32 and the property which is used is the Commutative property. Commutative Properties means changing the order of addends or factors does not change the sum or product. And the sum of the given expression is 282.
Use the Distributive Property to find the product.
Question 3.
8 × 64
Answer:
The equation is 8 × 64= 8 × (60 + 4)
= (8 × 60) + (8 × 4) and the property used is Distributive property.
And the product of the given expression is 512.
Explanation:
Given that 8 × 64, by distributive property the equation will be
= 8 × (60 + 4)
= (8 × 60) + (8 × 4)
So, Distributive Property is a property that multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. And the product of the given expression is 512.
Question 4.
57 × 9
Answer:
The equation is 57 × 9= 9 × (50 + 7)
= (9 × 50) + (9 × 7) and the property used is Distributive property.
And the product of the given expression is 513.
Explanation:
Given that 57 × 9, by distributive property the equation will be
= 9 × (50 + 7)
= (9 × 50) + (9 × 7)
So, Distributive Property is a property that multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. And the product of the given expression is 513.
Use a property to find the sum or product. Identify the property you used.
Question 5.
3 × 92
Answer:
The equation is 3 × 92= 3 × (90 + 2)
= (3 × 90) + (3 × 2) and the property used is Distributive property.
And the product of the given expression is 276.
Explanation:
Given that 3 × 92, by distributive property the equation will be
= 3 × (90 + 2)
= (3 × 90) + (3 × 2)
So, Distributive Property is a property that multiplying a sum (or difference) by a number is the same as multiplying each number in the sum (or difference) by the number and adding (or subtracting) the products. And the product of the given expression is 276.
Question 6.
41 × 6 × 0
Answer:
The product of 41 × 6 × 0 is 0 and the property used is Multiplication Properties of Zero.
Explanation:
The product of 41 × 6 × 0 is 0 and the property used is Multiplication Properties of Zero.
As Multiplication Properties of Zero is the product of any number and 0 is 0. So 41 × 6 × 0 is 0.
Question 7.
13 + 24 + 57
Answer:
The sum of 13 + 24 + 57 = 24 + 57 + 13 and the property which is used is the Commutative property. And the sum of the given expression is 94.
Explanation:
Given the expression is 13 + 24 + 57 = 24 + 57 + 13 and the property which is used is the Commutative property. Commutative Properties means changing the order of addends or factors does not change the sum or product. And the sum of the given expression is 94.
Question 8.
Modeling Real Life
The graph shows the number Favorite Apple of votes each apple received. How many people were surveyed? Identify the property you used.

Answer:
The total number of people surveyed is 46. And the property which can be used is the Commutative property
Explanation:
As given that each apple image is equal to four votes, so to know how many people are surveyed let’s first find the count of the apples and then the count of the votes. So Fuji has four apple images and a half apple image, so the total number of votes for Fuji is 4×4= 16 and a half apple image means two votes. So the total number of votes is 16 + 2= 18 votes. So the total number of votes for Fuji is 18 votes. And Granny Smith has three apple images, so the total number of votes for Granny Smith is 3×4= 12. And Honeycrisp has four apple images, so the total number of votes for Granny Smith is 4×4= 16. So the total number of people surveyed is 18 + 12 + 16= 46.
And the property which can be used is the Commutative property, as the Commutative Properties means changing the order of addends or factors does not change the sum or product. So the expression can be written as 18 + 12 + 16= 16 + 18 +12.
2.2 Order of Operations
Evaluate the expression.
Question 9.
18 × (9 – 3) ÷ 2
Answer:
The value of the expression 18 × (9 – 3) ÷ 2 is 54.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So first we will solve the parentheses part which is (9 – 3)= 6 and the result will be 6. Now we will solve the division part which is 6 ÷ 2= 3 and the result will be 3. And now we will solve the multiplication part which is 18 × 3= 54. So the value of the expression is 54.
Question 10.
50 – 18 ÷ 3 × 7
Answer:
The value of the expression 50 – 18 ÷ 3 × 7 is 8.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So first we will solve the division part which is 18 ÷ 3= 6 and the result will be 6. Now we will solve the multiplication part which is 6 × 7= 42 and the result will be 42. And now we will solve the subtraction part which is 50 – 42= 8. So the value of the expression is 8.
Question 11.
(36 + 14) × 4 ÷ 5
Answer:
The value of the expression (36 + 14) × 4 ÷ 5 is 40.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So first we will solve the parentheses part which is (36 + 14)×4= 50 × 4 and the result will be 200. Now we will solve the division part which is
200 ÷ 5 = 40 and the result will be 40. So the value of the expression is 40.
Question 12.
Number Sense
Which expressions have a value of 6?
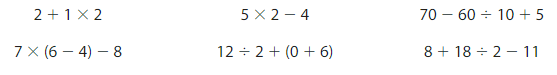
Answer:
2.3 Write Numerical Expressions
Write the words as an expression. Then interpret the expression.
Question 13.
Multiply 8 by the difference of 54 and 49.
Answer:
The numerical expression is (54 – 49) × 8 on evaluating the numerical expression we will get the result as 40.
Explanation:
Given that Multiply 8 by the difference of 54 and 49, so to represent this in an expression it will be (54 – 49) × 8. Now we will solve the numerical expression which is (54 – 49) × 8 = 5 × 8
Now first we have solved the parentheses part which is (54 – 49) and the result will be 5. And then we will perform the multiplication part which is 5 × 8= 40. So on evaluating the numerical expression we will get the result as 40.
Question 14.
Subtract 58 from 94, then divide by4.
Answer:
The numerical expression is (94 – 58) ÷ 4 on evaluating the numerical expression we will get the result as 9.
Explanation:
Given that Subtract 58 from 94, then divide by4, so to represent this in an expression it will be (94 – 58) ÷ 4. Now we will solve the numerical expression which is (94 – 58) ÷ 4= 36 ÷ 4
Now first we have solved the parentheses part which is (94 – 58) and the result will be 36. And then we will perform the division part which is 36 ÷ 4= 9. So on evaluating the numerical expression we will get the result as 9.
Question 15.
Your friend buys a bag of 24 party favors and a bag of 16 party favors. She shares them equally among 5 friends. Write an expression to represent the problem.
Answer:
Write the expression in words.
Question 16.
45 + (7 × 8)
Answer:
Add 45 to the product of 7 and 8
Explanation:
Given that the numerical expression is 45 + (7 × 8), so in words, it will be represented as add 45 to the product of 7 and 8
Question 17.
(18 ÷ 2) – 5
Answer:
Divide 18 by 2 and then subtract 5.
Explanation:
Given that the numerical expression is (18 ÷ 2) – 5 so in words, it will be represented as divide 18 by 2 and then subtract 5.
2.4 Evaluate Expressions with Grouping Symbols
Evaluate the expression.
Question 18.
(28 – 14) × (42 ÷ 6)
Answer:
The value of the expression (28 – 14) × (42 ÷ 6) is 98.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So first we will solve the parentheses part which is (28 – 14) × (42 ÷ 6)= 14 × 7. Now we will solve the multiplication part which is 14 × 7= 98 and the result will be 98. So the value of the expression is 98.
Question 19.
6 × [(21 – 9) ÷ 3]
Answer:
The value of the expression 6 × [(21 – 9) ÷ 3] is 24.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So first we will solve the parentheses part which is(21 – 9)= 12. Now we will solve the other parentheses part which is [12 ÷ 3]= 4 and the result will be 4. Now we will solve the multiplication part which is 6 × 4= 24. So the value of the expression is 24.
Question 20.
[(2 × 2) + (10 ÷ 5)] × 4
Answer:
The value of the expression [(2 × 2) + (10 ÷ 5)] × 4 is 32.
Explanation:
By the order of operations, we will perform the addition in the parentheses first and then multiply and divide from left to right. And then we will add and subtract from left to right. So this is performed by the BODMAS rule which stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. So first we will solve the parentheses part which is (2 × 2) + (10 ÷ 5)= 4 + 2 and the result will be 8. Now we will solve the multiplication part which is
8 × 4= 32. So the value of the expression is 32.