Big Ideas Math Answers Grade 5 Chapter 8 Add and Subtract Fractions: See more ideas about fractions at Big Ideas Math Grade 5 Chapter 8 Add and Subtract Fractions. Use mental math to add or subtract fractions. It is necessary for the students to learn the concepts of fractions at the primary level itself. We have to provide the Big Ideas Math Answers Grade 5 Chapter 8 Add and Subtract Fractions in the pdf format so that you can prepare in the offline mode.
Big Ideas Math Book 5th Grade Answer Key Chapter 8 Add and Subtract Fractions
Fractions are one of the most important topics that you need to understand in order to be successful in your career. The topics we have covered in this chapter are Simplest form, Estimate Sums and Differences of Fractions, Find Common Denominators, Add Fractions with Unlike Denominators, Subtract Fractions with Unlike Denominators with a brief explanation. Just tap the links given below to go through the answers.
Lesson: 1 Simplest Form
Lesson: 2 Estimate Sums and Differences of Fractions
- Lesson 8.2 Estimate Sums and Differences of Fractions
- Estimate Sums and Differences of Fractions Homework & Practice 8.2
Lesson: 3 Find Common Denominators
Lesson: 4 Add Fractions with Unlike Denominators
- Lesson 8.4 Add Fractions with Unlike Denominators
- Add Fractions with Unlike Denominators Homework & Practice 8.4
Lesson: 5 Subtract Fractions with Unlike Denominators
- Lesson 8.5 Subtract Fractions with Unlike Denominators
- Subtract Fractions with Unlike Denominators Homework & Practice 8.5
Lesson: 6 Add Mixed Numbers
Lesson: 7 Subtract Mixed Numbers
Lesson: 8 Problem Solving: Fractions
Chapter 8 – Add and Subtract Fractions
- Add and Subtract Fractions Performance Task 8
- Add and Subtract Fractions Activity
- Add and Subtract Fractions Performance Chapter Practice
Lesson 8.1 Simplest Form
Explore and Grow
Use the model to write as many fractions as possible that are equivalent to \(\frac{36}{72}\) but have numerators less than 36 and denominators less than 72.
Which of your fractions has the fewest equal parts? Explain.
Construct Arguments
When might it be helpful to write \(\frac{48}{72}\) as \(\frac{2}{3}\) in a math problem?
Think and Grow: Simplest Form
Key Idea
When the numerator and denominator of a fraction have no common factors other than 1, the fraction is in simplest form. To write a fraction in simplest form, divide the numerator and the denominator by the greatest of their common factors.
Example
simplify \(\frac{6}{8}\) in the simplest form.

Step 1: Find the common factors of 6 and 8.
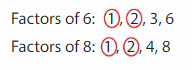
The common factors of 6 and 8 are 1 and 2.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
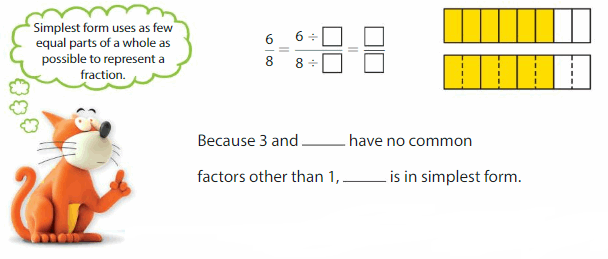
Answer:

Show and Grow
Question 1.
Use the model to write \(\frac{2}{4}\) in simplest form.
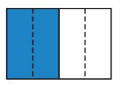
Answer:
Step 1: Find the common factors of 2 and 4.
Factors of 2: 1, 2
Factors of 4: 1, 2, 4
The common factors of 2 and 4 are 1 and 2.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
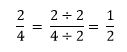

Because 1 and 2 have no common factors other than 1, \(\frac{2}{4}\) is in simplest form.
Question 2.
Write \(\frac{8}{12}\) in simplest form
Answer:
Step 1: Find the common factors of 8 and 12.
Factors of 8: 1, 2, 4, 8
Factors of 12: 1, 2, 3, 4, 6, 12
The common factors of 8 and 12 are 1, 2 and 4.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
![]()
Because 2 and 3 have no common factors other than 1, \(\frac{8}{12}\) is in simplest form.
Apply and Grow: Practice
Use the model to write the fraction in simplest form.
Question 3.
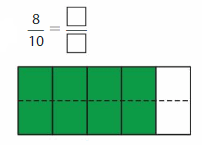
Answer:
Step 1: Find the common factors of 8 and 10.
Factors of 8: 1, 2, 4, 8
Factors of 10: 1, 2, 5, 10
The common factors of 8 and 10 are 1 and 2.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 4 and 5 have no common factors other than 1, \(\frac{8}{10}\) is in simplest form.
Question 4.
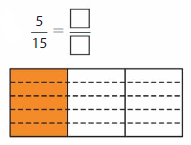
Answer:
Step 1: Find the common factors of 5 and 15.
Factors of 5: 1, 5
Factors of 15: 1, 3, 5,15
The common factors of 5 and 15 are 1 and 5.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 3 have no common factors other than 1, \(\frac{5}{15}\) is in simplest form.
Question 5.
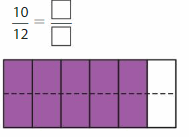
Write the fraction in simplest form.
Answer:
Step 1: Find the common factors of 10 and 12.
Factors of 10: 1, 2, 5, 10
Factors of 12: 1, 2, 3, 4, 6, 12
The common factors of 10 and 12 are 1 and 2.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 5 and 6 have no common factors other than 1, \(\frac{10}{12}\) is in simplest form.
Question 6.
\(\frac{3}{6}\)
Answer:
Step 1: Find the common factors of 3 and 6.
Factors of 3: 1, 3
Factors of 6: 1, 2, 3, 6
The common factors of 3 and 6 are 1 and 3.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 2 have no common factors other than 1, \(\frac{3}{6}\) is in simplest form.
Question 7.
\(\frac{2}{10}\)
Answer:
Step 1: Find the common factors of 2 and 10.
Factors of 2: 1, 2
Factors of 10: 1, 2, 5, 10
The common factors of 2 and 10 are 1 and 2.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 5 have no common factors other than 1, \(\frac{2}{10}\) is in simplest form.
Question 8.
\(\frac{6}{8}\)
Answer:
Step 1: Find the common factors of 6 and 8.
Factors of 6: 1, 2, 3, 6
Factors of 8: 1, 2, 4, 8
The common factors of 6 and 8 are 1 and 2.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 3 and 4 have no common factors other than 1, \(\frac{6}{8}\) is in simplest form.
Question 9.
\(\frac{7}{14}\)
Answer:
Step 1: Find the common factors of 7 and 14.
Factors of 7: 1, 7
Factors of 14: 1, 2, 7, 14
The common factors of 7 and 14 are 1 and 7.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 2 have no common factors other than 1, \(\frac{7}{14}\) is in simplest form.
Question 10.
\(\frac{10}{100}\)
Answer:
Step 1: Find the common factors of 10 and 100.
Factors of 10: 1, 2, 5, 10
Factors of 100: 1, 2, 4, 5, 10, 20, 25, 50, 100
The common factors of 10 and 100 are 1, 2, 5 and 10.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 10 have no common factors other than 1, \(\frac{10}{100}\) is in simplest form.
Question 11.
\(\frac{12}{4}\)
Answer:
Step 1: Find the common factors of 12 and 4.
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 4: 1, 2, 4
The common factors of 12 and 4 are 1, 2 and 4.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 3 and 1 have no common factors other than 1, \(\frac{12}{4}\) is in simplest form.
Question 12.
Three out of nine baseball players are in the outfield. In simplest form, what fraction of the players are in the outfield?

Answer:
Step 1: Find the common factors of 3 and 9.
Factors of 3: 1, 3
Factors of 9: 1, 3, 9
The common factors of 3 and 9 are 1 and 3
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 3 have no common factors other than 1.
Therefore, ![]() players are in the outfield.
players are in the outfield.
Question 13.
YOU BE THE TEACHER
Your friend writes \(\frac{2}{6}\) in simplest form. Is your friend correct? Explain
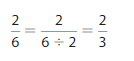
Answer: No, the answer is wrong.
The numerator and the denominator has to divide by the greatest of the common factors. You have divided only the denominator.
Explanation for \(\frac{2}{6}\) in simplest form.
Step 1: Find the common factors of 2 and 6.
Factors of 2: 1, 2
Factors of 6: 1, 2, 3, 6
The common factors of 2 and 6 are 1 and 2.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 3 have no common factors other than 1, \(\frac{2}{6}\) is in simplest form.
Question 14.
Reasoning
The numerator and denominator of a fraction have 1, 2, and 4 as common factors. After you divide the numerator and denominator by 2, the fraction is still not in simplest form. Why?
Answer:
Given that, common factors are 1, 2 and 4
For the fraction to be in the simplest form, the numerator and denominator has to divide by the greatest of the common factors.
Here 4 is the greatest common factor. So, divide both the numerator and denominator by 4 to get the simplest form.
For example 4 and 8
Factors for 4: 1, 2, 4
Factors for 8: 1, 2, 4, 8
common factors: 1, 2 and 4
Simplest form:
Think and Grow: Modeling Real Life
Example
A quarterback passes the ball 45 times during a game. The quarterback completes 35 passes. What fraction of the passes, in simplest form, does the quarterback complete?

Find the number of passes that are not completed by subtracting the pass completions from the total number of passes.
45 – 35 = 10
Write a fraction for the passes the quarterback does not complete.
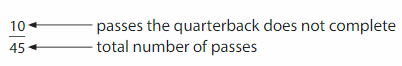
Find common factors of 10 and 45. Then write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.

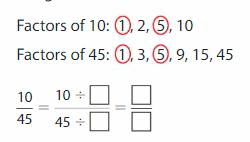
The quarterback does not complete __ of the passes.
Answer:

The quarterback does not complete 2/9 of the passes.
Show and Grow
Question 15.
There are 24 students in your class. Four of the students have blue eyes. What fraction of the class, in simplest form, do not have blue eyes?
Answer:
Given that,
Total no. of students in the class = 24
Students have blue eyes = 4
Students do not have blue eyes = 24 – 4 = 20
Step 1: Find the common factors of 24 and 20.
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 20: 1, 2, 4, 5, 10, 20
The common factors of 24 and 20 are 1, 2 and 4.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 5 and 6 have no common factors other than 1.
Therefore, th of the class do not have blue eyes.
Question 16.
DIG DEEPER!
A student answers 4 out of 12 questions on a test incorrectly. What fraction of the questions, in simplest form, does the student answer incorrectly? Interpret the fraction.
Answer:
Given that,
Total no. of questions = 12
No. of incorrect answers = 4
Step 1: Find the common factors of 12 and 4.
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 4: 1, 2, 4
The common factors of 12 and 4 are 1, 2 and 4.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 3 have no common factors other than 1.
Therefore, of the questions student answered incorrectly.
Lesson 8.1 Simplest Form Homework & Practice 8.1
Use the model to write the fraction in simplest form.
Question 1.
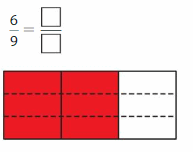
Answer:
Step 1: Find the common factors of 6 and 9.
Factors of 6: 1, 2, 3, 6
Factors of 9: 1, 3, 9
The common factors of 6 and 9 are 1 and 3.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 2 and 3 have no common factors other than 1, is in simplest form.
Question 2.
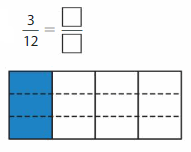
Answer:
Step 1: Find the common factors of 3 and 12.
Factors of 3: 1, 3
Factors of 12: 1, 3, 4, 6, 12
The common factors of 3 and 12 are 1 and 3.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 4 have no common factors other than 1, is in simplest form.
Question 3.
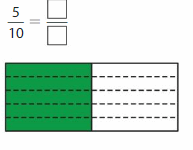
Write the fraction in simplest form
Answer:
Step 1: Find the common factors of 5 and 10.
Factors of 5: 1, 5
Factors of 10: 1, 2, 5, 10
The common factors of 5 and 10 are 1 and 5.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 2 have no common factors other than 1, is in the simplest form.
Question 4.
\(\frac{4}{8}\)
Answer:
Step 1: Find the common factors of 4 and 8.
Factors of 4: 1, 2, 4
Factors of 8: 1, 2, 4, 8
The common factors of 4 and 8 are 1, 2 and 4.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 2 have no common factors other than 1, \(\frac{4}{8}\) is in simplest form.
Question 5.
\(\frac{5}{100}\)
Answer:
Step 1: Find the common factors of 5 and 100.
Factors of 5: 1, 5
Factors of 100: 1, 2, 4, 5, 10, 20, 25, 50, 100
The common factors of 5 and 100 are 1 and 5.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 20 have no common factors other than 1, \(\frac{5}{100}\) is in simplest form.
Question 6.
\(\frac{20}{15}\)
Answer:
Step 1: Find the common factors of 20 and 15.
Factors of 20: 1, 2, 4, 5, 10, 20
Factors of 15: 1, 3, 5, 15
The common factors of 20 and 15 are 1 and 5.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 4 and 3 have no common factors other than 1, \(\frac{20}{15}\) is in simplest form.
Question 7.
There are 18 students in your class. Six of the students pack their lunch. In simplest form, what fraction of the students in your class pack their lunch?

Answer:
Total students in the class = 18
No. of students pack their lunch = 6
Step 1: Find the common factors of 6 and 18.
Factors of 6: 1, 2, 3, 6
Factors of 18: 1, 2, 3, 6, 9, 18
The common factors of 6 and 18 are 1, 2, 3 and 6
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 3 have no common factors other than 1.
Therefore, of the students pack their lunch.
Question 8.
Reasoning
Why do you have to divide a numerator and a denominator by the greatest of their common factors to write a fraction in simplest form?
Answer:
To simplify a fraction to lowest terms, divide both the numerator and the denominator by their common factors. Repeat as needed until the only common factor is 1.
Question 9.
Writing
Explain how you know when a fraction is in simplest form.
Answer:
If the fraction has no common factors other than 1, then it is said to be the simplest form of the fraction.
Question 10.
Open-Ended
Write a fraction in which the numerator and the denominator have 1, 2, 4, and 8 as common factors. Then write the fraction in the simplest form.
Answer:
The fraction in which the numerator and the denominator is .
Step 1: Find the common factors of 8 and 16.
Factors of 8: 1, 2, 4, 8
Factors of 16: 1, 2, 4, 8, 16
The common factors of 8 and 16 are 1, 2, 4 and 8.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 2 have no common factors other than 1.
Question 11.
Modeling Real Life
A flight attendant has visited 30 of the 50 states. What fraction of the states, in simplest form, has he not visited?
Answer:
Given that,
No. of states = 50
A flight attendant has visited 30 states.
The no. of states he has not visited = 50 – 30 = 20
Step 1: Find the common factors of 20 and 50.
Factors of 20: 1, 2, 4, 5, 10, 20
Factors of 50: 1, 2, 5, 10, 25, 50
The common factors of 20 and 50 are 1, 2, 5 and 10.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 2 and 5 have no common factors other than 1.
So the flight attendant has not visited of the states.
Question 12.
DIG DEEPER!
A bin has red, orange, yellow, green, blue, and purple crayons. There are 4 of each color in the bin. In simplest form, what fraction of the crayons are red, orange, yellow, or green?
Answer:
Given that, a bin has 6 colors(red, orange, yellow, green, blue, and purple) of crayons.
There are 4 crayons in the each color = 4 x 6 = 24
If the bin having only 3 colors(red, orange, yellow or green) = 4 x 3 = 12
Step 1: Find the common factors of 12 and 24.
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
The common factors of 12 and 24 are 1, 2, 3, 4, 6 and 12.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 2 have no common factors other than 1.
of the crayons are red, orange, yellow or green.
Review & Refresh
Estimate the sum or difference.
Question 13.
598.44 – 45.61 =
Answer: 550
The number round to 598.44 is 600.
The number round to 45.61 is 50.
600 – 50 = 550
Thus the estimated difference is 550.
Question 14.
93.8 + 4.3 =
Answer: 98
The number round to 93.8 is 94.
The number round to 4.3 is 4.
94 + 4 = 98
Thus the estimated addition is 98.
Lesson 8.2 Estimate Sums and Differences of Fractions
Explore and Grow
Plot \(\frac{7}{12}\), \(\frac{5}{6}\) and \(\frac{1}{10}\) on the number line.
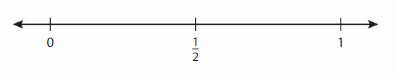
How can you estimate \(\frac{7}{12}\) + \(\frac{5}{6}\) ?
How can you estimate \(\frac{2}{3}\) – \(\frac{1}{10}\)?
Reasoning
Write two fractions that have a sum of about \(\frac{1}{2}\). Then write two fractions that have a difference of about \(\frac{1}{2}\). Explain your reasoning.
Think and Grow: Estimate Sums and Differences
You have used the benchmarks \(\frac{1}{2}\) and 1 to compare fractions. You can use the benchmarks 0, \(\frac{1}{2}\), and 1 to estimate sums and differences of fractions.
Example
Estimate \(\frac{1}{6}\) + \(\frac{5}{8}\)
Step 1: Use a number line to estimate each fraction.

Step 2: Estimate the sum.
An estimate of \(\frac{1}{6}\) + \(\frac{5}{8}\) is __ + __ = ___
Example
Estimate \(\frac{9}{10}\) – \(\frac{2}{5}\).

Show and Grow
Estimate the sum or difference
Question 1.
\(\frac{1}{3}\) + \(\frac{11}{12}\)
Answer:
Step 1: Estimate each fraction.
is between 0 and
, but is closer to
is between
and 1, but is closer to 1
Step 2: Estimate the sum.
An estimate of \(\frac{1}{3}\) + \(\frac{11}{12}\) is + 1 =
Question 2.
\(\frac{3}{5}\) + \(\frac{5}{6}\)
Answer:
Step 1: Estimate each fraction
is between
and 1 , but is closer to
is between
and 1, but is closer to 1
Step 2: Estimate the sum.
An estimate of \(\frac{3}{5}\) + \(\frac{5}{6}\) is + 1 =
Question 3.
\(\frac{15}{16}\) – \(\frac{7}{8}\)
Answer:
Step 1: Use mental math to estimate each fraction.
is about
Think : The numerator is about the same as the denominator.
is about
Think : The numerator is about the same as the denominator.
Step 2: Estimate the difference.
An estimate of –
is 1 – 1 = 0.
Apply and Grow: Practice
Estimate the sum or difference.
Question 4.
\(\frac{1}{6}\) + \(\frac{3}{5}\)
Answer:
Step 1: Estimate each fraction.
is between 0 and
, but is closer to 0.
is between
and 1, but is closer to
.
Step 2: Estimate the sum.
An estimate of \(\frac{1}{6}\) + \(\frac{3}{5}\) = 0 + =
Question 5.
\(\frac{4}{5}\) – \(\frac{5}{12}\)
Answer:
Step 1: Use mental math to estimate each fraction.
is about
Think: The numerator is about the same as the denominator.
is about
Think: The numerator is about half of the denominator.
Step 2: Estimate the difference.
An estimate of –
is 1 –
=
Question 6.
\(\frac{13}{16}\) + \(\frac{5}{6}\)
Answer:
Step 1: Estimate each fraction.
is between
and 1, but is closer to 1.
is between
and 1, but is closer to 1.
Step 2: Estimate the sum.
An estimate of \(\frac{13}{16}\) + \(\frac{5}{6}\) = 1+1 = 2
Question 7.
\(\frac{3}{6}\) – \(\frac{1}{8}\)
Answer:
Step 1: Use mental math to estimate each fraction.
is about
Think: The numerator is about half of the denominator.
is about
Think: The numerator is near to zero.
Step 2: Estimate the difference.
An estimate of –
is
– 0 =
.
Question 8.
\(\frac{1}{14}\) + \(\frac{98}{100}\)
Answer:
Step 1: Estimate each fraction.
is closer to 0
is closer to 1.
Step 2: Estimate the sum.
An estimate of \(\frac{1}{14}\) + \(\frac{98}{100}\) = 0 +1 = 1
Question 9.
\(\frac{11}{12}\) – \(\frac{1}{8}\)
Answer:
Step 1: Use mental math to estimate each fraction.
is about
Think: The numerator is about the same as the denominator.
is about
Think: The numerator is near to zero.
Step 2: Estimate the difference.
An estimate of –
is 1 – 0 = 1.
Question 10.
You walk \(\frac{1}{10}\) mile to your friend’s house and then you both walk \(\frac{2}{5}\) mile. Estimate how much farther you walk with your friend than you walk alone.

Answer:
To find how much farther I walk with my friend than I walk alone, subtract the distance that I walk alone from we both walk.
Step 1: Use mental math to estimate each fraction.
is about____
Think: The numerator is near to zero.
is about____
Think: The numerator is about half of the denominator.
Step 2: Estimate the difference.
An estimate of –
=
– 0 =
So the distance I walk with my friend than I walk alone is mile.
Question 11.
A carpenter has two wooden boards. One board is \(\frac{3}{4}\) foot long and the other board is \(\frac{1}{6}\) foot long. To determine whether the total length of the boards is 1 foot, should the carpenter use an estimate, or is an exact answer required? Explain.
Answer:
Given,
A carpenter has two wooden boards. One board is \(\frac{3}{4}\) foot long and the other board is \(\frac{1}{6}\) foot long.
\(\frac{3}{4}\) + \(\frac{1}{6}\)
The fractions have unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCM = 12
\(\frac{3}{4}\) × \(\frac{3}{3}\) = \(\frac{9}{12}\)
\(\frac{1}{6}\) × \(\frac{2}{2}\) = \(\frac{2}{12}\)
\(\frac{9}{12}\) + \(\frac{2}{12}\) = \(\frac{11}{12}\)
\(\frac{11}{12}\) is approximately equal to 1 foot.
Question 12.
Number Sense
A fraction has a numerator of 1 and a denominator greater than 4. Is the fraction closer to 0, \(\frac{1}{2}\), or 1? Explain.
Answer:
Given,
A fraction has a numerator of 1 and a denominator greater than 4.
\(\frac{1}{4}\) = 0.25
If the denominator is greater than 4. Let’s consider 8.
\(\frac{1}{8}\) = 0.125
The fraction will be close to 0.
Think and Grow: Modeling Real Life
Example
In the human body, the small intestine is about 20\(\frac{1}{12}\) feet long. The large intestine is about 4\(\frac{5}{6}\) feet long. About how long are the intestines in the human body?
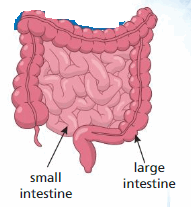
To find the total length of the intestines, estimate 20\(\frac{1}{12}\) + 4\(\frac{5}{6}\).
Step 1: Use mental math to round each mixed number to the nearest whole number.

Answer:

Show and Grow
Question 13.
A bullfrog jumps 5\(\frac{11}{12}\) feet. A leopard frog jumps 4\(\frac{1}{3}\) feet. About how much farther does the bullfrog jump than the leopard frog?
Answer:
Step 1: Use mental math to round each mixed number to the nearest whole number.
5 is about,
is closer to 1 than 0.
4 is about,
is closer to 0 than 1.
Step 2: Estimate the difference
An estimate of 5 – 4
= 1 – 0 = 1
So, bullfrog jumps 1 feet farther than the leopard frog.
Question 14.
DIG DEEPER!
A cell phone has 32 gigabytes of storage. The amounts of storage used by photos, songs, and apps are shown. About how many gigabytes of storage are left?
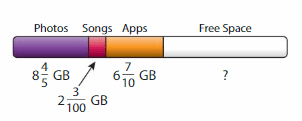
Answer:
Given that,
No. of gigabytes of storage in cellphone = 32
Step 1: Use mental math to round each mixed number to the nearest whole number.
Photos —> 8 is about,
is closer to 1 than 0
Songs —> 2 is about,
is closer to 0 than 1
Apps —> 6 is about,
is closer to 1 than 0
Step 2: Storage left in the phone = Total storage – storage(photos + songs + apps)
= 32 – (1 + 0 + 1)
Therefore, storage left = 30 gigabytes.
Question 15.
DIG DEEPER!
Use two different methods to estimate how many cups of nut medley the recipe makes. Which estimate do you think is closer to the actual answer? Explain.

Answer:
1 \(\frac{3}{8}\) + \(\frac{5}{8}\) + 2 \(\frac{1}{3}\)
First add the whole numbers
1 + 2 = 3
\(\frac{3}{8}\) + \(\frac{5}{8}\) + \(\frac{1}{3}\)
1 \(\frac{1}{3}\)
3 + 1 \(\frac{1}{3}\) = 4 \(\frac{1}{3}\)
The fraction is 4 \(\frac{1}{3}\)
4 is equal to the actual answer.
Estimate Sums and Differences of Fractions Homework & Practice 8.2
Estimate the sum or difference
Question 1.
\(\frac{11}{12}\) – \(\frac{5}{6}\)
Answer:
Step 1: Use mental math to estimate each fraction.
is about
Think : The numerator is about the same as the denominator.
is about
Think : The numerator is about same as the denominator.
Step 2: Estimate the difference.
An estimate of –
is 1 – 1 = 0.
Question 2.
\(\frac{17}{20}\) + \(\frac{13}{20}\)
Answer:
Step 1: Estimate each fraction.
is between
and 1, but is closer to 1.
is between
and 1, but is closer to
.
Step 2: Estimate the sum.
An estimate of \(\frac{17}{20}\) + \(\frac{13}{20}\) = 1 + =
.
Question 3.
\(\frac{3}{8}\) – \(\frac{1}{6}\)
Answer:
Step 1: Use mental math to estimate each fraction.
is about
Think : The numerator is about half of the denominator.
is about
Think : The numerator is near to zero.
Step 2: Estimate the difference.
An estimate of –
is
– 0 =
.
Question 4.
\(\frac{7}{12}\) + \(\frac{2}{5}\)
Answer:
Step 1: Estimate each fraction.
is between
and 1, but is closer to
.
is between 0 and
, but is closer to
.
Step 2: Estimate the sum.
An estimate of \(\frac{7}{12}\) + \(\frac{2}{5}\) = +
= 1.
Question 5.
\(\frac{4}{5}\) – \(\frac{7}{12}\)
Answer:
Step 1: Use mental math to estimate each fraction.
is about
Think: The numerator is about the same as the denominator.
is about
Think: The numerator is about half of the denominator.
Step 2: Estimate the difference.
An estimate of –
is 1 –
=
Question 6.
\(\frac{1}{5}\) + 1\(\frac{10}{21}\)
Answer:
Step 1: Use mental math to round each mixed number to the nearest whole number.
\(\frac{1}{5}\) is closer to 0
1\(\frac{10}{21}\) is close to 1.
Step 2: Estimate the sum.
An estimate of \(\frac{1}{5}\) + 1\(\frac{10}{21}\)
= 0 + 1 = 1
Question 7.
3\(\frac{5}{8}\) – \(\frac{1}{10}\)
Answer:
Step 1: Use mental math to round each mixed number to the nearest whole number.
3 is about,
is closer to 1 than 0
is near to 0
Step 2: Estimate the difference
An estimate of 3 –
= 1 – 0 = 1.
Question 8.
6\(\frac{1}{3}\) + 2\(\frac{4}{6}\)
Answer:
Step 1: Use mental math to round each mixed number to the nearest whole number.
\(\frac{1}{3}\) is close to 0 than 1.
\(\frac{4}{6}\) is to 1 than 0.
Step 2: Estimate the sum
An estimate of 6\(\frac{1}{3}\) is 6.
An estimate of 2\(\frac{4}{6}\) is 3.
6 + 3 = 9
Question 9.
5\(\frac{7}{8}\) – 4\(\frac{49}{100}\)
Answer:
Step 1: Use mental math to round each mixed number to the nearest whole number.
5 is about,
is closer to 1 than 0
4 is about,
is closer to 0 than 1
Step 2: Estimate the difference
An estimate of 5 – 4
= 1 – 0 = 1.
Question 10.
You make a bag of trail mix with \(\frac{2}{3}\) cup of raisins and \(\frac{9}{8}\) cups of peanuts. About how much trail mix do you make?
Answer:
Raisins = cups
Peanuts = cups
Step 1: Estimate each fraction.
is between
and 1, but is closer to
.
is closer to 1.
Step 2: Estimate the sum.
An estimate of \(\frac{2}{3}\) + \(\frac{9}{8}\) = + 1 =
.
So trail mix = .
Question 11.
You have \(\frac{2}{3}\) cup of flour in a bin and \(\frac{7}{8}\) cup of flour in a bag. To determine whether you have enough flour for a recipe that needs 1\(\frac{3}{4}\) cups of flour, should you use an estimate, or is an exact answer required? Explain.
Answer:
Given,
You have \(\frac{2}{3}\) cup of flour in a bin and \(\frac{7}{8}\) cup of flour in a bag.
\(\frac{2}{3}\) + \(\frac{7}{8}\) = 1 \(\frac{13}{24}\)
Th estimated fraction of 1 \(\frac{13}{24}\) is 1\(\frac{3}{4}\)
Question 12.
Writing
Explain how you know \(\frac{9}{10}\) – \(\frac{3}{5}\) is about \(\frac{1}{2}\).
Answer:
Step 1: Use mental math to estimate each fraction.
is about
Think: The numerator is about the same as the denominator.
is about
Think : The numerator is about half of the denominator.
Step 2: Estimate the difference.
An estimate of –
is 1 –
=
.
Question 13.
Precision
Your friend says \(\frac{5}{8}\) + \(\frac{7}{12}\) is about 2. Find a closer estimate. Explain why your estimate is closer.
Answer:
\(\frac{5}{8}\) + \(\frac{7}{12}\) = 1 \(\frac{5}{24}\)
\(\frac{5}{24}\) is closer to 1 than 0.
1 \(\frac{5}{24}\) is about 2.
Question 14.
Modeling Real Life
About how much taller is Robot A than Robot B?

Answer:
Step 1: Use mental math to round each mixed number to the nearest whole number.
1 is about,
is closer to 1 than 0.
1 is about,
is closer to 0 than 1.
Step 2: Estimate the difference
An estimate of 1 – 1
= 1 – 0 = 1.
Robot A is 1 meter taller than Robot B.
Question 15.
Modeling Real Life
A class makes a paper chain that is 5\(\frac{7}{12}\) feet long. The class adds another 3\(\frac{5}{6}\) feet to the chain. About how long is the chain now?

Answer:
Step 1: Use mental math to round each mixed number to the nearest whole number.
5 is about,
is closer to 1 than 0.
3 is about,
is closer to 1 than 0.
Step 2: Estimate the sum
An estimate of 5 + 3
= 1 + 1 = 2
Therefore, the chain is now 2 feet long.
Review & Refresh
Find the product. Check whether your answer is reasonable.
Question 16.
509 × 5 = ___
Answer:
The number 509 round to hundred is 500.
500 × 5 = 2500
509 × 5 = 2545
So the answer is reasonable.
Question 17.
7,692 × 6 = ___
Answer:
The number 7692 round to hundred is 7700.
7700 × 6 = 46200
7,692 × 6 = 46152
So the answer is reasonable.
Question 18.
31,435 × 7 = ___
Answer:
The number 31435 round to hundred is 31,400.
31,400 × 7 = 219800
31,435 × 7 = 220045
So the answer is reasonable.
Lesson 8.3 Find Common Denominators
Explore and Grow
You cut a rectangular pan of vegetable lasagna into equal-sized pieces. You serve \(\frac{1}{2}\) of the lasagna to a large table and \(\frac{1}{3}\) of the lasagna to a small table. Draw a diagram that shows how you cut the lasagna.
What fraction of the lasagna does each piece represent? How does the denominator of the fraction compare to the denominators of \(\frac{1}{2}\) and \(\frac{1}{3}\) ?
Reasoning
Is there another way you can cut the lasagna? Explain your reasoning.
Think and Grow: Find Common Denominators
Key Idea
Fractions that have the same denominator are said to have a common denominator. You can find a common denominator either by finding a common multiple of the denominators or by finding the product of the denominators.
Example
Use a common denominator to write equivalent fractions for \(\frac{1}{2}\) and \(\frac{5}{8}\).
List multiples of the denominators.

Answer:

Example
Use a common denominator to write equivalent fractions for \(\frac{2}{3}\) and \(\frac{1}{4}\). Use the product of the denominators: 3 × 4 = __.
Write equivalent fractions with denominators of 12.
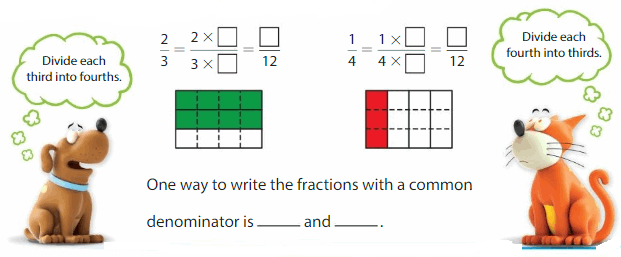
Answer:
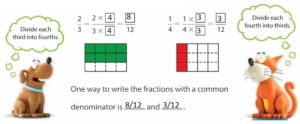
Show and Grow
Use a common denominator to write an equivalent fraction for each fraction.
Question 1.
\(\frac{2}{3}\) and \(\frac{1}{6}\)
Answer:
Use the product of the denominators : 3 6 = 18
Write equivalent fractions with denominators of 18
Therefore, equivalent fractions are and
.
Question 2.
\(\frac{5}{6}\) and \(\frac{3}{4}\)
Answer:
Step 1: Use the product of the denominators : 6 4 = 24
Step 2: Write equivalent fractions with denominators of 24
Therefore, equivalent fractions are and
.
Apply and Grow: Practice
Use a common denominator to write an equivalent fraction for each fraction.
Question 3.
\(\frac{2}{3}\) and \(\frac{5}{6}\)
Answer:
Step 1: Use the product of the denominators : 3 6 = 18
Step 2: Write equivalent fractions with denominators of 18
Therefore, equivalent fractions are and
.
Question 4.
\(\frac{3}{4}\) and \(\frac{1}{2}\)
Answer:
Step 1: Use the product of the denominators : 4 2 = 8
Step 2: Write equivalent fractions with denominators of 8
Therefore, equivalent fractions are and
.
Question 5.
\(\frac{5}{9}\) and \(\frac{2}{3}\)
Answer:
Step 1: Use the product of the denominators: 9 3 = 27
Step 2: Write equivalent fractions with denominators of 27
Therefore, equivalent fractions are and
.
Question 6.
\(\frac{8}{21}\) and \(\frac{3}{7}\)
Answer:
Step 1: Use the product of the denominators: 21 7 = 147
Step 2: Write equivalent fractions with denominators of 147
Therefore, equivalent fractions are and
.
Question 7.
\(\frac{1}{5}\) and \(\frac{1}{2}\)
Answer:
Step 1: Use the product of the denominators: 5 2 = 10
Step 2: Write equivalent fractions with denominators of 10
Therefore, equivalent fractions are and
.
Question 8.
\(\frac{3}{4}\) and \(\frac{1}{6}\)
Answer:
Step 1: Use the product of the denominators: 4 6 = 24
Step 2: Write equivalent fractions with denominators of 24
Therefore, equivalent fractions are and
.
Question 9.
\(\frac{3}{7}\) and \(\frac{2}{9}\)
Answer:
Step 1: Use the product of the denominators: 7 9 = 63
Step 2: Write equivalent fractions with denominators of 63
Therefore, equivalent fractions are and
.
Question 10.
\(\frac{3}{8}\) and \(\frac{5}{11}\)
Answer:
Step 1: Use the product of the denominators: 8 11 = 88
Step 2: Write equivalent fractions with denominators of 88
Therefore, equivalent fractions are and
.
Question 11.
You walk your dog \(\frac{3}{4}\) mile on Saturday and \(\frac{5}{8}\) mile on Sunday. Use a common denominator to write an equivalent fraction for each fraction.

Answer:
Step 1: Use the product of the denominators: 4 8 = 32
Step 2: Write equivalent fractions with denominators of 32
Dog walk on Saturday, equivalent fraction =
Dog walk on Sunday, equivalent fraction =
Question 12.
Writing
Explain how to use the models to find a common denominator for \(\frac{1}{2}\) and \(\frac{3}{5}\). Then write an equivalent fraction for each fraction.

Answer:
Initially find the product of the denominators and that product value is the denominator for both fractions.
Step 1: Use the product of the denominators: 2 5 = 10
Step 2: Write equivalent fractions with denominators of 10
Therefore, equivalent fractions are and
.
Question 13.
Number Sense
Which pairs of fractions are equivalent to \(\frac{1}{2}\) and \(\frac{2}{3}\) ?
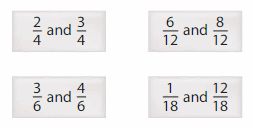
Answer:
and
and
These two fractions are equivalent to \(\frac{1}{2}\) and \(\frac{2}{3}\).
Think and Grow: Modeling Real Life
Example
You and your friend make woven key chains. Your key chain is \(\frac{2}{4}\) foot long. Your friend’s is \(\frac{3}{6}\) foot long. Are the key chains the same length?

Use a common denominator to write equivalent fractions for the lengths of the key chains. Use the product of the denominators.
![]()
Write equivalent fractions with denominators of 24.
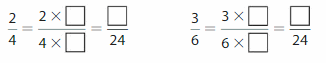
Compare the lengths of the key chains.
So, the key chains __ the same length.
Answer:
4 × 6 = 24
Write equivalent fractions with denominators of 24.
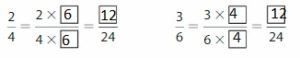
So, the key chains has the same length.
Show and Grow
Question 14.
Your hamster weighs \(\frac{13}{16}\) ounce. Your friend’s hamster weighs \(\frac{6}{8}\) ounce. Do the hamsters weigh the same amount?

Answer:
Use a common denominator to write equivalent fractions for the hamsters weight.
Step 1: Use the product of the denominators: 16 8 = 128
Step 2: Write equivalent fractions with denominators of 128
Hamsters weigh the different amount. One is ounce and the other one is
ounce.
Question 15.
DIG DEEPER!
You have three vegetable pizzas of the same size. One has 4 equal slices. The second has 8 equal slices. The third has 6 equal slices. You cut the pizzas until all of them have the same number of slices. How many slices does each pizza have?
Answer:
Given,
You have three vegetable pizzas of the same size.
One has 4 equal slices. The second has 8 equal slices.
The third has 6 equal slices. You cut the pizzas until all of them have the same number of slices.
4 + 6 + 8 = 18
one has \(\frac{4}{18}\)
second has \(\frac{6}{18}\)
Third has \(\frac{8}{18}\)
Total there are 18 slices.
Find Common Denominators Homework & Practice 8.3
Use a common denominator to write an equivalent fraction for each fraction.
Question 1.
\(\frac{1}{2}\) and \(\frac{3}{8}\)
Answer:
Step 1: Use the product of the denominators: 2 8 = 16
Step 2: Write equivalent fractions with denominators of 16
Therefore, equivalent fractions are and
.
Question 2.
\(\frac{7}{9}\) and \(\frac{2}{3}\)
Answer:
Step 1: Use the product of the denominators: 9 3 = 27
Step 2: Write equivalent fractions with denominators of 27.
Therefore, equivalent fractions are and
.
Question 3.
\(\frac{5}{6}\) and \(\frac{1}{2}\)
Answer:
Step 1: Use the product of the denominators: 6 2 = 12
Step 2: Write equivalent fractions with denominators of 12.
Therefore, equivalent fractions are and
.
Question 4.
\(\frac{3}{4}\) and \(\frac{5}{16}\)
Answer:
Step 1: Use the product of the denominators: 4 16 = 64
Step 2: Write equivalent fractions with denominators of 64.
Therefore, equivalent fractions are and
.
Question 5.
\(\frac{18}{24}\) and \(\frac{5}{6}\)
Answer:
Step 1: Use the product of the denominators: 24 6 = 144
Step 2: Write equivalent fractions with denominators of 144.
Therefore, equivalent fractions are and
.
Question 6.
\(\frac{1}{3}\) and \(\frac{1}{5}\)
Answer:
Step 1: Use the product of the denominators: 3 5 = 15
Step 2: Write equivalent fractions with denominators of 15.
Therefore, equivalent fractions are and
.
Question 7.
\(\frac{3}{5}\) and \(\frac{4}{7}\)
Answer:
Step 1: Use the product of the denominators: 5 7= 35
Step 2: Write equivalent fractions with denominators of 35.
Therefore, equivalent fractions are and
.
Question 8.
\(\frac{5}{8}\) and \(\frac{2}{9}\)
Answer:
Step 1: Use the product of the denominators: 8 9 = 72
Step 2: Write equivalent fractions with denominators of 72.
Therefore, equivalent fractions are and
.
Question 9.
A mint plant grows \(\frac{7}{8}\) inch in 1 week and \(\frac{13}{16}\) inch the next week. Use a common denominator to write an equivalent fraction for each fraction.
Answer:
Step 1: Use the product of the denominators : 8 16 = 128
Step 2: Write equivalent fractions with denominators of 128.
Therefore, equivalent fractions are and
.
Question 10.
Which One Doesn’t Belong? Which pair of fractions is not equivalent to \(\frac{2}{5}\) and \(\frac{1}{10}\)?
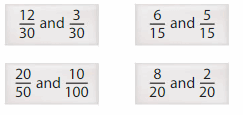
Answer:
So, and
is not equivalent to \(\frac{2}{5}\) and \(\frac{1}{10}\) and remaining all the pairs are equivalent.
Question 11.
YOU BE THE TEACHER
Your friend says she used a common denominator to find fractions equivalent to \(\frac{2}{3}\) and \(\frac{8}{9}\). Is your friend correct? Explain.
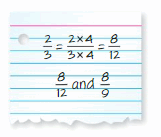
Answer:
No, she is wrong because 9 and 12 are not common denominators.
Step 1: Use the product of the denominators : 3 9 = 27
Step 2: Write equivalent fractions with common denominator of 27.
Therefore, equivalent fractions are and
.
Question 12.
Modeling Real Life
Some friends spend \(\frac{1}{3}\) hour collecting sticks and \(\frac{5}{6}\) hour building a fort. Do they spend the same amount of time on each? Explain.

Answer:
No, they can not spend the same time on each because is not equivalent to
.
is equivalent to
.
Question 13.
DIG DEEPER!
Use a common denominator to write an equivalent fraction for each fraction. Which two students are the same distance from the school? Are they closer to or farther from the school than the other student?

Answer:
Step 1: Use the LCM of the denominators. LCM of 12, 8 and 6 = 24
Step 2: Write equivalent fractions with common denominator of 24.
Student A –>
Student B –>
Student C –>
Therefore, student A and student C are the same distance from the school i.e. mile.
They are closer to student B.
Review & Refresh
Find the value of the expression.
Question 14.
102
Answer: 100
Question 15.
8 × 104
Answer: 80,000
Question 16.
6 × 103
Answer: 6000
Question 17.
9 × 105
Answer: 9,00,000
Lesson 8.4 Add Fractions with Unlike Denominators
Use a model to find the sum.

Explain how you can use a model to add fifths and tenths.
Construct Arguments
How can you add two fractions with unlike denominators without using a model? Explain why your method makes sense.
Think and Grow: Add Fractions with Unlike Denominators
You can use equivalent fractions to add fractions that have unlike denominators.
Example
Find \(\frac{1}{4}\) + \(\frac{3}{8}\)
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 8 is a multiple of 4, so rewrite \(\frac{1}{4}\) with a denominator of 8.
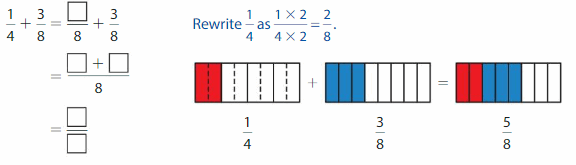
Answer:
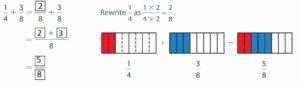
Example
Find \(\frac{7}{8}\) + \(\frac{1}{6}\) Estimate __
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 8 is not a multiple of 6, so rewrite each fraction with a denominator of 8 × 6 = 48.

Answer:

Show and Grow
Add.
Question 1.

Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 6 is a multiple of 3, so rewrite it with a denominator of 6.
Rewrite as
=
+
=
+
= or
Question 2.
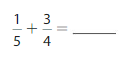
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 5 is not a multiple of 4, so rewrite each fraction with a denominator of 5 4 = 20
Rewrite as
=
and
as
=
+
=
+
=
Question 3.
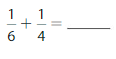
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 6 is not a multiple of 4, so rewrite each fraction with a denominator of 6 4 = 24
Rewrite as
=
and
as
=
+
=
+
= or
Apply and Grow: Practice
Add.
Question 4.
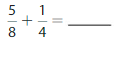
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 8 is a multiple of 4, so rewrite it with a denominator of 8.
Rewrite as
=
+
=
+
=
Question 5.
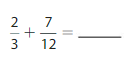
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 12 is a multiple of 3, so rewrite it with a denominator of 12.
Rewrite as
=
+
=
+
= or
Question 6.
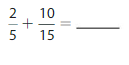
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 15 is a multiple of 5 , so rewrite it with a denominator of 15.
Rewrite as
=
+
=
+
=
Question 7.

Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 8 is not a multiple of 6, so rewrite each fraction with a denominator of 8 × 6 = 48.
Rewrite as
=
and
as
=
+
=
+
= or
Question 8.

Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 12 is not a multiple of 5, so rewrite each fraction with a denominator of 12 × 5 = 60.
Rewrite as
=
and
as
=
+
=
+
=
Question 9.
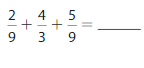
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 9 is a multiple of 3 , so rewrite it with a denominator of 9.
Rewrite as
=
+
+
=
+
+
=
Question 10.
Your friend buys \(\frac{1}{8}\) pound of green lentils and \(\frac{3}{4}\) pound of brown lentils. What fraction of a pound of lentils does she buy?

Answer:
Given that,
pound of green lentils =
Pound of brown lentils =
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 8 is a multiple of 4, so rewrite with a denominator of 8.
Rewrite as
=
Pound of lentils = +
= +
Fraction of pound of lentils =
Question 11.
Reasoning
Newton and Descartes find \(\frac{1}{2}\) + \(\frac{1}{6}\). Newton says the sum is \(\frac{4}{6}\). Descartes says the sum is \(\frac{2}{3}\). Who is correct? Explain.
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
+
Think: 6 is a multiple of 2, so rewrite with a denominator of 6.
Rewrite as
=
+
=
+
= or
Therefore, both Newton and Descartes answers are correct.
Question 12.
DIG DEEPER!
Write two fractions that have a sum of 1 and have different denominators.
Answer:
\(\frac{1}{2}\) + \(\frac{3}{6}\)
= \(\frac{1}{2}\) × \(\frac{3}{3}\) + \(\frac{3}{6}\)
= \(\frac{3}{6}\) + \(\frac{3}{6}\)
= \(\frac{6}{6}\)
= 1
Think and Grow: Modeling Real Life
Example
About \(\frac{17}{15}\) of Earth’s surface is covered by ocean water.
About \(\frac{3}{100}\) of Earth’s surface is covered by other water resources.

About how much of Earth’s surface is covered by water?

Answer:

Show and Grow
Question 13.
The George Washington Bridge links Manhattan, NY, to FortLee, NJ. The part of the bridge in New Jersey is about \(\frac{1}{2}\) mile long. The part in New York is about \(\frac{2}{5}\) mile long. About how long is the George Washington Bridge?

Answer:
Given that,
New Jersey bridge = \(\frac{1}{2}\) mile long
New York bridge = \(\frac{2}{5}\) mile long
Add and
to find how long is the George Washington Bridge
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 5 is not a multiple of 2, so rewrite each fraction with a denominator of 5 2 = 10
Rewrite as
=
and
as
=
+
=
+
=
So, George Washington Bridge is about mile long.
Question 14.
DIG DEEPER!
Your goal is to practice playing the saxophone for at least 2 hours in 1 week. Do you reach your goal? Explain.

Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
+
+
Think: Rewrite the denominators as 4 2
3 = 24
Rewrite as
=
as
=
as
=
+
+
=
+
+
= or
Total practice time in a week = = 1.91 hours
So, goal does not reached.
Add Fractions with Unlike Denominators Homework & Practice 8.4
Add
Question 1.
\(\frac{1}{9}\) + \(\frac{2}{3}\) = ___
Answer:
+
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 9 is a multiple of 3, so rewrite it with a denominator of 9
Rewrite as
=
+
=
+
=
\(\frac{1}{9}\) + \(\frac{2}{3}\) =
Question 2.
\(\frac{1}{2}\) + \(\frac{3}{4}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 4 is a multiple of 2, so rewrite it with a denominator of 4
Rewrite as
+
=
+
=
\(\frac{1}{2}\) + \(\frac{3}{4}\) =
Question 3.
\(\frac{4}{6}\) + \(\frac{5}{12}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 12 is a multiple of 6, so rewrite it with a denominator of 12
Rewrite as
=
+
=
+
=
\(\frac{4}{6}\) + \(\frac{5}{12}\) =
Question 4.
\(\frac{1}{3}\) + \(\frac{1}{4}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 4 is not a multiple of 3, so rewrite each fraction with a denominator of 4 3 = 12
Rewrite as
=
and
as
=
+
=
+
=
\(\frac{1}{3}\) + \(\frac{1}{4}\) =
Question 5.
\(\frac{3}{2}\) + \(\frac{4}{5}\) = __
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 5 is not a multiple of 2, so rewrite each fraction with a denominator of 5 2 = 10
Rewrite as
=
and
as
=
+
=
+
=
\(\frac{3}{2}\) + \(\frac{4}{5}\) =
Question 6.
\(\frac{6}{8}\) + \(\frac{9}{10}\) + \(\frac{1}{8}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 10 is not a multiple of 8, so rewrite each fraction with a denominator of 10 8 = 80
Rewrite as
=
as
=
as
=
+
+
=
+
+
=
\(\frac{6}{8}\) + \(\frac{9}{10}\) + \(\frac{1}{8}\) =
Question 7.
You use beads to make a design. Of the beads, \(\frac{1}{3}\) are red and \(\frac{1}{6}\) are blue. The rest are white.What fraction of the beads are red or blue?
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 6 is a multiple of 3, so rewrite it with a denominator of 6
Rewrite as
=
+
=
+
=
The fraction of beads are red or blue = =
Rest are white =
Question 8.
YOU BE THE TEACHER
Your friend says the sum of \(\frac{1}{5}\) and \(\frac{9}{10}\) is \(\frac{10}{15}\). Is your friend correct? Explain.
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 10 is a multiple of 5, so rewrite it with a denominator of 10
Rewrite as
=
+
=
+
=
Therefore, the sum of \(\frac{1}{5}\) and \(\frac{9}{10}\) is .
So, my friend answer is wrong.
Question 9.
Reasoning
Which expressions are equal to \(\frac{14}{15}\)?
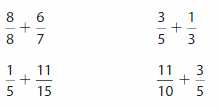
Answer:
+
and
+
are equal to \(\frac{14}{15}\) and these two expressions only having denominator of 15.
Question 10.
Modeling Real Life
There are 100 senators in the 115th Congress. Democrats make up of the senators, and Republicans make up \(\frac{13}{25}\) of the 25 senators. The rest are Independents. What fraction of the senators are Democrat or Republican?
Answer:
Given,
There are 100 senators in the 115th Congress.
Democrats make up of the senators, and Republicans make up \(\frac{13}{25}\) of the 25 senators.
\(\frac{100}{115}\) + \(\frac{13}{25}\)
= \(\frac{100}{115}\) × \(\frac{5}{5}\) + \(\frac{13}{25}\) × \(\frac{23}{23}\)
= \(\frac{799}{575}\)
= 1 \(\frac{224}{575}\)
Question 11.
Modeling Real Life
Your friend needs 1 cup of homemade orange juice. He squeezes \(\frac{1}{2}\) cup of orange juice from one orange and \(\frac{3}{8}\) cup from another orange. Does your friend need to squeeze another orange? Explain.
Answer:
+
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 8 is a multiple of 2, so rewrite it with a denominator of 8
Rewrite as
=
+
=
+
=
Juice from 2 oranges =
My friend needs 1 cup of orange juice = 1 – =
So, my friend needs to squeeze cup from another orange.
Question 12.
DIG DEEPER!
Of all the atoms in caffeine, \(\frac{1}{12}\) are oxygen atoms, \(\frac{1}{6}\) are nitrogen atoms, and \(\frac{1}{3}\) are carbon atoms. The rest of the atoms are hydrogen. What fraction of the atoms in caffeine are oxygen, nitrogen, or hydrogen?
Answer:
From the given information, hydrogen atoms = 1- ( +
+
) =
+
+
= ?
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 12 is a multiple of 6, so rewrite it with a denominator of 12
Rewrite as
=
+
+
=
+
+
=
=
So of the atoms in caffeine are oxygen, nitrogen, or hydrogen.
Review & Refresh
Use properties to find the sum or product.
Question 13.
5 × 84
Answer: 420
Explanation:
We can find the product by using the distributive property.
5 × 84 = 5 × (80 + 4)
= (5 × 80) + (5 × 4)
= 400 + 20
= 420
Question 14.
521 + 0 + 67
Answer: 588
Explanation:
We can find the sum of the given expression using the additive identity.
521 + 0 + 67 = 521 + 67
= 588
Question 15.
25 × 8 × 4
Answer: 800
Explanation:
25 × 8 × 4
= 25 × 32
= 800
Lesson 8.5 Subtract Fractions with Unlike Denominators
Explore and Grow
Use a model to find the difference.
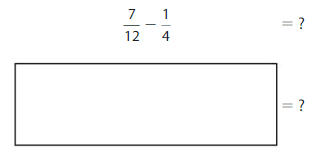
Explain how you can use a model to subtract fourths from twelfths.
Construct Arguments
How can you subtract two fractions with unlike denominators without using a model? Explain why your method makes sense.
Think and Grow: Subtract Fractions with Unlike Denominators
You can use equivalent fractions to subtract fractions that have unlike denominators.
Example
Find \(\frac{9}{10}\) – \(\frac{1}{2}\).
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 10 is a multiple of 2, so rewrite \(\frac{1}{2}\) with a denominator of 10.
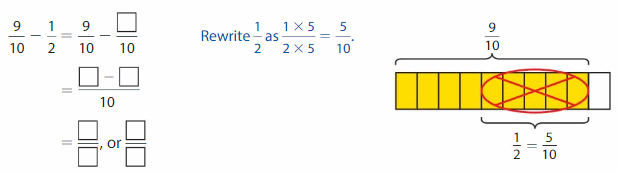
Answer:

Example
Find \(\frac{4}{3}\) – \(\frac{1}{4}\). Estimate _____
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 4 is not a multiple of 3, so rewrite each fraction with a denominator of 3 × 4 = 12.
Show and Grow
Subtract.
Question 1.
\(\frac{1}{2}\) – \(\frac{1}{4}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 4 is a multiple of 2, so rewrite \(\frac{1}{2}\) with a denominator of 4.
Rewrite as
=
–
=
–
= \(\frac{1}{4}\)
\(\frac{1}{2}\) – \(\frac{1}{4}\) = \(\frac{1}{4}\)
Question 2.
\(\frac{7}{9}\) – \(\frac{2}{3}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 9 is a multiple of 3, so rewrite \(\frac{2}{3}\) with a denominator of 9.
Rewrite as
=
–
=
–
=
\(\frac{7}{9}\) – \(\frac{2}{3}\) = \(\frac{1}{9}\)
Question 3.
\(\frac{6}{5}\) – \(\frac{3}{8}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 8 is not a multiple of 5, so rewrite each fraction with a denominator of 5 8 = 40
Rewrite as
=
as
=
–
=
–
=
\(\frac{6}{5}\) – \(\frac{3}{8}\) =
Apply and Grow: Practice
Subtract.
Question 4.
\(\frac{10}{12}\) – \(\frac{3}{4}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 12 is a multiple of 4, so rewrite \(\frac{3}{4}\) with a denominator of 12.
Rewrite as
=
–
=
–
=
\(\frac{10}{12}\) – \(\frac{3}{4}\) = \(\frac{1}{12}\)
Question 5.
\(\frac{1}{3}\) – \(\frac{1}{6}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 6 is a multiple of 3, so rewrite \(\frac{1}{3}\) with a denominator of 6.
Rewrite as
=
–
=
–
=
\(\frac{1}{3}\) – \(\frac{1}{6}\) = \(\frac{1}{6}\)
Question 6.
\(\frac{9}{10}\) – \(\frac{2}{5}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 10 is a multiple of 5, so rewrite \(\frac{2}{5}\) with a denominator of 10.
Rewrite as
=
–
=
–
= or
\(\frac{9}{10}\) – \(\frac{2}{5}\) = \(\frac{1}{2}\)
Question 7.
\(\frac{5}{4}\) – \(\frac{2}{5}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 5 is not a multiple of 4, so rewrite each fraction with a denominator of 4 5 = 20
Rewrite as
=
as
=
–
=
–
=
\(\frac{5}{4}\) – \(\frac{2}{5}\) = \(\frac{17}{20}\)
Question 8.
\(\frac{13}{16}\) – \(\frac{3}{16}\) – \(\frac{5}{8}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 16 is a multiple of 8, so rewrite \(\frac{5}{8}\) with a denominator of 16.
Rewrite as
=
–
–
= 0
\(\frac{13}{16}\) – \(\frac{3}{16}\) – \(\frac{5}{8}\) = 0
Question 9.
\(\frac{8}{9}\) – (\(\frac{2}{3}\) + \(\frac{1}{6}\)) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator.
common denominator for 9, 3 and 6 = 18
Rewrite as
=
=
–
+
=
–
+
=
\(\frac{8}{9}\) – (\(\frac{2}{3}\) + \(\frac{1}{6}\)) = \(\frac{1}{18}\)
Question 10.
You have \(\frac{1}{3}\) yard of wire. You use \(\frac{1}{3}\) yard to make an electric circuit. How much wire do you have left?

Answer: Left with 0 wire
–
= 0
Question 11.
Your friend finds \(\frac{5}{8}\) – \(\frac{2}{5}\). Explain why his answer is unreasonable. What did he do wrong?
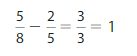
Answer: For subtracting two fractions, the denominators must be same. Here, denominators are different.
So, the answer is wrong
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 8 is not a multiple of 5, so rewrite each fraction with a denominator of 8 5 = 40
Rewrite as
=
as
=
–
=
–
=
\(\frac{5}{8}\) – \(\frac{2}{5}\) = \(\frac{9}{40}\)
Question 12.
Number Sense
Which two fractions have a difference of \(\frac{1}{8}\) ?

Answer:
and
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 8 is a multiple of 2, so rewrite with a denominator of 8.
Rewrite as
=
–
=
–
=
So, fractions and
have the difference of
.
Think and Grow: Modeling Real Life
Example
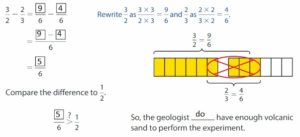
A geologist needs \(\frac{1}{2}\) cup of volcanic sand to perform an experiment. She has \(\frac{3}{2}\) cups of quartz sand. She has \(\frac{2}{3}\) cup more quartz sand than volcanic sand. Can she perform the experiment?

Find how many cups of volcanic sand the geologist has by subtracting \(\frac{2}{3}\) from \(\frac{3}{2}\).
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 3 is not a multiple of 2, so rewrite each fraction with a denominator 2 × 3 = 6.

Answer:
Show and Grow
Question 13.
The world record for the longest dog tail is \(\frac{77}{100}\) meter. The previous record was \(\frac{1}{20}\) meter. shorter than the current record. Was the previous record longer than \(\frac{3}{4}\) meter?

Answer:
Given that,
World record for the longest dog tail is meter.
Previous record was meter shorter than the current record
So subtract meter from the current record to find previous record.
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Rewrite as
Previous record = –
=
=
meter
So the previous record is not longer than meter.
Question 14.
DIG DEEPER!
A woodworker has 1 gallon of paint for a tree house. He uses \(\frac{3}{8}\) gallon to paint the walls and \(\frac{1}{5}\) gallon to paint the ladder. He needs \(\frac{1}{4}\) gallon to paint the roof. Does he have enough paint? Explain.
Answer:
Given that,
Woodworker has 1 gallon of paint
gallon is used to paint the walls.
gallon is used to paint the ladder.
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
=
=
1 – –
=
Therefore, he has more than gallon to paint the roof.
Subtract Fractions with Unlike Denominators Homework & Practice 8.5
Subtract
Question 1.
\(\frac{3}{4}\) – \(\frac{1}{8}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 8 is a multiple of 4, so rewrite \(\frac{3}{4}\) with a denominator of 8
Rewrite as
=
–
=
–
=
\(\frac{3}{4}\) – \(\frac{1}{8}\) =
Question 2.
\(\frac{4}{5}\) – \(\frac{6}{15}\) = __
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 15 is a multiple of 5, so rewrite \(\frac{4}{5}\) with a denominator of 15
Rewrite as
=
–
=
–
=
\(\frac{4}{5}\) – \(\frac{6}{15}\) =
Question 3.
\(\frac{1}{2}\) – \(\frac{1}{8}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 8 is a multiple of 2, so rewrite \(\frac{1}{2}\) with a denominator of 8
Rewrite as
=
–
=
–
=
\(\frac{1}{2}\) – \(\frac{1}{8}\) =
Question 4.
\(\frac{5}{3}\) – \(\frac{3}{4}\) = _____
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 4 is not a multiple of 3, so rewrite each fraction with a denominator of 4 x 3 =12
Rewrite as
=
as
=
–
=
–
=
\(\frac{5}{3}\) – \(\frac{3}{4}\) =
Question 5.
\(\frac{6}{8}\) – \(\frac{7}{10}\) = _____
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 10 is not a multiple of 8, so rewrite each fraction with a denominator of 10 x 8 =80
Rewrite as
=
as
=
–
=
–
=
\(\frac{6}{8}\) – \(\frac{7}{10}\) = =
Question 6.
\(\frac{5}{6}\) – \(\frac{1}{4}\) – \(\frac{3}{12}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 12 is a multiple of 4 and 6, so rewrite each fraction with a denominator of 12
Rewrite as
=
as
=
–
–
=
–
–
=
\(\frac{5}{6}\) – \(\frac{1}{4}\) – \(\frac{3}{12}\) =
Question 7.
You eat \(\frac{1}{12}\) of a vegetable casserole. Your friend eats \(\frac{1}{6}\) of the same casserole. How much more does your friend eat than you?

Answer:
–
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 12 is a multiple of 6, so rewrite with a denominator of 12
Rewrite as
=
–
=
–
=
So, my friend eats of a vegetable casserole than me.
Question 8.
Writing
Why do fractions need a common denominator before you can add or subtract them?
Answer:
In order to add fractions, the fractions must have a common denominator. We need the pieces of each fraction to be the same size to combine them together. These two fractions have the same denominator, so the equal parts that the whole has been split into are the same size.
Question 9.
Logic
Find a.
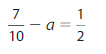
Answer:
a = –
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 10 is a multiple of 2, so rewrite with a denominator of 10
Rewrite as
=
a = –
=
–
a = =
Question 10.
DIG DEEPER!
Write and solve an equation to find the difference between Length A and Length B on the ruler.
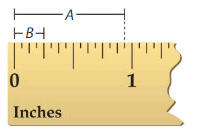
Answer:
\(\frac{1}{10}\) × \(\frac{2}{2}\) = \(\frac{2}{20}\)
\(\frac{9}{10}\) × \(\frac{2}{2}\) = \(\frac{18}{20}\)
\(\frac{18}{20}\) – \(\frac{2}{20}\) = \(\frac{16}{20}\)
Question 11.
Modeling Real Life
You want to stack cups in \(\frac{1}{4}\) minute. Your first attempt takes \(\frac{1}{2}\) minute. Your second attempt takes \(\frac{3}{10}\) minute less than your first attempt. Do you meet your goal?
Answer:
–
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 10 is a multiple of 2, so rewrite with a denominator of 10
Rewrite as
=
–
=
–
=
=
So my second attempt takes minute and I did not meet my goal.
Question 12.
Modeling Real Life
You and your friend each have a canvas of the same size. You divide your canvas into 5 sections and paint 3 of them. Your friend divides her canvas into 7 sections and paints 4 of them. Who paints more? How much more?
Answer:
My canvas =
My friend canvas =
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 7 is a multiple of 5, so rewrite both with a denominator of 7 x 5 = 35
Rewrite as
=
as
=
–
=
–
=
I paint more canvas than my friend.
Review & Refresh
Evaluate. Check whether your answer is reasonable.
Question 13.
1.7 + 5 + 4.3 = ___
Answer: 11
Question 14.
15.24 + 6.13 – 7 = ___
Answer: 14.37
Lesson 8.6 Add Mixed Numbers
Explore and Grow
Use a model to find the sum.
Construct Arguments
How can you add mixed numbers with unlike denominators without using a model? Explain why your method makes sense.
Think and Grow: Add Mixed Numbers
Key Idea
A proper fraction is a fraction less than 1. An improper fraction is a fraction greater than 1. A mixed number represents the sum of a whole number and a proper fraction. You can use equivalent fractions to add mixed numbers.
Example
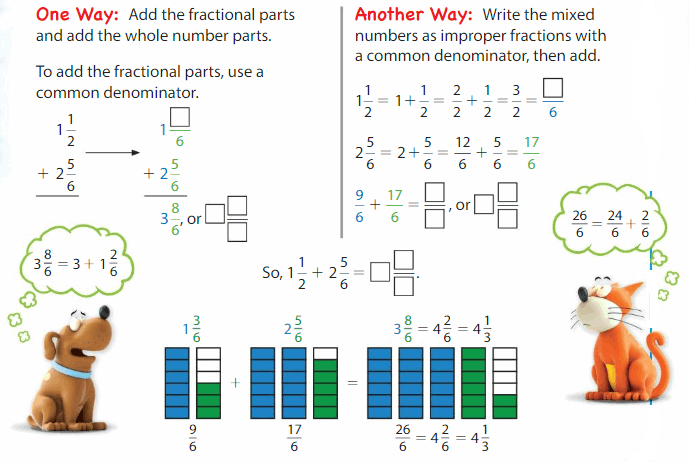
Find 1\(\frac{1}{2}\) + 2\(\frac{5}{6}\)
Show and Grow
Add.
Question 1.
2\(\frac{2}{3}\) + 2\(\frac{1}{6}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
2 = 2
2 = 2
2 + 2
= 4
Question 2.
1\(\frac{5}{12}\) + 3\(\frac{3}{4}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
1 = 1
3 = 3
1 + 3
= 4
= 4
Apply and Grow: Practice
Add.
Question 3.
5\(\frac{4}{9}\) + 1\(\frac{2}{3}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
5 = 5
1 = 1
5 + 1
= 6
=
= 7
Question 4.
3\(\frac{1}{2}\) + \(\frac{5}{12}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
3 = 3
3 +
= 3
+
= 3
Question 5.
4\(\frac{5}{6}\) + 3\(\frac{5}{12}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
4 = 4
3 = 3
4 + 3
= 7
=
= 8
Question 6.
\(\frac{4}{5}\) + 8\(\frac{7}{20}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
Rewrite as
+ 8
=
+ 8
= 8
Question 7.
2\(\frac{1}{3}\) + \(\frac{1}{6}\) + 3\(\frac{2}{3}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
2 = 2
3 = 3
2 +
+ 3
= 2
+
+ 3
= 5
Question 8.
5\(\frac{1}{2}\) + 4\(\frac{3}{4}\) + 6\(\frac{5}{8}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
5 = 5
4 = 4
5 + 4
+ 6
= 5
+ 4
+ 6
= 15
Question 9.
Your science class makes magic milk using 1\(\frac{1}{8}\) cups of watercolor paint and 1\(\frac{3}{4}\) cups of milk. How many cups of magic milk does your class make?

Answer:
Given data,
Watercolor paint = 1 cups
Milk = 1 cups
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
1 = 1
1 + 1
= 2
=
So the class makes 2 cups of magic milk
Question 10.
Structure
Find 2\(\frac{3}{10}\) + 4\(\frac{2}{5}\) two different ways.
Answer:
Method 1:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
4 = 4
2 + 4
= 2
+ 4
= 6
Method 2:
Write the mixed numbers as improper fractions with a common denominator and then add.
2 = 2 +
=
+
=
4 = 4 +
=
=
2 + 4
=
+
=
= 6
Question 11.
DIG DEEPER!
Find the missing numbers.

Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
Rewrite 2 as 2
we can write 4 as
= 3
2 + 1
= 3
= 4
So the missing numbers are 1 and 5.
2 + 1
= 4
Think and Grow: Modeling Real Life
Example
You kayak 1\(\frac{8}{10}\) miles and then take a break. You kayak 1\(\frac{1}{4}\) more miles. How many miles do you kayak altogether?

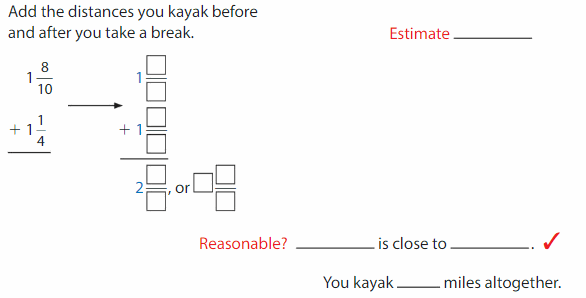
Answer:
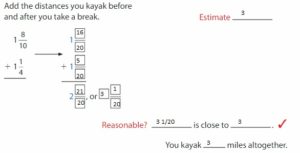
Show and Grow
Question 12.
You listen to a song that is 2\(\frac{3}{4}\) minutes long. Then you listen to a song that is 3\(\frac{1}{3}\) minutes long. How many minutes do you spend listening to the two songs altogether?
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator 4 x 3 = 12.
2 = 2
3 = 3
2 + 3
= 2
+ 3
= 5 min
So I spend 5 min listening to the two songs altogether.
Question 13.
DIG DEEPER!
A beekeeper collects 3\(\frac{3}{4}\) more pounds of honey from Hive 3 than Hive 1. Which hive produces the most honey? Explain.

Answer:
From the given information,
Honey from Hive 3 = Hive 1 honey + 3
= 23 + 3
= 23 + 3
= 26
Use a common denominator for all the hives
Hive 1 honey = 23
Hive 2 honey = 27 = 27
Hive 3 honey = 26
Therefore, Hive 2 produces the most honey.
Add Mixed Numbers Homework & Practice 8.6
Add
Question 1.
6\(\frac{2}{5}\) + 1\(\frac{3}{10}\)
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
6 = 6
6 + 1
= 6
+ 1
= 7
Question 2.
2\(\frac{2}{3}\) + 5\(\frac{3}{6}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator.
2 = 2
2 + 5
= 2
+ 5
= 7
Question 3.
\(\frac{1}{4}\) + 3\(\frac{2}{5}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator 4 x 5 = 20
=
3 = 3
+ 3
=
+ 3
= 3
Question 4.
9\(\frac{5}{7}\) + \(\frac{2}{3}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator 7 x 3 = 21
9 = 9
=
9 +
= 9
+
= 9
Question 5.
2\(\frac{1}{2}\) + 1\(\frac{3}{4}\) + \(\frac{1}{2}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator
2 = 2
1 = 1
=
2 + 1
+
= 2
+1
+
= 3
Question 6.
2\(\frac{2}{3}\) + 4\(\frac{1}{2}\) + 3\(\frac{5}{6}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator
2 = 2
4 = 4
2 + 4
+ 3
= 2
+ 4
+ 3
= 9
2 + 4
+ 3
= 11
Question 7.
A veterinarian spends 3\(\frac{3}{4}\) hours helping cats and 5\(\frac{1}{2}\) hours helping dogs. How many hours does she spend helping cats and dogs altogether?

Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator
3
5 = 5
3 + 5
= 3
+ 5
= 8
So veterinarian spends 8 hours helping cats and dogs altogether.
Question 8.
Writing
How is adding mixed numbers with unlike denominators similar to adding fractions with unlike denominators? How is it different?
Answer:
For both adding mixed numbers and adding fractions we have to use a common denominator.
How it is different?
For adding fractions, directly add the fractions with common denominator.
But for adding mixed numbers, add the fractional parts and add the whole number parts.
Question 9.
Logic
Can you add two mixed numbers and get a sum of 2? Explain.
Answer:
Yes, the sum of two mixed numbers can be equal to 2 but only of one of the mixed numbers is negative.
Question 10.
Structure
Shade the model to represent the sum. Then write an equation to represent your model.

Answer: 4 \(\frac{1}{4}\)
Question 11.
Modeling Real Life
An emperor tamarin has a body length of 9\(\frac{5}{10}\) inches and a tail length of 14\(\frac{1}{4}\) inches. How long is the emperor tamarin?

Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator 10 x 4 = 40
9 = 9
14 = 14
9 + 14
= 9
+ 14
= 23
So, an emperor tamarin is 23 inches long.
Question 12.
DIG DEEPER!
A long jumper jumps 1\(\frac{2}{3}\) feet farther on her third attempt than her second attempt. On which attempt does she jump the farthest? Explain.
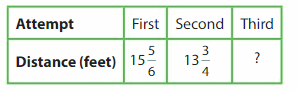
Answer:
Third attempt = 1 + 13
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator 3 x 4 = 12
1 = 1
13 = 13
1 + 13
= 1
+ 13
= 14
Therefore, she jumps the farthest on her first attempt.
Review & Refresh
Find the product. Check whether your answer is reasonable.
Question 13.
354 × 781
Answer:
The number close to 354 is 350
The number close to 781 is 800.
350 × 800 = 280000
354 × 781 = 276474
Yes, the answer is reasonable.
Question 14.
4,029 × 276
Answer:
The number close to 4029 is 4000
The number close to 276 is 300
4000 × 300 = 1200000
4029 × 276 = 1112004
Yes, the answer is reasonable.
Question 15.
950 × 326
Answer:
The number close to 950 is 1000
The number close to 326 is 300
1000 × 300 = 300000
950 × 326 = 309700
Yes, the answer is reasonable.
Lesson 8.7 Subtract Mixed Numbers
Explore and Grow
Use a model to find the difference
3\(\frac{5}{6}\) – 2\(\frac{1}{3}\)
Construct Arguments
How can you subtract mixed numbers with unlike denominators without using a model? Explain why your method makes sense.
Think and Grow: Subtract Mixed Numbers
You can use equivalent fractions to subtract mixed numbers that have fractional parts with unlike denominators.
Example
Find 3\(\frac{1}{4}\) – 1\(\frac{1}{2}\).
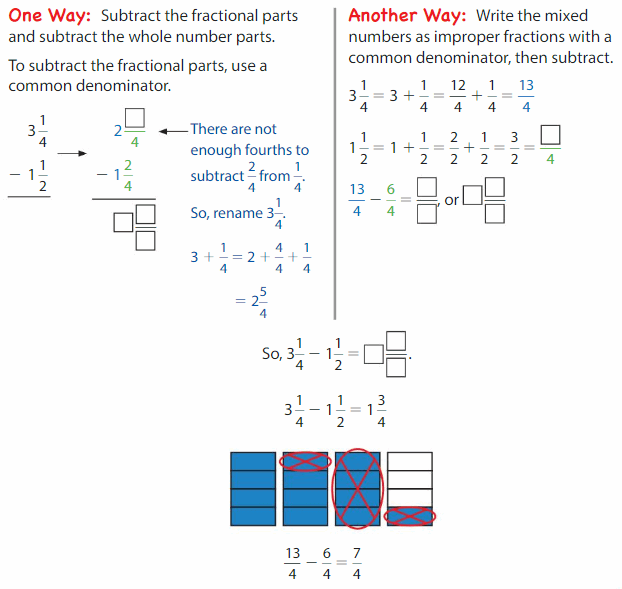
Show and Grow
Subtract.
Question 1.
1\(\frac{4}{5}\) – 1\(\frac{3}{10}\)
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
1 = 1
1 – 1
= 1
– 1
= 0 +
=
Question 2.
5\(\frac{7}{12}\) – 3\(\frac{5}{6}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
3 = 3
5 – 3
= 5
– 3
5 = 4 +
+
= 4
5 – 3
= 4
– 3
= 1
Apply and Grow: Practice
Subtract.
Question 3.
8\(\frac{11}{12}\) – 5\(\frac{2}{3}\) = _____
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
5 = 5
8 – 5
= 8
– 5
8\(\frac{11}{12}\) – 5\(\frac{2}{3}\) = 3 = 3
Question 4.
6 – 4\(\frac{3}{4}\) = ___
Answer:
6 – 4 = 6 –
=
Question 5.
21\(\frac{2}{9}\) – 10\(\frac{1}{3}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
10 = 10
21 = 20 +
+
= 20
21 – 10
= 20
– 10
= 10
Question 6.
7\(\frac{1}{2}\) – \(\frac{5}{8}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
7 = 7
= 6 +
+
= 6
7 –
= 6
–
= 6
Question 7.
9\(\frac{7}{20}\) – 1\(\frac{3}{5}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
1 = 1
9 = 8 +
+
= 8
9 – 1
= 8
– 1
= 7
= 7
Question 8.
7\(\frac{5}{6}\) – 1\(\frac{1}{6}\) – 2\(\frac{2}{3}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
2 = 2
7 = 6 +
+
= 6
7 – 1
– 2
= 6
– 1
– 2
= 3
= 3 + 1
7\(\frac{5}{6}\) – 1\(\frac{1}{6}\) – 2\(\frac{2}{3}\) = 4
Question 9.
A volunteer at a food bank buys 3\(\frac{3}{4}\) pounds of cheese to make sandwiches. She uses 2\(\frac{7}{8}\) pounds. How much cheese does she have left?

Answer:
Given that,
A volunteer buys 3 pounds of cheese
She uses 2 pounds
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
3 = 3
= 2 +
+
= 2
Cheese left = 2 – 2
= 0 +
So she left with pounds of cheese.
Question 10.
Writing
How is adding mixed numbers the same as subtracting mixed numbers? How is it different?
Answer:
Adding and subtracting mixed numbers is same because we need to use a common denominator for both.
Adding and subtracting mixed numbers is different because
For subtracting mixed numbers, the first fraction should be greater than the second number.
Question 11.
Number Sense
Write the words as an expression. Then evaluate.
Subtract the sum of four and three-fourths and two and five-eighths from eleven and seven-eighths.
Answer:
11 – (4
+ 2
)
To subtract or add the fractional parts, use a common denominator.
4 = 4
4 + 2
= 4
+ 2
= 6
11 – (4
+ 2
) = 11
– 6
11 = 10 +
+
= 10
11 – (4
+ 2
) = 10
– 6
11 – (4
+ 2
) = 4
= 4
Question 12.
DIG DEEPER!
Find the missing number.
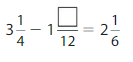
Answer:
To subtract the fractional parts, use a common denominator.
3 = 3
3 – 1
= 3
– 1
= 2
3 – 1
= 2
So the missing number is 1.
Think and Grow: Modeling Real Life
Example
A dragonfly is 1\(\frac{1}{2}\) inches long. How much longer is the walking leaf than the dragonfly?
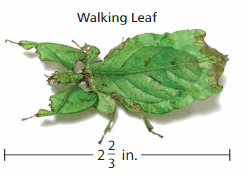
To find how much longer the walking leaf is than the dragonfly, subtract the length of the dragonfly from the length of the walking leaf.

The walking leaf is __ inches longer than the dragonfly.
Answer:
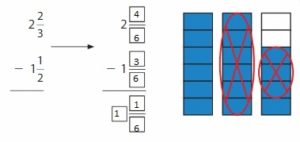
The walking leaf is 1 \(\frac{1}{6}\) inches longer than the dragonfly.
Show and Grow
Question 13.
You volunteer 5\(\frac{3}{4}\) hours in 1 month. You spend 3\(\frac{1}{3}\) hours volunteering at an animal shelter. You spend the remaining hours picking up litter on the side of the road. How many hours do you spend picking up litter?
Answer:
Given that,
Volunteering hours in 1 month = 5
Time spent at an animal shelter = 3
Remaining hours in a month are for picking up litter = 5 – 3
To subtract the fractional parts, use a common denominator 4 x 3 =12
5 = 5
3 = 3
Time spend for picking up litter = 5 – 3
= 2
.
Question 14.
A professional basketball player is 6\(\frac{3}{4}\) feet tall. Your friend is 4\(\frac{5}{6}\) feet tall. How much taller is the basketball player than your friend?
Answer:
To find how much taller is the basketball player than the friend, subtract the height of the friend from the height of the basketball player.
Given that,
Basketball player is 6 feet tall.
My friend is 4 feet tall.
To subtract the fractional parts, use a common denominator 4 x 6 = 24
6 = 6
= 5 +
+
= 5
4 = 4
6 – 4
= 5
– 4
= 1
= 1
The basketball player is 1 feet taller than my friend.
Question 15.
Your rain gauge has 2\(\frac{1}{2}\) inches of water. After a rainstorm, your rain gauge has 1\(\frac{3}{4}\) more inches of water. It is sunny for a week. Now your rain gauge has 2\(\frac{2}{3}\) inches of water. How many inches of water evaporated?
Answer:
After a rainstorm, water in the rain gauge = 2 + 1
To subtract or add the fractional parts, use a common denominator.
2 = 2
Water in the rain gauge = 2 +1
= 2
+ 1
= 3
inches
Water evaporated = 3 – 2
3 = 3
2 = 2
3 – 2
= 3
– 2
= 1
So, 1 inches of water evaporated.
Subtract Mixed Numbers Homework & Practice 8.7
Subtract
Question 1.
9\(\frac{5}{6}\) – 4\(\frac{1}{2}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
4 = 4
9 – 4
= 9
– 4
= 5
9\(\frac{5}{6}\) – 4\(\frac{1}{2}\) = 5 = 5
Question 2.
3\(\frac{2}{3}\) – \(\frac{1}{9}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
3 = 3
3 –
= 3
–
= 3
Question 3.
6\(\frac{1}{3}\) – 1\(\frac{11}{12}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
6 = 6
= 5
6 – 1
= 5
– 1
= 4
Question 4.
12\(\frac{5}{6}\) – 7\(\frac{3}{10}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator 6 x 10 = 60
12 = 12
7 = 7
12 – 7
= 12
– 7
= 5
12\(\frac{5}{6}\) – 7\(\frac{3}{10}\) = 5 = 5
Question 5.
5 – 2\(\frac{3}{4}\) = ___
Answer:
5 – 2 = 5 –
=
Question 6.
4\(\frac{1}{5}\) – 2\(\frac{1}{4}\) = __
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator 5 x 4 = 20
4 = 4
= 3
2 = 2
4 – 2
= 3
– 2
= 1
Subtract.
Question 7.
7\(\frac{5}{8}\) – 1\(\frac{5}{6}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator 8 x 6 = 48
7 = 7
= 6
1 = 1
7 – 1
= 6
– 1
= 5
= 5
Question 8.
8\(\frac{1}{9}\) – 6\(\frac{7}{8}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator 8 x 9 = 72
8 = 8
= 7
6 = 6
8 – 6
= 7
– 6
= 1
Question 9.
1\(\frac{6}{7}\) + 5\(\frac{13}{14}\) – 2\(\frac{1}{2}\) = ___
Answer:
To subtract or add the fractional parts, use a common denominator
1 = 1
2 = 2
1 + 5
– 2
= 1
+ 5
– 2
= 4
= 4
Question 10.
Your friend says the difference of 8 and 3\(\frac{7}{10}\) is 5\(\frac{7}{10}\). Is your friend correct? Explain.
Answer:
8 – 3 = 8 –
=
Question 11.
DIG DEEPER!
Use a symbol card to complete the equation. Then find b.
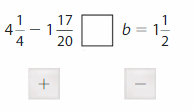
Answer:
4 – 1
– b = 1
4 = 4
= 2
1 = 1
b = 4 – 1
– 1
= 2 – 1
– 1
=
b = =
Question 12.
Modeling Real Life
The world record for the heaviest train pulled with a human beard is 2\(\frac{3}{4}\) metric tons. The world record for the heaviest train pulled by human teeth is 4\(\frac{1}{5}\) metric tons. How much heavier is the train pulled by teeth than the train pulled with a beard?
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator 4 x 5 = 20
2 = 2
4 = 4
= 3
4 – 2
= 3
– 2
= 1
The train pulled by teeth 1 metric tons heavier than the train pulled with a beard.
Question 13.
Modeling Real Life
Your friend’s hair is 50\(\frac{4}{5}\) centimeters long. Your hair is 8\(\frac{9}{10}\) centimeters long. How much longer is your friend’s hair than yours?

Answer:
My friend’s hair = 50 cm
My hair = 8 cm
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator
50 = 50
= 49
50 – 8
= 49
– 8
= 41
My friend’s hair is 41 cms longer than my hair.
Review & Refresh
Question 14.
Round 6.294.
Nearest whole number:
Nearest tenth:
Nearest hundredth:
Answer:
Nearest whole number: 6
Nearest tenth: 60
Nearest hundredth: 600
Question 15.
Round 10.571.
Nearest whole number:
Nearest tenth:
Nearest hundredth:
Answer:
Nearest whole number: 11
Nearest tenth: 110
Nearest hundredth: 1100
Lesson 8.8 Problem Solving: Fractions
Explore and Grow
Make a plan to solve the problem.
At a state park, every \(\frac{1}{10}\) mile of walking trail is marked. Every \(\frac{1}{4}\) mile of a separate biking trail is marked. The table shows the number of mileage markers you and your friend pass while walking and biking on the trails. Who travels farther? How much farther?

Make Sense of Problems
You decide to walk farther and you pass 4 more mileage markers on the walking trail. Does this change your plan to solve the problem? Explain.
Answer:
At a state park, every \(\frac{1}{10}\) mile of the walking trail is marked.
8 × \(\frac{1}{10}\) = \(\frac{8}{10}\)
Every \(\frac{1}{4}\) mile of a separate biking trail is marked.
9 × \(\frac{1}{4}\) = 2 \(\frac{1}{4}\)
\(\frac{8}{10}\) + \(\frac{4}{10}\) = \(\frac{12}{10}\)
= 1 \(\frac{2}{10}\)
Your friend travels more farther.
Think and Gow: Problem Solving: Fractions
Example
To repair a skate ramp, you cut a piece of wood from a 9\(\frac{1}{2}\)-foot-long board. Then you cut the remaining piece in half. Each half is 3\(\frac{5}{12}\) feet long. How long is the first piece you cut?

Understand the Problem
What do you know?
- The board is 9 feet long.2first piece you cut.
- You cut a piece from the board.
- You cut the rest into two pieces that are each 3\(\frac{5}{12}\) feet long.
What do you need tofind?
- You need to find the length of the first piece you cut.
Make a Plan
How will you solve?
Write and solve an equation: Subtract the sum of the lengths of the last two pieces you cut from the total length of the board.
Solve
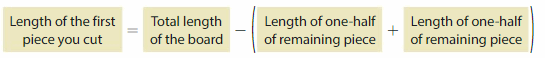
Let g represent the length of the first piece you cut.
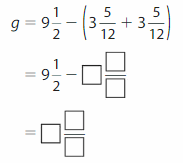
So, the length of the first piece you cut is __ feet.
Answer:
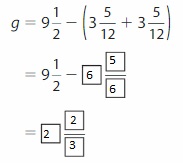
So, the length of the first piece you cut is 2 \(\frac{2}{3}\) feet.
Show and Grow
Question 1.
Explain how you can check your answer in the example above.
Answer:
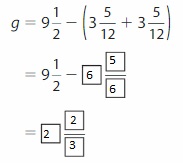
Apply and Grow: Practice
Understand the problem. What do you know? What do you need to find? Explain.
Question 2.
A racehorse eats 38\(\frac{1}{2}\) pounds of food each day. He eats 22\(\frac{3}{4}\) pounds of hay and 7\(\frac{1}{2}\) pounds of grains. How many pounds of his daily diet is not hay or grains?

Answer:
Given,
A racehorse eats 38\(\frac{1}{2}\) pounds of food each day.
He eats 22\(\frac{3}{4}\) pounds of hay and 7\(\frac{1}{2}\) pounds of grains.
38\(\frac{1}{2}\) – 22\(\frac{3}{4}\)
= 15 \(\frac{3}{4}\)
Thus 15 \(\frac{3}{4}\) pounds of his daily diet is not grains.
Question 3.
In 2015, American Pharoah won all of the horse races shown in the table. How many kilometers did American Pharoah run in the races altogether?
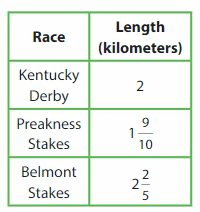
Understand the problem. Then make a plan. How will you solve? Explain.
Answer:
Add all the lengths to find how many kilometers did American Pharoah run in the races altogether.
2 + 1 \(\frac{9}{10}\) + 2 \(\frac{2}{5}\)
First add all the whole numbers.
2 + 1 + 2 = 5
Now add the fractions
\(\frac{9}{10}\) + \(\frac{4}{10}\) = 1 \(\frac{3}{10}\)
5 + 1 \(\frac{3}{10}\) = 6 \(\frac{3}{10}\)
Question 4.
You have 2\(\frac{1}{2}\) cups of blueberries. You use 1\(\frac{1}{4}\) cups for pancakes and \(\frac{1}{2}\) cup for muffins. What fraction of a cup of blueberries do you have left?
Answer:
Given,
You have 2\(\frac{1}{2}\) cups of blueberries.
You use 1\(\frac{1}{4}\) cups for pancakes and \(\frac{1}{2}\) cup for muffins.
1\(\frac{1}{4}\) + \(\frac{1}{2}\) = 1 \(\frac{3}{4}\)
2\(\frac{1}{2}\) – 1 \(\frac{3}{4}\) = \(\frac{3}{4}\)
Question 5.
A customer orders 2 pounds of cheese at a deli. The deli worker places some cheese in a bowl and weighs it. The scale shows 1\(\frac{1}{4}\) pounds. The bowl weighs \(\frac{1}{8}\) pound. What fraction of a pound of cheese does the worker need to add to the bowl?
Answer:
Given,
A customer orders 2 pounds of cheese at a deli. The deli worker places some cheese in a bowl and weighs it.
The scale shows 1\(\frac{1}{4}\) pounds. The bowl weighs \(\frac{1}{8}\) pound.
1\(\frac{1}{4}\) + \(\frac{1}{8}\) = 1 \(\frac{3}{8}\)
2 – 1 \(\frac{3}{8}\) = \(\frac{5}{8}\)
Question 6.
Reasoning
Student A is 8\(\frac{1}{2}\) inches shorter than Student B. Student B is 3\(\frac{1}{4}\) inches taller than Student C. Student C is 56\(\frac{3}{8}\) inches tall. How tall is Student A? Student B?
Answer:
Student A is 8\(\frac{1}{2}\) inches shorter than Student B.
Student B is 3\(\frac{1}{4}\) inches taller than Student C.
Student C is 56\(\frac{3}{8}\) inches tall.
Student B is 56\(\frac{3}{8}\) + 3\(\frac{1}{4}\) = 59 \(\frac{5}{8}\)
Thus the height of student B is 59 \(\frac{5}{8}\) inches.
Student A is 59 \(\frac{5}{8}\) – 8\(\frac{1}{2}\) = 51 \(\frac{1}{8}\)
Thus the height of Student A is 51 \(\frac{1}{8}\) inches.
Question 7.
DIG DEEPER!
A police dog spends \(\frac{1}{8}\) of his workday in a police car, \(\frac{3}{4}\) of his workday in public, and the rest of his workday at the police station. What fraction of the dog’s day is spent at the police station?
Answer:
Given,
A police dog spends \(\frac{1}{8}\) of his workday in a police car, \(\frac{3}{4}\) of his workday in public, and the rest of his workday at the police station.
\(\frac{1}{8}\) + \(\frac{3}{4}\) = \(\frac{7}{8}\)
1 – \(\frac{7}{8}\) = \(\frac{1}{8}\)
Thus \(\frac{1}{8}\) fraction of the dog’s day is spent at the police station
Think and Grow: Modeling Real Life
Example
The Magellan spacecraft, launched by the United States, spent 5\(\frac{5}{12}\) years in space before it burned in Venus’s atmosphere. Its first 4 cycles around Venus each lasted \(\frac{2}{3}\) year. The remaining cycles around Venus lasted a total of 1\(\frac{1}{2}\) years. How long did it take to travel from Earth to Venus?

Think: What do you know? What do you need to find? How will you solve?
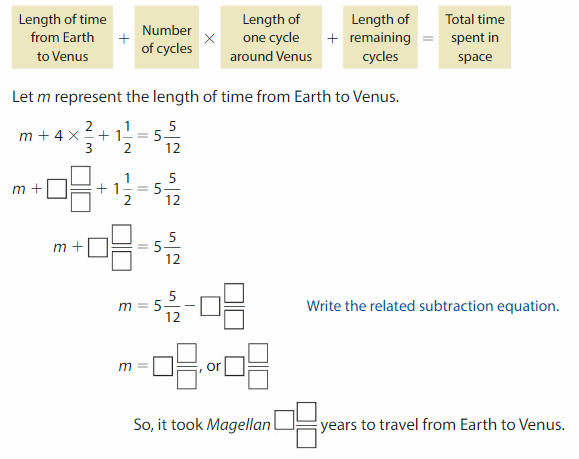
Answer:
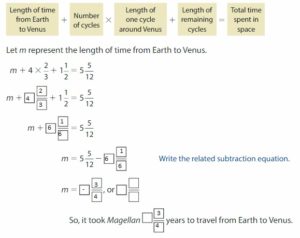
Show and Grow
Question 8.
You have one of each euro coin shown. Your friend has four euro coins that have a total weight of 21\(\frac{3}{10}\) grams. Whose coins weigh more? How much more?
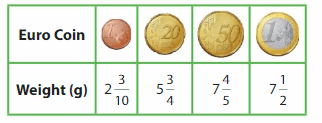
Answer:
2 \(\frac{3}{10}\) + 5 \(\frac{3}{4}\) + 7 \(\frac{4}{5}\) + 7 \(\frac{1}{2}\)
= 23 \(\frac{7}{20}\)
23 \(\frac{7}{20}\) – 21\(\frac{3}{10}\)
= 2 \(\frac{1}{20}\)
Problem Solving: Fractions Homework & Practice 8.8
Understand the problem. What do you know? What do you need to find? Explain.
Question 1.
Your goal is to exercise for 15 hours this month. You exercise for 3\(\frac{1}{2}\) hours the first week and 3\(\frac{3}{4}\) hours the next week. How many more hours do you need to exercise to reach your goal?
Answer:
Given,
Your goal is to exercise for 15 hours this month.
You exercise for 3\(\frac{1}{2}\) hours the first week and 3\(\frac{3}{4}\) hours the next week.
3\(\frac{1}{2}\) + 3\(\frac{3}{4}\) = 7 \(\frac{1}{4}\)
15 – 7 \(\frac{1}{4}\) = 7 \(\frac{3}{4}\) hours
Question 2.
A taxi driver travels 4\(\frac{5}{8}\) miles to his first stop. He travels 1\(\frac{3}{4}\) miles less to his second stop. How many miles does the taxi driver travel for the two stops?

Understand the problem. Then make a plan. How will you solve? Explain.
Answer:
Given,
A taxi driver travels 4\(\frac{5}{8}\) miles to his first stop. He travels 1\(\frac{3}{4}\) miles less to his second stop.
4\(\frac{5}{8}\) + 1\(\frac{3}{4}\) = 7 \(\frac{1}{4}\)
Question 3.
During the U.S. Civil War, \(\frac{5}{9}\) of the states fought for the Union, and \(\frac{11}{36}\) of the states fought for the Confederacy. The rest of the states were border states. What fraction of the states were border states?
Answer:
Given,
During the U.S. Civil War, \(\frac{5}{9}\) of the states fought for the Union, and \(\frac{11}{36}\) of the states fought for the Confederacy. The rest of the states were border states.
\(\frac{5}{9}\) + \(\frac{11}{36}\) = \(\frac{31}{36}\)
Question 4.
You have 6\(\frac{3}{4}\) pounds of clay. You use 4\(\frac{1}{6}\) pounds to make a medium-sized bowl and 1\(\frac{1}{2}\) pounds to make a small bowl. How many pounds of clay do you have left?
Answer:
Given,
You have 6\(\frac{3}{4}\) pounds of clay.
You use 4\(\frac{1}{6}\) pounds to make a medium-sized bowl and 1\(\frac{1}{2}\) pounds to make a small bowl.
4\(\frac{1}{6}\) + 1\(\frac{1}{2}\) = 5 \(\frac{2}{3}\)
6\(\frac{3}{4}\) – 5 \(\frac{2}{3}\) = 1 \(\frac{1}{12}\)
Question 5.
DIG DEEPER!
Newton and Descartes have a 70-day summer vacation. They go to camp for \(\frac{23}{70}\) of their vacation, and they travel for \(\frac{6}{35}\) of their vacation. They stay home the rest of their vacation. How many weeks do Newton and Descartes spend at home?
Answer:
Given,
Newton and Descartes have a 70-day summer vacation. They go to camp for \(\frac{23}{70}\) of their vacation, and they travel for \(\frac{6}{35}\) of their vacation.
\(\frac{23}{70}\) + \(\frac{6}{35}\) = \(\frac{1}{2}\)
That means Newton and Descartes spend 5 weeks at home.
Question 6.
Modeling Real Life
A farmer plants beets in a square garden with side lengths of 12\(\frac{2}{3}\) feet. He plants squash in a garden with a perimeter of 50\(\frac{1}{2}\) feet. Which garden has a greater perimeter? How much greater is it?
Answer:
Given,
A farmer plants beets in a square garden with side lengths of 12\(\frac{2}{3}\) feet.
The perimeter of the square = 4s
P = 4 × 12\(\frac{2}{3}\)
P = 50 \(\frac{2}{3}\)
50 \(\frac{2}{3}\) is greater than 50\(\frac{1}{2}\)
Question 7.
DIG DEEPER!
Which grade uses more leafy greens daily for its classroom rabbits? How much more does it use?

Answer: 4th Grade uses more leafy greens.
Review & Refresh
Find the product.
Question 1.
0.43 × 1,000 = 430
Answer:
43 x 10-2 x 103 = 43 x 101
= 430
Question 2.
25.8 × 0.1 = 2.58
Answer:
258 x 10-1 x 10-1= 2.58
Add and Subtract Fractions Performance Task 8
Many historic landmarks are located in Washington, D.C.
Question 1.
Initial construction of the Washington Monument began in 1848. When the height of the monument reached 152 feet, construction halted due to lack of funds. How many feet were added to the height of the monument when construction resumed 23 years later?

Answer:
The initial construction of the Washington Monument began in 1848. When the height of the monument reached 152 feet, construction halted due to lack of funds.
554 \(\frac{3}{4}\) – 152 = 402 \(\frac{3}{4}\)
Question 2.
You visit several historic landmarks. You start at the Capitol Building and walk to the Washington Monument, then the Lincoln Memorial, then the White House, and then back to the Capitol Building.
a. You walk 3 miles each hour. It takes you \(\frac{1}{2}\) hour to walk from the Lincoln Memorial to the White House. What is the distance from the Lincoln Memorial to the White House? Label the map.
Answer:
b. What is the total distance you walk visiting the landmarks?
Answer: 1 \(\frac{1}{5}\) + \(\frac{4}{5}\) + 1 \(\frac{4}{5}\) + 1 \(\frac{3}{5}\)
= 5 \(\frac{2}{5}\)
Question 3.
A law in Washington, D.C., restricts a new building’s height to no more than 20 feet taller than the width of the street it faces. You design a building with stories that are each 15 feet tall for a street that is 88\(\frac{2}{3}\) feet wide. What is the greatest number of stories your building can have? How much shorter is your building than the height restriction?
Answer:
Given,
A law in Washington, D.C., restricts a new building’s height to no more than 20 feet taller than the width of the street it faces.
20 × 88\(\frac{2}{3}\) = 1773 \(\frac{1}{3}\)
You design a building with stories that are each 15 feet tall for a street that is 88\(\frac{2}{3}\) feet wide.
15 × 88\(\frac{2}{3}\) = 1330
1773 \(\frac{1}{3}\) – 1330 = 443 \(\frac{1}{3}[/latex
Add and Subtract Fractions Activity
Mixed Number Number
Subtract and Add
Directions:
- Each player flips four Mixed Number Cards.
- Each player arranges the cards to create two differences that will have the greatest possible sum.
- Each player records the two differences, and then adds the differences.
- Players repeat Steps 1–3.
- Each player adds Sum A and Sum B to find the total. The player with the greatest total wins!
Answer:
Add and Subtract Fractions Performance Chapter Practice
8.1 Simplest Form
Write the fraction in simplest form.
Question 1.
[latex]\frac{2}{12}\)
Answer:
Step 1: Find the common factors of 2 and 12.
Factors of 2: 1, 2
Factors of 12: 1, 2, 3, 4, 6, 12
The common factors of 2 and 12 are 1 and 2.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 6 have no common factors other than 1, \(\frac{2}{12}\) is in simplest form.
Question 2.
\(\frac{15}{30}\)
Answer:
Step 1: Find the common factors of 15 and 30.
Factors of 15: 1, 3, 5, 15
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
The common factors of 15 and 30 are 1, 3, 5 and 15.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 2 have no common factors other than 1, \(\frac{15}{30}\) is in simplest form.
Question 3.
\(\frac{16}{24}\)
Answer:
Step 1: Find the common factors of 16 and 24.
Factors of 16: 1, 2, 4, 8, 16
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
The common factors of 16 and 24 are 1, 2, 4 and 8.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 2 and 3 have no common factors other than 1, \(\frac{16}{24}\) is in simplest form.
Question 4.
\(\frac{18}{36}\)
Answer:
Step 1: Find the common factors of 18 and 36.
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
The common factors of 18 and 36 are 1, 2, 3, 6, 9 and 18.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 2 have no common factors other than 1, \(\frac{18}{36}\) is in simplest form.
Question 5.
\(\frac{8}{32}\)
Answer:
Step 1: Find the common factors of 8 and 32.
Factors of 8: 1, 2, 4, 8
Factors of 32: 1, 2, 4, 8, 16, 32
The common factors of 8 and 32 are 1, 2, 4 and 8.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 1 and 4 have no common factors other than 1, \(\frac{8}{32}\) is in simplest form.
Question 6.
\(\frac{25}{10}\)
Answer:
Step 1: Find the common factors of 25 and 10.
Factors of 25: 1, 5, 25
Factors of 10: 1, 2, 5, 10
The common factors of 25 and 10 are 1 and 5.
Step 2: Write an equivalent fraction by dividing the numerator and the denominator by the greatest of the common factors.
Because 5 and 2 have no common factors other than 1, \(\frac{25}{10}\) is in simplest form.
8.2 Estimate Sums and Differences of Fractions
Estimate the sum or difference.
Question 7.
\(\frac{7}{8}\) – \(\frac{1}{5}\)
Answer:
Step 1: Use mental math to estimate each fraction.
is about
Think: The numerator is about the same as the denominator.
is about
Think: The numerator is near to zero.
Step 2: Estimate the difference.
An estimate of –
is 1 – 0 = 1.
Question 8.
\(\frac{5}{6}\) + \(\frac{9}{10}\)
Answer:
Step 1: Estimate each fraction.
is between
and 1, but is closer to 1.
is between
and 1, but is closer to 1.
Step 2: Estimate the sum.
An estimate of \(\frac{5}{6}\) + \(\frac{9}{10}\) = 1 + 1 = 2.
Question 9.
\(\frac{11}{12}\) – \(\frac{89}{100}\)
Answer:
Step 1: Use mental math to estimate each fraction.
is about
Think : The numerator is about the same as the denominator.
is about
Think : The numerator is closer to denominator.
Step 2: Estimate the difference.
An estimate of –
is 1 – 1 = 0.
Question 10.
Precision
Your friend says \(\frac{7}{8}\) – \(\frac{5}{12}\) is about 0. Find a closer estimate. Explain why your estimate is closer.
Answer:
\(\frac{7}{8}\) – \(\frac{5}{12}\) = \(\frac{11}{24}\)
\(\frac{11}{24}\) = 0.45
The number 0.45 is close to 0.
8.3 Find Common Denominators
Use a common denominator to write an equivalent fraction for each fraction.
Question 11.
\(\frac{1}{4}\) and \(\frac{1}{2}\)
Answer:
Use the product of the denominators: 4 2 = 8
Write equivalent fractions with denominators of 8
Therefore, equivalent fractions are and
.
Question 12.
\(\frac{2}{3}\) and \(\frac{2}{9}\)
Answer:
Use the product of the denominators : 3 9 = 27
Write equivalent fractions with denominators of 27
Therefore, equivalent fractions are and
.
Question 13.
\(\frac{2}{3}\) and \(\frac{5}{6}\)
Answer:
Use the product of the denominators : 3 6 = 18
Write equivalent fractions with denominators of 18
Therefore, equivalent fractions are and
.
Question 14.
\(\frac{4}{5}\) and \(\frac{1}{3}\)
Answer:
Use the product of the denominators : 5 3 = 15
Write equivalent fractions with denominators of 15
Therefore, equivalent fractions are and
.
Question 15.
\(\frac{5}{6}\) and \(\frac{8}{9}\)
Answer:
Use the product of the denominators : 6 9 = 54
Write equivalent fractions with denominators of 54
Therefore, equivalent fractions are and
.
Question 16.
\(\frac{4}{5}\) and \(\frac{3}{4}\)
Answer:
Use the product of the denominators : 5 4 = 20
Write equivalent fractions with denominators of 20
Therefore, equivalent fractions are and
.
8.4 Add Fractions with Unlike Denominators
Add
Question 17.
\(\frac{2}{15}\) + \(\frac{2}{3}\) = __
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 15 is a multiple of 3, so rewrite \(\frac{2}{3}\) with a denominator of 15.
Rewrite as
=
+
=
+
=
Question 18.
\(\frac{3}{4}\) + \(\frac{1}{8}\) = __
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 8 is a multiple of 4, so rewrite \(\frac{3}{4}\) with a denominator of 8.
Rewrite as
=
+
=
+
=
Question 19.
\(\frac{7}{2}\) + \(\frac{1}{6}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 6 is a multiple of 2, so rewrite \(\frac{7}{2}\) with a denominator of 6.
Rewrite as
=
+
=
+
=
=
Question 20.
\(\frac{5}{9}\) + \(\frac{1}{2}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 9 is not a multiple of 2, so rewrite each fraction with a denominator of 9 x 2 = 18.
Rewrite as
=
as
=
+
=
+
=
Question 21.
\(\frac{7}{10}\) + \(\frac{5}{6}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 10 is not a multiple of 6, so rewrite each fraction with a denominator of 10 x 6 = 60.
Rewrite as
=
as
=
+
=
+
=
Question 22.
\(\frac{1}{6}\) + \(\frac{11}{12}\) + \(\frac{4}{6}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the sum.
Think: 12 is a multiple of 6, so rewrite each fraction with a denominator of 12.
Rewrite as
=
as
=
+
+
=
+
+
=
=
8.5 Subtract Fractions with Unlike Denominators
Subtract
Question 23.
\(\frac{1}{4}\) – \(\frac{1}{8}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 8 is a multiple of 4, so rewrite \(\frac{1}{4}\) with a denominator of 8.
Rewrite as
=
–
=
–
=
Question 24.
\(\frac{3}{2}\) – \(\frac{7}{10}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 10 is a multiple of 2, so rewrite \(\frac{3}{2}\) with a denominator of 10.
Rewrite as
=
–
=
–
=
=
Question 25.
\(\frac{15}{16}\) – \(\frac{7}{8}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 16 is a multiple of 8, so rewrite \(\frac{7}{8}\) with a denominator of 16.
Rewrite as
=
–
=
–
=
Question 26.
\(\frac{4}{3}\) – \(\frac{2}{5}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 5 is not a multiple of 3, so rewrite each fraction with a denominator of 5 x 3 = 15.
Rewrite as
=
as
=
–
=
–
=
Question 27.
\(\frac{5}{6}\) – \(\frac{3}{4}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 6 is not a multiple of 4, so rewrite each fraction with a denominator of 6 x 4 = 24.
Rewrite as
=
as
=
–
=
–
=
=
Question 28.
\(\frac{7}{10}\) – \(\frac{2}{5}\) + \(\frac{11}{20}\) = ___
Answer:
Use equivalent fractions to write the fractions with a common denominator. Then find the difference.
Think: 20 is a multiple of 10 and 5, so rewrite each fraction with a denominator of 20.
Rewrite as
=
as
=
–
+
=
–
+
8.6 Add Mixed Numbers
Add
Question 29.
1\(\frac{3}{4}\) + 7\(\frac{5}{8}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator
1 = 1
1 + 7
= 1
+ 7
= 8
Question 30.
3\(\frac{3}{10}\) + 2\(\frac{7}{20}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator
3 = 3
3 + 2
= 3
+ 2
= 5
Question 31.
\(\frac{1}{3}\) + 6\(\frac{4}{5}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator 3 x 5 = 15
=
6 = 6
+ 6
=
+ 6
= 6
Question 32.
5\(\frac{8}{9}\) + \(\frac{5}{6}\) = _____
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator 9 x 6 = 54
5 = 5
=
5 +
= 5
+
= 5
Question 33.
2\(\frac{2}{3}\) + \(\frac{4}{9}\) + 4\(\frac{1}{3}\) = ___
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator
2 = 2
4 = 4
2 +
+ 4
= 2
+
+ 4
= 6
Question 34.
5\(\frac{1}{2}\) + 2\(\frac{5}{8}\) + 3\(\frac{3}{4}\) = _____
Answer:
Add the fractional parts and add the whole number parts.
To add the fractional parts, use a common denominator
5 = 5
3 = 3
5 + 2
+ 3
=5
+ 2
+ 3
= 10
8.7 Subtract Mixed Numbers
Subtract
Question 35.
8\(\frac{7}{10}\) – 1\(\frac{2}{5}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
1 = 1
8 – 1
= 8
– 1
= 7
Question 36.
15\(\frac{97}{100}\) – 10\(\frac{7}{20}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
10 = 10
15 – 10
= 15
– 10
= 5
Question 37.
4 – 3\(\frac{5}{6}\) = ___
Answer:
4 – 3 = 4 –
=
Question 38.
5\(\frac{1}{3}\) – 2\(\frac{1}{2}\) = _____
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator 3 x 2 = 6.
5 = 5
= 4
2 = 2
5 – 2
= 4
– 2
= 2
Question 39.
9\(\frac{2}{5}\) – 6\(\frac{3}{4}\) = ___
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator 5 x 4 = 20.
9 = 9
= 8
6 = 6
9 – 6
= 8
– 6
= 2
Question 40.
2\(\frac{3}{8}\) + 7\(\frac{1}{2}\) – 1\(\frac{11}{16}\) = ____
Answer:
To add or subtract the fractional parts, use a common denominator.
2 = 2
7 = 7
2 + 7
– 1
= 2
+ 7
– 1
= 8
Question 41.
Modeling Real Life
A family adopts a puppy that weighs 7\(\frac{7}{8}\) pounds. They take him to the vet 2 weeks later, and he weighs 12\(\frac{3}{16}\) pounds. How much weight did the puppy gain?
Answer:
Subtract the fractional parts and subtract the whole number parts.
To subtract the fractional parts, use a common denominator.
7 = 7
12 – 7
= 12
– 7
= 11 – 7
= 4
So the puppy gains 4 pounds weight.
8.8 Problem Solving: Fractions
Question 42.
A radio station plays three commercials between two songs. The commercials play for 2 minutes altogether. The first commercial is \(\frac{1}{2}\) minute, and the second commercial is 1\(\frac{1}{4}\) minutes. How long is the third commercial?
Answer:
Given,
A radio station plays three commercials between two songs.
The commercials play for 2 minutes altogether. The first commercial is \(\frac{1}{2}\) minute, and the second commercial is 1\(\frac{1}{4}\) minutes.
\(\frac{1}{2}\) + 1\(\frac{1}{4}\) = 1 \(\frac{3}{4}\)
2 – 1 \(\frac{3}{4}\) = \(\frac{1}{4}\)
Question 43.
Your friend plants a tree seedling on Earth Day that is 1\(\frac{1}{3}\) feet tall. In 1 year, the tree grows 1\(\frac{5}{6}\) feet. After 2 years, the tree is 4\(\frac{11}{12}\) feet tall. How much did the tree grow in the second year?

Answer:
Given,
Your friend plants a tree seedling on Earth Day that is 1\(\frac{1}{3}\) feet tall.
In 1 year, the tree grows 1\(\frac{5}{6}\) feet. After 2 years, the tree is 4\(\frac{11}{12}\) feet tall.
4\(\frac{11}{12}\) – 1\(\frac{5}{6}\) = 3 \(\frac{1}{12}\)
3 \(\frac{1}{12}\) – 1\(\frac{1}{3}\) = 1 \(\frac{3}{4}\)
Thus the growth of the tree in the second year is 1 \(\frac{3}{4}\) feet.
Conclusion:
Enhance your math skills and performance skills by referring to our Big Ideas Math Grade 5 Answer Key for Chapter 8 Add and Subtract Fractions. Make use of the links to complete your homework and assignments. Practice the given questions number of times to score the highest marks in the exams. Also, keep in touch with our site to get the Solution Key for all Big Ideas Math Grade 5 Chapters from 1 to 14.