Big Ideas Math Geometry Answers Chapter 3 Parallel and Perpendicular Lines

Are you searching for a preparation guide regarding Geometry Concepts? If yes, then try our Big Ideas Math Geometry Answers Chapter 3 Parallel and Perpendicular Lines. Make BIM Book Geometry Chapter 3 Parallel and Perpendicular Lines Solution Key as a reference and clear all your queries on Big Ideas Math Geometry Ch 3 Parallel and Perpendicular Lines Questions. The Questions and Answers you see here are prepared in the Parallel and Perpendicular Lines Big Ideas Math Geometry Ch 3 Answer Key as per the latest common core curriculum.

Big Ideas Math Book Geometry Answer Key Chapter 3 Parallel and Perpendicular Lines

Parallel and Perpendicular Lines are basic concepts in Geometry. Big Ideas Math Book Geometry Answer Key Chapter 3 Parallel & Perpendicular Lines covers questions from Exercises, Chapter Tests, Review Tests, and Cumulative Assessments. So, to make this a better learning experience, we have compiled all the Big Ideas Math Geometry Answers Chapter 3 as per the BIM Geometry Textbook’s latest syllabus. Just click on the links provided below to learn the fundamentals involved in Big Ideas Math Book Geometry Answer Key Chapter 3 Parallel and Perpendicular Lines.

• Parallel and Perpendicular Lines Maintaining Mathematical Proficiency – Page 123 
• Parallel and Perpendicular Lines Mathematical Practices – Page 124
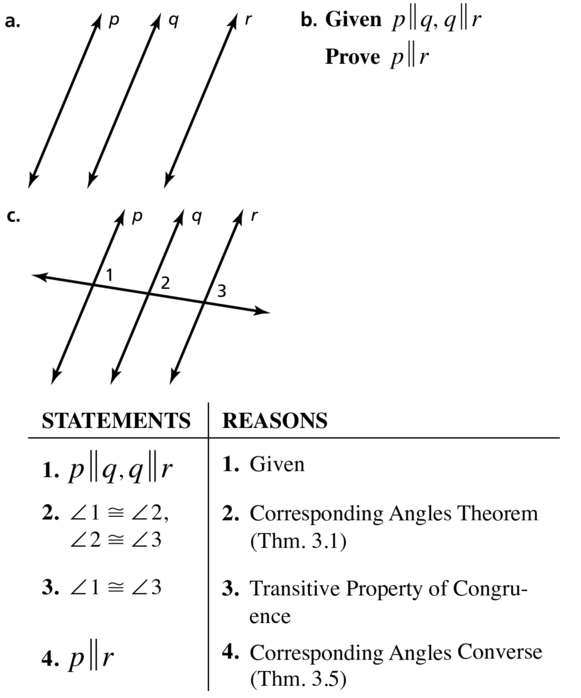
• 3.1 Pairs of Lines and Angles – Page(125-130)
• Lesson 3.1 Pairs of Lines and Angles – Page(126-128)
• Exercise 3.1 Pairs of Lines and Angles – Page(129-130)
• 3.2 Parallel Lines and Transversals – Page(131-136)
• Lesson 3.2 Parallel Lines and Transversals – Page(132-134)
• Exercise 3.2 Parallel Lines and Transversals – Page(135-136)
• 3.3 Proofs with Parallel Lines – Page(137-144)
• Lesson 3.3 Proofs with Parallel Lines – Page(138-141)
• Exercise 3.3 Proofs with Parallel Lines – Page(142-144)
• 3.1 – 3.3 Study Skills: Analyzing Your Errors – Page 145
• 3.1 – 3.3 Quiz – Page 146
• 3.4 Proofs with Perpendicular Lines – Page(147-154)
• Lesson 3.4 Proofs with Perpendicular Lines – Page(148-151)
• Exercise 3.4 Proofs with Perpendicular Lines – Page(152-154)
• 3.5 Equations of Parallel and Perpendicular Lines – Page(155-162)
• Lesson 3.5 Equations of Parallel and Perpendicular Lines – Page(156-159)
• Exercise 3.5 Equations of Parallel and Perpendicular Lines – Page(160-162)
• 3.4 – 3.5 Performance Task: Navajo Rugs – Page 163
• Parallel and Perpendicular Lines Chapter Review – Page(164-166)
• Parallel and Perpendicular Lines Test – Page 167
• Parallel and Perpendicular Lines Cumulative Assessment – Page(168-169)

Parallel and Perpendicular Lines Maintaining Mathematical Proficiency

Find the slope of the line.

Question 1.

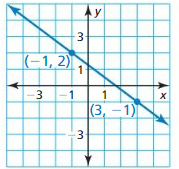
Answer:
The given points are A (-1, 2), and B (3, -1)
Compare the given points with A (x1, y1), B (x2, y2)
m = \(\frac{y2 – y1}{x2 – x1}\)
Substitute A (-1, 2), and B (3, -1) in the formula.
m = \(\frac{-1 – 2}{3 + 1}\) = \(\frac{-3}{4}\)
So, slope of the given line is \(\frac{-3}{4}\)

Question 2.

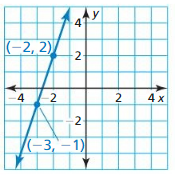
Answer:
The given points are A (-2, 2), and B (-3, -1)
Compare the given points with A (x1, y1), B (x2, y2)
Substitute A (-2, 2), and B (-3, -1) in the formula.
m = \(\frac{y2 – y1}{x2 – x1}\)
m = \(\frac{-1 – 2}{-3 + 2}\)
m = \(\frac{-3}{-1}\)
m = 3
So, the slope of the given line is 3.

Question 3.

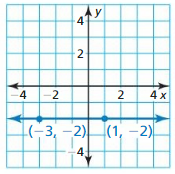
Answer:
The given points are A (-3, -2), and B (1, -2)
Compare the given points with A (x1, y1), B (x2, y2)
m = \(\frac{y2 – y1}{x2 – x1}\)
m = \(\frac{-2 + 2}{3 + 1}\)
m = \(\frac{0}{4}\)
m = 0
So, the slope of the given line is 0.

Write an equation of the line that passes through the given point and has the given slope.

Question 4.
(6, 1); m = – 3
Answer:
Given, (6, 1) and m = -3
The equation of a line y = mx + b
Where,
m is the slope
b is the y-intercept
Substitute the values in the equation.
y = -3x + b
To find the value of b,
1 = -3 (6) + b
1 = -18 + b
1 + 18 = b
b = 19
So, the equation of the line along with the y-intercept is y = -3x + 19

Question 5.
(-3, 8); m = – 2
Answer:
Given (-3, 8) and m = -2
The equation of a line is y = mx + b
Where,
m is the slope
b is the y-intercept
y = -2x + b
Substitute the given point in the equation.
x = -3 and y = 8
8 = -2 (-3) + b
8 = 6 + b
8 – 6 = b
b = 2
So, the equation of the line along with the y-intercept is y = -2x + 2

Question 6.
(- 1, 5); m = 4
Answer:
Given (-1, 5) and m = 4
The equation of a line is y = mx + b
Where,
m is the slope
b is the y-intercept
y = 4x + b
Substitute the given point in the equation
5 = 4 (-1) + b
5 = -4 + b
5 + 4 = b
b = 9
So, the equation of the line along with the y-intercept is y = 4x + 9

Question 7.
(2, – 4); m = \(\frac{1}{2}\)
Answer:
Given (2, -4) and m = \(\frac{1}{2}\)
The equation of a line is y = mx + b
Where,
m is the slope
b is the y-intercept
y = \(\frac{1}{2}\)x + b
Substitute the given point in the equation.
-4 = \(\frac{1}{2}\) (2) + b
-4 = 1 + b
-4 – 1 = b
b = -5
So, the equation of the line along with the y-intercept is y = \(\frac{1}{2}\)x – 5

Question 8.
(- 8, – 5); m = –\(\frac{1}{4}\)
Answer:
Given (-8, -5) and m = –\(\frac{1}{4}\)
The equation of a line is y = mx + b
Where,
m is the slope
b is the y-intercept
y = –\(\frac{1}{4}\)x + b
Substitute the given point in the equation
-5 = –\(\frac{1}{4}\) (-8) + b
-5 = 2 + b
-5 – 2 = b
b = -7
So, the equation of the line along with the y-intercept is y = –\(\frac{1}{4}\)x – 7

Question 9.
(0, 9); m = \(\frac{2}{3}\)
Answer:
Given (0, 9) and m = \(\frac{2}{3}\)
The equation of a line is y = mx + b
Where,
m is the slope
b is the y-intercept
y = \(\frac{2}{3}\)x + b
Substitute the given point in the equation
9 = \(\frac{2}{3}\) (0) + b
9 = 0 + b
9 – 0 = b
b = 9
So, the equation of the line along with the y-intercept is y = \(\frac{2}{3}\)x + 9

Question 10.
ABSTRACT REASONING
Why does a horizontal line have a slope of 0, but a vertical line has an undefined slope?
Answer:
m = \(\frac{y2 – y1}{x2 – x1}\)
For a horizontal line,
The coordinates of y are the same. i.e.,
y1 = y2 = y3  ………
For a vertical line,
The coordinates of x are the same. i.e.,
x1 = x2 = x3 …….
The slope of the horizontal line (m) = \(\frac{y2 – y2}{x2 – x1}\)
The slope of the horizontal line (m) = 0
The slope of vertical line (m) = \(\frac{y2 – y1}{x2 – x1}\)
The slope of the vertical line (m) = Undefined

Parallel and Perpendicular Lines Mathematical Practices

Use a graphing calculator to graph the pair of lines. Use a square viewing window. Classify the lines as parallel, perpendicular, coincident, or non-perpendicular intersecting lines. Justify your answer.

Question 1.
x + 2y = 2
2x – y = 4
Answer:
The pair of lines are
x + 2y = 2
2x – y = 4
x + 2y = 2 ⇒ 2y = -x + 2 ⇒ y = -1/2 x + 1
2x – y = 4 ⇒ y = 2x – 4
The representation of the given pair of lines in the coordinate plane is:

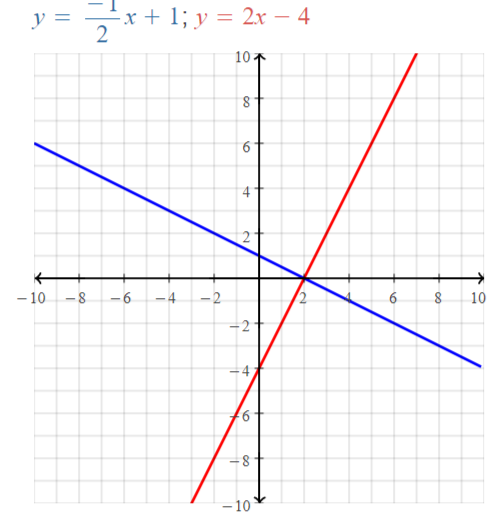
The product of the slope of the first line and the slope of the second line will be equal to -1
So,
By comparing the given pair of lines with
y = mx + b
We get
The slope of first line (m1) = –\(\frac{1}{2}\)
The slope of the second line (m2) = 2
m1 × m2 = –\(\frac{1}{2}\) × 2
m1m2 = -1
The given pair of lines are perpendicular lines.

Question 2.
x + 2y = 2
2x + 4y = 4
Answer:
The given pair of lines are:
x + 2y = 2 ⇒ 2y = -x + 2 ⇒ y = -1/2 x + 1
2x + 4y = 4 ⇒ y = -1/2 x + 1

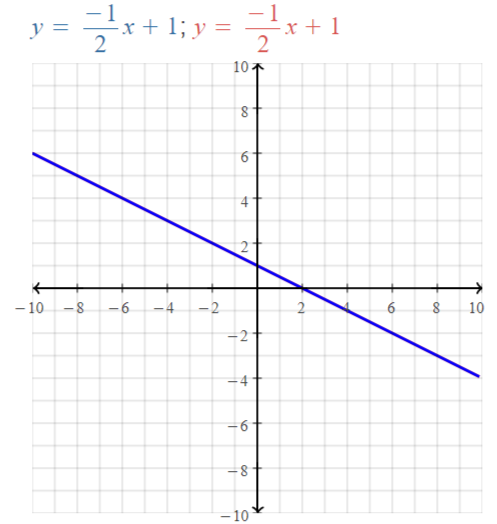
y = mx + b
m1 = –\(\frac{1}{2}\), b1 = 1
m2 = –\(\frac{1}{2}\), b2 = 1
So, the given pair of lines are coincident lines.

Question 3.
x + 2y = 2
x + 2y = – 2
Answer:
The given pair of lines are:
x + 2y = 2 ⇒ y = -1/2 x + 1
x + 2y = -2 ⇒ y = -1/2 x – 1

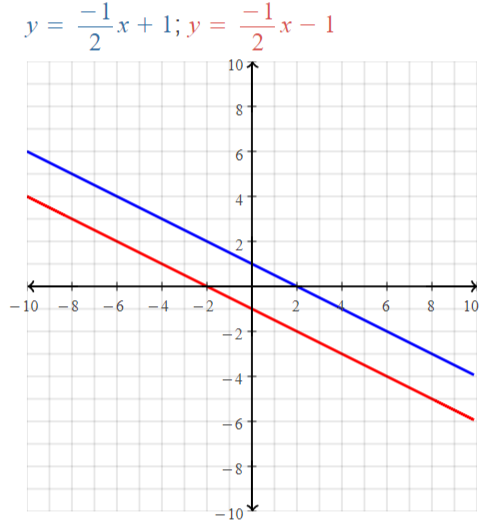
y = mx + b
We get
m1 = –\(\frac{1}{2}\), b1 = 1
m2 = \(\frac{1}{2}\), b2 = -1
From the graph, we observe that the given pair of lines are parallel lines

Question 4.
x – 2y = 2
x – y = – 4
Answer:
The given pair of lines are:
x – 2y = 2 ⇒ y = 1/2 x – 1
x – y = -4 ⇒ y = x + 4
Hence,
The representation of the given pair of lines in the coordinate plane is:

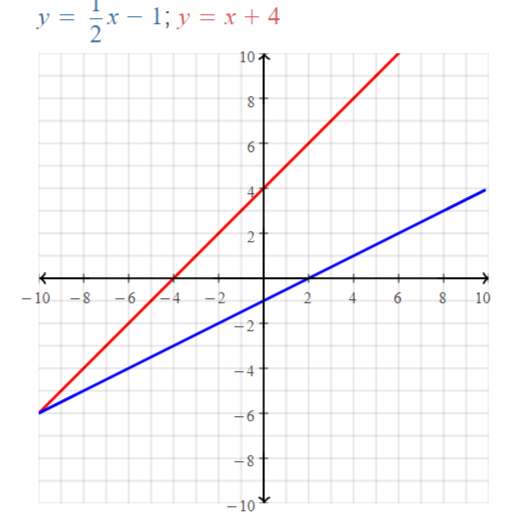
y = mx + b
The slope of first line (m1) = \(\frac{1}{2}\)
The slope of the second line (m2) = 1
m1m2  = \(\frac{1}{2}\)
From the above graph we observe that the given pair of lines are non-perpendicular lines

3.1 Pairs of Lines and Angles

Exploration 1

Points of intersection

work with a partner: Write the number of points of intersection of each pair of coplanar lines.

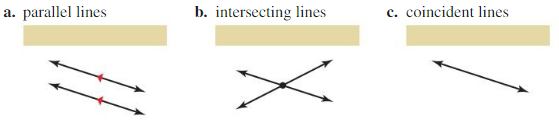
Answer:
a. The points of intersection of parallel lines:
The Parallel lines have the same slope but have different y-intercepts
We can say that any parallel line does not intersect at any point.
Parallel lines are those lines that are equidistant from each other and never meet.
We can say that the number of points of intersection of parallel lines is 0

b. The points of intersection of intersecting lines:
When two or more lines cross each other in a plane, they are called intersecting lines.
The number of points of intersection of intersecting lines is: 1

c. The points of intersection of coincident lines:
Intersecting lines have one point in common and coincident lines have infinitely many points in common.
Any coincident line does not intersect at any point or intersect at 1 point.
The number of points of intersection of coincident lines is: 0 or 1

Exploration 2

Classifying Pairs of Lines
Work with a partner: The figure shows a right rectangular prism. All its angles are right angles. Classify each of the following pairs of lines as parallel, intersecting, coincident, or skew. Justify your answers. (Two lines are skew lines when they do not intersect and are not coplanar.)


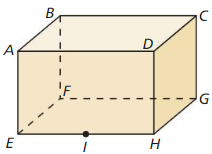
Answer:
The given rectangular prism is:


Parallel lines are those lines that are equidistant from each other and never meet.
Intersecting lines are those lines that intersect with each other and are in the same plane.
Coincident lines are the lines that lie on each other and in the same plane.
Skew lines are lines that do not intersect in the same plane and do not intersect.

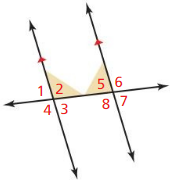
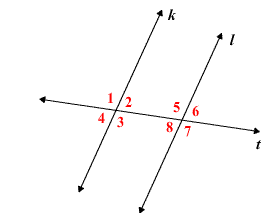
Exploration 3
Identifying Pairs of Angles
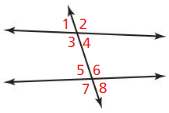
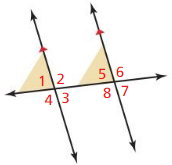
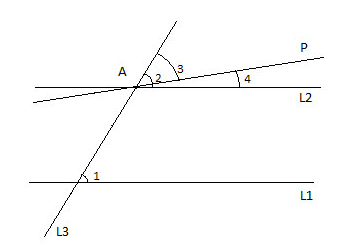
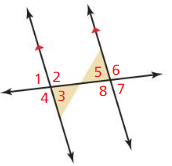
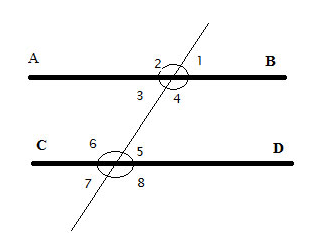
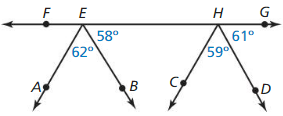
Work with a partner: In the figure, two parallel lines are intersected by a third line called a transversal.

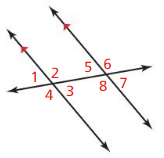
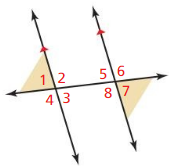
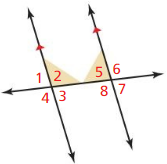
a. Identify all the pairs of vertical angles. Explain your reasoning.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to understand and use stated assumptions, definitions, and previously established results.
Answer:
The angles that are opposite to each other when two lines cross are called “Vertical angles”
From the figure,
∠1 and ∠3 are vertical angles
∠2 and ∠4 are vertical angles
∠5 and ∠7 are vertical angles
∠6 and ∠8 are vertical angles

b. Identify all the linear pairs of angles. Explain your reasoning.
Answer:
A “Linear pair” is a pair of adjacent angles formed when two lines intersect
From the figure,
∠1 and ∠2 linear pair of angles
∠4 and ∠3 linear pair of angles
∠5 and ∠6 linear pair of angles
∠8 and ∠7 linear pair of angles

Communicate Your Answer
Question 4.
What does it mean when two lines are parallel, intersecting, coincident, or skew?
Answer:

• Parallel: The two lines are said to be Parallel when they do not intersect each other and are coplanar.
• Intersecting: The two lines are said to be Intersecting lines when they intersect each other and are coplanar.
• Coincident: The two lines are said to be Coincident lines when they lie on each other and are coplanar. They are neither parallel nor perpendicular lines.
• Skew: The two lines are said to be Skewed when they do not intersect each other and are not parallel.

Question 5.
In Exploration 2. find more pairs of lines that are different from those given. Classify the pairs of lines as parallel, intersecting, coincident, or skew. Justify your answers.
Answer:
The given rectangular prism of Exploration 2 is:

The pair of lines that are different from the given pair of lines in Exploration 2 are:
a. \(\overline{C D}\) and \(\overline{A E}\)
b. \(\overline{D H}\) and \(\overline{F G}\)
a. \(\overline{C D}\) and \(\overline{A E}\) are “Skew lines” because they are not intersecting and are non-coplanar
b. \(\overline{D H}\) and \(\overline{F G}\) are “Skew lines” because they are not intersecting and are non-coplanar

Lesson 3.1 Pairs of Lines and Angles

Monitoring Progress

Question 1.
Look at the diagram in Example 1. Name the line(s) through point F that appear skew to .
Answer:
The line that passes through point F that appears skewed to is: \(\overline{F C}\)

Question 2.
In Example 2, can you use the Perpendicular Postulate to show that is not perpendicular to ? Explain why or why not.
Answer:
Perpendicular Postulate:
Perpendicular postulate states that if a line and a point are not on the line, then there is exactly one line through the point perpendicular to the given line.
\(\overline{A C}\) is not perpendicular to \(\overline{B F}\) because as per the perpendicular Postulate, \(\overline{A C}\) will be a straight line but it is not a straight line.
Hence we can use the “Perpendicular Postulate” to show that \(\overline{A C}\) is not perpendicular to \(\overline{B F}\)

Classify the pair of numbered angles.

Question 3.

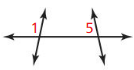
Answer:
Two angles that share a common vertex and side are called adjacent angles.
From the figure, we observe that ∠1 and ∠5 are the adjacent angles.

Question 4.

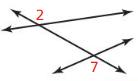
Answer:
Vertical angles are the angles that are opposite to each other where two lines cross.
From the figure, we observe that ∠2 and ∠7 are the “Vertical angles”

Question 5.

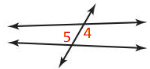
Answer:
Vertical angles are the angles that are opposite to each other where two lines cross.
From the figure, we observe that ∠4 and ∠5 are the “Vertical angles”

Exercise 3.1 Pairs of Lines and Angles

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
Two lines that do not intersect and are also not parallel are ________ lines.
Answer: Two lines that do not intersect and are also not parallel are skew lines.

Question 2.
WHICH ONE did DOESN’T BELONG?
Which angle pair does not belong with the other three? Explain our reasoning.

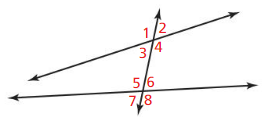
∠2 and ∠3
∠4 and ∠5
∠1 and ∠8
∠2 and∠7
Answer: ∠4 and ∠5 angle-pair does not belong with the other three

Explanation:
The angles that have a common side are called “Adjacent angles”
The angles that are opposite to each other when 2 lines cross are called “Vertical angles”
From the figure, we observe that,
∠2 and ∠3 are vertical angles
∠4 and ∠5 are adjacent angles
∠1 and ∠8 are vertical angles
∠2 and ∠7 are vertical angles
Thus, ∠4 and ∠5 angle-pair does not belong with the other three

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 6, think of each segment in the diagram as part of a line. All the angles are right angles. Which line(s) or plane(s) contain point B and appear to fit the description?

Question 3.
line(s) parallel to .
Answer:

Question 4.
line(s) PerPendicular to .
Answer:
The perpendicular lines are two lines that intersect each other and the angle formed between the two lines should be equal to 90 degrees.
The line that is perpendicular to \(\overline{C D}\) is: \(\overline{A D}\) and \(\overline{C B}\)

Question 5.
line(s) skew to
Answer:

Question 6.
plane(s) parallel to plane CDH
Answer:
The plane parallel to plane CDH is Plane BAE

In Exercises 7-10, Use the diagram.

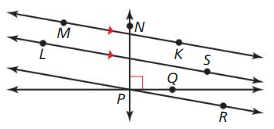
Question 7.
Name a pair of parallel lines.
Answer:

Question 8.
Name a pair of perpendicular lines.
Answer:
The perpendicular lines are two lines that intersect each other and the angle formed between the two lines should be equal to 90 degrees.
\(\overline{N P}\) and \(\overline{P O}\) are perpendicular lines

Question 9.

Answer:

Question 10.

Answer:
The perpendicular lines are two lines that intersect each other and the angle formed between the two lines should be equal to 90 degrees.
\(\overline{P R}\) and \(\overline{P O}\) are not perpendicular lines.

In Exercises 11-14, identify all pairs of angles of the given type.

Question 11.
corresponding
Answer:

Question 12.
alternate interior
Answer:
Alternate interior angles are the angles formed when a transversal intersects two coplanar lines.
So, the alternate interior angles are: ∠4 and ∠5; ∠3 and ∠6

Question 13.
alternate exterior
Answer:

Question 14.
consecutive interior
Answer:
The pair of angles on one side of the transversal and inside the two lines are called the Consecutive interior angles.
So, the consecutive interior angles are: ∠3 and ∠5; ∠4 and ∠6

USING STRUCTURE
In Exercises 15-18, classify the angle pair as corresponding. alternate interior, alternate exterior, or consecutive interior angles.

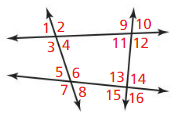
Question 15.
∠5 and ∠1
Answer:

Question 16.
∠11 and ∠13
Answer:
The pair of angles on one side of the transversal and inside the two lines are called the Consecutive interior angles.
So, the consecutive interior angles are: ∠11 and ∠13

Question 17.
∠6 and ∠13
Answer:

Question 18.
∠2 and ∠11
Answer:
∠2 and ∠11 are the Vertical angles
The angles that are opposite to each other when 2 lines cross are called “Vertical angles”

ERROR ANALYSIS
In Exercises 19 and 20. describe and correct the error in the conditional statement about lines.

Question 19.

Answer:

Question 20.

Answer:
Perpendicular postulate states that if a line and a point are not on the line, then there is exactly one line through the point perpendicular to the given line.
The statement is false.

Question 21.
MODELING WITH MATHEMATICS
Use the photo to decide whether the statement is true or false. Explain Your reasoning.

a. The plane containing the floor of the treehouse is parallel to the ground.
b. The lines containing the railings of the staircase, such as , are skew to all lines in the plane containing the ground.
c. All the lines containing the balusters. such as , are perpendicular to the plane containing the floor of the treehouse.
Answer:

Question 22.
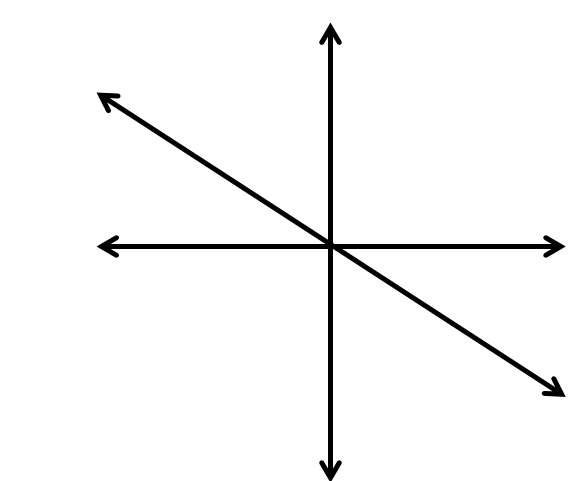
THOUGHT-PROVOKING
If two lines are intersected by a third line, is the third line necessarily a transversal? Justify your answer with a diagram.
Answer:
Parallel lines do not intersect each other
Perpendicular lines intersect at each other at right angles
The third intersecting line can intersect at the same point that the two lines have intersected as shown below:

Question 23.
MATHEMATICAL CONNECTIONS
Two lines are cut by a transversal. Is it possible for all eight angles formed to have the same measure? Explain your reasoning.
Answer:

Question 24.
HOW DO YOU SEE IT?
Think of each segment in the figure as part of a line.

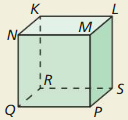
a. Which lines are parallel to ?
Answer:
The lines that do not intersect each other are called Parallel lines.
The line parallel to \(\overline{N Q}\) is \(\overline{M P}\)

b. Which lines intersect ?
Answer:
The lines that are coplanar and any two lines that have a common point are called Intersecting lines.
The lines that intersect are: \(\overline{Q P}\), \(\overline{N K}\), \(\overline{N M}\)

c. Which lines are skew to ?
Answer:
The lines that do not intersect or not parallel and are non-coplanar are called “Skew lines”
The lines that are skew to are \(\overline{K L}\), \(\overline{L M}\), and \(\overline{L S}\)

d. Should you have named all the lines on the cube in parts (a)-(c) except \(\overline{N Q}\)? Explain.
Answer:
No, we did not name all the lines on the cube in parts (a) – (c) except \(\overline{N Q}\)

In exercises 25-28. copy and complete the statement. List all possible correct answers.

Question 25.
∠BCG and __________ are corresponding angles.
Answer:

Question 26.
∠BCG and __________ are consecutive interior angles.
Answer:
∠BCG and ∠FCA and ∠BCA are consecutive interior angles.

Question 27.
∠FCJ and __________ are alternate interior angles.
Answer:

Question 28.
∠FCA and __________ are alternate exterior angles.
Answer:
∠FCA and ∠JCB are alternate exterior angles.

Question 29.
MAKING AN ARGUMENT
Your friend claims the uneven parallel bars in gymnastics are not really Parallel. She says one is higher than the other. so they cannot be on the same plane. Is she correct? Explain.

Answer:

Maintaining Mathematical Proficiency

Use the diagram to find the measure of all the angles.

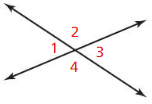
Question 30.
m∠1 = 76°
Answer:
Sum of the adjacent angles is: 180°
The adjacent angles are: ∠1 and ∠2; ∠2 and ∠3; ∠3 and ∠4; and ∠4 and ∠1
The vertical angles are: ∠1 and ∠3; ∠2 and ∠4
∠1 + ∠2 = 180°
∠2 = 180° – ∠1
= 180° – 76° = 104°
∠2 = 104°
∠3 = 76° and ∠4 = 104°
∠1 = 76°, ∠2 = 104°, ∠3 = 76°, and ∠4 = 104°

Question 31.
m∠2 = 159°
Answer:

3.2 Parallel Lines and Transversals

Exploration 1

Exploring parallel Lines

Work with a partner: Use dynamic geometry software to draw two parallel lines. Draw a third line that intersects both parallel lines. Find the measures of the eight angles that are formed. What can you conclude?

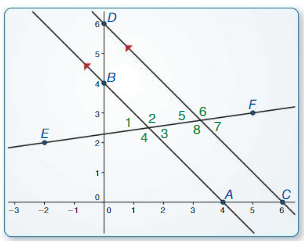
Answer:

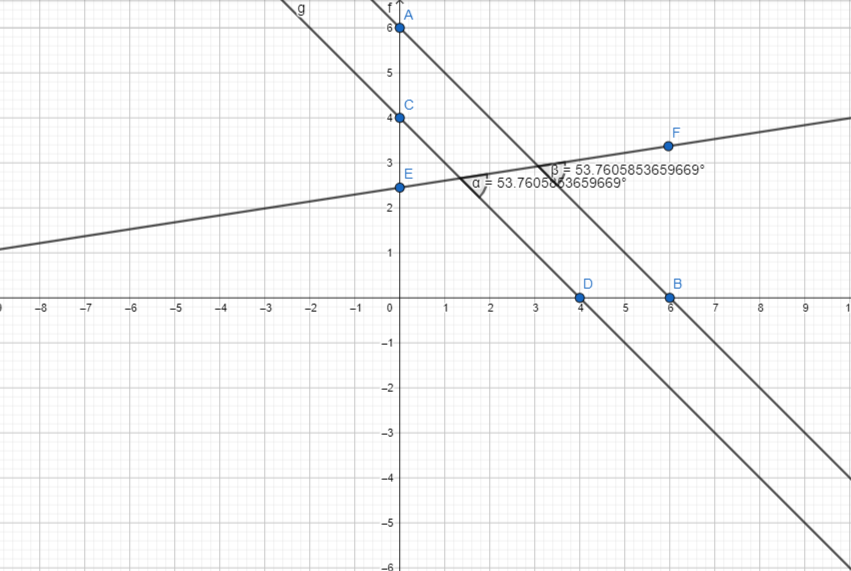
We observe that,
∠3 = 53.7° and ∠4 = 53.7°
The angle measures of the vertical angles are congruent
∠1 = 53.7° and ∠5 = 53.7°
Hence, ∠1 = ∠2 = ∠3 = ∠4 = ∠5 = ∠6 = ∠7 = 53.7°

Exploration 2

Writing conjectures

Work with a partner. Use the results of Exploration 1 to write conjectures about the following pairs of angles formed by two parallel lines and a transversal.
ATTENDING TO PRECISION
To be proficient in math, you need to communicate precisely with others.
a. corresponding angles

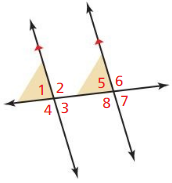
Answer:

When two lines are crossed by another line, the angles in matching corners are called “Corresponding angles”
From the figure,
∠1 and ∠5 are corresponding angles
∠4 and ∠8 are corresponding angles

b. alternate interior angles

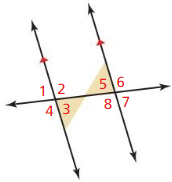
Answer:
Alternate Interior Angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal.
From the figure,
∠3 and ∠5 are alternate interior angles
∠2 and ∠8 are alternate interior angles

c. alternate exterior angles

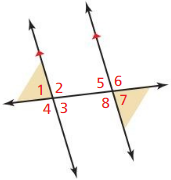
Answer:
Alternate exterior angles are the pair of angles that lie on the outer side of the two parallel lines but on either side of the transversal line.
From the figure,
∠1 and ∠7 alternate exterior angles
∠6 and ∠4 alternate exterior angles

d. consecutive interior angles

Answer:
When two lines are cut by a transversal, the pair of angles on one side of the transversal and inside the two lines are called the Consecutive interior angles.
∠2 and ∠5 consecutive interior angles
∠3 and ∠8 consecutive interior angles

Communicate Your Answer

Question 3.
When two parallel lines are cut by a transversal, which of the resulting pairs of angles are congruent?
Answer:
If two parallel lines are cut by a transversal, then the pairs of “Alternate exterior angles” are congruent.
If two parallel lines are cut by a transversal, then the pairs of “Corresponding angles” are congruent.
If two parallel lines are cut by a transversal, then the pairs of “Alternate interior angles” are congruent.

Question 4.
In Exploration 2. m∠1 = 80°. Find the other angle measures.
Answer:
Given,
m∠1 = 80°
All the angle measures are equal
∠1 = ∠2 = ∠3 = ∠4 = ∠5 = ∠6 = ∠7 = ∠8 = 80°

Lesson 3.2 Parallel Lines and Transversals

Monitoring Progress

Use the diagram

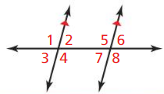
Question 1.
Given m∠1 = 105°, find m∠4, m∠5, and m∠8. Tell which theorem you use in each case.
Answer:

Given m∠1 = 105°
To find ∠4:
Verticle angle theorem:
Vertical Angles Theorem states that vertical angles, angles that are opposite each other and formed by two intersecting straight lines, are congruent
m∠1 = m∠4
m∠4 = 105°
To find ∠5:
Alternate Interior angles theorem:
The Alternate Interior Angles Theorem states that, when two parallel lines are cut by a transversal, the resulting alternate interior angles are congruent
m∠4 = m∠5
m∠5 = 105°
To find ∠8:
Verticle angle theorem:
Vertical Angles Theorem states that vertical angles, angles that are opposite each other and formed by two intersecting straight lines, are congruent.
m∠5 = m∠8
m∠8 = 105°

Question 2.
Given m∠3 = 68° and m∠8 = (2x + 4)°, what is the value of x? Show your steps.
Answer:
Given m∠3 = 68° and m∠8 = (2x + 4)°
∠3 and ∠8 are consecutive exterior angles.
If parallel lines are cut by a transversal line, then consecutive exterior angles are supplementary.
∠3 + ∠8 = 180°
68° + (2x + 4)° = 180°
2x + 72° = 180°
2x° = 180° – 72°
2x° = 108°
x = \(\frac{108}{2}\)
x = 54°

Question 3.
In the proof in Example 4, if you use the third statement before the second statement. could you still prove the theorem? Explain.
Answer:
If you even interchange the second and third statements, you could still prove the theorem as the second line before interchange is not necessary.
If you use the third statement before the second statement, you could still prove the theorem

Question 4.
WHAT IF?
In Example 5. yellow light leaves a drop at an angle of m∠2 = 41°. What is m∠1? How do you know?
Answer:
m∠2 = 41°
∠1 and ∠2, then they are alternate interior angles
Now,
According to the Alternate interior angle theorem,
∠1 = ∠2
∠2 = 41°
∠1 = 41°

Exercise 3.2 Parallel Lines and Transversals

Vocabulary and Core Concept Check

Question 1.
WRITING
How are the Alternate Interior Angles Theorem (Theorem 3.2) and the Alternate Exterior
Angles Theorem (Theorem 3.3) alike? How are they different?
Answer:

Question 2.
WHICH ONE did DOESN’T BELONG?
Which pair of angle measures does not belong with the other three? Explain.

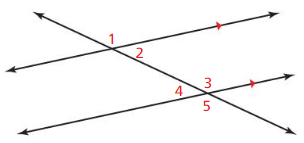
m∠1 and m∠3
m∠2 and m∠4
m∠2 and m∠3
m∠1 and m∠5
Answer:

From the figure we can find the vertical, alternate and consecutive angles
∠1 and ∠3 are vertical angles
∠2 and ∠4 are alternate interior angles
∠2 and ∠3 are consecutive interior angles
∠1 and ∠5 are alternate exterior angles
All the angles except ∠1 and ∠3 are the interior and exterior angles
∠1 and ∠3 pair does not belong with the other three.

Monitoring Progress and Modeling with Mathematics

In Exercises 3-6, find m∠1 and m∠2. Tell which theorem you use in each case.

Question 3.

Answer:

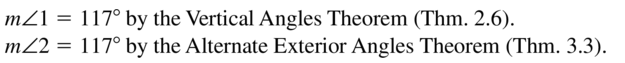
Question 4.

Answer:

From the figure,
∠1 = ∠2 (Vertical Angles theorem)
∠2 = 150° (Alternate exterior angles theorem)
∠1 = ∠2 = 150°

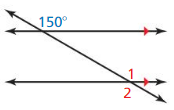
Question 5.

Answer:

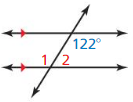
Question 6.

Answer:
From the figure,
∠1 + ∠2 = 180° (consecutive interior angles theorem)
∠2 = 140° (Vertical angles theorem)
∠1 = 180° – 140°
∠1 = 40°
∠1 = 40° and ∠2 = 140°

In Exercises 7-10. find the value of x. Show your steps.

Question 7.

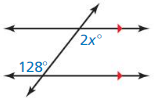
Answer:

Question 8.

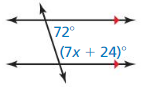
Answer:
From the figure,
72° + (7x + 24)° = 180° (Consecutive interior angles theory)
(7x + 24)° = 180° – 72°
(7x + 24)° = 108°
7x° = 108° – 24°
7x° = 84°
x° = \(\frac{84}{7}\)
x° = 12°

Question 9.

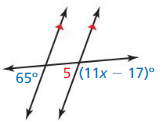
Answer:

Question 10.

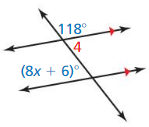
Answer:
From the figure,
(8x + 6)° = 118° (Vertical Angles theorem)
8x° = 118° – 6°
8x° = 112°
x° = \(\frac{112}{8}\)
x° = 14°

In Exercises 11 and 12. find m∠1, m∠2, and m∠3. Explain our reasoning.

Question 11.

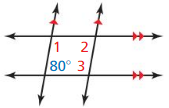
Answer:

Question 12.

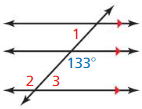
Answer:
From the figure,
∠3 + 133° = 180° (Consecutive Interior angles theorem)
∠3 = 180° – 133°
∠3 = 47°
∠2 + ∠3 = 180°
∠2 = 180° – ∠3
∠2 = 180° – 47°
∠2 = 133°
∠1 = ∠2
∠1 = ∠2 = 133° and ∠3 = 47°

Question 13.
ERROR ANALYSIS
Describe and correct the error in the students reasoning

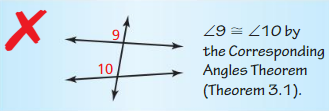
Answer:

Question 14.
HOW DO YOU SEE IT?
Use the diagram

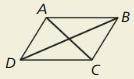
a. Name two pairs of congruent angles when \(\overline{A D}\) and \(\overline{B C}\) are parallel? Explain your reasoning.
Answer:
Let the congruent angle be ∠P
From the figure,
The pair of angles when \(\overline{A D}\) and \(\overline{B C}\) are parallel is ∠APB and ∠DPB

b. Name two pairs of supplementary angles when \(\overline{A B}\) and \(\overline{D C}\) are parallel. Explain your reasoning.
Answer:
The two pairs of supplementary angles when \(\overline{A B}\) and \(\overline{D C}\) are parallel is ∠ACD and ∠BDC

PROVING A THEOREM
In Exercises 15 and 16, prove the theorem.

Question 15.
Alternate Exterior Angles Theorem (Thm. 3.3)
Answer:

Question 16.
Consecutive Interior Angles Theorem (Thm. 3.4)
Answer:
Statement: If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles formed are supplementary
Proof:

Question 17.
PROBLEM-SOLVING
A group of campers ties up their food between two parallel trees, as shown. The rope is pulled taut. forming a straight line. Find m∠2. Explain our reasoning.

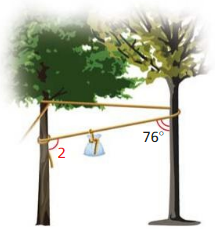
Answer:

Question 18.
DRAWING CONCLUSIONS
You are designing a box like the one shown.

a. The measure of ∠1 is 70°. Find m∠2 and m∠3.
b. Explain why ∠ABC is a straight angle.
c. If m∠1 is 60°, will ∠ABC still he a straight angle? Will the opening of the box be more steep or less steep? Explain.
Answer:

Question 19.
CRITICAL THINKING
Is it possible for consecutive interior angles to be congruent? Explain.
Answer:

Question 20.
THOUGHT-PROVOKING
The postulates and theorems in this book represent Euclidean geometry. In spherical geometry, all points are points on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere. In spherical geometry, is it possible that a transversal intersects two parallel lines? Explain your reasoning.
Answer: It is not possible that a transversal intersects two parallel lines

Explanation:
According to Euclidean geometry,
For a parallel line, there will be no intersecting point
But, In spherical geometry, even though there is some resemblance between circles and lines, there is no possibility to form parallel lines as the lines will intersect at least at 1 point on the circle which is called a tangent.
Hence, it is not possible that a transversal intersects two parallel lines.

MATHEMATICAL CONNECTIONS
In Exercises 21 and 22, write and solve a system of linear equations to find the values of x and y.

Question 21.

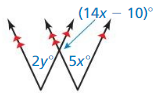
Answer:

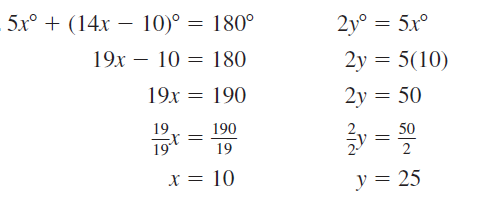
Question 22.

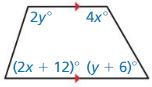
Answer:
From the figure,
2y° + 4x° = 180°
(2x + 12)° + (y + 6)° = 180°
2x° + y° + 18° = 180°
2x° + y° = 180° – 18°
2x° + y° = 162°———(1)
4x° + 2y° = 180°——–(2)
Solve eq. (1) & eq. (2)
2x° = 18°
x° = \(\frac{18}{2}\)
x° = 9°
Substitute the value of x to find y.
y° = 162° – 2 (9°)
y° = 162° – 18°
y° = 144°

Question 23.
MAKING AN ARGUMENT
During a game of pool. your friend claims to be able to make the shot Shown in the diagram by hitting the cue ball so that m∠1 = 25°. Is your friend correct? Explain your reasoning.

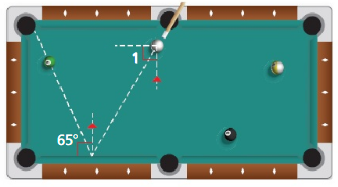
Answer:

Question 24.
REASONING
In diagram. ∠4 ≅∠5 and \(\overline{S E}\) bisects ∠RSF. Find m∠1. Explain your reasoning.

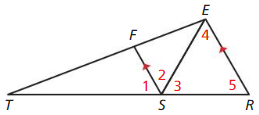
Answer:
Given,
∠4 ≅∠5 and \(\overline{S E}\) bisects ∠RSF
∠FSE = ∠ESR
From ΔESR,
Sum of the angle measures = 180°
∠3 + ∠4 + ∠5 = 180°
∠3 = 60° (∠4 ≅ ∠5 and the triangle is not a right triangle)
From the figure,
∠1 = ∠3 (Corresponding angles theorem)
∠1 = 60°

Maintaining Mathematical Proficiency

Write the converse of the conditional statement. Decide whether it is true or false.

Question 25.
If two angles are vertical angles. then they are congruent.
Answer:

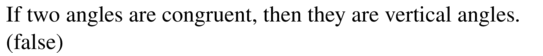
Question 26.
If you go to the zoo, then you will see a tiger.
Answer:
Statement: If you go to the zoo, then you will see a tiger
Converse: If you will see a tiger, then you go to the zoo (false).

Question 27.
If two angles form a linear pair. then they are supplementary.
Answer:

Question 28.
If it is warm outside, then we will go to the park.
Answer:
Statement: If it is warm outside, then we will go to the park
Converse: If you will go to the park, then it is warm outside (False).

3.3 Proofs with Parallel Lines

Exploration 1

Exploring Converses

Work with a partner: Write the converse of each conditional statement. Draw a diagram to represent the converse. Determine whether the converse is true. Justify your conclusion.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to make conjectures and build a logical progression of statements to explore the truth of your conjectures.

a. Corresponding Angles Theorem (Theorem 3.1): If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.

Converse:
If the pairs of corresponding angles are congruent, then the two parallel lines are cut by a transversal.
Answer:
The Converse of the Corresponding Angles Theorem says that if two lines and a transversal form congruent corresponding angles, then the lines are parallel.
When we compare the converses we obtained from the given statement and the actual converse,
The given statement is true.
Proof of Converse of Corresponding Angles Theorem:
Consider the 2 lines L1 and L2 intersected by a transversal line L3 creating 2 corresponding angles 1 and 2 which are congruent
We want to prove L1 and L2 are parallel and we will prove this by using “Proof of Contradiction”
According to Contradiction,
Let us assume L1 is not parallel to L2
According to the parallel line axiom, there is a different line than L2 that passes through the intersection point of L2 and L3, which is parallel to L1.
Let’s draw that line, and call it P. Let’s also call the angle formed by the traversal line and this new line angle 3, and we see that if we add some other angle, call it angle 4, to it, it will be the same as ∠2.
P || L1
∠1 ≅ ∠3,
m∠1=m∠3
∠1 and ∠2 are congruent
This contradiction means our assumption that L1 is not parallel to L2 is false, and so L1 must be parallel to L2.
The representation of the Converse of Corresponding Angles Theorem is:

b. Alternate Interior Angles Theorem (Theorem 3.2): If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent.

Converse:
If the pairs of alternate interior angles are congruent, then the two parallel lines are cut by a transversal.
Answer:
The converse of the Alternate Interior Angles Theorem states that if two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.
When we compare the actual converse and the converse according to the given statement,
The statement is false.

c. Alternate Exterior Angles Theorem (Theorem 3.3): If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent.

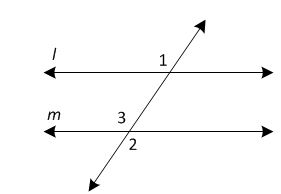
Converse:
If the pairs of alternate exterior angles are congruent, then the two parallel lines are cut by a transversal.
Answer:
The converse of the Alternate Exterior Angles Theorem states that if alternate exterior angles of two lines crossed by a transversal are congruent, then the two lines are parallel.
When we compare the converses we obtained from the given statement and the actual converse,
The given statement is true
Proof of Alternate exterior angles Theorem:
Given: ∠1 ≅ ∠2
Prove: l || m
The flow proof for the Converse of Alternate exterior angles Theorem is:

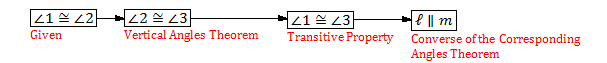
Converse of the Exterior angles Theorem:

d. Consecutive Interior Angles Theorem (Theorem 3.4): If two parallel lines are cut by a transversal. then the pairs of consecutive interior angles are supplementary.

Converse:
If the pairs of consecutive interior angles are supplementary, then the two parallel lines are cut by a transversal
Answer:
Converse of the consecutive Interior angles Theorem” states that if the consecutive interior angles on the same side of a transversal line intersecting two lines are supplementary, then the two lines are parallel.
When we compare the conversations we obtained from the given statement and the actual converse
We can conclude that the converse we obtained from the given statement is true
Proof of the Converse of the Consecutive Interior angles Theorem:
a.  m∠5 + m∠4 = 180° (From the given statement)
b.  m∠1 + m∠4 = 180° (Linear pair of angles are supplementary)
c. m∠5=m∠1 // (1), (2), transitive property of equality
d.  AB||CD (Converse of the Corresponding Angles Theorem)

Communicate Your Answer

Question 2.
For which of the theorems involving parallel lines and transversals is the converse true?
Answer:
The theorems involving parallel lines and transversals that the converse is true are:
a. Corresponding Angles Theorem
b. Alternate Exterior angles Theorem
c. Consecutive Interior angles Theorem

Question 3.
In Exploration 1, explain how you would prove any of the theorems that you found to be true.
Answer:
For the proofs of the theorems that you found to be true, refer to Exploration 1

Lesson 3.3 Proofs with Parallel Lines

Monitoring Progress

Question 1.
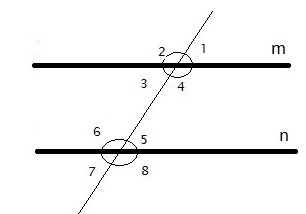
Is there enough information in the diagram to conclude that m || n? Explain.

Answer:
The given angles are the consecutive exterior angles
m || n
Converse of the Consecutive Exterior angles Theorem:
a.  m∠1 + m∠8 = 180° (From the given statement)
b.  m∠1 + m∠4 = 180° (Linear pair of angles are supplementary)
c. m∠5=m∠1 // (1), (2), transitive property of equality
d.  AB||CD (Converse of the Corresponding Angles Theorem)
The representation of the Converse of the Consecutive Interior angles Theorem is:

Question 2.
Explain why the Corresponding Angles Converse is the converse of the Corresponding Angles Theorem (Theorem 3.1).
Answer:
Corresponding Angles Postulate states that, when two parallel lines are cut by a transversal, the resulting corresponding angles are congruent
Converse: When the corresponding angles are congruent, the two parallel lines are cut by a transversal
The Converse of Corresponding Angles Theorem:
If the corresponding angles formed are congruent, then two lines l and m are cut by a transversal.
When we observe the Converse of the Corresponding Angles Theorem we obtained and the actual definition, both are the same.
The corresponding Angles Converse is the converse of the Corresponding Angles Theorem

Question 3.
If you use the diagram below to prove the Alternate Exterior Angles Converse. what Given and Prove statements would you use?

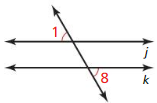
Answer:
It is given that the given angles are the alternate exterior angles.
Alternate Exterior angle Theorem:
If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent
Converse of the Alternate Exterior Angles Theorem:
Converse of the Alternate Exterior Angles Theorem states that if alternate exterior angles of two lines crossed by a transversal are congruent, then the two lines are parallel.
For the Converse of the alternate exterior angles Theorem,
The given statement is: ∠1 ≅ 8
To prove: l || k

Question 4.
Copy and complete the following paragraph proof of the Alternate Interior Angles Converse using the diagram in Example 2.
It is given that ∠4 ≅∠5. By the _______ . ∠1 ≅ ∠4. Then by the Transitive Property of Congruence (Theorem 2.2), _______ . So, by the _______ , g || h.
Answer:
It is given that ∠4 ≅∠5. By the Vertical Angles Congruence Theorem (Theorem 2.6). ∠1 ≅ ∠4. Then by the Transitive Property of Congruence (Theorem 2.2), ∠1 ≅∠5. So, by the Corresponding Angles Converse, g || h.

Question 5.
Each step is parallel to the step immediately above it. The bottom step is parallel to the ground. Explain why the top step is parallel t0 the ground.

Answer:
The steps are intersecting each other
In the same way, when we observe the floor from any step,
They are also parallel.
The top step is also parallel to the ground since they do not intersect each other at any point.

Question 6.
In the diagram below. p || q and q || r. Find m∠8. Explain your reasoning.

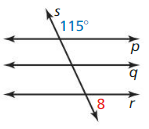
Answer:
The given angles are the consecutive exterior angles
∠8 + 115° = 180°
∠8 = 180° – 115°
∠8 = 65°

Exercise 3.3 Proofs with Parallel Lines

Vocabulary and Core Concept Check

Question 1.
VOCABULARY
Two lines are cut by a transversal. Which angle pairs must be congruent for the lines to be parallel?
Answer:

Question 2.
WRITING
Use the theorems from Section 3.2 and the converses of those theorems in this section to write three biconditional statements about parallel lines and transversals.
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3-8. find the value of x that makes m || n. Explain your reasoning.

Question 3.

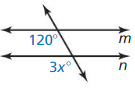
Answer:

Question 4.

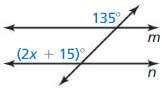
Answer:
According to the Corresponding Angles Theorem,
(2x + 15)° = 135°
2x° = 135° – 15°
2x° = 120°
x° = \(\frac{120}{2}\)
x° = 60°

Question 5.

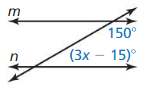
Answer:

Question 6.

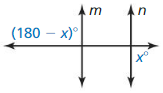
Answer:
According to the Corresponding Angles Theorem,
(180 – x)° = x°
180° = x°  + x°
2x° = 180°
x° = \(\frac{180}{2}\)
x° = 90°

Question 7.

Answer:

Question 8.

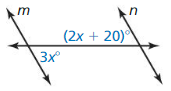
Answer:
According to the Corresponding Angles Theorem,
(2x + 20)° = 3x°
20° = 3x°  – 2x°
x° = 20°

In Exercises 9 and 10, use a compass and straightedge to construct a line through point P that is parallel to line m.

Question 9.

Answer:

Question 10.

Answer:
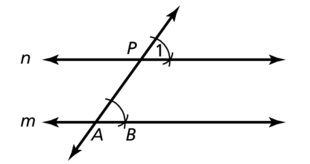
Let A and B be two points on line m.
Draw \(\overline{A P}\) and construct an angle ∠1 on n at P so that ∠PAB and ∠1 are corresponding angles

PROVING A THEOREM
In Exercises 11 and 12. prove the theorem.
Question 11.
Alternate Exterior Angles Converse (Theorem 3.7)
Answer:

Question 12.
Consecutive Interior Angles Converse (Theorem 3.8)
Answer:
Proof of the Converse of the Consecutive Interior angles Theorem:
Given: m∠5 + m∠4 = 180°
Prove: AB || CD

Now,
a.  m∠5 + m∠4 = 180° (From the given statement)
b.  m∠1 + m∠4 = 180° (Linear pair of angles are supplementary)
c. m∠5=m∠1 // (1), (2), transitive property of equality
d.  AB||CD (Converse of the Corresponding Angles Theorem)

In Exercises 13-18. decide whether there is enough information to prove that m || n. If so, state the theorem you would use.

Question 13.

Answer:

Question 14.

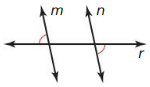
Answer:
Yes, there is enough information to prove m || n
The theorem we can use to prove that m || n is: Alternate Exterior angles Converse theorem

Question 15.

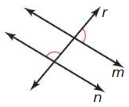
Answer:

Question 16.

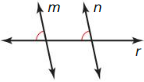
Answer:
No, there is not enough information to prove m || n

Question 17.

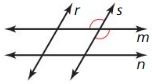
Answer:

Question 18.

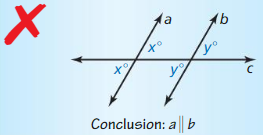
Answer:
Yes, there is enough information to prove m || n

ERROR ANALYSIS
In Exercises 19 and 20, describe and correct the error in the reasoning.

Question 19.

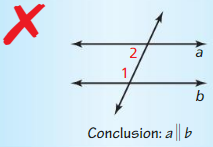
Answer:

Question 20.

Answer:
∠1 and ∠2 are Consecutive Interior angles
It also shows that a and b are cut by a transversal and they have the same length.
From the converse of the Consecutive Interior angles Theorem,
a || b

In Exercises 21-24. are and parallel? Explain your reasoning.

Question 21.

Answer:

Question 22.

Answer:
From the figure,
The sum of the given angle measures = 180°
The given angles are consecutive exterior angles
From the Consecutive Exterior angles Converse,
AC || DF

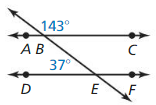
Question 23.

Answer:

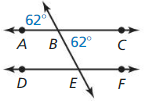
Question 24.

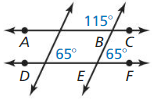
Answer:
From the figure,
We can observe that the sum of the angle measures of all the pairs i.e., (115 + 65)°, (115 + 65)°, and (65 + 65)° is not 180°
The sum of the angle measures is not supplementary, according to the Consecutive Exterior Angles Converse,
AC is not parallel to DF

Question 25.
ANALYZING RELATIONSHIPS
The map shows part of Denser, Colorado, Use the markings on the map. Are the numbered streets parallel to one another? Explain your reasoning.

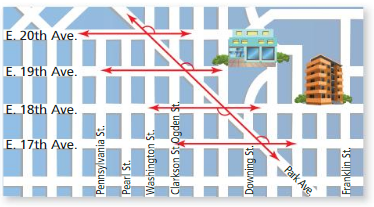
Answer:

Question 26.
ANALYZING RELATIONSHIPS
Each rung of the ladder is parallel to the rung directly above it. Explain why the top rung is parallel to the bottom rung.

Answer:
Given,
Each rung of the ladder is parallel to the rung directly above it.
The rungs are not intersecting at any point i.e., they have different points
The parallel lines do not have any intersecting points
We can conclude that the top rung is parallel to the bottom rung.

Question 27.
MODELING WITH MATHEMATICS
The diagram of the control bar of the kite shows the angles formed between the Control bar and the kite lines. How do you know that n is parallel to m?

Answer:

Question 28.
REASONING
Use the diagram. Which rays are parallel? Which rays are not parallel? Explain your reasoning.

Answer:

Question 29.
ATTENDING TO PRECISION
Use the diagram. Which theorems allow you to conclude that m || n? Select all that apply. Explain your reasoning.

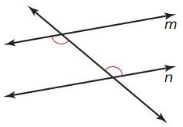
(A) Corresponding Angles Converse (Thm 3.5)
(B) Alternate Interior Angles Converse (Thm 3.6)
(C) Alternate Exterior Angles Converse (Thm 3.7)
(D) Consecutive Interior Angles Converse (Thm 3.8)
Answer:

Question 30.
MODELING WITH MATHEMATICS
One way to build stairs is to attach triangular blocks to angled support, as shown. The sides of the angled support are parallel. If the support makes a 32° angle with the floor, what must m∠1 so the top of the step will be parallel to the floor? Explain your reasoning.

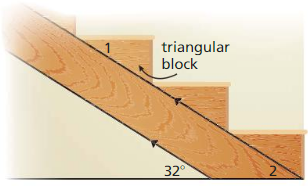
Answer:
It is given that the sides of the angled support are parallel and the support makes a 32° angle with the floor.
To make the top of the step where ∠1 is present to be parallel to the floor, the angles must be “Alternate Interior angles”
Alternate Interior angles are congruent.
∠1 = 32°

Question 31.
ABSTRACT REASONING
In the diagram, how many angles must be given to determine whether j || k? Give four examples that would allow you to conclude that j || k using the theorems from this lesson.

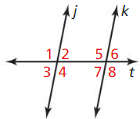
Answer:

Question 32.
THOUGHT-PROVOKING
Draw a diagram of at least two lines cut by at least one transversal. Mark your diagram so that it cannot be proven that any lines are parallel. Then explain how your diagram would need to change in order to prove that lines are parallel.
Answer:
The diagram that represents the figure that it can not be proven that any lines are parallel is:

From the above,
The diagram can be changed by the transformation of transversals into parallel lines and a parallel line into transversal

PROOF
In Exercises 33-36, write a proof.

Question 33.
Given m∠1 = 115°, m∠2 = 65°
Prove m||n

Answer:

Question 34.
Given ∠1 and ∠3 are supplementary.
Prove m||n

Answer:
Given: ∠1 and ∠3 are supplementary
To Prove: m || n

Question 35.
Given ∠1 ≅ ∠2, ∠3 ≅ ∠4
Prove \(\overline{A B} \| \overline{C D}\)

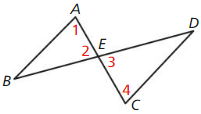
Answer:

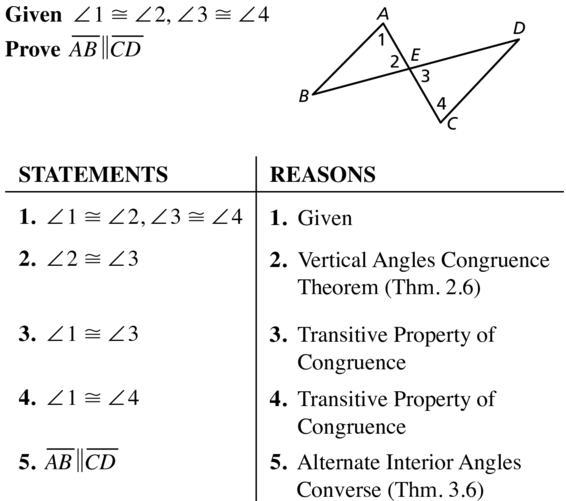
Question 36.
Given a||b, ∠2 ≅ ∠3
Prove c||d

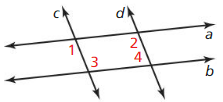
Answer:
Given: a || b, ∠2 ≅ ∠3
Prove: c || d
Hence,

Question 37.
MAKING AN ARGUMENT
Your classmate decided that based on the diagram. Is your classmate correct? Explain your reasoning.

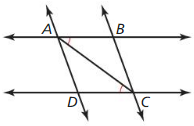
Answer:

Question 38.
HOW DO YOU SEE IT?
Are the markings on the diagram enough to conclude that any lines are parallel? If so. which ones? If not, what other information is needed?

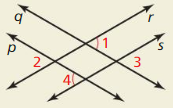
Answer:

∠1 and ∠4 are the pairs of corresponding angles
∠2 and ∠3 are the pairs of corresponding angles
According to the Converse of the Corresponding angles Theorem,
If the corresponding angles are congruent, then the two lines that are cut by a transversal are parallel lines
We can say that p and q; r and s are the pairs of parallel lines

Question 39.
PROVING A THEOREM
Use these steps to prove the Transitive Property of Parallel Lines Theorem
a. Cops the diagram with the Transitive Property of Parallel Lines Theorem on page 141.
b. Write the Given and Prove statements.
c. Use the properties of angles formed by parallel lines cut by a transversal to prove the theorem.
Answer:

Question 40.
MATHEMATICAL CONNECTIONS
Use the diagram

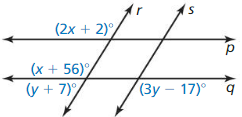
a. Find the value of x that makes p || q.
Answer:
From the figure,
p || q,
(2x + 2)° and (x + 56)°
We can observe that the given angles are corresponding angles
(2x + 2)° = (x + 56)°
2x – x = 56° – 2°
x° = 54°

b. Find the value of y that makes r || s.
Answer:
r || s,
The angles are (y + 7)° and (3y – 17)°
We can observe that the given angles are corresponding angles
(y + 7)° = (3y – 17)°
y – 3y = -17° – 7°
-2y° = -24°
y = \(\frac{24}{2}\)
y = 12°

c. Can r be parallel to s and can p, be parallel to q at the same time? Explain your reasoning.
Answer:
No, p ||q and r ||s will not be possible at the same time because when p || q, r, and s can act as transversal and when r || s, p, and q can act as transversal

Maintaining Mathematical Proficiency
Use the Distance Formula to find the distance between the two points.

Question 41.
(1, 3) and (- 2, 9)
Answer:

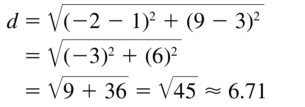
Question 42.
(- 3, 7) and (8, – 6)
Answer:
(-3, 7), and (8, -6)
Compare the given points with (x1, y1), and (x2, y2)
We know that,
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
d = \(\sqrt{(8 + 3)² + (7 + 6)²}\)
d = \(\sqrt{(11)² + (13)²}\)
d = \(\sqrt{290}\)
d = 17.02

Question 43.
(5, – 4) and (0, 8)
Answer:

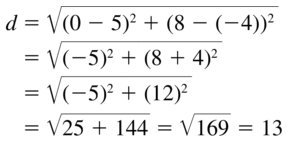
Question 44.
(13, 1) and (9, – 4)
Answer:
(13, 1), and (9, -4)
Compare the given points with (x1, y1), and (x2, y2)
We know that,
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
d = \(\sqrt{(13 – 9)² + (1 + 4)²}\)
d = \(\sqrt{(4)² + (5)²}\)
d = \(\sqrt{41}\)
d = 6.40

3.1 – 3.3 Study Skills: Analyzing Your Errors

Mathematical Practices

Question 1.
Draw the portion of the diagram that you used to answer Exercise 26 on page 130.
Answer:

Question 2.
In Exercise 40 on page 144. explain how you started solving the problem and why you started that way.
Answer:
You started solving the problem by considering the 2 lines parallel and two lines as transversals
If p and q are the parallel lines, then r and s are the transversals
If r and s are the parallel lines, then p and q are the transversals

3.1 – 3.3 Quiz

Think of each segment in the diagram as part of a line. Which lines(s) or plane(s) contain point G and appear to fit the description?

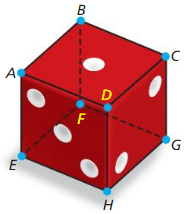
Question 1.
line(s) parallel to .
Answer:
The line parallel to is \(\overline{D H}\)

Question 2.
line(s) perpendicular to .
Answer:
The lines perpendicular to are \(\overline{F B}\) and \(\overline{F G}\)

Question 3.
line(s) skew to .
Answer:
The lines skew to are \(\overline{C D}\), \(\overline{C G}\), and \(\overline{A E}\)

Question 4.
plane(s) parallel to plane ADE
Answer:
The plane parallel to plane ADE is plane GCB

Identify all pairs of angles of the given type.

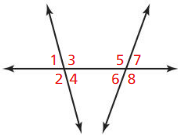
Question 5.
consecutive interior
Answer:
When two lines are cut by a transversal, the pair of angles on one side of the transversal and inside the two lines are known as consecutive interior angles.
The consecutive interior angles are 3 and 5, 4 and 6

Question 6.
alternate interior
Answer:
Alternate Interior Angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal.
The alternate interior angles are 3 and 6, 4 and 5

Question 7.
corresponding
Answer:
When two lines are crossed by another line, the angles in matching corners are called corresponding angles.
The corresponding angles are ∠1 and ∠5, ∠3 and ∠7, ∠2 and ∠4, ∠6 and ∠8.

Question 8.
alternate exterior
Answer:
Alternate exterior angles are the pair of angles that lie on the outer side of the two parallel lines but on either side of the transversal line.
The alternate exterior angles are ∠1 and ∠8, ∠7 and ∠2

Find m∠1 and m∠2. Tell which theorem you use in each case.

Question 9.

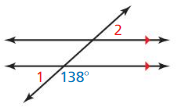
Answer:
From the figure,
By using the linear pair theorem,
∠1 + 138° = 180°
∠1 = 180° – 138°
∠1 = 42°
By using the Alternate Exterior Angles Theorem,
∠1 = ∠2
∠1 = ∠2 = 42°

Question 10.

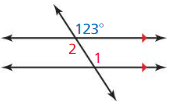
Answer:
From the figure,
By using the Vertical Angles Theorem,
∠2 = 123°
By using the vertical Angles Theorem,
∠1 = ∠2
∠1 = ∠2 = 123°

Question 11.

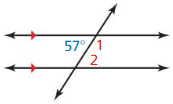
Answer:
From the figure,
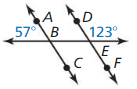
By using the linear pair theorem,
∠1 + 57° = 180°
∠1 = 180° – 57°
∠1 = 123°
By using the consecutive interior angles theorem,
∠1 + ∠2 = 180°
∠2 = 180° – 123°
∠2 = 57°
∠1 = 123° and ∠2 = 57°

Decide whether there is enough information to prove that m || n. If so, state the theorem you would use.

Question 12.

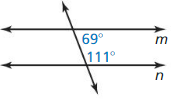
Answer:
By using the Consecutive Interior angles Converse
If the angle measure of the angles is a supplementary angle, then the lines cut by a transversal are parallel
69° + 111° = 180°
Hence, m || n by using the Consecutive Interior angles Theorem.

Question 13.

Answer:
By using the Corresponding Angles Theorem,
If the corresponding angles are congruent, then the lines cut by a transversal are parallel
Hence, m || n by using the Corresponding Angles Theorem

Question 14.

Answer:
From the figure,
It is given that l || m and l || n
By using the parallel lines property
If a || b and b || c, then a || c
Hence m || n

Question 15.
Cellular phones use bars like the ones shown to indicate how much signal strength a phone receives from the nearest service tower. Each bar is parallel to the bar directly next to it.

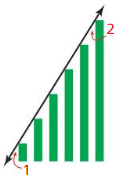
a. Explain why the tallest bar is parallel to the shortest bar.
Answer:
From the given bars,
We can observe that there is no intersection between any bars
If we represent the bars in the coordinate plane, we can observe that the number of intersection points between any bar is 0
The number of intersection points for parallel lines is 0
The tallest bar is parallel to the shortest bar.

b. Imagine that the left side of each bar extends infinitely as a line.
If m∠1 = 58°, then what is m∠2?
Answer:
Given, m∠1 = 58°
∠1 and ∠2 are the consecutive interior angles
The sum of the angle measure between 2 consecutive interior angles is 180°
∠1 + ∠ 2 = 180°
58 + ∠ 2 = 180°
∠2 = 180° – 58°
∠2 = 122°

Question 16.
The diagram shows lines formed on a tennis court.

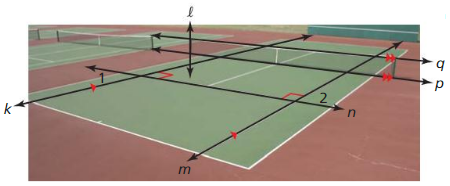
a. Identify two pairs of parallel lines so that each pair is in a different plane.
Answer:
There are a total of 5 lines.
The two pairs of parallel lines so that each pair is in a different plane are q and p, k and m

b. Identify two pairs of perpendicular lines.
Answer:
There are 2 perpendicular lines
The two pairs of perpendicular lines are l and n

c. Identify two pairs of skew line
Answer:
There are 2 pairs of skew lines
The 2 pairs of skew lines are q and p, l and m

d. Prove that ∠1 ≅ ∠2.
Answer:
∠1 and ∠2 are the alternate exterior angles
If the line cut by a transversal is parallel, then the corresponding angles are congruent
∠1 ≅ ∠2 (Alternate Exterior angles Theorem)

3.4 Proofs with Perpendicular Lines

Exploration 1

Writing Conjectures

Work with a partner: Fold a piece of pair in half twice. Label points on the two creases. as shown.

a. Write a conjecture about \(\overline{A B}\) and \(\overline{C D}\). Justify your conjecture.
Answer:
The conjecture about \(\overline{A B}\) and \(\overline{c D}\) is “If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular.”

b. Write a conjecture about \(\overline{A O}\) and \(\overline{O B}\) Justify your conjecture.
Answer:
The conjecture about \(\overline{A O}\) and \(\overline{O B}\) is “In a plane, if two lines are perpendicular to the same line, then they are parallel to each other.”

Exploration 2

Exploring a segment Bisector

Work with a partner: Fold and crease a piece of paper. as shown. Label the ends of the crease as A and B.

a. Fold the paper again so that point A coincides with point B. Crease the paper on that fold.
Answer:

b. Unfold the paper and examine the four angles formed by the two creases. What can you conclude about the four angles?
Answer:
When we unfold the paper and examine the four angles formed by the two creases, we can say that the four angles formed are the right angles i.e., 90°

Exploration 3

Writing a conjecture

Work with a partner.

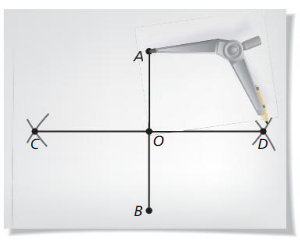
a. Draw \(\overline{A B}\), as shown.
b. Draw an arc with center A on each side of AB. Using the same compass selling, draw an arc with center B on each side \(\overline{A B}\). Label the intersections of arcs C and D.
c. Draw \(\overline{C D}\). Label its intersection with \(\overline{A B}\) as O. Write a conjecture about the resulting diagram. Justify your conjecture.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to make conjectures and build a logical progression of statements to explore the truth of your conjectures.
Answer:
The resultant diagram is:

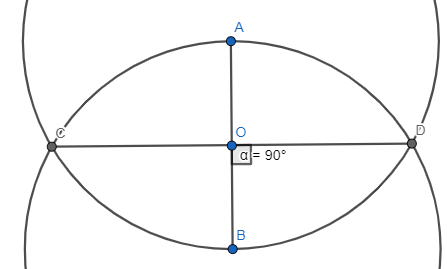
The angles formed at all the intersection points are: 90°
The lengths of the line segments are equal i.e., AO = OB and CO = OD

Communicate Your Answer

Question 4.
What conjectures can you make about perpendicular lines?
Answer:
1. If two lines intersect to form a linear pair of congruent angles, then the lines are said to be perpendicular lines.
2. If a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other line.
3. If two lines are perpendicular to the same line, then they are parallel to each other.

Question 5.
In Exploration 3. find AO and OB when AB = 4 units.
Answer:
AB = AO + OB
AO = OB
AB = 4 units
The values of AO and OB are: 2 units

Lesson 3.4 Proofs with Perpendicular Lines

Monitoring Progress

Question 1.
Find the distance from point E to

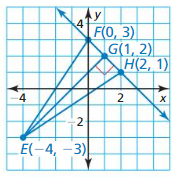
Answer:
Given E is ⊥ to \(\overline{F H}\)
To find the distance between E and \(\overline{F H}\), we need to find the distance between E and G i.e., EG
From the coordinate plane,
E (-4, -3), G (1, 2)
Compare the given points with
E (x1, y1), G (x2, y2)
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
d = \(\sqrt{(1 + 4)² + (2 + 3)²}\)
d = \(\sqrt{(5)² + (5)²}\)
d = \(\sqrt{50}\)
d = 7.07

Question 2.
Prove the Perpendicular Transversal Theorem using the diagram in Example 2 and the Alternate Exterior Angles Theorem (Theorem 3.3).
Answer:In a plane, if a line is perpendicular to one of the two parallel lines, then it is perpendicular to the other line also

Proof:
Given: k || l, t ⊥ k
Prove: t ⊥ l

Alternate Exterior Angles Theorem:
When two parallel lines are cut by a transversal, the resulting alternate exterior angles are congruent.

Proof:
Given: k || l
Prove: ∠1 ≅ ∠7 and ∠4 ≅ ∠6
Since k || l, by the Corresponding Angles Postulate,
∠1 ≅ ∠5
Also, by the Vertical Angles Theorem,
∠5 ≅ ∠7
Then, by the Transitive Property of Congruence,
∠1 ≅ ∠7
You can prove that ∠4 and ∠6 are congruent using the same method.

Use the lines marked in the photo.

Question 3.
Is b || a? Explain your reasoning.
Answer:
a and b are nonintersecting lines.
b || a

Question 4.
Is b ⊥ c? Explain your reasoning.
Answer:
The angle between b and c is 90°
Hence, b is perpendicular to c

Exercise 3.4 Proofs with Perpendicular Lines

Vocabulary and core Concept Check

Question 1.
COMPLETE THE SENTENCE
The perpendicular bisector of a segment is the line that passes through the _______________ of the segment at a _______________ angle.
Answer:

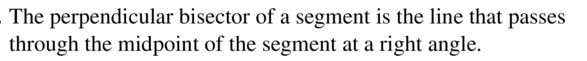
Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

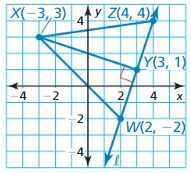
Find the distance from point X to
Answer:
X (-3, 3), Y (3, 1)
Compare the given points with
(x1, y1), (x2, y2)
We know that,
XY = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
XY = \(\sqrt{(3 + 3)² + (3 – 1)²}\)
XY = \(\sqrt{(6)² + (2)²}\)
XY = 6.32

Find XZ
Answer:
The given points are:
X (-3, 3), Z (4, 4)
Compare the given points with
(x1, y1), (x2, y2)
We know that,
XZ = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
XZ = \(\sqrt{(4 + 3)² + (3 – 4)²}\)
XZ = \(\sqrt{(7)² + (1)²}\)
XZ = 7.07

Find the length of \(\overline{X Y}\)
Answer:
The given points are:
X (-3, 3), Y (3, 1)
Compare the given points with
(x1, y1), (x2, y2)
We know that,
XY = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
XY = \(\sqrt{(3 + 3)² + (3 – 1)²}\)
XY = \(\sqrt{(6)² + (2)²}\)
XY = 6.32

Find the distance from line l to point X.
Answer:
The given points are:
X (-3, 3), Y (3, 1)
Compare the given points with
(x1, y1), (x2, y2)
We know that,
XY = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
XY = \(\sqrt{(3 + 3)² + (3 – 1)²}\)
XY = \(\sqrt{(6)² + (2)²}\)
XY = 6.32

Monitoring Progress and Modeling with Mathematics

In Exercises 3 and 4. find the distance from point A to .

Question 3.

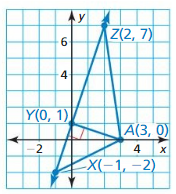
Answer:

Question 4.

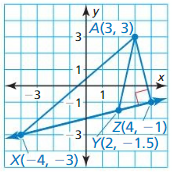
Answer:
The given points are:
X (3, 3), Y (2, -1.5)
Compare the given points with
(x1, y1), (x2, y2)
We know that,
XY = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
XY = \(\sqrt{(3 + 1.5)² + (3 – 2)²}\)
XY = \(\sqrt{(4.5)² + (1)²}\)
XY = 4.60

CONSTRUCTION
In Exercises 5-8, trace line m and point P. Then use a compass and straightedge to construct a line perpendicular to line m through point P.

Question 5.

Answer:

Question 6.

Answer:
1. Using P as the center, draw two arcs intersecting with line m.
2. Label the intersections as points X and Y.
3. Using X and Y as centers and an appropriate radius, draw arcs that intersect.
4. Label the intersection as Z. Draw \(\overline{P Z}\)

Question 7.

Answer:

Question 8.

Answer:
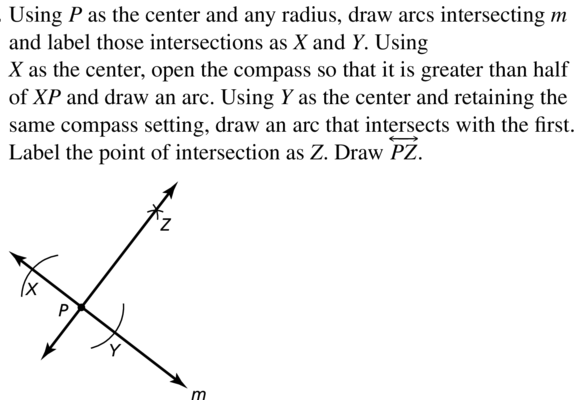
1. Using P as the center and any radius, draw arcs intersecting m and label those intersections as X and Y.
2. Using X as the center, open the compass so that it is greater than half of XP and draw an arc.
3. Using Y as the center and retaining the same compass setting, draw an arc that intersects with the first
4. Label the point of intersection as Z. Draw \(\overline{P Z}\)

CONSTRUCTION
In Exercises 9 and 10, trace \(\overline{A B}\). Then use a compass and straightedge to construct the perpendicular bisector of \(\overline{A B}\)

Question 9.

Answer:

Question 10.

Answer:
Using a compass setting greater than half of AB, draw two arcs using A and B as centers
Connect the points of intersection of the arcs with a straight line

ERROR ANALYSIS
In Exercises 11 and 12, describe and correct the error in the statement about the diagram.
Question 11.

Answer:

Question 12.

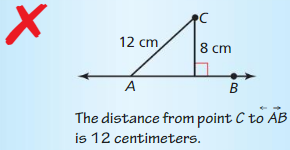
Answer:
The distance from the perpendicular to the line is given as the distance between the point and the non-perpendicular line
The distance from point C to AB is the distance between point C and A i.e., AC
Hence, the distance from point C to AB is 12 cm

PROVING A THEOREM 
In Exercises 13 and 14, prove the theorem.
Question 13.
Linear Pair Perpendicular Theorem (Thm. 3. 10)
Answer:

Question 14.
Lines Perpendicular to a Transversal Theorem (Thm. 3.12)
Answer:
In a plane, if a line is perpendicular to one of the two parallel lines, then it is perpendicular to the other line also

Proof:
Given: k || l, t ⊥ k
Prove: t ⊥ l

PROOF
In Exercises 15 and 16, use the diagram to write a proof of the statement.

Question 15.
If two intersecting lines are perpendicular. then they intersect to form four right angles.
Given a ⊥ b
Prove ∠1, ∠2, ∠3, and ∠4 are right angles.

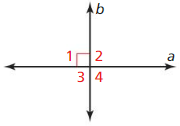
Answer:

Question 16.
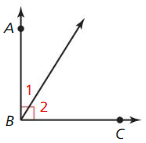
If two sides of two adjacent acute angles are perpendicular, then the angles are complementary.
Given \(\overrightarrow{B A}\) ⊥\(\vec{B}\)C
Prove ∠1 and ∠2 are complementary

Answer:

In Exercises 17-22, determine which lines, if any, must be parallel. Explain your reasoning.

Question 17.

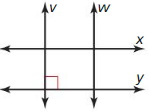
Answer:

Question 18.

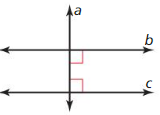
Answer:
From the figure, we observe that a is perpendicular to both lines b and c
By using the Perpendicular transversal theorem, a is both perpendicular to b and c and b is parallel to c

Question 19.

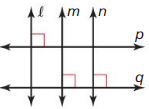
Answer:

Question 20.

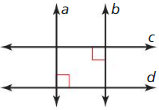
Answer:
From the figure, we can observe that a is perpendicular to d and b is perpendicular to c.
By using the Perpendicular transversal theorem, a is perpendicular to d and b is perpendicular to c.

Question 21.

Answer:

Question 22.

Answer:
From the figure,
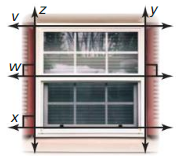
w ⊥ v and w⊥ y
We can say that w and v are parallel lines by the “Perpendicular Transversal Theorem”
z ⊥ x and w ⊥ z
We can say that w and x are parallel lines by the “Perpendicular Transversal theorem”

Question 23.
USING STRUCTURE
Find all the unknown angle measures in the diagram. Justify your answer for cacti angle measure.

Answer:

Question 24.
MAKING AN ARGUMENT
Your friend claims that because you can find the distance from a point to a line, you should be able to find the distance between any two lines. Is your friend correct? Explain your reasoning.
Answer:
It is given your friend claims that because you can find the distance from a point to a line, you should be able to find the distance between any two lines.

Your friend is not correct.

Question 25.
MATHEMATICAL CONNECTIONS
Find the value of x when a ⊥ b and b || c.

Answer:

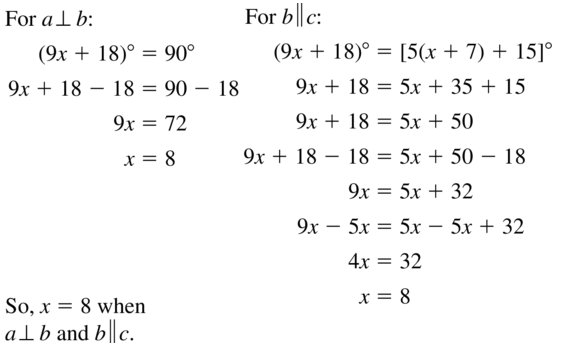
Question 26.
HOW DO YOU SEE IT?
You are trying to cross a stream from point A. Which point should you jump to in order to jump the shortest distance? Explain your reasoning.

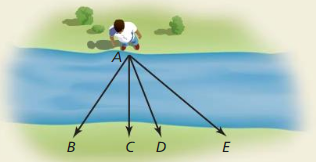
Answer:
From the figure,
Point A is perpendicular to Point C.
According to Perpendicular Transversal Theorem,
The distance between the perpendicular points is the shortest.
In order to jump the shortest distance, you have to jump to point C from point A

Question 27.
ATTENDING TO PRECISION
In which of the following diagrams is \(\overline{A C}\) || \(\overline{B D}\) and \(\overline{A C}\) ⊥ \(\overline{C D}\)? Select all that apply.
(A)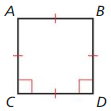
(B)
(C)
(D)
(E)
Answer:

Question 28.
THOUGHT-PROVOKING
The postulates and theorems in this book represent Euclidean geometry. In spherical geometry, all points are points on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere. In spherical geometry. how many right angles are formed by two perpendicular lines? Justify your answer.
Answer:
Given,
The postulates and theorems in this book represent Euclidean geometry. In spherical geometry, all points are points on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere.
In Euclidean geometry, the two perpendicular lines form 4 right angles whereas, In spherical geometry, the two perpendicular lines form 8 right angles according to the Parallel lines Postulate in spherical geometry.
Hence 8 right angles are formed by two perpendicular lines in spherical geometry.

Question 29.
CONSTRUCTION
Construct a square of side length AB

Answer:

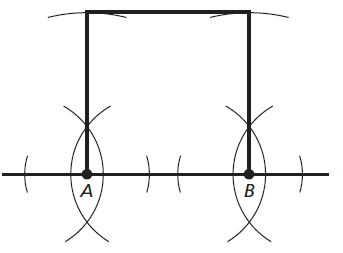
Question 30.
ANALYZING RELATIONSHIPS
The painted line segments that brain the path of a crosswalk are usually perpendicular to the crosswalk. Sketch what the segments in the photo would look like if they were perpendicular to the crosswalk. Which type of line segment requires less paint? Explain your reasoning.

Answer:

Question 31.
ABSTRACT REASONING
Two lines, a and b, are perpendicular to line c. Line d is parallel to line c. The distance between lines a and b is x meters. The distance between lines c and d is y meters. What shape is formed by the intersections of the four lines?
Answer:

Question 32.
MATHEMATICAL CONNECTIONS
Find the distance between the lines with the equations y = \(\frac{3}{2}\) + 4 and – 3x + 2y = – 1.
Answer:
y = \(\frac{3}{2}\) + 4 and -3x + 2y = -1
y = \(\frac{3}{2}\) + 4 and y = \(\frac{3}{2}\)x – \(\frac{1}{2}\)
Compare the given equations with
y = mx + c
m1 = m2 = \(\frac{3}{2}\)
c1 = 4
c2= –\(\frac{1}{2}\)
The distance between the two parallel lines is:
d = | c1 – c2 |
The distance between the given 2 parallel lines = | c1 – c2 |
= | 4 + \(\frac{1}{2}\) |
= \(\frac{9}{2}\)

Question 33.
WRITING
Describe how you would find the distance from a point to a plane. Can you find the distance from a line to a plane? Explain your reasoning.
Answer:

Maintaining Mathematical Proficiency

Simplify the ratio.

Question 34.
\(\frac{6-(-4)}{8-3}\)
Answer:
Given,
\(\frac{6 – (-4)}{8 – 3}\)
= \(\frac{6 + 4}{8 – 3}\)
= \(\frac{10}{5}\)
= 2

Question 35.
\(\frac{3-5}{4-1}\)
Answer:

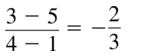
Question 36.
\(\frac{8-(-3)}{7-(-2)}\)
Answer:
Given,
\(\frac{8 – (-3)}{7 – (-2)}\)
= \(\frac{8 + 3}{7 + 2}\)
= \(\frac{11}{9}\)

Question 37.
\(\frac{13-4}{2-(-1)}\)
Answer:

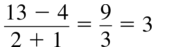
Identify the slope and the y-intercept of the line.

Question 38.
y = 3x + 9
Answer:
y = 3x + 9
y = mx + c
Where,
m is the slope
c is the y-intercept
The slope is: 3
The y-intercept is: 9

Question 39.
y = –\(\frac{1}{2}\)x + 7
Answer:

Question 40.
y = \(\frac{1}{6}\)x – 8
Answer:
y = \(\frac{1}{6}\)x – 8
y = mx + c
m = \(\frac{1}{6}\) and c = -8
The slope is: \(\frac{1}{6}\)
The y-intercept is: -8

Question 41.
y = – 8x – 6
Answer:

3.5 Equations of Parallel and Perpendicular Lines

Exploration 1

Writing Equations of Parallel and Perpendicular Lines

Work with a partner: Write an equation of the line that is parallel or perpendicular to the given line and passes through the given point. Use a graphing calculator to verify your answer. What is the relationship between the slopes?
a.

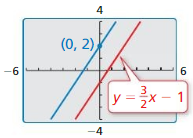
Answer:
The given lines are parallel lines
The equation for another line is:
y = mx + c
y = \(\frac{3}{2}\)x + c
Substitute (0, 2) in the above equation
2 = 0 + c
c = 2
The equation for another parallel line is:
y = \(\frac{3}{2}\)x + 2
The lines that have the same slope and different y-intercepts are Parallel lines.
y = \(\frac{3}{2}\)x – 1
y = \(\frac{3}{2}\)x + 2

b.

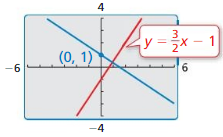
Answer:
The given lines are perpendicular lines
The equation for another line is:
y = \(\frac{3}{2}\)x + c
The slope of perpendicular lines is: -1
m1m2 = -1
\(\frac{3}{2}\) . m2 = -1
m2 = –\(\frac{2}{3}\)
y = –\(\frac{2}{3}\)x + c
Substitute (0, 1) in the above equation
1 = 0 + c
c = 1
The equation for another perpendicular line is:
y = –\(\frac{2}{3}\)x + 1
We can observe that the product of the slopes are -1 and the y-intercepts are different
The lines that have the slopes product -1 and different y-intercepts are Perpendicular lines
y = \(\frac{3}{2}\)x – 1
y = –\(\frac{2}{3}\)x + 1

c.

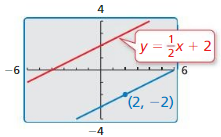
Answer:
The given lines are parallel lines
The equation for another line is:
y = mx + c
y = \(\frac{1}{2}\)x + c
Substitute (2, -2) in the above equation
-2 = \(\frac{1}{2}\) (2) + c
-2 = 1 + c
c = 2 – 1
c = -3
The equation for another parallel line is:
y = \(\frac{1}{2}\)x – 3
When we compare the given equation with the obtained equation
The lines that have the same slope and different y-intercepts are Parallel lines
y = \(\frac{1}{2}\)x + 2
y = \(\frac{1}{2}\)x – 3

d.

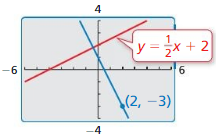
Answer:
From the figure,
The given lines are perpendicular lines
The equation for another line is:
y = \(\frac{1}{2}\)x + c
The slope of perpendicular lines is: -1
m1m2 = -1
\(\frac{1}{2}\) . m2 = -1
m2 = -2
So,
y = -2x + c
Substitute (2, -3) in the equation
-3 = -2 (2) + c
-3 = -4 + c
c = 4 – 3
c = 1
The equation for another perpendicular line is:
y = -2x + 1
We can observe that the product of the slopes are -1 and the y-intercepts are different.
The lines that have the slopes product -1 and different y-intercepts are Perpendicular lines.
y = \(\frac{1}{2}\)x + 2
y = -2x + 1

e.

Answer:
From the figure, the given lines are parallel lines
The equation for another line is:
y = -2x + c
Substitute (0, -2) in the equation
-2 = 0 + c
c = -2
The equation for another parallel line is:
y = -2x – 2
We can observe that the slopes are the same and the y-intercepts are different
The lines that have the same slope and different y-intercepts are Parallel lines
y = -2x + 2
y = -2x – 2

f.

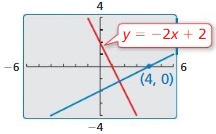
Answer:
From the figure, the given lines are perpendicular lines
The equation for another line is:
y = -2x + c
The slope of perpendicular lines is: -1
m1m2 = -1
-2 . m2 = -1
m2 = \(\frac{1}{2}\)
y = \(\frac{1}{2}\)x + c
Substitute (4, 0) in the equation
0 = \(\frac{1}{2}\) (4) + c
0 = 2 + c
c = 0 – 2
c = -2
The equation for another perpendicular line is:
y = \(\frac{1}{2}\)x – 2
We can observe that the product of the slopes is -1 and the y-intercepts are different
The lines that have the slopes product -1 and different y-intercepts are Perpendicular lines.
y = \(\frac{1}{2}\)x – 2
y = -2x + 2

Exploration 2

Writing Equations of Parallel and Perpendicular Lines

Work with a partner: Write the equations of the parallel or perpendicular lines. Use a graphing calculator to verify your answers.

a.

Answer:
The given lines are the parallel lines
The coordinates of the line of the first equation are: (-1.5, 0), and (0, 3)
The coordinates of the line of the second equation are: (1, 0), and (0, -2)
Compare the given coordinates with
A (x1, y1), and B (x2, y2)
Slope (m) = \(\frac{y2 – y1}{x2 – x1}\)
The slope of the line of the first equation is:
m = \(\frac{3 – 0}{0 + 1.5}\)
m = \(\frac{3}{1.5}\)
m = 2
The standard linear equation is:
y = mx + c
y = 2x + c
The slopes are the same but the y-intercepts are different
The given parallel line equations are:
y = 2x + c1
y = 2x + c2

b.

Answer:
From the figure,
The given lines are perpendicular lines
The coordinates of the line of the first equation are: (0, -3), and (-1.5, 0)
The coordinates of the line of the second equation are: (-4, 0), and (0, 2)
Compare the given coordinates with
A (x1, y1), and B (x2, y2)
Slope (m) = \(\frac{y2 – y1}{x2 – x1}\)
The slope of the line of the first equation is:
m = \(\frac{0 + 3}{0 – 1.5}\)
m = \(\frac{3}{-1.5}\)
m = \(\frac{-30}{15}\)
m = -2
The standard linear equation is:
y = mx + c
y = -2x + c
The product of the slopes is -1 and the y-intercepts are different.
m1 × m2 = -1
-2 × m2 = -1
m2 = \(\frac{1}{2}\)
The given perpendicular line equations are:
y = -2x + c1
y = \(\frac{1}{2}\)x + c2

Communicate Your Answer

Question 3.
How can you write an equation of a line that is parallel or perpendicular to a given line and passes through a given point?
MODELING WITH MATHEMATICS
To be proficient in math, you need to analyze relationships mathematically to draw conclusions.
Answer:
The standard form of a linear equation is:
y = mx + c
The slopes are the same and the y-intercepts are different
To find the y-intercept of the equation that is parallel to the given equation, substitute the given point and find the value of c.
The product of the slopes is -1
The slope of the equation that is perpendicular to the given equation is: –\(\frac{1}{m}\)
To find the y-intercept of the equation that is perpendicular to the given equation, substitute the given point and find the value of c.

Question 4.
Write an equation of the line that is (a) parallel and (b) perpendicular to the line y = 3x + 2 and passes through the point (1, -2).
Answer:
Given,
y = 3x + 2
The given point is: (1, -2)
a) Parallel line equation:
The slope of the parallel equations is the same
The slope of the equation that is parallel t the given equation is: 3
The equation that is parallel to the given equation is
y = 3x + c
Substitute (1, -2) in the equation
-2 = 3 (1) + c
-2 – 3 = c
c = -5
The equation of the line that is parallel to the given equation is y = 3x – 5
b) Perpendicular line equation:
The product of the slope of the perpendicular equations is: -1
m1 m2 = -1
3m2 = -1
m2 = –\(\frac{1}{3}\)
The slope of the equation that is parallel t the given equation is –\(\frac{1}{3}\)
The equation that is perpendicular to the given equation is y = –\(\frac{1}{3}\)x + c
Substitute (1, -2) in the above equation
-2 = –\(\frac{1}{3}\) (-2) + c
-2 – \(\frac{2}{3}\) = c
c = –\(\frac{8}{3}\)
The equation of the line that is perpendicular to the given equation is y = –\(\frac{1}{3}\)x –\(\frac{8}{3}\)

Lesson 3.5 Equations of Parallel and Perpendicular Lines

Monitoring Progress

Find the coordinates of point P along the directed line segment AB so that AP to PB is the given ratio.

Question 1.
A(1, 3), B(8, 4); 4 to 1
Answer:
Given,
A (1, 3), and B (8, 4)
Compare the given points with
A (x1, y1), and B (x2, y2)
AP : PB = 4 : 1
Divide AB into 5 parts
Slope = \(\frac{y2 – y1}{x2 – x1}\)
Slope of AB = \(\frac{4 – 3}{8 – 1}\)
Slope of AB = \(\frac{1}{7}\)
To find the coordinates of P, add slope to AP and PB
P = (4 + (4 / 5) × 7, 1 + (4 / 5) × 1)
P = (22.4, 1.8)
The coordinates of P are (22.4, 1.8)

Question 2.
A(- 2, 1), B(4, 5); 3 to 7
Answer:
Given, A (-2, 1), and B (4, 5)
Compare the given points with
A (x1, y1), and B (x2, y2)
AP : PB = 3 : 7
Divide AB into 10 parts
m = \(\frac{y2 – y1}{x2 – x1}\)
Slope of AB = \(\frac{5 – 1}{4 + 2}\)
Slope of AB = \(\frac{4}{6}\)
Slope of AB = \(\frac{2}{3}\)
To find the coordinates of P, add slope to AP and P
P = (3 + (\(\frac{3}{10}\) × 3), 7 + (\(\frac{3}{10}\) × 2))
P = (3.9, 7.6)
The coordinates of P are (3.9, 7.6)

Question 3.
Determine which of the lines are parallel and which of the lines are perpendicular.

Answer:
From the figure,
The coordinates of line a are (0, 2), and (-2, -2)
The coordinates of line b are (2, 3), and (0, -1)
The coordinates of line c are (4, 2), and (3, -1)
The coordinates of line d are (-3, 0), and (0, -1)
Compare the given coordinates with (x1, y1), and (x2, y2)
The slope of line a (m) = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{-2 – 2}{-2 – 0}\)
= \(\frac{-4}{-2}\)
= 2
The slope of line b (m) = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{-1 – 3}{0 – 2}\)
= \(\frac{-4}{-2}\)
= 2
The slope of line c (m) = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{-1 – 2}{3 – 4}\)
= \(\frac{-3}{-1}\)
= 3
The slope of line d (m) = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{-1 – 0}{0 + 3}\)
= \(\frac{-1}{3}\)
= –\(\frac{1}{3}\)
The parallel lines have the same slopes
The perpendicular lines have the product of slopes equal to -1
Linea and Line b are parallel lines.
Line c and Line d are perpendicular lines.

Question 4.
Write an equation of the line that passes through the point (1, 5) and is
(a) parallel to the line y = 3x – 5 and
Answer:
Given,
y = 3x – 5
(1, 5)
The parallel lines have the same slope
Compare the given equation with
y = mx + c
The slope of the parallel line that passes through (1, 5) is 3
y = 3x + c
To find the value of c, substitute (1, 5) in the above equation
5 = 3 (1) + c
c = 5 – 3
c = 2
The equation of the parallel line that passes through (1, 5) is y = 3x + 2

(b) perpendicular to the line y = 3x – 5.
Answer:
Given,
y = 3x – 5
(1, 5)
The product of the slopes of the perpendicular lines is equal to -1
Compare the given equation with
y = mx + c
m = 3
The slope of the perpendicular line that passes through (1, 5) is m1m2 = -1
3m2 = -1
m2 = –\(\frac{1}{3}\)
The equation of the perpendicular line that passes through (1, 5) is y = –\(\frac{1}{3}\)x + c
To find the value of c, substitute (1, 5) in the above equation
5 = –\(\frac{1}{3}\) + c
c = 5 + \(\frac{1}{3}\)
c = \(\frac{16}{3}\)
The equation of the perpendicular line that passes through (1, 5) is y = –\(\frac{1}{3}\)x + \(\frac{16}{3}\)

Question 5.
How do you know that the lines x = 4 and y = 2 are perpendicular?
Answer:
The given lines are x = 4 and y = 2
The line x = 4 is a vertical line that has the right angle i.e., 90°
The line y = 4 is a horizontal line that has a straight angle i.e., 0°
The angle at the intersection of the 2 lines = 90° – 0° = 90°
The lines x = 4 and y = 2 are perpendicular lines

Question 6.
Find the distance from the point (6, 4) to the line y = x + 4.
Answer:
Given
y = x + 4
Compare the given equation with
ax + by + c = 0
x – y + 4 = 0
a = 1, and b = -1
The distance from the point (6, 4)
The distance from the point (x, y) to the line ax + by + c = 0
d = | ax + by + c| /\(\sqrt{a² + b²}\)
d = | x – y + 4 | / \(\sqrt{1² + (-1)²}\)
d = | x – y + 4 | / \(\sqrt{2}\)}
Substitute (6, 4) in the above equation
So,
d = | 6 – 4 + 4 |/ \(\sqrt{2}\)}
d = 3√2

Question 7.
Find the distance from the point (- 1, 6) to the line y = – 2x.
Answer:
Given,
y = -2x
ax + by + c = 0
2x + y = 0
a = 2, and b = 1
The given point is: (-1, 6)
The distance from the point (x, y) to the line ax + by + c = 0 is
d = | ax + by + c| /\(\sqrt{a² + b²}\)
d = | 2x + y | / \(\sqrt{2² + (1)²}\)
d = | 2x + y | / \(\sqrt{5}\)}
Substitute (-1, 6) in the above equation
So,
d = | -2 + 6 |/ \(\sqrt{5}\)
d = \(\frac{4}{√5}\)

Exercise 3.5 Equations of Parallel and Perpendicular Lines

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
A _________ line segment AB is a segment that represents moving from point A to point B.
Answer:
A directed line segment AB is a segment that represents moving from point A to point B.

Question 2.
WRITING
How are the slopes of perpendicular lines related?
Answer:
The Perpendicular lines are lines that intersect at right angles.
If you multiply the slopes of two perpendicular lines in the plane, you get −1 i.e., the slopes of perpendicular lines are opposite reciprocals.

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 6. find the coordinates of point P along the directed line segment AB so that AP to PB is the given ratio.

Question 3.
A(8, 0), B(3, – 2); 1 to 4
Answer:

Question 4.
A(- 2, – 4), B(6, 1); 3 to 2
Answer:
A (-2, -4), and B (6, 1)
Compare the given points with
A (x1, y1), and B (x2, y2)
AP : PB = 3 : 2
Divide AB into 5 parts
Slope (m) = \(\frac{y2 – y1}{x2 – x1}\)
Slope of AB = \(\frac{1 + 4}{6 + 2}\)
Slope of AB = \(\frac{5}{8}\)
To find the coordinates of P, add slope to AP and PB
So,
P = (3 + (3 / 5) × 8, 2 + (3 / 5) × 5)
P = (7.8, 5)
The coordinates of P are (7.8, 5)

Question 5.
A(1, 6), B(- 2, – 3); 5 to 1
Answer:

Question 6.
A(- 3, 2), B(5, – 4); 2 to 6
Answer:
Given,
A (-3, 2), and B (5, -4)
Compare the given points with
A (x1, y1), and B (x2, y2)
AP : PB = 2 : 6
Divide AB into 8 parts
Slope (m) = \(\frac{y2 – y1}{x2 – x1}\)
Slope of AB = \(\frac{-4 – 2}{5 + 3}\)
Slope of AB = \(\frac{-6}{8}\)
To find the coordinates of P, add slope to AP and PB
P = (2 + (2 / 8) × 8, 6 + (2 / 8) × (-6))
P = (4, 4.5)
The coordinates of P are (4, 4.5)

In Exercises 7 and 8, determine which of the lines are parallel and which of the lines are perpendicular.

Question 7.

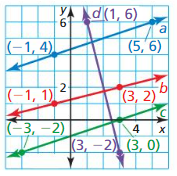
Answer:

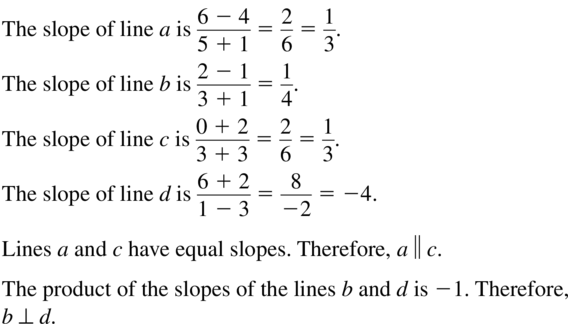
Question 8.

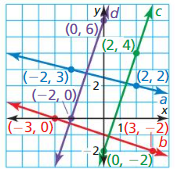
Answer:
From the figure,
The coordinates of line a are (2, 2), and (-2, 3)
The coordinates of line b are (3, -2), and (-3, 0)
The coordinates of line c are (2, 4), and (0, -2)
The coordinates of line d are (0, 6), and (-2, 0)
Compare the given coordinates with (x1, y1), and (x2, y2)
The slope of line a (m) = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{3 – 2}{-2 – 2}\)
= \(\frac{1}{-4}\)
= –\(\frac{1}{4}\)
The slope of line b (m) = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{0 + 2}{-3 – 3}\)
= \(\frac{2}{-6}\)
= –\(\frac{1}{3}\)
The slope of line c (m) = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{-4 – 2}{0 – 2}\)
= \(\frac{-6}{-2}\)
= 3
The slope of line d (m) = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{6 – 0}{0 + 2}\)
= \(\frac{6}{2}\)
= 3
The parallel lines have the same slopes
The perpendicular lines have the product of slopes equal to -1.
Line c and Line d are parallel lines
Line b and Line c are perpendicular lines

In Exercises 9 – 12, tell whether the lines through the given points are parallel, perpendicular, or neither. justify your answer.

Question 9.
Line 1: (1, 0), (7, 4)
Line 2: (7, 0), (3, 6)
Answer:

Question 10.
Line 1: (- 3, 1), (- 7, – 2)
Line 2: (2, – 1), (8, 4)
Answer:
The coordinates of line 1 are (-3, 1), (-7, -2)
The coordinates of line 2 are (2, -1), (8, 4)
Compare the given coordinates with
(x1, y1), (x2, y2)
Slope (m) = \(\frac{y2 – y1}{x2 – x1}\)
Slope of line 1 = \(\frac{-2 – 1}{-7 + 3}\)
= \(\frac{-3}{-4}\)
= \(\frac{3}{4}\)
Slope of line 2 = \(\frac{4 + 1}{8 – 2}\)
= \(\frac{5}{6}\)
By comparing the slopes, we can say that the given lines are neither parallel nor perpendicular

Question 11.
Line 1: (- 9, 3), (- 5, 7)
Line 2: (- 11, 6), (- 7, 2)
Answer:

Question 12.
Line 1: (10, 5), (- 8, 9)
Line 2: (2, – 4), (11, – 6)
Answer:
The coordinates of line 1 are (10, 5), (-8, 9)
The coordinates of line 2 are (2, -4), (11, -6)
Compare the given coordinates with
(x1, y1), (x2, y2)
Slope (m) = \(\frac{y2 – y1}{x2 – x1}\)
Slope of line 1 = \(\frac{9 – 5}{-8 – 10}\)
= \(\frac{4}{-18}\)
= –\(\frac{2}{9}\)
Slope of line 2 = \(\frac{4 – 6}{11 – 2}\)
= \(\frac{-2}{9}\)
= –\(\frac{2}{9}\)
The given lines are parallel

In Exercises 13 – 16. write an equation of the line passing through point P that ¡s parallel to the given line. Graph the equations of the lines to check that they are parallel.

Question 13.
P(0, – 1), y = – 2x + 3
Answer:

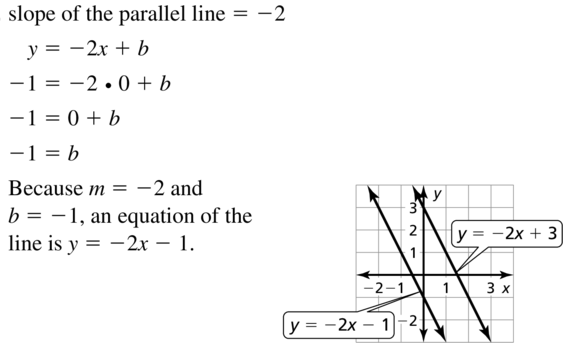
Question 14.
P(3, 8), y = \(\frac{1}{5}\)(x + 4)
Answer:
Given,
y = \(\frac{1}{5}\) (x + 4)
P (3, 8)
y = \(\frac{1}{5}\)x + \(\frac{4}{5}\)
The slopes are equal fot the parallel lines
The equation that is parallel to the given equation is y = \(\frac{1}{5}\)x + c
Substitute P (3, 8) in the above equation to find the value of c
8 = \(\frac{1}{5}\) (3) + c
c = 8 – \(\frac{3}{5}\)
c = \(\frac{37}{5}\)
The parallel line equation that is parallel to the given equation is y = \(\frac{1}{5}\)x + \(\frac{37}{5}\)

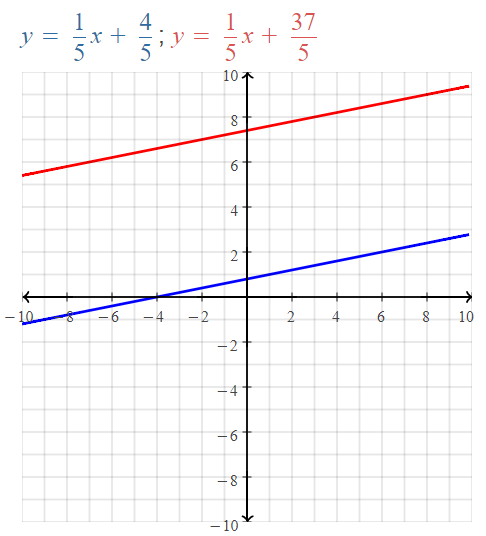
Question 15.
P(- 2, 6), x = – 5
Answer:

Question 16.
P(4, 0), – x + 2y = 12
Answer:
Given,
-x + 2y = 12
The given point is: P (4, 0)
y = \(\frac{1}{2}\)x + 6
The slopes are equal fot the parallel lines
The equation that is parallel to the given equation is y = \(\frac{1}{2}\)x + c
Substitute P (4, 0) in the above equation to find the value of c
0 = \(\frac{1}{2}\) (4) + c
c = 2 – 0
c = 2
The parallel line equation that is parallel to the given equation is y = \(\frac{1}{2}\)x + 2

In Exercises 17 – 20. write an equation of the line passing through point P that is perpendicular to the given line. Graph the equations of the lines to check that they are perpendicular.

Question 17.
P(0, 0), y = – 9x – 1
Answer:

Question 18.
P(4, – 6); y = – 3
Answer:
Given,
y = -3; P (4, -6)
The line that is perpendicular to y=n is
x = n
The line that is perpendicular to the given equation is:
x = n
Substitute P (4, -6) in the equation
x = 4
The equation that is perpendicular to y = -3 is:
x = 4

Question 19.
P(2, 3), y – 4 = – 2(x + 3)
Answer:

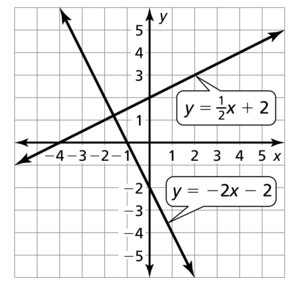
Question 20.
P(- 8, 0), 3x – 5y = 6
Answer:
Given,
3x – 5y = 6
P (-8, 0)
5y = 3x – 6
y = \(\frac{3}{5}\)x – \(\frac{6}{5}\)
The product of the slopes of perpendicular lines is equal to -1
m = –\(\frac{5}{3}\)
The equation that is perpendicular to the given line equation is y = –\(\frac{5}{3}\)x + c
Substitute P(-8, 0) in the above equation
0 = –\(\frac{5}{3}\) ( -8) + c
c = \(\frac{40}{3}\)
The equation that is perpendicular to the given equation is y = –\(\frac{5}{3}\)x + \(\frac{40}{3}\)

In Exercises 21 – 24, find the distance from point A to the given line.

Question 21.
A(- 1, 7), y = 3x
Answer:

Question 22.
A(- 9, – 3), y = x – 6
Answer:
Given,
y = x – 6; A (-9, -3)
Compare the given equation with
y = mx + c
The product of the slopes of the perpendicular lines is equal to -1
m1m2 = -1
1 (m2) = -3
m2 = -1
The equation that is perpendicular to the given line equation is y = -x + c
To find c:
-3 = 9 + c
c = -9 – 3
c = -12
The equation that is perpendicular to the given line equation is y = -x – 12
Solve 1 & 2,
x – 6 = -x – 12
x + x = -12 + 6
2x = -6
x = \(\frac{-6}{2}\)
x = -3
y = x – 6
y = -3 – 6
y = -9
The point of intersection = (-3, -9)
The points are: (-9, -3), (-3, -9)
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(9 – 3)² + (9 – 3)²}\)
= \(\sqrt{(6)² + (6)²}\)
= 8.48

Question 23.
A(15, – 21), 5x + 2y = 4
Answer:

Question 24.
A(- \(\frac{1}{4}\), 5), – x + 2y = 14
Answer:
-x + 2y = 14
y = \(\frac{1}{2}\)x + 7
A (-\(\frac{1}{4}\), 5)
Compare the given equation with
y = mx + c
The product of the slopes of the perpendicular lines is equal to -1
m1m2 = -1
\(\frac{1}{2}\) (m2) = -1
m2 = -2
The equation that is perpendicular to the given line equation is
y = -2x + c
To find c:
5 = -2 (-\(\frac{1}{4}\)) + c
c = 5 – \(\frac{1}{2}\)
c = \(\frac{9}{2}\)
The equation that is perpendicular to the given line equation is
y = -2x + \(\frac{9}{2}\)
Solve 1 & 2
\(\frac{1}{2}\)x + 7 = -2x + \(\frac{9}{2}\)
\(\frac{1}{2}\)x + 2x = -7 + 9/2
\(\frac{5}{2}\)x = –\(\frac{5}{2}\)
x = -1
y = -2x + 3
y = -2 (-1) + \(\frac{9}{2}\)
y = \(\frac{13}{2}\)
The point of intersection = (-1, \(\frac{13}{2}\))
The points are: (-\(\frac{1}{4}\), 5), (-1, \(\frac{13}{2}\))
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 / 2)² + (3 / 4)²}\)
= 1.67

Question 25.
ERROR ANALYSIS
Describe and correct the error in determining whether the lines are parallel. perpendicular, or neither.

Answer:

Question 26.
ERROR ANALYSIS
Describe and correct the error in writing an equation of the line that passes through the point (3, 4) and is parallel to the line y = 2x + 1.

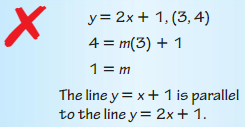
Answer:
y = 2x + 1
(3, 4)
The slopes of the parallel lines are the same
Compare the given equation with
y = mx + c
m = 2
The slope of the line that is parallel to the given line equation is
m = 2
The equation of the line that is parallel to the given equation is:
y = 2x + c
To find c:
Substitute (3, 4) in the equation
4 = 2 (3) + c
4 – 6 = c
c = -2
y = 2x – 2

In Exercises 27-30. find the midpoint of \(\overline{P Q}\). Then write
an equation of the line that passes through the midpoint and is perpendicular to \(\overline{P Q}\). This line is called the perpendicular bisector.

Question 27.
P( – 4, 3), Q(4, – 1)
Answer:

Question 28.
P(- 5, – 5), Q(3, 3)
Answer:
Given,
P (-5, -5), Q (3, 3)
Compare the given points with (x1, y1), (x2, y2)
The midpoint of PQ = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
= (\(\frac{-5 + 3}{2}\), \(\frac{-5 + 3}{2}\))
= (\(\frac{-2}{2}\), \(\frac{-2}{2}\))
= (-1, -1)
The slope of PQ = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{3 + 5}{3 + 5}\)
= \(\frac{8}{8}\)
= 1
The product of the slopes of the perpendicular lines is equal to -1
m1m2 = -1
m2 = -1
The equation of the perpendicular line that passes through the midpoint of PQ
y = -x + c
To find c:
Substitute (-1, -1) in the equation
-1 = -1 + c
c = 0
The equation of the line that is perpendicular bisector is:
y = -x

Question 29.
P(0, 2), Q(6, – 2)
Answer:

Question 30.
P(- 7, 0), Q(1, 8)
Answer:
Given,
P (-7, 0), Q (1, 8)
Compare the given points with (x1, y1), (x2, y2)
The midpoint of PQ = (\(\frac{x1 + x2}{2}\), \(\frac{y1 + y2}{2}\))
= (\(\frac{8 + 0}{2}\), \(\frac{-7 + 1}{2}\))
= (\(\frac{8}{2}\), \(\frac{-6}{2}\))
= (4, -3)
The slope of PQ = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{8 – 0}{1 + 7}\)
= \(\frac{8}{8}\)
= 1
The product of the slopes of the perpendicular lines is equal to -1
m1m2 = -1
m2 = -1
The equation of the perpendicular line that passes through the midpoint of PQ is
y = -x + c
To find c:
Substitute (4, -3) in the equation
-3 = -4 + c
c = -3 + 4
c = 1
The equation of the line that is perpendicular bisector is y = -x + 1

Question 31.
MODELING WITH MATHEMATICS
Your school lies directly between your house and the movie theater. The distance from your house to the school is one-fourth of the distance from the school to the movie theater. What point on the graph represents your school?

Answer:

Question 32.
REASONING
Is quadrilateral QRST a parallelogram? Explain your reasoning.

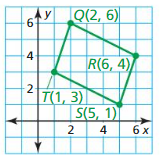
Answer:
From the figure,
The coordinates of the quadrilateral QRST is:
Q (2, 6), R (6, 4), S (5, 1), and T (1, 3)
Compare the given points with (x1, y1), and (x2, y2)
If both pairs of opposite sides of a quadrilateral are parallel, then it is a parallelogram
If the slopes of the opposite sides of the quadrilateral are equal, then it is called a Parallelogram
Slope (m) = \(\frac{y2 – y1}{x2 – x1}\)
Slope of QR = \(\frac{4 – 6}{6 – 2}\)
Slope of QR = \(\frac{-2}{4}\)
Slope of QR = –\(\frac{1}{2}\)

Slope of RS = \(\frac{1 – 4}{5 – 6}\)
Slope of RS = \(\frac{-3}{-1}\)
Slope of RS = 3

Slope of ST = \(\frac{3 – 1}{1 – 5}\)
Slope of ST = \(\frac{2}{-4}\)
Slope of ST = –\(\frac{1}{2}\)

Slope of TQ = \(\frac{3 – 6}{1 – 2}\)
Slope of TQ = \(\frac{-3}{-1}\)
Slope of TQ = 3
We can observe that the slopes of the opposite sides are equal i.e., the opposite sides are parallel
Quadrilateral QRST is a parallelogram.

Question 33.
REASONING
A triangle has vertices L(0, 6), M(5, 8). and N(4, – 1), Is the triangle a right triangle? Explain ‘your reasoning.
Answer:

Question 34.
MODELING WITH MATHEMATICS
A new road is being constructed parallel to the train tracks through points V. An equation of the line representing the train tracks is y = 2x. Find an equation of the line representing the new road.

Answer:
It is given that a new road is being constructed parallel to the train tracks through points V. An equation of the line representing the train tracks is y = 2x
V = (-2, 3)
The slopes of the parallel lines are the same
By comparing the given equation with
y = mx + c
m = 2
y = 2x + c
To find c:
Substitute (-2, 3) in the equation
3 = 2 (-2) + x
3 + 4 = c
c = 7
The equation of the line that is parallel to the line representing railway tracks is y = 2x + 7

Question 35.
MODELING WITH MATHEMATICS
A bike path is being constructed perpendicular to Washington Boulevard through point P(2, 2). An equation of the line representing Washington Boulevard is y = –\(\frac{2}{3}\)x. Find an equation of the line representing the bike path.

Answer:

Question 36.
PROBLEM-SOLVING
A gazebo is being built near a nature trail. An equation of the line representing the nature trail is y = \(\frac{1}{3}\)x – 4. Each unit in the coordinate plane corresponds to 10 feet. Approximately how far is the gazebo from the nature trail?

Answer:
Given,
A gazebo is being built near a nature trail. An equation of the line representing the nature trail is y = \(\frac{1}{3}\)x – 4.
Each unit in the coordinate plane corresponds to 10 feet.
1 unit either in the x-plane or y-plane = 10 feet
y = \(\frac{1}{3}\)x – 4
y = \(\frac{1}{3}\) (10) – 4
y = \(\frac{10 – 12}{3}\)
y = –\(\frac{2}{3}\)
The distance won’t be in a negative value,
y = \(\frac{2}{3}\)
y = 0.66 feet

Question 37.
CRITICAL THINKING
The slope of line l is greater than 0 and less than 1. Write an inequality for the slope of a line perpendicular to l. Explain your reasoning.
Answer:

Question 38.
HOW DO YOU SEE IT?
Determine whether quadrilateral JKLM is a square. Explain your reasoning.

Answer:
From the figure
The coordinates of a quadrilateral are J (0 0), K (0, n), L (n, n), M (n, 0)
Compare the given points with (x1, y1), and (x2, y2)
Slope (m) = \(\frac{y2 – y1}{x2 – x1}\)
Slope of JK = \(\frac{n – 0}{0 – 0}\) = Undefined
Slope of KL = \(\frac{n – n}{n – 0}\) = 0
Slope of LM = \(\frac{0 – n}{n – n}\) = Undefined
Slope of MJ = \(\frac{0 – 0}{n – 0}\) = 0
The slopes of perpendicular lines are undefined and 0 respectively
Quadrilateral JKLM is a square.

Question 39.
CRITICAL THINKING
Suppose point P divides the directed line segment XY So that the ratio 0f XP to PY is 3 to 5. Describe the point that divides the directed line segment YX so that the ratio of YP Lo PX is 5 to 3.
Answer:

Question 40.
MAKING AN ARGUMENT
Your classmate claims that no two nonvertical parallel lines can have the same y-intercept. Is your classmate correct? Explain.
Answer:
It is given that your classmate claims that no two nonvertical parallel lines can have the same y-intercept.
The parallel lines have the same slope but have different y-intercepts and do not intersect.
The intersecting lines intersect each other and have different slopes and have the same y-intercept.
Your classmate is correct

Question 41.
MATHEMATICAL CONNECTIONS
Solve each system of equations algebraically. Make a conjecture about what the solution(s) can tell you about whether the lines intersect. are parallel, or are the same line.
a. y = 4x + 9
4x – y = 1
b. 3y + 4x = 16
2x – y = 18
c. y = – 5x + 6
10x + 2y = 12
Answer:

Question 42.
THOUGHT-PROVOKING
Find a formula for the distance from the point (x_{0, Y0}) to the line ax + by = 0. Verify your formula using a point and a line.
Answer:





MATHEMATICAL CONNECTIONS
In Exercises 43 and 44, find a value for k based on the given description.

Question 43.
The line through (- 1, k) and (- 7, – 2) is parallel to the line y = x + 1.
Answer:

Question 44.
The line through (k, 2) and (7, 0) is perpendicular to the line y = x – \(\frac{28}{5}\).
Answer:
The line through (k, 2) and (7, 0) is perpendicular to the line y = x – \(\frac{28}{5}\)
The given line that is perpendicular to the given points is y = x – \(\frac{28}{5}\)
Compare the given points with (x1, y1), and (x2, y2)
Slope (m) = \(\frac{y2 – y1}{x2 – x1}\)
m = \(\frac{0 – 2}{7 – k}\)
m = \(\frac{-2}{7 – k}\)
The slope that is perpendicular to the given line is
m = -1 [ Since we know that m1m2 = -1]
-1 = \(\frac{-2}{7 – k}\)
k – 7 = -2
k = -2 + 7
k = 5

Question 45.
ABSTRACT REASONING
Make a conjecture about how to find the coordinates of a point that lies beyond point B along \(\vec{A}\)B. Use an example to support your conjecture.
Answer:

Question 46.
PROBLEM-SOLVING
What is the distance between the lines y = 2x and y = 2x + 5? Verify your answer.
Answer:
Given,
y = 2x and y = 2x + 5
Compare the given equations with
y = mx + c
To find the distance between the two lines, we have to find the intersection point of the line.
The intersection of the line is the y-intercept.
y = 2x + 5,
The intersection point is (0, 5)
Find the perpendicular line of y = 2x and find the intersection point of the two lines
The product of the slopes of the perpendicular lines is equal to -1
m1 . m2 = -1
2m2 = -1
m2 = –\(\frac{1}{2}\)
The perpendicular equation of y = 2x is
y = –\(\frac{1}{2}\)x + c
To find the value of c in the above equation, substitute (0, 5) in the above equation.
5 = c
c = 5
The perpendicular line equation of y = 2x is:
y = –\(\frac{1}{2}\)x + 5
For the intersection point,
2x = –\(\frac{1}{2}\)x + 5
2x + \(\frac{1}{2}\)x = 5
\(\frac{5}{2}\)x = 5
x = 2
y = 2x
= 2 (2)
= 4
The intersection point of y = 2x is: (2, 4)
The points are: (0, 5), and (2, 4)
Compare the given points with (x1, y1), and (x2, y2)
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(4 – 5)² + (2 – 0)²}\)
= \(\sqrt{1 + 4}\)
d = 2.23

PROVING A THEOREM
In Exercises 47 and 48, use the slopes of lines to write a paragraph proof of the theorem.

Question 47.
Lines Perpendicular to a Transversal Theorem (Theorem 3.12): In a plane. if two lines are perpendicular to the same line. then they are parallel to each other.
Answer:

Question 48.
Transitive Property of Parallel Lines Theorem (Theorem 3.9): If two lines are parallel to the same line, then they are parallel to each other.
Answer:
If two lines are parallel to the same line, then they are parallel to each other
Proof:
Let the two parallel lines be E and F and the plane they lie be plane x.
Let the two parallel lines that are parallel to the same line be G.
According to the Transitive Property of parallel lines,
If line E is parallel to line F and line F is parallel to line G, then line E is parallel to line G.

Question 49.
PROOF
Prove the statement: If two lines are vertical. then they are parallel.
Answer:

Question 50.
PROOF
Prove the statement: If two lines are horizontal, then they are parallel.
Answer:
If two lines are horizontal, then they are parallel
Proof:
If two lines x and y are horizontal lines and they are cut by a vertical transversal z, then
x ⊥ z and y ⊥ z
x || y is proved by the Lines parallel to Transversal Theorem

Question 51.
PROOF
Prove that horizontal lines are perpendicular to vertical lines.
Answer:

Maintaining Mathematical Proficiency

Plot the point in a coordinate plane.

Question 52.
A(3, 6)
Answer:
A(3, 6)
The representation of the given point in the coordinate plane is:

Question 53.
B(0, – 4)
Answer:

Question 54.
C(5, 0)
Answer:
C (5, 0)
The representation of the given point in the coordinate plane is:

Question 55.
D( – 1, – 2)
Answer:

Copy and complete the table.

Question 56.

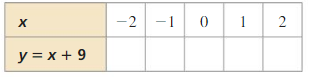
Answer:
The given table is:

From the above table,
The given equation is:
y = x + 9
The completed table is:

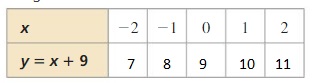
Question 57.

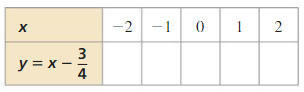
Answer:

3.4 – 3.5 Performance Task: Navajo Rugs

Mathematical Practices

Question 1.
Compare the effectiveness of the argument in Exercise 24 on page 153 with the argument “You can find the distance between any two parallel lines” What flaw(s) exist in the argument(s)? Does either argument use correct reasoning? Explain.
Answer:
The claim of your friend is not correct
If we want to find the distance from the point to a given line, we need the perpendicular distance of a point and a line
We can not find the distance between any two parallel lines if a point and a line are given to find the distance.

Question 2.
Look back at your construction of a square in Exercise 29 on page 154. How would your
construction change if you were to construct a rectangle?
Answer:
The length of all the line segments is equal
If you were to construct a rectangle.
We have to keep the lengths of the length of rectangles the same and the widths of the rectangle also the same.

Question 3.
In Exercise 31 on page 161, a classmate tells you that our answer is incorrect because you should have divided the segment into four congruent pieces. Respond to your classmates’ argument by justifying your original answer.
Answer:
We divided the total distance into the four congruent segments or pieces
We can conclude that the argument of your friend that the answer is incorrect is not correct.

Parallel and Perpendicular Lines Chapter Review

3.1 Pairs of Lines and Angles

Think of each segment in the figure as part of a line. Which line(s) or plane(s) appear to fit the description?

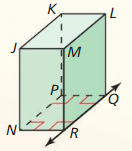
Question 1.
line(s) perpendicular to
Answer:
The lines that are at 90° are Perpendicular lines.
From the figure,
The lines perpendicular to \(\overline{Q R}\) are \(\overline{R M}\) and \(\overline{Q L}\)

Question 2.
line(s) parallel to
Answer:
The lines that do not have any intersection points are called Parallel lines.
From the figure,
The line parallel to \(\overline{Q R}\) is \(\overline {L M}\)

Question 3.
line(s) skew to
Answer:
The lines that do not intersect and are not parallel and are not coplanar are Skew lines.
From the figure,
The lines skew to \(\overline{Q R}\) are \(\overline{J N}\), \(\overline{J K}\), \(\overline{K L}\), and \(\overline{L M}\)

Question 4.
plane(s) parallel to plane LMQ
Answer:
From the figure,
We can conclude that the plane parallel to plane LMQ is Plane JKL

3.2 Parallel Lines and Transversals

Find the values of x and y.

Question 5.

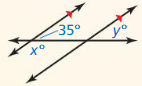
Answer:
From the figure,
We can observe that x and 35° are the corresponding angles
By using the Corresponding Angles Theorem,
x = 35°
x + y = 180
35° + y = 180°
y = 180° – 35°
y = 145°

Question 6.

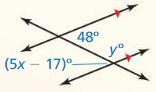
Answer:
From the figure,
We can observe that 48° and y are the consecutive interior angles and y and (5x – 17)° are the corresponding angles
So,
By using the Consecutive Interior Angles Theorem,
48° + y° = 180°
y° = 180° – 48°
y° = 132°
y° = (5x – 17)°
132° = (5x – 17)°
5x = 132° + 17°
5x = 149°
x = \(\frac{149}{5}\)
x° = 29.8°

Question 7.

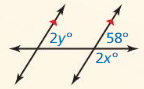
Answer:
From the figure,
2x° and 2y° are the alternate exterior angles
2y° and 58° are the alternate interior angles
2x° = 2y° = 58°
x° = y° = 58/2
x° = y° =29°

Question 8.

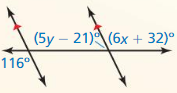
Answer:
From the figure,
(5y – 21)° and 116° are the corresponding angles
(5y – 21)° = 116°
5y° = 116° + 21°
5y° = 137°
y° = \(\frac{137}{5}\)
y° = 27.4°
(5y – 21)° ad (6x + 32)° are the alternate interior angles
(5y – 21)° = (6x + 32)°
5 (28)° – 21° = (6x + 32)°
140 – 21 – 32 = 6x°
6x° = 140° – 53°
6x = 87°
x = \(\frac{87}{6}\)
x° = 14.5°

3.3 Proofs with Parallel Lines

Find the value of x that makes m || n.

Question 9.

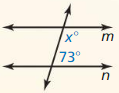
Answer:
m || n is true only when x and 73° are the consecutive interior angles according to the Converse of Consecutive Interior angles Theorem.
It is given that m || n
x + 73° = 180°
x = 180° – 73°
x = 107°

Question 10.

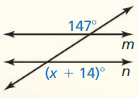
Answer:
m || n is true only when 147° and (x + 14)° are the corresponding angles by using the Converse of the Alternate Exterior Angles Theorem
It is given that m || n
So,
(x + 14)°= 147°
x° = 147° – 14°
x° = 133°

Question 11.

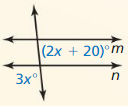
Answer:
m || n is true only when 3x° and (2x + 20)° are the corresponding angles by using the Converse of the Corresponding Angles Theorem
It is given that m || n
(2x + 20)°= 3x°
3x° – 2x° = 20°
x° = 20°

Question 12.

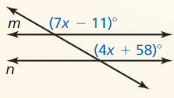
Answer:
m || n is true only when (7x – 11)° and (4x + 58)° are the alternate interior angles by the Converse of the Consecutive Interior Angles Theorem
It is given that m || n
(7x – 11)° = (4x + 58)°
7x° – 4x° = 58° + 11°
3x° = 69°
x° = \(\frac{69}{3}\)
x° = 23°

3.4 Proofs with Perpendicular Lines

Determine which lines, if any, must be parallel. Explain your reasoning.

Question 13.

Answer:
From the figure,
x ⊥ z and y ⊥ z
According to the Perpendicular Transversal Theorem,
In a plane, if a line is perpendicular to one of two parallel lines, then it is perpendicular to the other line also.
We can say that x and y are parallel lines.

Question 14.

Answer:
From the figure,
We can observe that
w ⊥ y and z ⊥ x
We can also observe that w and z is not both ⊥ to x and y
According to the Perpendicular Transversal Theorem,
In a plane, if a line is perpendicular to one of two parallel lines, then it is perpendicular to the other line also.
We can say that there are not any parallel lines in the given figure.

Question 15.

Answer:
From the figure,
m ⊥ a, n ⊥ a, l ⊥ b, and n ⊥ b
According to the Perpendicular Transversal Theorem,
In a plane, if a line is perpendicular to one of two parallel lines, then it is perpendicular to the other line also.
We can say that m and n are parallel lines

Question 16.

Answer:
From the figure,
a ⊥ n, b ⊥ n, and c ⊥ m
According to the Perpendicular Transversal Theorem,
In a plane, if a line is perpendicular to one of two parallel lines, then it is perpendicular to the other line also.
We can say that there are not any parallel lines in the given figure.

3.5 Equations of Parallel and Perpendicular Lines

Write an equation of the line passing through the given point that is parallel to the given line.

Question 17.
A(3, – 4),y = – x + 8
Answer:
Given,
y = -x + 8
A (3, -4)
The slopes are equal for the parallel lines.
The equation that is parallel to the given equation is y = -x + c
To find c:
-4 = -3 + c
c = -4 + 3
c = -1
The parallel line equation that is parallel to the given equation is y = -x – 1

Question 18.
A(- 6, 5), y = \(\frac{1}{2}\)x – 7
Answer:
Given,
y = \(\frac{1}{2}\)x – 7
A (-6, 5)
The slopes are equal for the parallel lines
The equation that is parallel to the given equation is y = \(\frac{1}{2}\)x + c
5 = \(\frac{1}{2}\) (-6) + c
c = 5 + 3
c = 8
The parallel line equation that is parallel to the given equation is y = \(\frac{1}{2}\)x + 8

Question 19.
A(2, 0), y = 3x – 5
Answer:
y = 3x – 5
A (2, 0)
The slopes are equal for the parallel lines
The equation that is parallel to the given equation is y = 3x + c
To find c:
0 = 3 (2) + c
c = 6 – 0
c = 6
The parallel line equation that is parallel to the given equation is y = 3x – 6

Question 20.
A(3, – 1), y = \(\frac{1}{3}\)x + 10
Answer:
Given,
A (3, -1)
y = \(\frac{1}{3}\)x + 10
The slopes are equal for the parallel lines
The equation that is parallel to the given equation is y = \(\frac{1}{3}\)x + c
-1 = \(\frac{1}{3}\) (3) + c
c = -1 – 1
c = -2
The parallel line equation that is parallel to the given equation is y = \(\frac{1}{3}\)x – 2

Write an equation of the line passing through the given point that is perpendicular to the given line.

Question 21.
A(6, – 1), y = – 2x + 8
Answer:
Given,
y = -2x + 8
A (6, -1)
The product of the slopes of perpendicular lines is equal to -1
m = \(\frac{1}{2}\)
The equation that is perpendicular to the given line equation is y = \(\frac{1}{2}\)x + c
-1 = \(\frac{1}{2}\) ( 6) + c
c = -1 – 3
c = -4
The equation that is perpendicular to the given equation is y = \(\frac{1}{2}\)x – 4

Question 22.
A(0, 3), y = – \(\frac{1}{2}\)x – 6
Answer:
Given,
y = –\(\frac{1}{2}\)x – 6
A (0, 3)
The product of the slopes of perpendicular lines is equal to -1
m = 2
The equation that is perpendicular to the given line equation is y = 2x + c
3 = 2 ( 0) + c
c = 3
The equation that is perpendicular to the given equation is y = 2x + 3

Question 23.
A(8, 2),y = 4x – 7
Answer:
Given,
y = 4x – 7
A (8, 2)
The product of the slopes of perpendicular lines is equal to -1
m = –\(\frac{1}{4}\)
The equation that is perpendicular to the given line equation is y = –\(\frac{1}{4}\)x + c
2 = –\(\frac{1}{4}\) (8) + c
c = 2 + 2
c = 4
The equation that is perpendicular to the given equation is y = –\(\frac{1}{4}\)x + 4

Question 24.
A(-1, 5), y = \(\frac{1}{7}\)x + 4
Answer:
Given,
y = \(\frac{1}{7}\)x + 4
A (-1, 5)
The product of the slopes of perpendicular lines is equal to -1
m = -7
The equation that is perpendicular to the given line equation is y = -7x + c
5 = -7 ( -1) + c
c = 5 – 7
c = -2
The equation that is perpendicular to the given equation is y = -7x – 2

Find the distance front point A to the given line.

Question 25.
A(2, – 1), y = – x + 4
Answer:
Given,
y = -x + 4 and A (2, -1)
y = mx + c
The product of the slopes of the perpendicular lines is equal to -1
m1m2 = -1
(-1) (m2) = -1
m2 = 1
The equation that is perpendicular to the given line equation is y = x + c
-1 = 2 + c
c = -1 – 2
c = -3
The equation that is perpendicular to the given line equation is y = x – 3
Solving 1 & 2 equations
-x + 4 = x – 3
-x – x = -3 – 4
2x = 7
x = \(\frac{7}{2}\)
y = x – 3
y = \(\frac{7}{2}\) – 3
y = \(\frac{1}{2}\)
The point of intersection = (\(\frac{7}{2}\), \(\frac{1}{2}\))
The points are: (2, -1), (\(\frac{7}{2}\), \(\frac{1}{2}\))
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(3 / 2)² + (3 / 2)²}\)
= 2.12

Question 26.
A(- 2, 3), y = \(\frac{1}{2}\)x + 1
Answer:
Given,
y = \(\frac{1}{2}\)x + 1
The given point is: A (-2, 3)
y = mx + c
The product of the slopes of the perpendicular lines is equal to -1
m1m2 = -1
(\(\frac{1}{2}\)) (m2) = -1
m2 = -2
The equation that is perpendicular to the given line equation is y = -2x + c
3 = -2 (-2) + c
c = 3 – 4
c = -1
The equation that is perpendicular to the given line equation is y = -2x – 1
Solving 1 & 2 equations
\(\frac{1}{2}\)x + 1 = -2x – 1
\(\frac{5}{2}\)x = 2
x = \(\frac{4}{5}\)
y = -2x – 1
y = –\(\frac{8}{5}\) – 1
y = –\(\frac{13}{5}\)
The point of intersection = (\(\frac{4}{5}\), –\(\frac{13}{5}\))
The points are (-2, 3), (\(\frac{4}{5}\), –\(\frac{13}{5}\))
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{31.36 + 7.84}\)
= 6.26

Parallel and Perpendicular Lines Test

Find the values of x and y. State which theorem(s) you used.

Question 1.

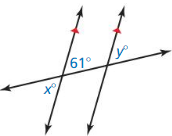
Answer:
From the figure,
x and 61° are the vertical angles
61° and y° are the alternate interior angles
x° = y° = 61°

Question 2.

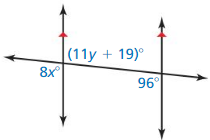
Answer:
From the figure,
8x° and 96° are the alternate interior angles
(11y + 19)° and 96° are the corresponding angles
8x° = 96°
x° = \(\frac{96}{8}\)
x° = 12°
(11y + 19)° = 96°
11y° = 96° – 19°
11y° = 77°
y° = \(\frac{77}{11}\)
y° = 7°
So, x° = 12° and y° = 7°

Question 3.

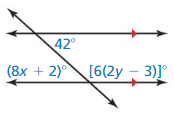
Answer:
From the figure,
42° and 6(2y – 3)° are the consecutive interior angles
42° and (8x + 2)° are the vertical angles
42° + 6 (2y – 3)° = 180°
6 (2y°) –  6(3)° = 180° – 42°
12y° – 18° = 138°
12y° = 138° + 18°
12y° = 156°
y° = \(\frac{156}{12}\)
y° = 13°
42° = (8x + 2)°
8x° = 42° – 2°
x° = 40°
x° = \(\frac{40}{8}\)
x° = 5°
So, x° = 5° and y° = 13°

Find the distance from point A to the given line.

Question 4.
A(3, 4), y = – x
Answer:
y = -x
A (3, 4)
y = mx + c
The product of the slopes of the perpendicular lines is equal to -1
m1m2 = -1
(-1) (m2) = -1
m2 = 1
The equation that is perpendicular to the given line equation is x = c
c = 3
The equation that is perpendicular to the given line equation is x = 3
Solving 1 & 2
-x = x – 3
-x – x = -3
2x = 3
x = \(\frac{3}{2}\)
y = -x
y = –\(\frac{3}{2}\)
The point of intersection = (\(\frac{3}{2}\), –\(\frac{3}{2}\))
The points are (3, 4), (\(\frac{3}{2}\), –\(\frac{3}{2}\))
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{30.25 + 2.25}\)
= 5.70

Question 5.
A(- 3, 7), y = \(\frac{1}{3}\)x – 2
Answer:
y = \(\frac{1}{3}\)x – 2
A (-3, 7)
y = mx + c
The product of the slopes of the perpendicular lines is equal to -1
m1m2 = -1
(\(\frac{1}{3}\)) (m2) = -1
m2 = -3
The equation that is perpendicular to the given line equation is y = -3x + c
7 = -3 (-3) + c
c = 7 – 9
c = -2
The equation that is perpendicular to the given line equation is y = -3x – 2
Solving 1 & 2
\(\frac{1}{3}\)x – 2 = -3x – 2
\(\frac{1}{3}\)x + 3x = -2 + 2
x = 0
y = -3x – 2
y = -3 (0) – 2
y = -2
The point of intersection = (0, -2)
The points are: (-3, 7), (0, -2)
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(-2 – 7)² + (0 + 3)²}\)
= 9.48

Find the value of x that makes m || n.

Question 6.

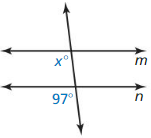
Answer:
From the figure,
x° and 97° are the corresponding angles
According to the Converse of the Corresponding Angles Theorem, m || n is true only when the corresponding angles are congruent
It is given that m || n
x° = 97°

Question 7.

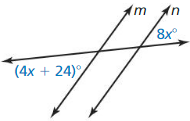
Answer:
From the figure,
8x° and (4x + 24)° are the alternate exterior angles
According to the Converse of the Alternate Exterior Angles Theorem, m || n is true only when the alternate exterior angles are congruent
It is given that m || n
8x° = (4x + 24)°
8x° – 4x° = 24°
4x° = 24°
x° = \(\frac{24}{4}\)
x° = 6°

Question 8.

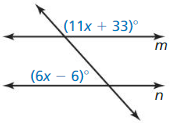
Answer:
From the figure,
(11x + 33)° and (6x – 6)° are the interior angles
According to the Converse of the Interior Angles Theory, m || n is true only when the sum of the interior angles is supplementary
It is given that m || n
(11x + 33)°+(6x – 6)° = 180°
17x° + 27° = 180°
17x° = 180° – 27°
x° = –\(\frac{153}{17}\)
x° = 9°

Write an equation of the line that passes through the given point and is
(a) parallel to and
(b) perpendicular to the given line.

Question 9.
(- 5, 2), y = 2x – 3
Answer:
y= 2x – 3
The given point is: (-5, 2)
a) Parallel to the given line:
The slopes of the parallel lines are the same
y = mx + c
The equation of the line that is parallel to the given line is y = 2x + c
2 = 2 (-5) + c
2 + 10 = c
c = 12
The equation of the line that is parallel to the given line equation is y = 2x + 12
b) Perpendicular to the given line:
The product of the slopes of the perpendicular lines is equal to -1
m1 m2 = -1
2m2 = -1
m2 = –\(\frac{1}{2}\)
The equation of the line that is perpendicular to the given line equation is y = –\(\frac{1}{2}\)x + c
2 = –\(\frac{1}{2}\) (-5) + c
c = –\(\frac{1}{2}\)
The equation of the line that is perpendicular to the given line equation is y = –\(\frac{1}{2}\)x – \(\frac{1}{2}\)

Question 10.
(- 1, – 9), y = – \(\frac{1}{3}\)x + 4
Answer:
y= –\(\frac{1}{3}\)x + 4
(-1, -9)
a) Parallel to the given line:
The slopes of the parallel lines are the same
y = mx + c
The equation of the line that is parallel to the given line is y = –\(\frac{1}{3}\)x + c
-9 = –\(\frac{1}{3}\) (-1) + c
c = \(\frac{26}{3}\)
The equation of the line that is parallel to the given line equation is y = –\(\frac{1}{3}\)x + \(\frac{26}{3}\)
b) Perpendicular to the given line:
The product of the slopes of the perpendicular lines is equal to -1
m1 m2 = -1
–\(\frac{1}{3}\)m2 = -1
m2 = 3
The equation of the line that is perpendicular to the given line equation is y = 3x + c
-9 = 3 (-1) + c
c = -6
The equation of the line that is perpendicular to the given line equation is y = 3x – 6

Question 11.
A student says. “Because j ⊥ K, j ⊥ l’ What missing information is the student assuming from the diagram? Which theorem is the student trying to use?

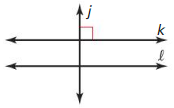
Answer:
Given that a student claimed that j ⊥ K, j ⊥ l
According to the Perpendicular Transversal Theorem,
In a plane, if a line is perpendicular to one of two parallel lines, then it is perpendicular to the other line also.
The line l is also perpendicular to the line j
We can conclude that the theorem student trying to use is the Perpendicular Transversal Theorem

Question 12.
You and your family are visiting some attractions while on vacation. You and your mom visit the shopping mall while your dad and your sister visit the aquarium. You decide to meet at the intersection of lines q and p. Each unit in the coordinate plane corresponds to 50 yards.

Answer:
You and your family are visiting some attractions while on vacation. You and your mom visit the shopping mall while your dad and your sister visit the aquarium. You decide to meet at the intersection of lines q and p. Each unit in the coordinate plane corresponds to 50 yards.

a. Find an equation of line q.
Answer:
From the figure,
The coordinates of line q are (50, 500), (200, 50)
Slope (m) = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{50 – 500}{200 – 50}\)
= \(\frac{-450}{150}\)
= –\(\frac{45}{15}\)
= -3
y – y1 = m (x – x1)
y – 500 = -3 (x -50)
y – 500 = -3x + 150
y = -3x + 150 + 500
y = -3x + 650
The equation of line q is:
y = -3x + 650

b. Find an equation of line p.
Answer:
The coordinates of line p are (50, 175), (500, 325)
Slope (m) = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{325 –  175}{500 – 50}\)
= \(\frac{15}{45}\)
= \(\frac{1}{3}\)
y – y1 = m (x – x1)
y – 175 = \(\frac{1}{3}\) (x -50)
3 (y – 175) = x – 50
3y – 525 = x – 50
3y = x – 50 + 525
3y = x + 475
y = \(\frac{1}{3}\)x + \(\frac{475}{3}\)

c. What are the coordinates of the meeting point?
Answer:
From the figure,
The coordinates of the meeting point are: (150, 200)

d. What is the distance from the meeting point to the subway?
Answer:
From the given figure,
The coordinates of the meeting point are: (150, 200)
The coordinates of the subway are: (500, 300)
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
d = \(\sqrt{(300 – 200)² + (500 – 150)²}\)
d = 364.5 yards

Question 13.
Identify an example on the puzzle cube of each description. Explain your reasoning.

a. a pair of skew lines
Answer:
The “Skew lines” are the lines that are non-intersecting, non-parallel and non-coplanar
From the figure,
We can conclude that the pair of skew lines are \(\overline{A B}\) and \(\overline{G H}\)

b. a pair of perpendicular lines
Answer:
The “Perpendicular lines” are the lines that are intersected at the right angles
The pair of perpendicular lines are \(\overline{I J}\) and \(\overline{C D}\)

c. a pair of paralIeI lines
Answer:
The “parallel lines” are the lines that do not have any intersection point
We can conclude that the pair of parallel lines are \(\overline{C D}\) and \(\overline{E F}\)

d. a pair of congruent corresponding angles
Answer:
∠1 and ∠3 are the corresponding angles

e. a pair of congruent alternate interior angles
Answer:
∠2 and ∠3 are the congruent alternate interior angles

Parallel and Perpendicular Lines Cumulative Assessment

Question 1.
Use the steps in the construction to explain how you know that\(\overline{C D}\) is the perpendicular bisector of \(\overline{A B}\).

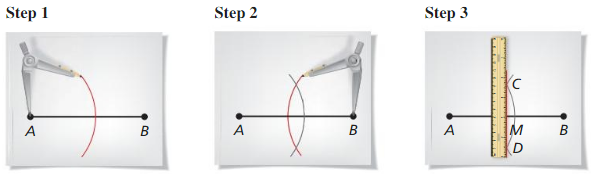
Answer:
1. Draw a line segment of any length and name that line segment AB
2. Draw an arc by using a compass above half of the length of AB by taking the center at A above AB
3. Draw another arc by using a compass above half of the length of AB by taking the center at B above AB
4. Repeat steps 3 and 4 below AB
5. Draw a line segment CD by joining the arcs above and below AB
6. Measure the lengths of the midpoint of AB i.e., AD and DB.
7. By measuring their lengths, we can prove that CD is the perpendicular bisector of AB

Question 2.
The equation of a line is x + 2y = 10.

a. Use the numbers and symbols to create the equation of a line in slope-intercept form
that passes through the point (4, – 5) and is parallel to the given line.
Answer:
The equation of a line is x + 2y = 10.
(4, -5)
The given equation in the slope-intercept form is y = –\(\frac{1}{2}\)x + 5
The equation of the line that is parallel to the given line equation is y = –\(\frac{1}{2}\)x + c
-5 = –\(\frac{1}{2}\) (4) + c
c = -5 + 2
c = -3
Hence, the line that is parallel to the given line equation is y = –\(\frac{1}{2}\)x – 3

b. Use the numbers and symbols to create the equation of a line in slope-intercept form
that passes through the point (2, – 1) and is perpendicular to the given line.
Answer:
x + 2y = 10
(4, -5)
The given equation in the slope-intercept form is y = –\(\frac{1}{2}\)x + 5
The product of the slopes of the perpendicular lines is equal to -1
m1m2 = -1
–\(\frac{1}{2}\) (m2) = -1
m2 = 2
So,
The equation of the line that is perpendicular to the given line equation is y = 2x + c
-5 = 2 (4) + c
-5 – 8 = c
c = -13
We can conclude that a line equation that is perpendicular to the given line equation is y = 2x – 13

Question 3.
Classify each pair of angles whose measurements are given.
a.

Answer:
44° and 136° are the adjacent angles

b.

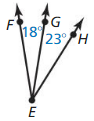
Answer:
18° and 23° are the adjacent angles

c.

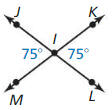
Answer:
75° and 75° are alternate interior angles

d.

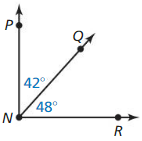
Answer:
42° and 48° are the vertical angles

Question 4.
Your school is installing new turf on the football held. A coordinate plane has been superimposed on a diagram of the football field where 1 unit = 20 feet.

a. What is the length of the field?
Answer:
1 unit = 20 feet
The length of the field = | 20 – 340 |
= 320 feet

b. What is the perimeter of the field?
Answer:
The width of the field = 140 feet
The perimeter of the field = 2 ( Length + Width)
= 2 (320 + 140)
= 2 (460)
= 920 feet

c. Turf costs $2.69 per square foot. Your school has a $1,50,000 budget. Does the school have enough money to purchase new turf for the entire field?
Answer:
The area of the field = Length × Width
The area of the field = 320 × 140
= 44,800 square feet
The total cost of the turf = 44,800 × 2.69
= $1,20,512
It is given that your school has a budget of $1,50,000 but we only need $1,20,512
The school have enough money to purchase new turf for the entire field

Question 5.
Enter a statement or reason in each blank to complete the two-column proof.

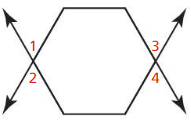
Given ∠1 ≅∠3
Prove ∠2 ≅∠4

Answer:
The given table is:

Hence,
The completed table is:

Question 6.
Your friend claims that lines m and n are parallel. Do you support your friend’s claim? Explain your reasoning.

Answer:
From the figure,
We can observe that 141° and 39° are the consecutive interior angles.
According to the Consecutive Interior Angles Theorem,
If the sum of the angles of the consecutive interior angles is 180°, then the two lines that are cut by a transversal are parallel
The claim of your friend can be supported.

Question 7.
Which of the following is true when are skew?
(A) are parallel.
(B) intersect
(C) are perpendicular
(D) A, B, and C are noncollinear.
Answer:
The “Skew lines” are the lines that are not parallel, non-intersect, and non-coplanar
A, B, and C are noncollinear
Option D is the correct answer.

Question 8.
Select the angle that makes the statement true.

∠1    ∠2    ∠3    ∠4    ∠5     ∠6     ∠7     ∠8
a. ∠4 ≅ ________ b the Alternate Interior Angles Theorem (Thm. 3.2).
Answer:
∠4 ≅ ∠5 Alternate interior angles Theorem,

b. ∠2 ≅ ________ by the Corresponding Angles Theorem (Thm. 3. 1)
Answer:
∠2 ≅ ∠6 Corresponding angles Theorem,

c. ∠1 ≅ ________ by the Alternate Exterior Angles Theorem (Thm. 3.3).
Answer:
∠1 ≅ ∠8 Alternate exterior angles Theorem,

d. m∠6 + m ________ = 180° by the Consecutive Interior Angles Theorem (Thm. 3.4).
Answer:
∠6 + ∠4 = 180° by the Consecutive interior angles Theorem,

Question 9.
You and your friend walk to school together every day. You meet at the halfway point between your houses first and then walk to school. Each unit in the coordinate plane corresponds to 50 yards.

Answer:
It is given that you and your friend walk to school together every day. You meet at the halfway point between your houses first and then walk to school. Each unit in the coordinate plane corresponds to 50 yards.
a. What are the coordinates of the midpoint of the line segment joining the two houses?
Answer:
The midpoint of the line segment joining the two houses is M = (150, 250)

b. What is the distance that the two of you walk together?
Answer:
The coordinates of the school = (400, 300)
The coordinates of the midpoint of the line segment joining the two houses = (150, 250)
It is given the two friends walk together from the midpoint of the houses to the school
d = \(\sqrt{(x2 – x1)² + (y2 – y1)²}\)
= \(\sqrt{(250 – 300)² + (150 – 400)²}\)
= \(\sqrt{2500 + 62,500}\)
= 255 yards