Comparing Angles and Sides in Triangles is a part of the concept of Inequalities in Triangles. I think you are all familiar with SAS and SSS Theorems. Here we will learn deeply about SAS and SSS Inequality theorems with step by step explanation. In addition to that, the students can also find examples for comparing angles and sides in triangles.
Comparison of Sides and Angles in a Triangle
We can determine which angle is largest and which angle is smallest. If one side of the triangle is longer than another side then the angle opposite to the greater side will be greater than the angle opposite to the shorter side. In this section, we will discuss SAS inequality theorem and SSS inequality theorem.
SAS Inequality Theorem:
If two sides of a triangle are congruent to two sides of the other triangle, but the included angle of one triangle has a longer measure than the included angle of another triangle, then the third side of the first triangle is greater than the third side of the second triangle.
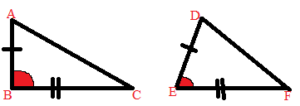
SSS Inequality Theorem:
If two sides of the triangle are congruent to two sides of another triangle, but the third side of the first triangle is greater than the third side of the second triangle, then the included angle of the first triangle’s two congruent sides is greater in measure than the included angle of the second triangle’s two congruent sides.

Comparing Triangle Angles and Sides Examples
Example 1.
In ∆XYZ, ∠XYZ = 40° and ∠YXZ = 71°
Solution:
∠XZY = 180° – (∠XYZ + ∠YXZ)
180° – (40° + 71°)
180° – 111°
= 69°
Therefore
∠XYZ > ∠XZY > ∠YXZ
The greater angle has the greater side opposite to it.
Example 2.
In a ∆PQR, QR = 8cm, PQ = 6cm and PR = 4cm arrange x°, Y° and z° in the ascending order.
Solution:
Given that,
QR > PQ > PR
Therefore ∠QPR > ∠PRQ > ∠PQR as the greater side has the greater angle opposite to it
Therefore
(180° – ∠QPR) < (180° – ∠PRQ) < (180° – ∠PQR)
y° < x° < z°
Example 3.
In ∆XYZ, ∠XYZ = 30° and ∠YXZ = 40°
Solution:
∠XZY = 180° – (∠XYZ + ∠YXZ)
180° – (30° + 40°)
180° – 70°
= 110°
Therefore
∠XYZ > ∠YXZ > ∠XZY
The greater angle has the greater side opposite to it.
Example 4.
In a ∆PQR, QR = 2cm, PQ = 3cm and PR = 4cm arrange x°, Y° and z° in the ascending order.
Solution:
Given that,
QR > PQ > PR
Therefore ∠QPR > ∠PRQ > ∠PQR as the greater side has the greater angle opposite to it
Therefore
(180° – ∠QPR) < (180° – ∠PRQ) < (180° – ∠PQR)
y° < x° < z°
Example 5.
In ∆ABC, ∠ABC = 20° and ∠BAC = 21°
Solution:
∠ACB = 180° – (∠ABC + ∠BAC)
180° – (20° + 21°)
180° – 41°
= 139°
Therefore
∠ACB > ∠BAC > ∠ABC
The greater angle has the greater side opposite to it.
FAQs on Comparison of Sides and Angles in a Triangle
1. What is the relationship between angles and sides of a triangle?
In any triangle, the largest side and largest angle are opposite one another. the smallest side and smallest angle are opposite one another.
2. How do you compare triangle measurements?
If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar.
3. How are sides and angles similar?
In a pair of similar triangles, corresponding sides are proportional and all three angles are congruent.