This article provides you with the converse of the midpoint theorem. Geometry is the branch of mathematics that deals with triangles, spheres, and planes, etc. Basically, a triangle is the smallest polygon formed by three line segments, the midpoint theorem, and converse of the midpoint theorem uses to find the missing values and the midpoints of the sides of the triangle. It deals with some properties of the triangles.
Midpoint theorem is applied in the field of coordinate geometry, algebra, and calculus. On this page, the converse of midpoint theorem statement, proof, and construction of the theorem is provided. Just dive into this page and gain more knowledge on midpoint theorem concepts.
Related Articles:
State and Prove Converse of Mid-Point Theorem
A midpoint is the middle point of a line segment which is equidistant from both the ends. The midpoint theorem works conversely, too because if you draw a line parallel to a side of the triangle over one side’s midpoint, it automatically intersects the midpoint of the other side of the triangle. In the midpoint theorem, four little triangles are created by joining the midpoints that are congruent to one other.
Statement of Converse of Midpoint Theorem
The converse of midpoint theorem states that “If a line is drawn through the midpoint of one side of a triangle, and parallel to the other side, it bisects the third side”.

Prove the Theorem:
Consider the above triangle ABC.
Given D is the midpoint of AB. From D a line DE is drawn parallel to BC, intersect AC at E.
We have to prove that E is the midpoint of AC i.e., AE=CE.
Construction:
From the above triangle ABC, construct a line from C a line parallel to AB is drawn which meets DE produced at F.

The above diagram is the constructed version of △ABC to prove the converse of midpoint theorem.
Proof of Converse of the Midpoint Theorem
Since BD is parallel to CF i.e., BD ∥ CF by the construction.
DF is parallel to BC i.e., DF ∥ BC (given)
Hence, BDFC is a parallelogram.
BD = CF and BC = DF (Opposite sides of the parallelogram are equal)
AD=BD (D is the midpoint of AB)
Therefore, AD=CF (because BD=AD and BD=CF)
In the △ADE and △ECF
∠AED = ∠FEC (Vertically opposite angles)
∠DAE = ∠ECF (Alternate interior angles)
AD=FC (It was proved above)
△ADE ≅ △ECF
Therefore, by AAS congruency, triangles are congruent.
Thus, AE = EC by c.p.c.t
Therefore, E is the midpoint of AC.
Hence, the converse of the midpoint theorem is proved.
Do Check:
Converse of Midpoint Theorem Questions and Answers
Example 1:
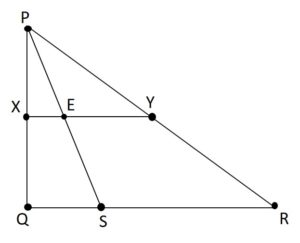
Consider a triangle PQR, and let S be any point on QR. Let X and Y be the midpoints of PQ and PR respectively. Show that XY bisects PS from the given diagram.
Solution:
Given X and Y are the midpoints of PQ and PR.
By the midpoint theorem, XY || QR.
Now, consider the triangle PQS.
Line XE is parallel to the base QS, and X is the midpoint of PQ.
By the converse of the midpoint theorem, E must be the midpoint of PS.
Hence, XY bisects PS.
Example 2:
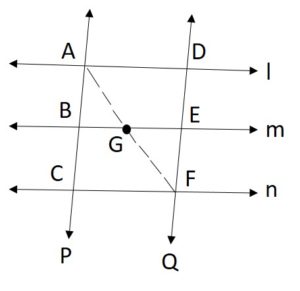
l, m, and n are three parallel lines. P and Q are the transversal intersecting parallel lines at the points A, B, C, D, E, and F as shown in the figure. If AB: BC = 1:1 then find the ratio of DE: EF.
Solution:
Given AB: BC = 1:1
Join AF, which intersects the line m at point G.
In △ACF
AB: BC = 1:1, which implies B is the midpoint of AC.
BG ∥ CF, from given, the lines m and n are parallel.
By the converse of midpoint theorem, “the line drawn from the midpoint parallel to the other side bisects the third side of the triangle”.
Hence, G is the midpoint of AF.
Thus, AG=GF.
Now, in △AFD
AG=GF (Proved above)
GE ∥ AD as the lines l and m are parallel.
Therefore, by the converse of the midpoint theorem,
E is the midpoint of DF.
Thus, DE=EF.
Therefore, the ratio of DE: EF = 1:1.
FAQ’s for the Converse of the Midpoint Theorem
1. What is the converse of the midpoint theorem states?
The converse of the midpoint theorem states that ” In a triangle, the line drawn through the mid-point of one side of a triangle parallel to the base of a triangle bisects the third side of the triangle”.
2. What is the converse of the theorem in geometry?
The converse of a theorem occurs when the conclusion and hypothesis of a theorem are interchanged. For example, if you have a statement that says “if this and then that”, and the converse theorem says that ” if that and then this”. Logically, the result of reversing its two constituent statements.
3. Is the word converse always false?
The fact of the converse theorem statement is not always the same as the original statement says. The converse defines, however, must always be the truth. If this is not the case, then the definition of converse is not valid.