To understand the relation, you need to have a clear idea of the cross-product of two sets. Because a relation is the subset of the cartesian product of two sets. Generally, a set is a collection of well-defined elements and a cartesian product is the product of two sets which has a set of ordered pairs in the form of (a, b). Where a is an element of the first set, b is an element of the second set. Basically, a relation is a rule that related an element from one set to the second element in another set. Get to know more about the domain and range of a relation.
Also, Read:
Domain and Range of a Relation – Definition
Relation: If there are two non-empty sets A, B, then the relation r is defined as the subset of cross-product A x B. That subset is the result of the relation between the elements of both sets. R = {(a, b) : a ∈ A, b ∈ B}.
Domain: The set of elements of the first set belonging to the relation R is called the domain of the relation.
Domain(r) = {a : (a, b) ∈ R}
The domain of relation from A to B is a subset of A.
Range: The set of elements of the second set belonging to the relation R is called the range of the relation.
Range(r) = {b : (a, b) ∈ R}
The range of relation from A to B is a subset of B.
Example:
If two non empty sets are P = {1, 3, 7, 6, 5}, Q = {2, 4, 8, 9, 12}
Then R is the relation “less than” from set P to set Q
The relation R = {(1, 2), (1, 4), (3, 4), (7, 9), (5, 12), (6, 8)}
Therefore, Domain(R) = {1, 3, 5, 6, 7}, Range(R) = {2, 4, 8, 9, 12}
The arrow diagram to represent the domain and range of a relation is
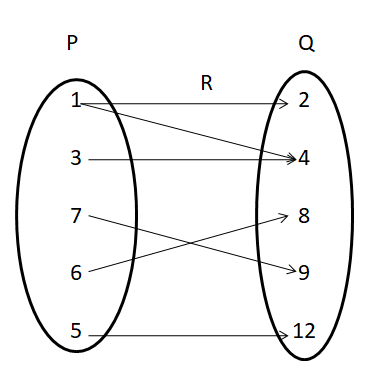
Domain and Range Examples and Answers
Question 1:
If A = {3, 5, 7, 6} and B = {21, 30, 18, 35, 10} and R be the relation ‘is factor of’ from A to B.
(i) Write R in the roster form and find the domain and range of a relation R.
(ii) Draw an arrow diagram to represent the relation.
Solution:
Given that,
A = {3, 5, 7, 6} and B = {21, 30, 18, 35, 10}
(i) R has elements of a, b and a is a factor of B. Where a is an element of A and b is an element of B.
Therefore, relation R in roster form = {(3, 21), (3, 18), (3, 30), (5, 30), (5, 35), (5, 10), (7, 21), (7, 35), (6, 18), (6, 30)}
The domain of the relation R is the set of all first components of R.
Range of relation R is the set of all second components of R.
So, Domain(R) = {3, 5, 6, 7}
Range(R) = {10, 18, 21, 30, 35}
(ii) The arrow diagram to represent R is
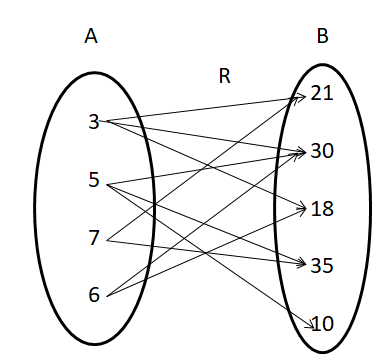
Question 2:
Find the domain and range of the relation R defined by R = {(x + 1, 2x + 3) : x ∈ {1, 2, 3, 4, 5}}
Solution:
Since x = {1, 2, 3, 4, 5}
Therefore,
x = 1 ⇒ x + 1 = 1 + 1 = 2 and 2x + 3 = 2(1) + 3 = 2 + 3 = 5
x = 2 ⇒ x + 1 = 2 + 1 = 3 and 2x + 3 = 2(2) + 3 = 4 + 3 = 7
x = 3 ⇒ x + 1 = 3 + 1 = 4 and 2x + 3 = 2(3) + 3 = 6 + 3 = 9
x = 4 ⇒ x + 1 = 4 + 1 = 5 and 2x + 3 = 2(4) + 3 = 8 + 3 = 11
x = 5 ⇒ x + 1 = 5 + 1 = 6 and 2x + 3 = 2(5) + 3 = 10 + 3 = 13
Hence relation R = {(2, 5), (3, 7), (4, 9), (5, 11), (6, 13)}
Domain of R = {a : (a, b) ∈R} = Set of first components of all ordered pair belonging to R.
Domain(R) = {2, 3, 4, 5, 6}
Range of R = {b : (a, b) ∈ R} = Set of second components of all ordered pairs belonging to R.
Range(R) = {5, 7, 9, 11, 13}
Question 3:
The arrow diagram shows the relation (R) from set A to set B. Write this relation in the roster form. Also, find the domain and range of the relation.
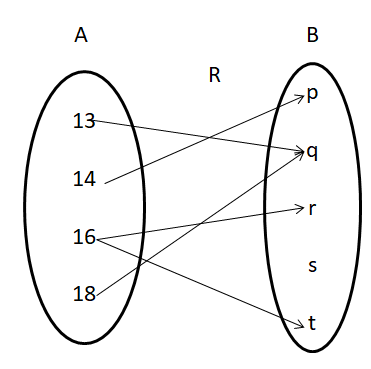
Solution:
R is the relation from A to B.
From the arrow diagram, we can write the relation R = {(13, q), (14, p), (16, r), (14, t), (18, q)}
The relation set R in the roster form = {(13, q), (14, p), (16, r), (14, t), (18, q)}
Domain of R = set of all first components of the relation = {13, 14, 16, 18}
Range of R = set of all second components of the relation = {p, q, r, t}
Question 4:
If X = {4, 5, 6, 8, 9, 10} define the relation R from X to X by R = {(x, y) : y = x + 1}
(i) Draw this relation using an arrow diagram.
(ii) Write domain and range of R.
Solution:
Given set X = {4, 5, 6, 8, 9, 10}
Relation R = {(x, y) : y = x + 1}
If x = 4, then y = x + 1 = 4 + 1 = 5
If x = 5, then y = x + 1 = 5 + 1 = 6
If x = 6, then y = x + 1 = 6 + 1 = 7
If x = 8, then y = x + 1 = 8 + 1 = 9
If x = 9, then y = x + 1 = 9 + 1 = 10
If x = 10, then y = x + 1 = 10 + 1 = 11
Relation R = {4, 5), (5, 6), (8, 9), (9, 10)}
(i) The arrow diagram of relation is
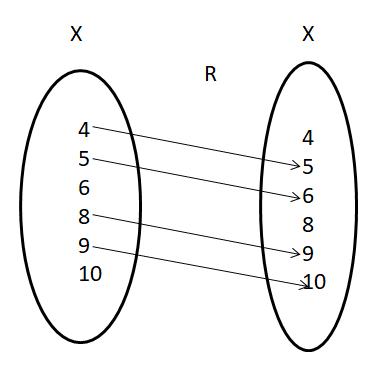
(ii) Domain of the relation = set of first components of all ordered pair belonging to R.
Therefore, domain of R = {4, 5, 8, 9}
Range of the relation = set of second components of all ordered pair belonging to R.
Therefore, range of R = {5, 6, 9, 10}.
FAQs on Domain and Range of a Relation
1. How do you state that domain and range of a relation?
The domain of a relation is nothing but the set of all first components of R and the range of a relation is the set of all second components of R.
2. What is a rule for relation?
Relation a subset of the cartesian product of two sets. And it is a set of ordered pairs which has a relationship between the first set element with the second set element.
3. Write an example for the domain and range?
If relation R = {(1, 4), (2, 5), (3, 6), (4, 7)}, then the domain of relation R is {1, 2, 3, 4} and range of relation R is {4, 5, 6, 7}.
