Eureka Math Algebra 1 Module 1 Lesson 16 Answer Key

Engage NY Eureka Math Algebra 1 Module 1 Lesson 16 Answer Key

Eureka Math Algebra 1 Module 1 Lesson 16 Exercise Answer Key

Exercise 1.
Solve w²=121, for w. Graph the solution on a number line.
Answer:
w=±11

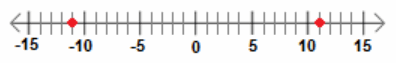
b. Solve w²<121, for w. Graph the solution on a number line, and write the solution set as a compound inequality.
Answer:
-11<w<11

c. Solve w²≥121, for w. Graph the solution on a number line, and write the solution set as a compound inequality.
Answer:
w≤-11 or w≥11

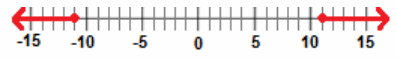
d. Quickly solve (x+7)²=121, for x. Graph the solution on a number line.
Answer:
x=-18 or x=4

e. Use your work from part (d) to quickly graph the solution on a number line to each inequality below.
i. (x+7)²<121
Answer:

ii. (x+7)²≥121
Answer:

Extension
Use the following to challenge students who finish early.
a. Poindexter says that (a+b)² equals a²+2ab+b². Is he correct?
b. Solve x²+14x+49<121, for x. Present the solution graphically on a number line.

Exercises 2–3
Give students four minutes to work on Exercises 2 and 3. Then, discuss the results as a class. Students are applying their knowledge from the previous lesson to solve an unfamiliar type of problem.

Exercise 2.
Consider the compound inequality -5<x<4. a. Rewrite the inequality as a compound statement of inequality. Answer: x>-5 and x<4

b. Write a sentence describing the possible values of x.
Answer:
x can be any number between -5 and 4.

c. Graph the solution set on the number line below.
Answer:

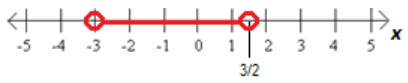
Exercise 3.
Consider the compound inequality -5<2x+1<4. a. Rewrite the inequality as a compound statement of inequality. Answer: 2x+1>-5 and 2x+1<4 b. Solve each inequality for x. Then, write the solution to the compound inequality. Answer: x>-3 and x<\(\frac{3}{2}\) OR -3<x<\(\frac{3}{2}\)

c. Write a sentence describing the possible values of x.
Answer:
x can be any number between -3 and \(\frac{3}{2}\).

d. Graph the solution set on the number line below.
Answer:

Review Exercise 3 with students to demonstrate how to solve it without rewriting it.
→ A friend of mine suggested I could solve the inequality as follows. Is she right?
-5<2x+1<4
-5-1<2x+1-1<4-1
-6<2x<3
-3<x<\(\frac{3}{2}\) Encourage students to articulate their thoughts and scrutinize each other’s reasoning. Point out to students that solving the two inequalities did not require any new skills. They are solved just as they learned in previous lessons. Have students verify their solutions by filling in a few test values. Remind students that the solution can be written two ways: x>-3 and x<\(\frac{3}{2}\) OR -3<x<\(\frac{3}{2}\)

Exercises 4–5
Give students four minutes to work on Exercises 4 and 5. Then, review the results as a class. Again, point out to students that solving the two inequalities did not require any new skills. They are solved just as they learned in previous lessons. Have students verify their solutions by filling in a few test values.

Exercise 4.
Given x<-3 or x>-1:
a. What must be true in order for the compound inequality to be a true statement?
Answer:
One of the statements must be true, so either x has to be less than -3, or it has to be greater than -1. (In this case, it is not possible that both are true.)

b. Write a sentence describing the possible values of x.
Answer:
x can be any number that is less than -3 or any number that is greater than -1.

c. Graph the solution set on the number line below.
Answer:

Exercise 5.
Given x+4<6 or x-1>3:
a. Solve each inequality for x. Then, write the solution to the compound inequality.
Answer:
x<2 or x>4

b. Write a sentence describing the possible values of x.
Answer:
x can be any number that is less than 2 or any number that is greater than 4.

c. Graph the solution set on the number line below.
Answer:

Exercise 6.
Solve each compound inequality for x, and graph the solution on a number line.
a. x+6<8 and x-1>-1

Answer:
x<2 and x>0 → 0<x<2

b. -1≤3-2x≤10

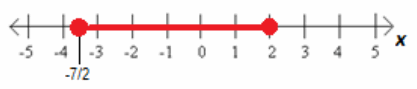
Answer:
x≥-\(\frac{7}{2}\) and x≤2 → –\(\frac{7}{2}\)≤x≤2

c. 5x+1<0 or 8≤x-5

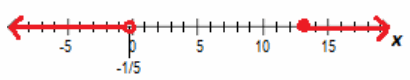
Answer:
x<-\(\frac{1}{5}\) or x≥13 d. 10>3x-2 or x=4

Answer:
x<4 or x=4 → x≤4

e. x-2<4 or x-2>4

Answer:
x<6 or x>6 → x≠6

f. x-2≤4 and x-2≥4

Answer:
x=6

Debrief the exercise with the following questions:
→ Look at the solution to part (f) closely. Remind students that both statements must be true. Therefore, the solution is only x=6.
→ How would the solution to part (f) change if the “and” was an “or”? Let this discussion lead in to Exercise 7.

Exercise 7.
Solve each compound inequality for x, and graph the solution on a number line. Pay careful attention to the inequality symbols and the “and” or “or” statements as you work.
a. 1+x>-4 or 3x-6>-12
Answer:
x>-5

b. 1+x>-4 or 3x-6<-12
Answer:
x can be any real number. c. 1+x>4 and 3x-6<-12 Answer: x>3 and x<-2
No solution (empty set) since there are no numbers that satisfy both statements

Eureka Math Algebra 1 Module 1 Lesson 16 Problem Set Answer Key

Solve each inequality for x, and graph the solution on a number line.

Question 1.
x-2<6 or \(\frac{x}{3}\)>4
Answer:
x<8 or x>12

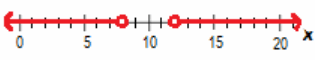
Question 2.
-6<\($\frac{x+1}{4}$\)<3
Answer:
-25<x<11

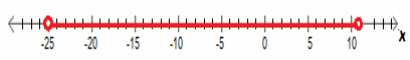
Question 3.
5x≤21+2x or 3(x+1)≥24
Answer:
x≤7 or x≥7 → all real numbers

Question 4.
5x+2≥27 and 3x-1<29
Answer:
x≥5 and x<10 → 5≤x<10

Question 5.
0≤4x-3≤11
Answer:
\(\frac{3}{4}\)≤x≤\(\frac{7}{2}\)

Question 6.
2x>8 or -2x<4
Answer:
x>4 or x>-2 → x>-2

Question 7.
8≥-2(x-9)≥-8
Answer:
5≤x≤13

Question 8.
4x+8>2x-10 or \(\frac{1}{3}\) x-3<2
Answer:
x>-9 or x<15 → all real numbers

Question 9.
7-3x<16 and x+12<-8
Answer:
x>-3 and x<-20 → no solution

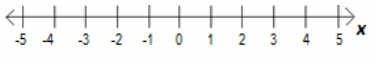
Question 10.
If the inequalities in Problem 8 were joined by “and” instead of “or,” what would the solution set become?
Answer:
-9 < x < 15

Question 11.
If the inequalities in Problem 9 were joined by “or” instead of “and,” what would the solution set become?
Answer:
x > -3 or x < -20

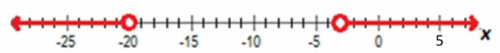
Eureka Math Algebra 1 Module 1 Lesson 16 Exit Ticket Answer Key

Question 1.
Solve each compound inequality for x, and graph the solution on a number line.
a. 9+2x<17 or 7-4x<-9
Answer:
x<4 or x>4 or x≠4

b. 6≤\(\frac{x}{2}\)≤11
Answer:
12 ≤ x ≤ 22

Question 2.
a. Give an example of a compound inequality separated by “or” that has a solution of all real numbers.
Answer:
Sample response: x>0 or x<2 b. Take the example from part (a), and change the “or” to an “and.” Explain why the solution set is no longer all real numbers. Use a graph on a number line as part of your explanation. Answer: Sample response: x>0 and x<2
In the first example, only one of the inequalities needs to be true to make the compound statement true. Any number selected is either greater than 0 or less than 2 or both. In the second example, both inequalities must be true to make the compound statement true. This restricts the solution set to only numbers between 0 and 2.