Engage NY Eureka Math Algebra 1 Module 3 Lesson 21 Answer Key
Eureka Math Algebra 1 Module 3 Lesson 21 Exercise Answer Key
Opening Exercise
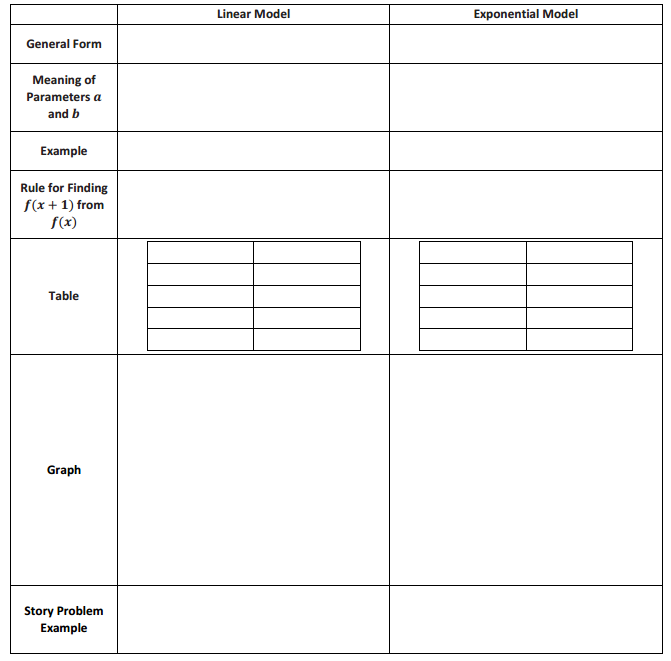
Answer:
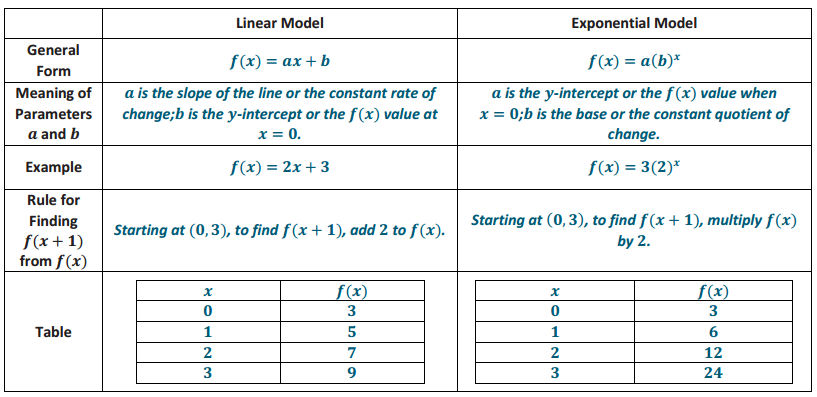
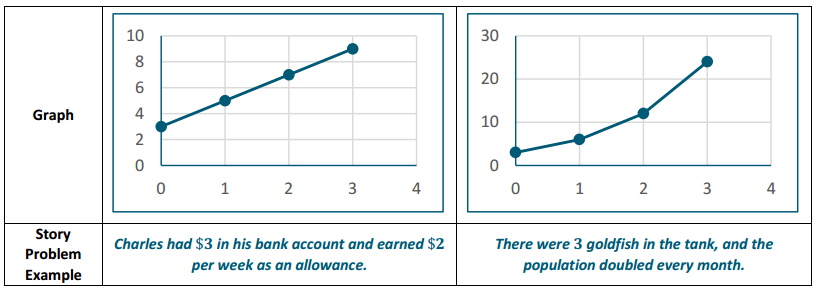
Exercises
Exercise 1.
For each table below, assume the function f is defined for all real numbers. Calculate ∆f = f(x + 1) – f(x) in the last column in the tables below, and show your work. (The symbol ∆ in this context means change in.) What do you notice about ∆f? Could the function be linear or exponential? Write a linear or an exponential function formula that generates the same input – output pairs as given in the table.
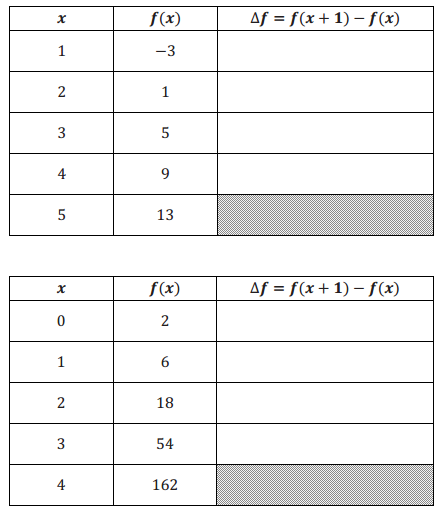
Answer:
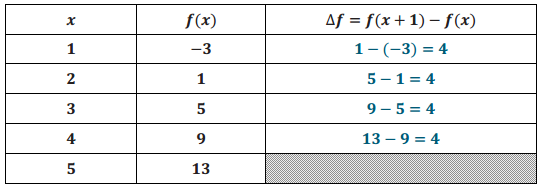
f(x) = 4x – 7
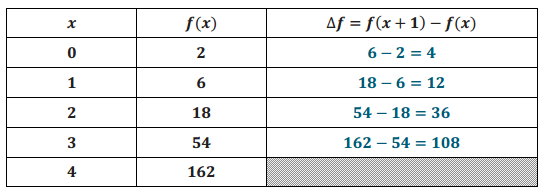
If the entries in the table were considered as a geometric sequence, then the common quotient would be r = 3. Since f(0) = 2, a = 2. Since f(1) = 6, we must have 6 = 2 ⋅ b or b = 3. Hence, f(x) = 2(3)x.
Exercise 2.
Terence looked down the second column of the table below and noticed that \(\frac{3}{1}\) = \(\frac{9}{3}\) = \(\frac{27}{9}\) = \(\frac{81}{27}\). Because of his observation, he claimed that the input – output pairs in this table could be modeled with an exponential function. Explain why Terence is correct or incorrect. If he is correct, write a formula for the exponential function that generates the input – output pairs given in the table. If he is incorrect, determine and write a formula for a function that generates the input – output pairs given in the table.
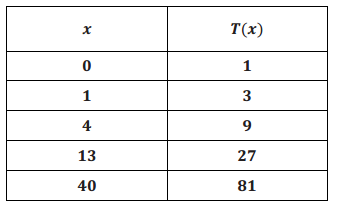
Answer:
Terence is incorrect. This is because the distance between consecutive x – values is not 1 (not constant).
Exercise 3.
A river has an initial minnow population of 40,000 that is growing at 5% per year. Due to environmental conditions, the amount of algae that minnows use for food is decreasing, supporting 1,000 fewer minnows each year. Currently, there is enough algae to support 50,000 minnows. Is the minnow population increasing linearly or exponentially? Is the amount of algae decreasing at a linear or an exponential rate? In what year will the minnow population exceed the amount of algae available?
Answer:
The minnow population is increasing exponentially. The amount of algae is decreasing the food supply that can be used to support minnows linearly. Solution methods to finding when the minnow population will exceed the amount of algae may vary. Here is one solution: We need to find the number of years n such that 40(1.05)n > 50 – n. (Why?) For n = 3, we get 46.3 > 47 is false, but for n = 4, we get that 48.6 > 46 is true. Hence, some time after the third year, the minnow population will exceed the amount of algae available.
Exercise 4.
Using a calculator, Joanna made the following table and then made the following conjecture: 3x is always greater than (1.02)^x. Is Joanna correct? Explain.
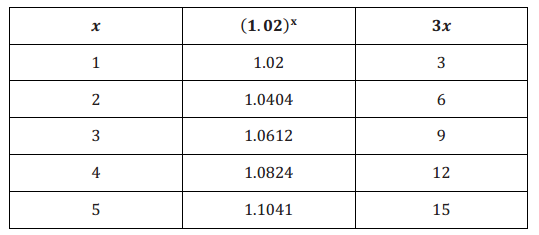
Answer:
The function (1.02)x is exponential, and the function 3x is linear, so the exponential will eventually exceed the linear. (Alternatively, students could extend the table to larger values of x to show that the exponential function will eventually exceed the linear function.) (1.02)500 ≈ 19957, but 3(500) = 1500
Eureka Math Algebra 1 Module 3 Lesson 21 Problem Set Answer Key
For each table in Problems 1–6, classify the data as describing a linear relationship, an exponential growth relationship, an exponential decay relationship, or neither. If the relationship is linear, calculate the constant rate of change (slope), and write a formula for the linear function that models the data. If the function is exponential, calculate the common quotient for input values that are distance one apart, and write the formula for the exponential function that models the data. For each linear or exponential function found, graph the equation y = f(x).
Question 1.
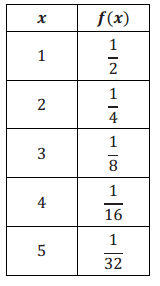
Answer:
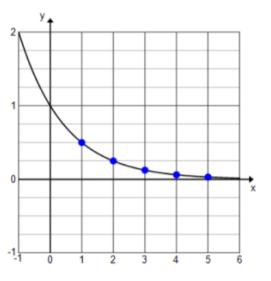
Common quotient: \(\frac{1}{2}\), exponential decay, f(x) = (\(\frac{1}{2}\))x
Question 2.
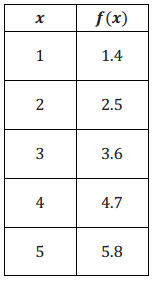
Answer:
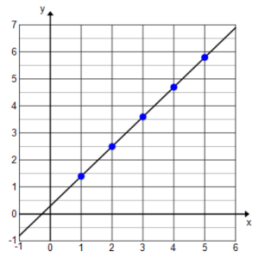
Constant rate of change: 1.1, linear, f(x) = 0.3 + 1.1x
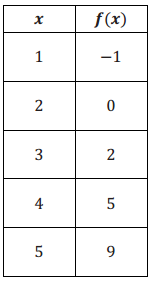
Question 3.
Answer:
Neither
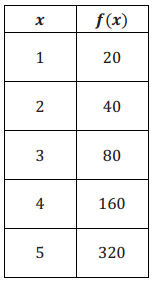
Question 4.
Answer:
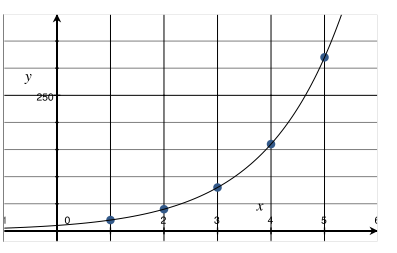
Ratio of change: 2, exponential growth, f(x) = 10(2)x
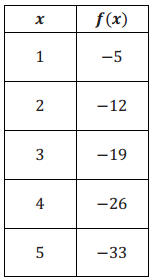
Question 5.
Answer:
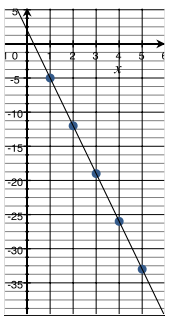
Rate of change: – 7, linear, f(x) = 2 – 7x
Question 6.
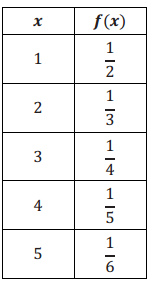
Answer:
Neither
Question 7.
Here is a variation on a classic riddle: Jayden has a dog – walking business. He has two plans. Plan 1 includes walking a dog once a day for a rate of $5 per day. Plan 2 also includes one walk a day but charges 1 cent for 1 day, 2 cents for 2 days, 4 cents for 3 days, and 8 cents for 4 days and continues to double for each additional day. Mrs. Maroney needs Jayden to walk her dog every day for two weeks. Which plan should she choose? Show the work to justify your answer.
Answer:
Plan 1: 5 × 14 = 70 She will pay $70 for two weeks under Plan 1.
Plan 2: The price can be modeled using the function f(x) = 0.01(2)(x – 1), which describes the amount she pays for
x days. Then,
f(14) = 0.01(2)(14 – 1) or f(14) = 81.92.
She will pay $81.92 under Plan 2 for two weeks.
Plan 1 is the better choice.
Question 8.
Tim deposits money in a certificate of deposit account. The balance (in dollars) in his account t years after making the deposit is given by T(t) = 1000(1.06)t for t ≥ 0.
a. Explain, in terms of the structure of the expression used to define T(t), why Tim’s balance can never be $999.
Answer:
(1.06)0 = 1, and positive powers of 1.06 are larger than 1; thus, the minimum value T(t) attains, if t ≥ 0, is 1,000. In the context given, a CD account grows in value over time, so with a deposit of $1,000, the value will never drop to $999.
b. By what percent does the value of T(t) grow each year? Explain by writing a recursive formula for the sequence T(1), T(2), T(3), etc.
Answer:
Writing out the sequence, we see:
Year 1: 1000(1.06)1
Year 2: 1000(1.06)2
Year 3: 1000(1.06)3
.
.
.
Thus, T(n + 1) = T(n)(1.06) or T(n + 1) = T(n) + T(n)(0.06), showing that T(n) grows by 6% per year.
c. By what percentage does the value of T(t) grow every two years? (Hint: Use your recursive formula to write T(n + 2) in terms of T(n).)
Answer:
Since, T(n + 1) = T(n)(1.06), we can write:
T(n + 2) = T(n + 1)(1.06)
= T(n)(1.06)(1.06),
or T(n + 2) = T(n)(1.1236).
Hence, the amount in his account grows by 12.36% every two years.
Question 9.
Your mathematics teacher asks you to sketch a graph of the exponential function f(x) = (\(\frac{3}{2}\))x for x, a number between 0 and 40 inclusively, using a scale of 10 units to one inch for both the x – and y – axes.
a. What are the dimensions (in feet) of the roll of paper needed to sketch this graph?
Answer:
The roll would need to be a bit wider than 4 in. (\(\frac{1}{3}\) ft.) and, after rounding up, about 1,105,734 in. (or 92,145 ft. long).
b. How many more feet of paper would you need to add to the roll in order to graph the function on the interval 0 ≤ x ≤ 41?
Answer:
It would require approximately 46,072 more feet of paper. Teachers: Look for the easy solution, which is f(41) = f(40) × 1.5 = f(40) + f(40) × \(\frac{1}{2}\).
c. Find an m so that the linear function g(x) = mx + 2 is greater than f(x) for all x such that 0 ≤ x ≤ 40, but f(41) > g(41).
Answer:
There are many possible answers: Any number between (roughly) 276,433.275 and 404,536 will do. Note that f(40) ≈ 11 057 332.32 and f(41) ≈ 16 585 998.48, so any slope such that 11 057 333 ≤ g(40) and g(41) ≤ 16 585 998 will do. Since g(40) = 40m + 2, solving 11 057 333 = 40m + 2 or m = 276 433.275 might produce such a linear function. We need to check only that the function g(x) = 276 433.275x + 2 satisfies f(41) > g(41), which it does because g(41) = 11 333 766.275.
Eureka Math Algebra 1 Module 3 Lesson 21 Exit Ticket Answer Key
Question 1.
Here is a classic riddle: Mr. Smith has an apple orchard. He hires his daughter, Lucy, to pick apples and offers her two payment options:
Option A: $1.50 per bushel of apples picked
Option B: 1 cent for picking one bushel, 3 cents for picking two bushels, 9 cents for picking three bushels, and so on, with the amount of money tripling for each additional bushel picked
a. Write a function to model each option.
Answer:
Option A: f(x) = 1.50x, where x is the number of bushels of apples picked
Option B: g(x) = 0.01(3)(x – 1), where x is the number of bushels of apples picked
b. If Lucy picks six bushels of apples, which option should she choose?
Answer:
Option A: $9
Option B: $2.43
Option A is better.
c. If Lucy picks 12 bushels of apples, which option should she choose?
Answer:
Option A: $18
Option B: $1,771.47
Option B is much better.
d. How many bushels of apples does Lucy need to pick to make Option B better for her than Option A?
Answer:
The eighth bushel picked is when the exponential function exceeds the linear function.