Engage NY Eureka Math Algebra 1 Module 3 Lesson 5 Answer Key
Eureka Math Algebra 1 Module 3 Lesson 5 Example Answer Key
Example 1.
Folklore suggests that when the creator of the game of chess showed his invention to the country’s ruler, the ruler was highly impressed. He was so impressed, he told the inventor to name a prize of his choice. The inventor, being rather clever, said he would take a grain of rice on the first square of the chessboard, two grains of rice on the second square of the chessboard, four on the third square, eight on the fourth square, and so on, doubling the number of grains of rice for each successive square. The ruler was surprised, even a little offended, at such a modest prize, but he ordered his treasurer to count out the rice.
a. Why is the ruler surprised? What makes him think the inventor requested a modest prize?
Answer:
The ruler is surprised because he hears a few grains mentioned—it seems very little, but he does not think through the effect of doubling each collection of grains; he does not know that the amount of needed rice will grow exponentially.
The treasurer took more than a week to count the rice in the ruler’s store, only to notify the ruler that it would take more rice than was available in the entire kingdom. Shortly thereafter, as the story goes, the inventor became the new king.
b. Imagine the treasurer counting the needed rice for each of the 64 squares. We know that the first square is assigned a single grain of rice, and each successive square is double the number of grains of rice of the previous square. The following table lists the first five assignments of grains of rice to squares on the board. How can we represent the grains of rice as exponential expressions?

Answer:
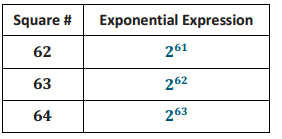
c. Write the exponential expression that describes how much rice is assigned to each of the last three squares of the board.
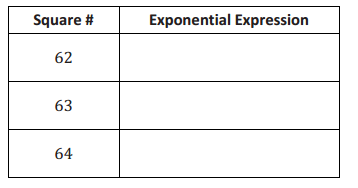
Answer:
Example 2.
Let us understand the difference between f(n) = 2n and f(n) = 2n.
a. Complete the tables below, and then graph the points (n,f(n)) on a coordinate plane for each of the formulas.
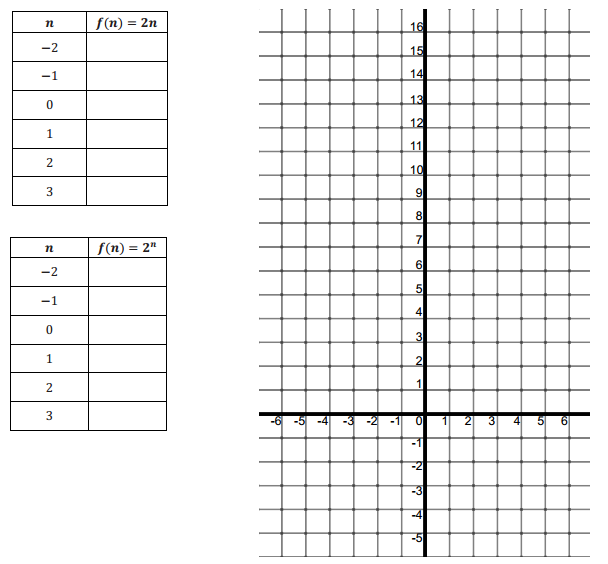
Answer:
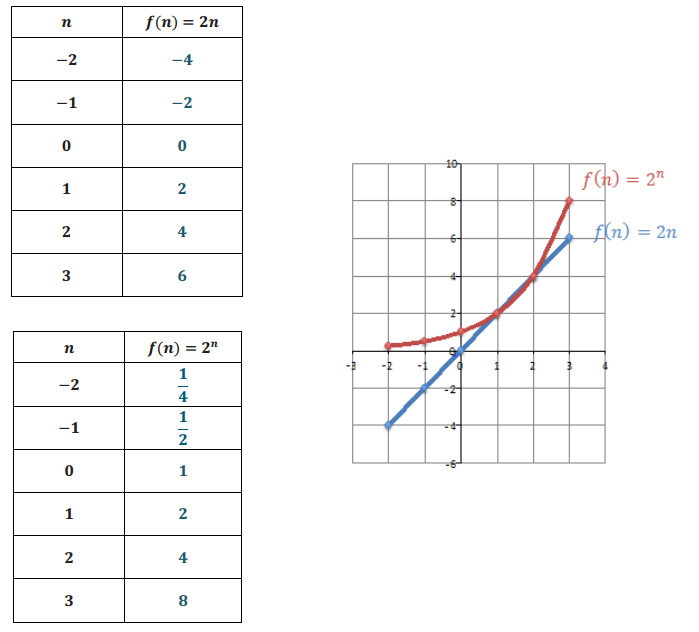
b. Describe the change in each sequence when n increases by 1 unit for each sequence.
Answer:
For the sequence f(n) = 2n, for every increase in n by 1 unit, the f(n) value increases by 2 units. For the sequence f(n) = 2n, for every increase in n by 1 unit, the f(n) value increases by a factor of 2.
Eureka Math Algebra 1 Module 3 Lesson 5 Exercise Answer Key
Opening Exercise
Two equipment rental companies have different penalty policies for returning a piece of equipment late.
Company 1: On day 1, the penalty is $5. On day 2, the penalty is $10. On day 3, the penalty is $15. On day 4, the penalty is $20, and so on, increasing by $5 each day the equipment is late.
Company 2: On day 1, the penalty is $0.01. On day 2, the penalty is $0.02. On day 3, the penalty is $0.04. On day 4, the penalty is $0.08, and so on, doubling in amount each additional day late.
Jim rented a digger from Company 2 because he thought it had the better late return policy. The job he was doing with the digger took longer than he expected, but it did not concern him because the late penalty seemed so reasonable. When he returned the digger 15 days late, he was shocked by the penalty fee. What did he pay, and what would he have paid if he had used Company 1 instead?
Answer:
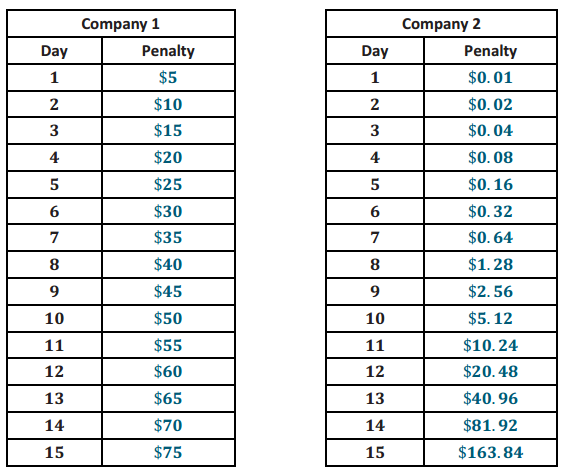
a. Which company has a greater 15-day late charge?
Answer:
Company 2
b. Describe how the amount of the late charge changes from any given day to the next successive day in both Companies 1 and 2.
Answer:
For Company 1, the change from any given day to the next successive day is an increase by $5. For Company 2, the change from any given day to the next successive day is an increase by a factor of 2.
c. How much would the late charge have been after 20 days under Company 2?
Answer:
$5,242.88
Exercise 1.
A typical thickness of toilet paper is 0.001 inch. This seems pretty thin, right? Let’s see what happens when we start folding toilet paper.
a. How thick is the stack of toilet paper after 1 fold? After 2 folds? After 5 folds?
Answer:
After 1 fold: 0.001(21) = 0.002 in.
After 2 folds: 0.001(22) = 0.004 in.
After 5 folds: 0.001(25) = 0.032 in.
b. Write an explicit formula for the sequence that models the thickness of the folded toilet paper after n folds.
Answer:
f(n) = 0.001(2n)
c. After how many folds does the stack of folded toilet paper pass the 1-foot mark?
Answer:
After 14 folds
d. The moon is about 240,000 miles from Earth. Compare the thickness of the toilet paper folded 50 times to the distance from Earth.
Answer:
Toilet paper folded 50 times is approximately 17,769,885 miles thick. That is approximately 74 times the distance between the Earth and the moon.
Exercise 2.
A rare coin appreciates at a rate of 5.2% a year. If the initial value of the coin is $500, after how many years will its value cross the $3,000 mark? Show the formula that models the value of the coin after t years.
Answer:
The value of the coin crosses the $3,000 mark between 35 and 36 years; f(t) = 500(1.052)t.
Eureka Math Algebra 1 Module 3 Lesson 5 Problem Set Answer Key
Question 1.
A bucket is put under a leaking ceiling. The amount of water in the bucket doubles every minute. After 8 minutes, the bucket is full. After how many minutes is the bucket half-full?
Answer:
7 minutes
Question 2.
A three-bedroom house in Burbville sold for $190,000. If housing prices are expected to increase 1.8% annually in that town, write an explicit formula that models the price of the house in t years. Find the price of the house in 5 years.
Answer:
f(t) = 190 000(1.018)t, so f(5) = 190 000(1.018)5 = 207 726.78
In 5 years, the price of the house will be $207,726.78.
Question 3.
A local college has increased its number of graduates by a factor of 1.045 over the previous year for every year since 1999. In 1999, 924 students graduated. What explicit formula models this situation? Approximately how many students will graduate in 2014?
Answer:
f(t) = 924(1.045)t, so f(15) = 924(1.045)15 = 1788
1,788 students are expected to graduate in 2014.
Question 4.
The population growth rate of New York City has fluctuated tremendously in the last 200 years, the highest rate estimated at 126.8% in 1900. In 2001, the population of the city was 8,008,288, up 2.1% from 2000. If we assume that the annual population growth rate stayed at 2.1% from the year 2000 onward, in what year would we expect the population of New York City to have exceeded ten million people? Be sure to include the explicit formula you use to arrive at your answer.
Answer:
f(t) = 8 008 288(1.021)t
Based on this formula, we can expect the population of New York City to exceed ten million people in 2012.
Question 5.
In 2013, a research company found that smartphone shipments (units sold) were up 32.7% worldwide from 2012, with an expectation for the trend to continue. If 959 million units were sold in 2013, how many smartphones can be expected to sell in 2018 at the same growth rate? (Include the explicit formula for the sequence that models this growth.) Can this trend continue?
Answer:
f(t) = 959(1.327)t; f(5) = 959(1.327)5 = 3946
Approximately 3.95 billion units are expected to sell in 2018. No, there are a finite number of people on Earth, so this trend cannot continue.
Question 6.
Two band mates have only 7 days to spread the word about their next performance. Jack thinks they can each pass out 100 fliers a day for 7 days, and they will have done a good job in getting the news out. Meg has a different strategy. She tells 10 of her friends about the performance on the first day and asks each of her 10 friends to each tell a friend on the second day and then everyone who has heard about the concert to tell a friend on the third day, and so on, for 7 days. Make an assumption that students are not telling someone who has not already been told.
a. Over the first 7 days, Meg’s strategy will reach fewer people than Jack’s. Show that this is true.
Answer:
Jack’s strategy: J(t) = 100×7 = 700; therefore, 700 people will know about the concert.
Meg’s strategy: M(t) = 10(2)(t – 1); M(7) = 640; therefore, 640 people will know about the concert.
b. If they had been given more than 7 days, would there be a day on which Meg’s strategy would begin to inform more people than Jack’s strategy? If not, explain why not. If so, on which day would this occur?
Answer:
On the eighth day, Meg’s strategy would reach more people than Jack’s: J(8) = 800; M(8) = 1280.
c. Knowing that she has only 7 days, how can Meg alter her strategy to reach more people than Jack does?
Answer:
She can ask her ten initial friends to tell two people each and let them tell two other people on the next day, etc.
Question 7.
On June 1, a fast-growing species of algae is accidentally introduced into a lake in a city park. It starts to grow and cover the surface of the lake in such a way that the area it covers doubles every day. If it continues to grow unabated, the lake will be totally covered, and the fish in the lake will suffocate. At the rate it is growing, this will happen on June 30.
a. When will the lake be covered halfway?
Answer:
June 29
b. On June 26, a pedestrian who walks by the lake every day warns that the lake will be completely covered soon. Her friend just laughs. Why might her friend be skeptical of the warning?
Answer:
On June 26, the lake will only be 6.25% covered. To the casual observer, it is hard to imagine such a jump between this small percent of coverage to 100% coverage in merely 4 more days.
c. On June 29, a cleanup crew arrives at the lake and removes almost all of the algae. When they are done, only 1% of the surface is covered with algae. How well does this solve the problem of the algae in the lake?
Answer:
It only takes care of the problem for a week:
June 29–1%
June 30–2%
July 1–4%
July 2–8%
July 3–16%
July 4–32%
July 5–64%
By July 6, the lake will be completely covered with algae.
d. Write an explicit formula for the sequence that models the percentage of the surface area of the lake that is covered in algae, a, given the time in days, t, that has passed since the algae was introduced into the lake.
Answer:
f(t) = a(2t)
Question 8.
Mrs. Davis is making a poster of math formulas for her students. She takes the 8.5 in. ×11 in. paper she printed the formulas on to the photocopy machine and enlarges the image so that the length and the width are both 150% of the original. She enlarges the image a total of 3 times before she is satisfied with the size of the poster. Write an explicit formula for the sequence that models the area of the poster, A, after n enlargements. What is the area of the final image compared to the area of the original, expressed as a percent increase and rounded to the nearest percent?
Answer:
The area of the original piece of paper is 93.5 in2. Increasing the length and width by a factor of 1.5 increases the area by a factor of 2.25. Thus, A(n) = 93.5(2.25)n. The area after 3 iterations is approximated by 93.5(11.39) for a result of 1,065 in2. The percent increase is 1,039%.
Eureka Math Algebra 1 Module 3 Lesson 5 Exit Ticket Answer Key
Question 1.
Chain emails are emails with a message suggesting you will have good luck if you forward the email on to others. Suppose a student started a chain email by sending the message to 3 friends and asking those friends to each send the same email to 3 more friends exactly 1 day after receiving it.
a. Write an explicit formula for the sequence that models the number of people who receive the email on the nth day. (Let the first day be the day the original email was sent.) Assume everyone who receives the email follows the directions.
Answer:
f(n) = 3n, n ≥ 1
b. Which day is the first day that the number of people receiving the email exceeds 100?
Answer:
The fifth day