Engage NY Eureka Math Algebra 1 Module 4 Lesson 11 Answer Key
Eureka Math Algebra 1 Module 4 Lesson 11 Example Answer Key
Example
Now try working backward. Rewrite the following standard form quadratic expressions as perfect squares.

Answer:
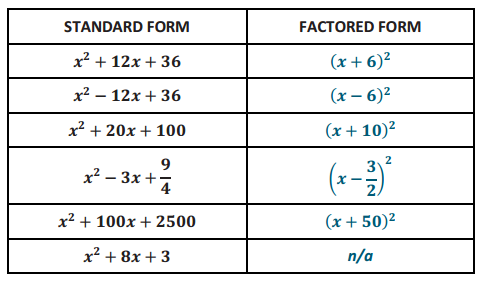
Eureka Math Algebra 1 Module 4 Lesson 11 Exploratory Challenge Answer Key
Exploratory Challenge
Find an expression equivalent to x2 + 8x + 3 that includes a perfect square binomial.
Answer:
(x + 4)2 – 13
Eureka Math Algebra 1 Module 4 Lesson 11 Exercise Answer Key
Opening Exercise
Rewrite the following perfect square quadratic expressions in standard form. Describe patterns in the coefficients for the factored form, (x + A)2, and the standard form, x2 + bx + c.
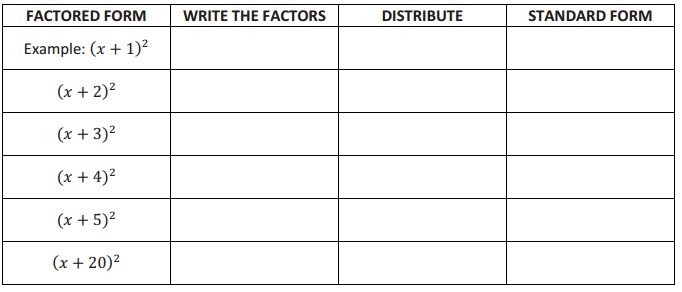
Answer:

For each row, the factored form and standard form are equivalent expressions, so (x + A)2=x2 + bx + c. A, the constant in factored form of the equation, is always half of b, the coefficient of the linear term in the standard form. c, the constant term in the standard form of the quadratic equation, is always the square of the constant in the factored form, A.
Exercises
Rewrite each expression by completing the square.
Exercise 1.
a2 – 4a + 15
Answer:
(a – 2)2 + 11
(Note: Since the constant term required to complete the square is less than the constant term, + 15, students may notice that they just need to split the + 15 strategically.)
Exercise 2.
n2 – 2n – 15
Answer:
(n – 1)2 – 16
Exercise 3.
c2 + 20c – 40
Answer:
(c + 10)2 – 140
Exercise 4.
x2 – 1000x + 60 000
Answer:
(x – 500)2 – 190 000
Exercise 5.
y2 – 3y + 10
Answer:
(y – \(\frac{3}{2}\))2 + \(\frac{31}{4}\)
Exercise 6.
k2 + 7k + 6
Answer:
(k + \(\frac{7}{2}\))2 – \(\frac{25}{4}\)
Exercise 7.
z2 – 0.2z + 1.5
Answer:
(z – 0.1)2 + 1.49
Exercise 8.
p2 + 0.5p + 0.1
Answer:
(p + 0.25)2 + 0.0375
Exercise 9.
j2 – \(\frac{3}{4}\) j + \(\frac{3}{4}\)
Answer:
(j – \(\frac{3}{8}\))2 + \(\frac{39}{64}\)
Exercise 10.
x2 – bx + c
Answer:
(x – \(\frac{b}{2}\))2 + c – \(\frac{b^{2}}{4}\)
Eureka Math Algebra 1 Module 4 Lesson 11 Problem Set Answer Key
Rewrite each expression by completing the square.
Question 1.
q2 + 12q + 32
Answer:
(q + 6)2 – 4
Question 2.
m2 – 4m – 5
Answer:
(m – 2)2 – 9
Question 3.
x2 – 7x + 6.5
Answer:
(x – \(\frac{7}{2}\))2 – 5.75
Question 4.
a2 + 70a + 1225
Answer:
(a + 35)2
Question 5.
z2 – 0.3z + 0.1
Answer:
(z – 0.15)2 + 0.0775
Question 6.
y2 – 6by + 20
Answer:
(y – 3b)2 + 20 – 9b2
Question 7.
Which of these expressions would be most easily rewritten by factoring? Justify your answer.
Answer:
Students may respond with either Problem 1, 2, or 4, and justifications may range from a demonstration of the factoring process to a written explanation where students show that the product – sum rule can be applied to either of these expressions.
Eureka Math Algebra 1 Module 4 Lesson 11 Exit Ticket Answer Key
Question 1.
Rewrite the expression r2 + 4r + 3, first by factoring and then by completing the square. Which way is easier?
Explain why you think so.
Answer:
By factoring: (r + 3)(r + 1)
By completing the square: (r + 2)2 – 1
Both options are fairly simple, and students may select either for their preference. The important thing is that they are thinking about efficiency in their methods and the various options available for rewriting quadratic expressions.