Eureka Math Algebra 2 Module 2 Lesson 16 Answer Key

Engage NY Eureka Math Algebra 2 Module 2 Lesson 16 Answer Key

Eureka Math Algebra 2 Module 2 Lesson 16 Example Answer Key

Example 1: Two Proofs of Our New Identity
Work through these two different ways to approach proving the identity \(\frac{\sin ^{2}(\theta)}{1-\cos (\theta)}\) = 1 + cos θ where θ ≠ 2πk, for integers k. The proofs make use of some of the following properties of equality and real numbers. Here a, b, and c stand for arbitrary real numbers.

Fill in the missing parts of the proofs outlined in the tables below. Then, write a proof of the resulting identity.

a. We start with the Pythagorean identity. When we divide both sides by the same expression, 1 – cos(θ), we introduce potential division by zero when cos(θ) = 1. This will change the set of values of θ for which the identity is valid.
PROOF:

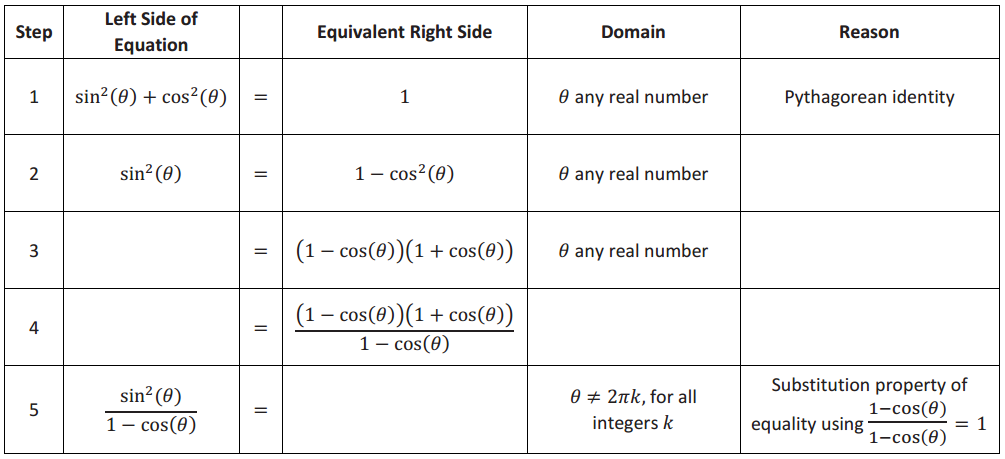
Answer:

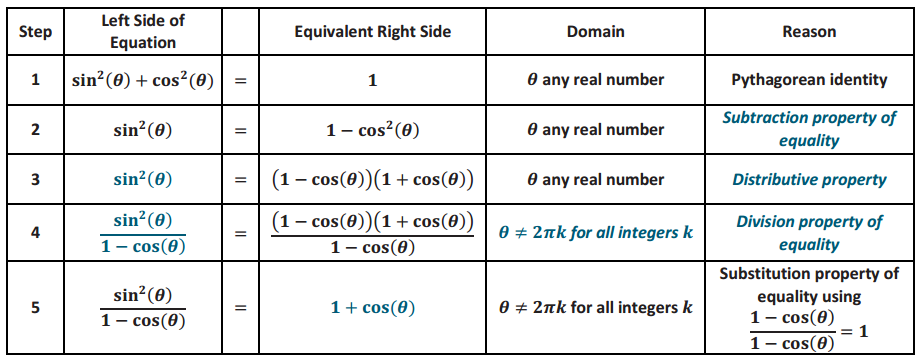
b. Or, we can start with the more complicated side of the identity we want to prove and use algebra and prior trigonometric definitions and identities to transform it to the other side. In this case, the more complicated expression is \(\frac{\sin ^{2}(\theta)}{1-\cos (\theta)}\).
Proof:

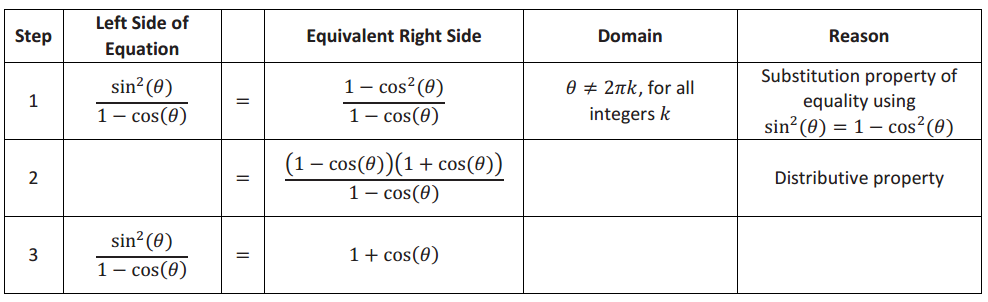
Answer:

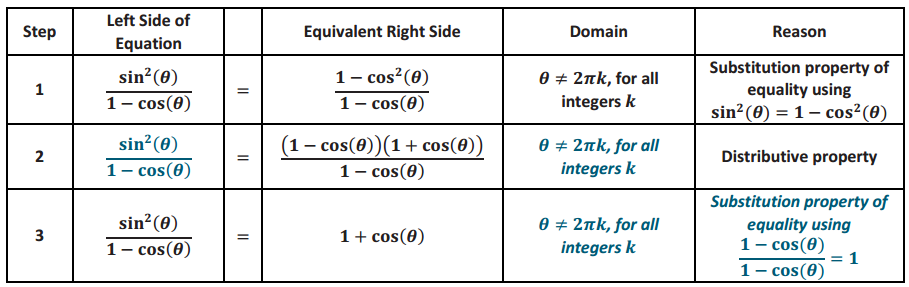
Eureka Math Algebra 2 Module 2 Lesson 16 Opening Exercise Answer Key

Which of these statements is a trigonometric identity? Provide evidence to support your claim.
Statement 1: sin²(θ) = 1 – cos²(θ) for θ any real number.
Statement 2: 1 – cos(θ) = 1 – cos(θ) for θ any real number.
Statement 3: 1 – cos(θ) = 1 + cos(θ) for θ any real number.
Answer:
Statement 1 is found by subtracting cos² (θ) from each side of the Pythagorean identity. Since the Pythagorean identity is true for all real numbers, Statement 1 is also an identity. The functions on either side of the equal sign in Statement 2 are identical, so they are also equivalent. The graphs of the functions on either side of the equal sign in Statement 3 intersect, as shown in the figure below, but the functions are not equivalent. Thus, Statements 1 and 2 are valid identities, but Statement 3 is false.

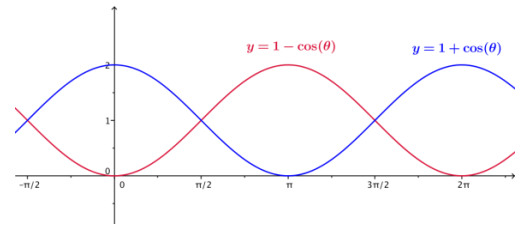
Using Statements 1 and 2, create a third identity, Statement 4, whose left side is \(\frac{\sin ^{2}(\theta)}{1-\cos (\theta)}\).
Answer:
Students are likely to divide the equation in Statement 1 by the equation in Statement 2 to get something like the following statement:

Statement 4: \(\frac{\sin ^{2}(\theta)}{1-\cos (\theta)}\) = 1 + cos(θ) for all θ for which the functions on both sides are defined.

For which values of θ is this statement valid?
Answer:
The left side of the equation in Statement 4 is not defined when cos(θ) = 1, which happens when θ is a multiple of 2π. The right side of the equation is defined for all θ. Thus, the equation is true wherever both sides are defined, which is for all θ that are not multiples of 2π.

Discuss in pairs what it might mean to “prove” an identity. What might it take to prove, for example, that the following statement is an identity?
\(\frac{\sin ^{2}(\theta)}{1-\cos (\theta)}\) = 1 + cos(θ) where θ ≠ 2πk, for all integers k.
Answer:
Students might come up with various suggestions, such as \(\frac{\sin ^{2}(\theta)}{1-\cos (\theta)}\) = 1 + cos(θ), for θ ≠ 2πk for all integers k is an identity if \(\frac{\sin ^{2}(\theta)}{1-\cos (\theta)}\) and 1 + cos(θ) define the same functions or if they take the same values for the variable θ. The functions on the two sides should have the same domain, but that alone is not enough to make the statement an identity.

Eureka Math Algebra 2 Module 2 Lesson 16 Exercise Answer Key

Exercise 1.
Use a calculator to graph the functions f(x) = sin(x) + cos(x) and g(x) = – \(\sqrt{1+2 \sin (x) \cos (x)}\) to determine whether sin(θ) + cos(θ) = –\(\sqrt{1+2 \sin (\theta) \cos (\theta)}\) for all θ for which both functions are defined is a valid identity. You should see from the graphs that the functions are not equivalent.

Suppose that Charles did not think to graph the equations to see if the given statement was a valid identity, so he set about proving the identity using algebra and a previous identity. His argument is shown below.
First, [1] sin(θ) + cos(θ) = –\(\sqrt{1+2 \sin (\theta) \cos (\theta)}\) for θ any real number.
Now, using the multiplication property of equality, square both sides, which gives
[2] sin²(θ) + 2sin(θ)cos(θ) + cos²(θ) = 1 + 2sin(θ)cos(θ) for θ any real number.
Using the subtraction property of equality, subtract 2sin(θ)cos(θ) from each side, which gives
[3] sin²(θ) + cos²(θ) = 1 for θ any real number.
Statement [3] is the Pythagorean identity. So, replace sin² (θ) + cos²(θ) by 1 to get
[4] 1 = 1, which is definitely true.
Therefore, the original statement must be true.

Does this mean that Charles has proven that statement [1] is an identity? Discuss with your group whether it is a valid proof. If you decide it is not a valid proof, then discuss with your group how and where his argument went wrong.
Answer:
No, statement [1] is not an identity; in fact, it is not true, as we showed above by graphing the functions on the two sides of the equation. The sequence of statements is not a proof because it starts with a false statement in statement [1]. Squaring both sides of the equation is an irreversible step thatalters the solutions to the equation. When squaring both sides of an equation, we have assumed that the equality exists, and that amounts to assuming what one is trying to prove. A better approach to prove an identity is valid would be to take one side of the equation in the proposed identity and work on it until one gets the other side.

Exercises 2 – 3

Prove that the following are trigonometric identities, beginning with the side of the equation that seems to be more complicated and starting the proof by restricting x to values where the identity is valid. Make sure that the complete identity statement is included at the end of the proof.

Exercise 2.
tan(x) = \(\frac{\sec (x)}{\csc (x)}\) for real numbers x ≠ \(\frac{\pi}{2}\) + πk, for all integers k.
Answer:
The more complicated side of the equation is \(\frac{\sec (x)}{\csc (x)}\), so we begin with it. First, we eliminate values of x that are not in the domain.
PROOF: Let x be a real number so that x ≠ \(\frac{\pi}{2}\) + πk, for all Integers k.
Applying the definitions of the secant and cosecant functions, we have

Exercise 3.
cot(x) + tan(x) = sec(x)csc(x) for all real numbers x ≠ \(\frac{\pi}{2}\) for integer n.
Answer:
The sides seem equally complicated, but the left side has two terms, so we begin with it. In general, functions composed of multiple terms (or a product of multiple terms) can be seen as more complicated than functions having a single term. However, a valid proof can be written starting on either side of the equation.

PROOF: Let x be a real number so that x ≠ \(\frac{\pi}{2}\)k, for all integers k. Then, we express cot(x) + tan(x) in terms of sin(x) and cos(x) and find a common denominator.

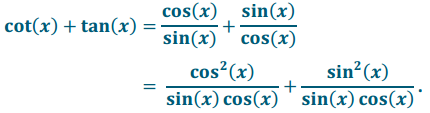
Adding and applying the Pythagorean identity and then converting to the secant and cotangent functions gives

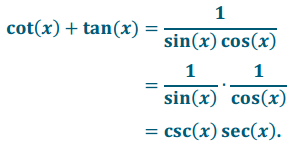
Therefore, cot(x) + tan(x) = sec(x) csc(x), where x ≠ \(\frac{\pi}{2}\)n for all integers n.

Eureka Math Algebra 2 Module 2 Lesson 16 Problem Set Answer Key

Question 1.
Does sin(x + y) equal sin(x) + sin(y) for all real numbers x and y?
a. Find each of the following: sin\(\left(\frac{\pi}{2}\right)\), sin\(\left(\frac{\pi}{4}\right)\), sin\(\left(\frac{3 \pi}{4}\right)\).
Answer:

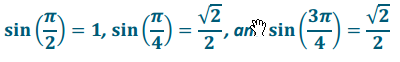
b. Are sin\(\left(\frac{\pi}{2}+\frac{\pi}{4}\right)\) and sin\([latex]\left(\frac{\pi}{2}\right)\)[/latex] + sin\([latex]\left(\frac{\pi}{4}\right)\)[/latex] equal?
Answer:

c. Are there any values of x and y for which sin(x + y) = sin(x) + sin(y)?
Answer:
Yes. If either x or y is zero, or if both x and y are multiples of π, this is a true statement. In many other cases it is not true, so it is not true in general.

Question 2.
Use tan(x) = \(\frac{\sin (x)}{\cos (x)}\) and identities involving the sine and cosine functions to establish the following identities for the tangent function. Identify the values of x where the equation is an identity.
a. tan(π – x) = tan(x)
Answer:
Let x be a real number so that x ≠ \(\frac{\sin (x)}{\cos (x)}\) + πk, for any integer k. Then,

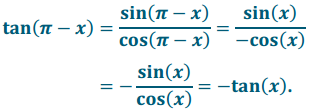
Thus, tan(π – x) = – tan(x), where x ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.

b. tan(x + π) = tan (x)
Answer:
Let x be a real number so that x ≠ \(\frac{\sin (x)}{\cos (x)}\) + πk, for any integer k. Then,

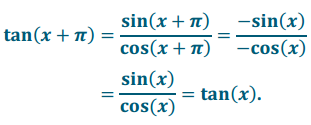
Thus, tan(π – x) = – tan(x), where x ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.

c. tan(2π – x) = – tan(x)
Answer:
Let x be a real number so that x ≠ \(\frac{\sin (x)}{\cos (x)}\) + πk, for any integer k. Then,

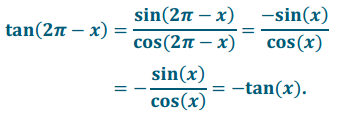
Thus, tan(π – x) = – tan(x), where x ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.

d. tan(- x) = – tan(x)
Answer:
Let x be a real number so that x ≠ \(\frac{\sin (x)}{\cos (x)}\) + πk, for any integer k. Then,

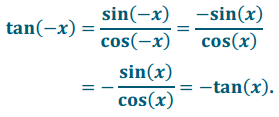
Thus, tan(π – x) = – tan(x), where x ≠ \(\frac{\pi}{2}\) + kπ, for all integers k.

Question 3.
Rewrite each of the following expressions as a single term. Identify the values of x for which the original expression and your expression are equal:
a. cot(x)sec(x)sin(x)
Answer:

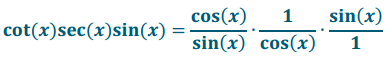
The expressions are equal where x ≠ \(\frac{\pi}{2}\) k, for all integers k.

b. \(\left(\frac{1}{1-\sin (x)}\right)\left(\frac{1}{1+\sin (x)}\right)\)
Answer:

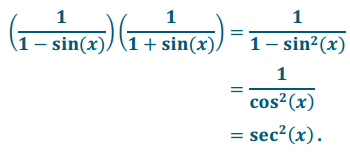
The expressions are equal where x ≠ \(\frac{\pi}{2}\) kπ, for all integers k.

c. \(\frac{1}{\cos ^{2}(x)}-\frac{1}{\cot ^{2}(x)}\)
Answer:

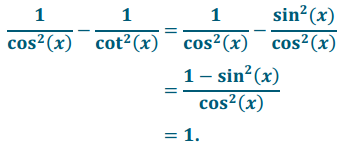
The expressions are equal where x ≠ \(\frac{\pi}{2}\) k, for all integers k.

d. \(\frac{(\tan (x)-\sin (x))(1+\cos (x))}{\sin ^{3}(x)}\)
Answer:

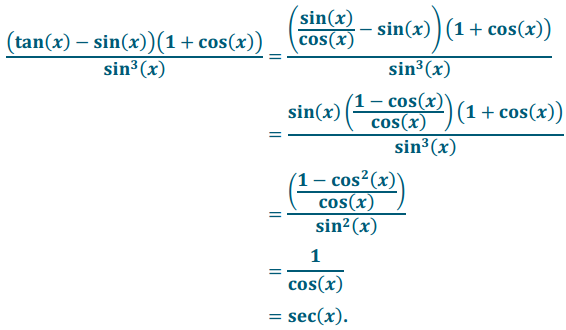
The expressions are equal where x ≠ \(\frac{\pi}{2}\) kπ, for all integers k.

Question 4.
Prove that for any two real numbers a and b,
sin²(a) – sin²(b) + cos²(a) sin²(b) – sin²(a) cos²(b) = 0.
Answer:
PROOF: Let a and b be any real numbers. Then,
sin²(a) – sin²(b) + cos²(a)sin²(b) – sin²(a)cos²(b) = sin²(a)(1 – cos²(b)) – sin²(b)(1 – cos²(a))
= sin²(a)²(b) – sin²(b)sin²(a)
= 0
Therefore, sin²(a) – sin²(b) + cos²(a) sin²(b) – sin²(a) cos²(b) = 0, for all real numbers a and b.

Question 5.
Prove that the following statements are identities for all values of θ for which both sides are defined, and describe that set.
a. cot(θ)sec(θ) = csc(θ)
Answer:
PROOF: Let θ be a real number so that θ ≠ \(\frac{\pi}{2}\) k, for all integers k. Then,

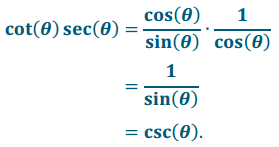
Therefore, cot(θ)sec(θ) = csc(θ), for all values of θ ≠ \(\frac{\pi}{2}\) k for all integers k.

b. (csc(θ) + cot(θ))(1 – cos(θ)) = sin(θ)
Answer:
PROOF: Let θ be a real number so that θ ≠ \(\frac{\pi}{2}\) k, for all integers k. Then,

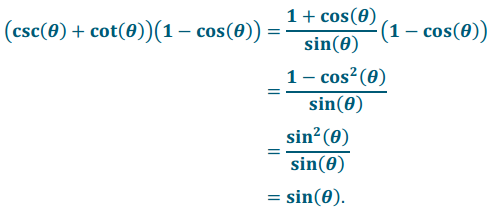
Therefore, (csc(θ) + cot(θ))(1 – cos(θ)) = sin(θ), for all values of θ ≠ \(\frac{\pi}{2}\) k for all integers k.

c. tan²(θ) – sin²(θ) = tan²(θ) sin²(θ)
Answer:
PROOF: Let θ be a real number so that θ ≠ \(\frac{\pi}{2}\) k, for all integers k. Then,

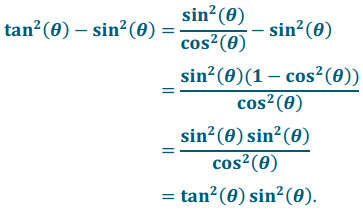
Therefore, tan²(θ) – sin²(θ) = tan²(θ) sin²(θ), for all values of θ ≠ \(\frac{\pi}{2}\) k for all integers k.

d. \(\frac{4+\tan ^{2}(x)-\sec ^{2}(x)}{\csc ^{2}(x)}\) = 3 sin²(x).
Answer:
PROOF: Let x be a real number so that x ≠ \(\frac{\pi}{2}\)k, for all integers k. Then,

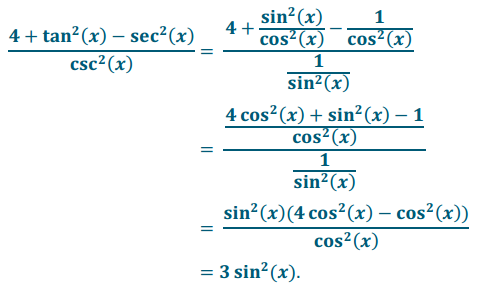
Therefore \(\frac{4+\tan ^{2}(x)-\sec ^{2}(x)}{\csc ^{2}(x)}\) = 3 sin²(x), for all x ≠ \(\frac{\pi}{2}\) k for any integer k.

e. \(\frac{(1+\sin (\theta))^{2}+\cos ^{2}(\theta)}{1+\sin (\theta)}\) = 2
Answer:
PROOF: Let θ be a real number so that θ ≠ – \(\frac{\pi}{2}\) + 2kπ, for all integers k. Then,

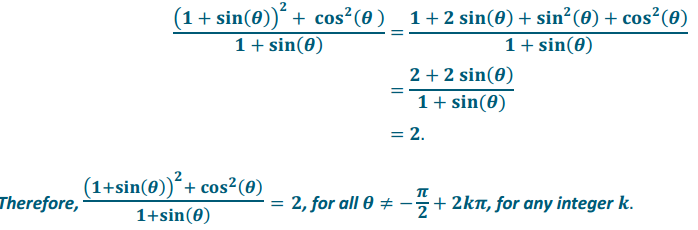
Question 6.
Prove that the value of the following expression does not depend on the value of y:
coy(y)\(\frac{\tan (x)+\tan (y)}{\cot (x)+\cot (y)}\).
Answer:

Eureka Math Algebra 2 Module 2 Lesson 16 Exit Ticket Answer Key

Prove the following identity:
tan(θ) sin(θ) + cos(θ) = sec(θ) for real numbers θ, where θ ≠ \(\frac{\pi}{2}\) + πk, for all integers k.
Answer:
Begin with the more complicated side. Find a common denominator, use the Pythagorean identity, and then convert the fraction to its reciprocal.
PROOF: Let θ be any real number so that θ ≠ \(\frac{\pi}{2}\) + πk, for all integers k. Then,

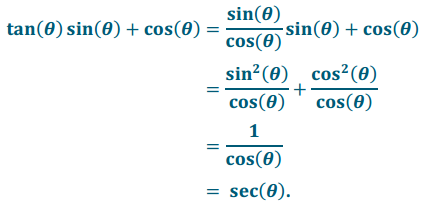
Therefore, tan(θ) sin(θ) + cos(θ) = sec(θ), where θ ≠ \(\frac{\pi}{2}\) + πk, for all integers k.