Engage NY Eureka Math Geometry Module 1 Lesson 21 Answer Key
Eureka Math Geometry Module 1 Lesson 21 Example Answer Key
Example
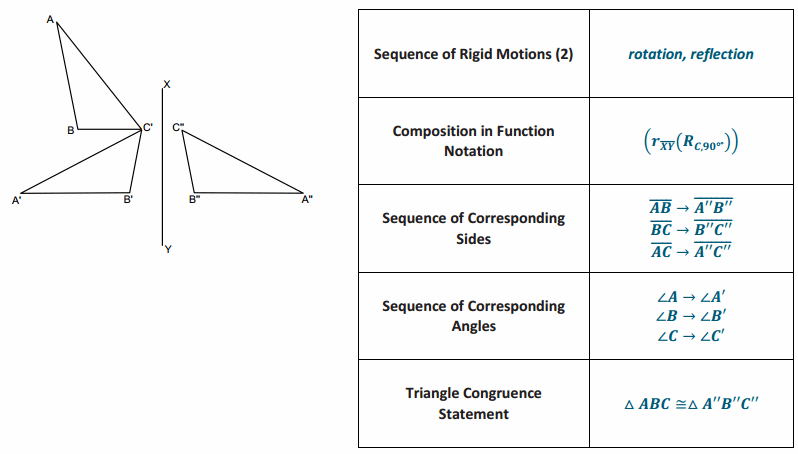
ABCD is a square, and \(\overline{A C}\) is one diagonal of the square. △ABC is a reflection of △ADC across segment AC. Complete the table below, identifying the missing corresponding angles and sides.

Answer:

a. Are the corresponding sides and angles congruent? Justify your response.
Answer:
Since a reflection is a rigid transformation, all angles and sides maintain their size.
b. Is △ABC≅ △ADC? Justify your response.
Answer:
Yes, since △ADC is a reflection of △ABC, they must be congruent.
Eureka Math Geometry Module 1 Lesson 21 Exercise Answer Key
Opening Exercise
The figure to the right represents a rotation of △ABC 80° around vertex C. Name the triangle formed by the image of △ABC. Write the rotation in function notation, and name all corresponding angles and sides.
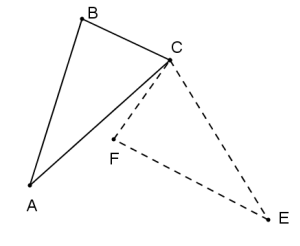
Answer:
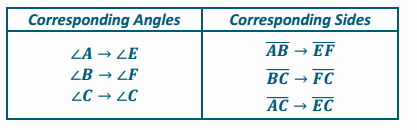
△EFC
RD,80°(△EFC)
Discussion
In the Opening Exercise, we explicitly showed a single rigid motion, which mapped every side and every angle of △ABC onto △EFC. Each corresponding pair of sides and each corresponding pair of angles was congruent. When each side and each angle on the pre-image maps onto its corresponding side or angle on the image, the two triangles are congruent. Conversely, if two triangles are congruent, then each side and angle on the pre-image is congruent to its corresponding side or angle on the image.
Exercises
Each exercise below shows a sequence of rigid motions that map a pre-image onto a final image. Identify each rigid motion in the sequence, writing the composition using function notation. Trace the congruence of each set of corresponding sides and angles through all steps in the sequence, proving that the pre-image is congruent to the final image by showing that every side and every angle in the pre-image maps onto its corresponding side and angle in the image. Finally, make a statement about the congruence of the pre-image and final image.
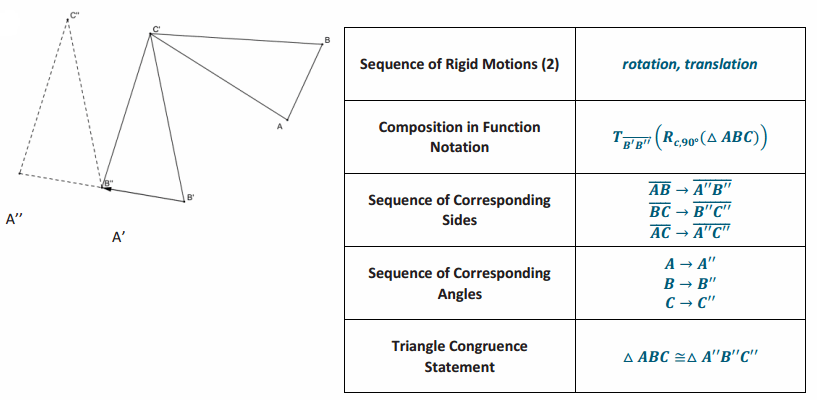
Exercise 1.
Answer:
Exercise 2.
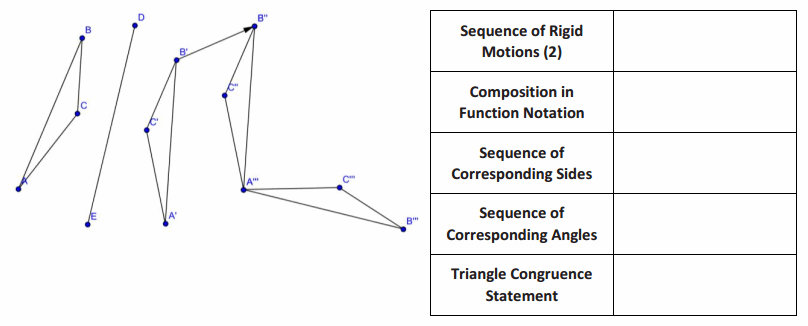
Answer:

Exercise 3.
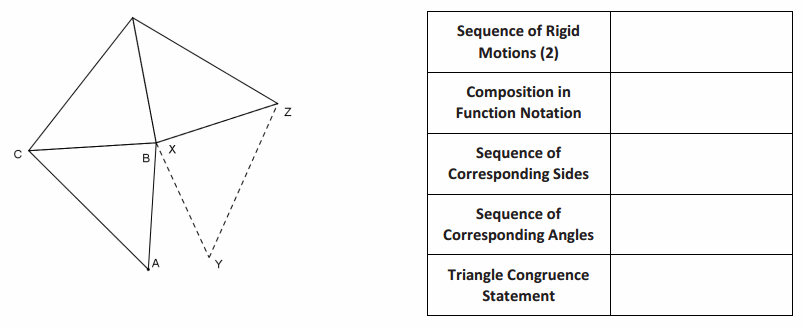
Answer:
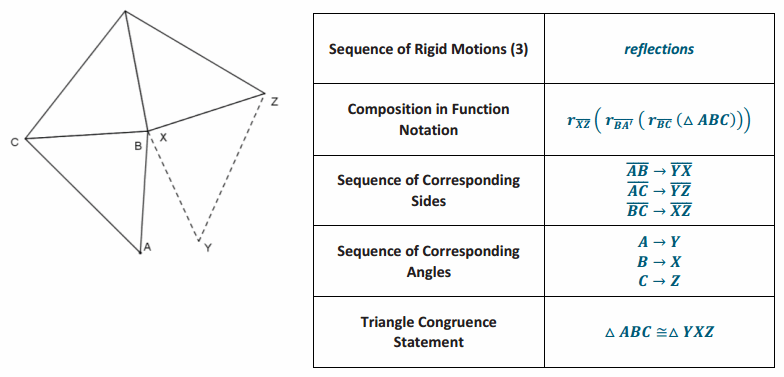
Eureka Math Geometry Module 1 Lesson 21 Problem Set Answer Key
Question 1.
Exercise 3 mapped △ABC onto △YXZ in three steps. Construct a fourth step that would map △YXZ back onto △ABC.
Answer:
Construct an angle bisector for the ∠ABY, and reflect △YXZ over that line.
Question 2.
Explain triangle congruence in terms of rigid motions. Use the terms corresponding sides and corresponding angles in your explanation.
Answer:
Triangle congruence can be found using a series of rigid motions in which you map an original or pre-image of a figure onto itself. By doing so, all the corresponding sides and angles of the figure map onto their matching corresponding sides or angles, which proves the figures are congruent.
Eureka Math Geometry Module 1 Lesson 21 Exit Ticket Answer Key
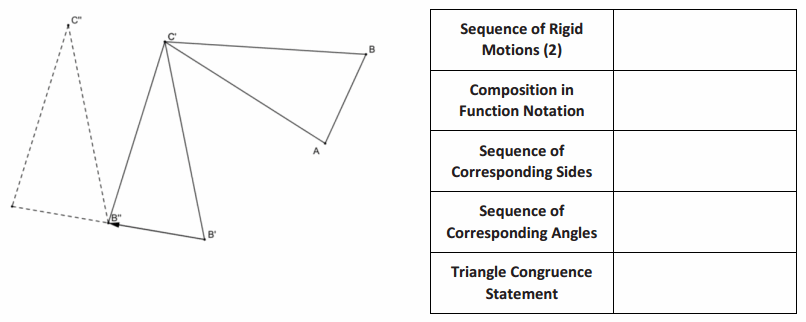
Complete the table based on the series of rigid motions performed on △ABC below.
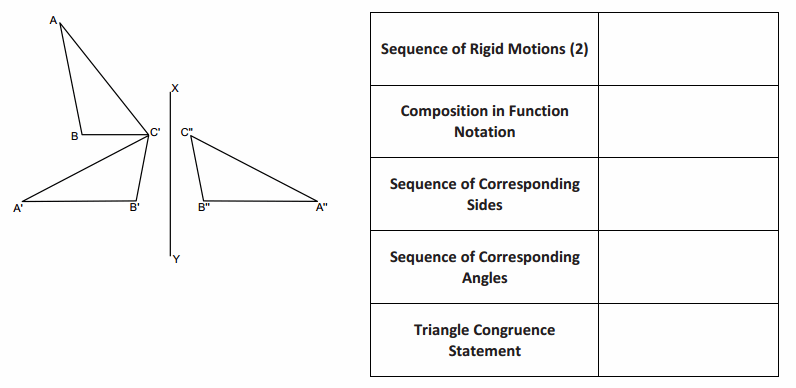
Answer: