Engage NY Eureka Math Geometry Module 1 Lesson 27 Answer Key
Eureka Math Geometry Module 1 Lesson 27 Exercise Answer Key
Exercises
Exercise 1.
Given: AB=AC, RB=RC
Prove: SB=SC
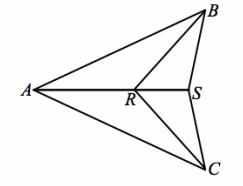
Answer:
AB=AC, RB=RC Given
AR=AR Reflexive property
△ARC≅ △ARB SSS
m∠ARC=m∠ARB Corresponding angles of congruent triangles are equal in measure.
m∠ARC+m∠SRC=180°,
m∠ARB+m∠SRB=180° Linear pairs form supplementary angles.
m∠SRC=m∠SRB Angles supplementary to either the same angle or to congruent angles are equal in measure.
SR=RS Reflexive property
△SRB≅ △SRC SAS
SB=SC Corresponding sides of congruent angles are equal in length.
Exercise 2.
Given: Square ABCS ≅ Square EFGS,
\(\overleftrightarrow{\boldsymbol{R A B}}\), \(\overleftrightarrow{\boldsymbol{R E F}}\)
Prove: △ASR≅ △ESR
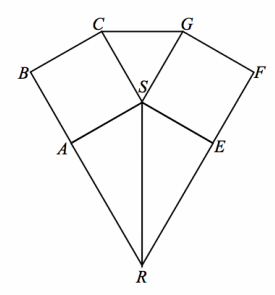
Answer:
Square ABCS ≅ Square EFGS Given
AS=ES Corresponding sides of congruent squares are equal in length.
SR=RS Reflexive property
∠BAS and ∠FES are right angles. Definition of square
∠BAS and ∠SAR form a linear pair. Definition of linear pair
∠FES and ∠SER form a linear pair. Definition of linear pair
∠SAR and ∠SER are right angles. Two angles that are supplementary and congruent each measure 90° and are, therefore, right angles.
△ASR and △ESR are right triangles. Definition of right triangle
△ASR≅ △ESR HL
Exercise 3.
Given: JK=JL, JX=JY
Prove: KX=LY
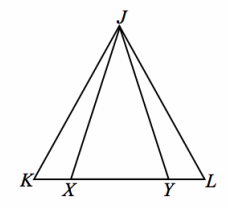
Answer:
JX=JY Given
m∠JXY=m∠JYX Base angles of an isosceles triangle are equal in measure.
m∠JXK+m∠JXY=180°,
m∠JYL+m∠JYX=180° Linear pairs form supplementary angles.
m∠JXK+m∠JXY=m∠JYL+m∠JYX Substitution property of equality
m∠JXK+m∠JXY=m∠JYL+m∠JXY Substitution property of equality
m∠JXK=m∠JYL Angles supplementary to either the same angle or congruent angles are equal in measure.
JK=JL Given
m∠K=m∠L Base angles of an isosceles triangle are equal in measure.
△JXK≅ △JYL AAS
KX=LY Corresponding sides of congruent triangles are equal in length.
Exercise 4.
Given: \(\overline{A D}\) ⊥\(\overline{D R}\), \(\overline{A B}\) ⊥\(\overline{B R}\),
\(\overline{A D}\) ≅ \(\overline{A B}\)
Prove: ∠DCR≅∠BCR
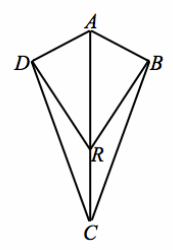
Answer:
\(\overline{A D}\) ⊥\(\overline{D R}\), \(\overline{A B}\) ⊥\(\overline{B R}\) Given
△ADR and △ABR are right triangles. Definition of right triangle
\(\overline{A D}\) ≅ \(\overline{A B}\) Given
\(\overline{A R}\) ≅ \(\overline{A R}\) Reflexive property
△ADR≅ △ABR HL
∠ARD≅ARB Corresponding angles of congruent triangles are congruent.
m∠ARD+m∠DRC=180°,
m∠ARB+m∠BRC=180° Linear pairs form supplementary angles.
m∠ARD+m∠DRC=m∠ARB+m∠BRC Transitive property
m∠DRC=m∠BRC Angles supplementary to either the same angle or congruent angles are equal in measure.
\(\overline{D R}\) ≅ \(\overline{B R}\) Corresponding sides of congruent triangles are congruent.
\(\overline{R C}\) ≅\(\overline{R C}\) Reflexive property
△DRC≅ △BRC SAS
∠DRC≅∠BRC Corresponding angles of congruent triangles are congruent.
Exercise 5.
Given: AR=AS, BR=CS,
\(\overline{R X}\) ⊥\(\overline{A B}\), \(\overline{S Y}\) ⊥\(\overline{A C}\)
Prove: BX=CY
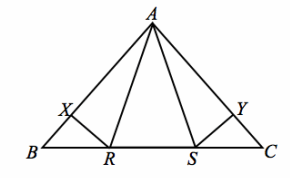
Answer:
AR=AS Given
m∠ARS=m∠ASR Base angles of an isosceles triangle are equal in measure.
m∠ARS+m∠ARB=180°,
m∠ASR+m∠ASC=180° Linear pairs form supplementary angles.
m∠ARS+m∠ARB=m∠ASR+m∠ASC Transitive property
m∠ARB=m∠ASC Subtraction
BR=CS Given
△ARB≅ △ASC SAS
∠ABR≅∠ACS Corresponding angles of congruent triangles are congruent.
\(\overline{R X}\) ⊥\(\overline{A B}\), \(\overline{S Y}\) ⊥\(\overline{A C}\) Given
m∠RXB=90°=m∠SYC Definition of perpendicular line segments
△BRX≅ △SYC AAS
BX=CY Corresponding sides of congruent triangles are equal in length.
Exercise 6.
Given: AX=BX, m∠AMB=m∠AYZ=90°
Prove: NY=NM
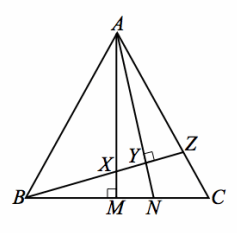
Answer:
AX=BX Given
m∠AMB=m∠AYZ=90° Given
m∠BXM=m∠AXY Vertical angles are equal in measure.
△BXM≅△AXY AAS
BX+XY=BY, AX+XM=AM Segment addition property
XM=XY Corresponding sides of congruent triangles are equal in length.
BY=AM Substitution property of equality
m∠BYN=90° Vertical angles are equal in measure.
m∠AMB+m∠AMN=180° Linear pairs form supplementary angles.
m∠AMN=90° Subtraction property of equality
m∠MNY=m∠MNY Reflexive property
△BYN≅ △AMN AAS
NY=NM Corresponding sides of congruent triangles are equal in length.
Eureka Math Geometry Module 1 Lesson 27 Problem Set Answer Key
Use your knowledge of triangle congruence criteria to write a proof for the following:
In the figure \(\overline{B E}\) ≅ \(\overline{C E}\), \(\overline{D C}\) ⊥\(\overline{A B}\), and \(\overline{B E}\) ⊥\(\overline{A C}\) ; prove \(\overline{A E}\) ≅ \(\overline{R E}\).
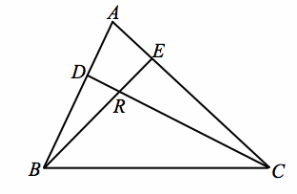
Answer:
m∠ERC=m∠BRD Vertical angles are equal in measure.
\(\overline{D C}\) ⊥\(\overline{A B}\), \(\overline{B E}\) ⊥\(\overline{A C}\) Given
m∠BDR=90°, m∠REC=90° Definition of perpendicular lines
m∠ABE=m∠RCE Sum of the angle measures in a triangle is 180°.
m∠BAE=m∠BRD Sum of the angle measures in a triangle is 180°.
m∠BAE=m∠ERC Substitution property of equality
\(\overline{B E}\) ≅ \(\overline{C E}\) Given
△BAE≅ △CRE AAS
\(\overline{A E}\) ≅\(\overline{R E}\) Corresponding sides of congruent triangles are congruent.
Eureka Math Geometry Module 1 Lesson 27 Exit Ticket Answer Key
Given: M is the midpoint of \(\overline{G R}\), ∠G ≅∠R
Prove: △GHM≅ △RPM
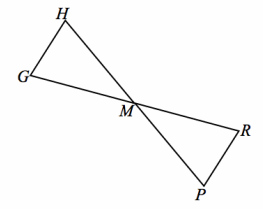
Answer:
M is the midpoint of \(\overline{G R}\). Given
∠G ≅ ∠R Given
GM=RM Definition of midpoint
∠HMG ≅ ∠PMR Vertical angles are congruent.
△GHM≅ △RPM ASA