Engage NY Eureka Math Geometry Module 1 Lesson 9 Answer Key
Eureka Math Geometry Module 1 Lesson 9 Exercise Answer Key
Opening Exercise
One of the main goals in studying geometry is to develop your ability to reason critically, to draw valid conclusions based upon observations and proven facts. Master detectives do this sort of thing all the time. Take a look as Sherlock Holmes uses seemingly insignificant observations to draw amazing conclusions.
Could you follow Sherlock Holmes’s reasoning as he described his thought process?
Discussion
In geometry, we follow a similar deductive thought process (much like Holmes uses) to prove geometric claims.
Let’s revisit an old friend—solving for unknown angles. Remember this one?
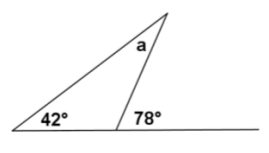
You needed to figure out the measure of a and used the “fact” that an exterior angle of a triangle equals the sum of the measures of the opposite interior angles. The measure of ∠a must, therefore, be 36°.
Suppose that we rearrange the diagram just a little bit.
Instead of using numbers, we use variables to represent angle measures.
Suppose further that we already know that the angles of a triangle sum to 180°. Given the labeled diagram to the right, can we prove that x+y=z (or, in other words, that the exterior angle of a triangle equals the sum of the measures of the opposite interior angles)?
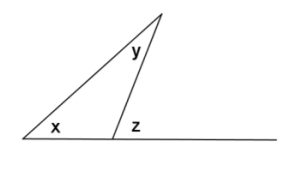
PROOF:
Label ∠w, as shown in the diagram.
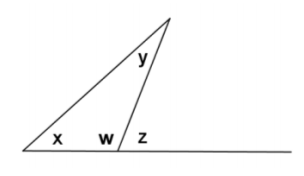
m∠x+m∠y+m∠w=180° The sum of the angle measures in a triangle is 180°.
m∠w+m∠z =180° Linear pairs form supplementary angles.
m∠x+m∠y +m∠w=m∠w+m∠z Substitution property of equality
∴ m∠x +m∠y =m∠z Subtraction property of equality
Notice that each step in the proof was justified by a previously known or demonstrated fact. We end up with a newly proven fact (that an exterior angle of any triangle is the sum of the measures of the opposite interior angles of the triangle). This ability to identify the steps used to reach a conclusion based on known facts is deductive reasoning
(i.e., the same type of reasoning that Sherlock Holmes used to accurately describe the doctor’s attacker in the video clip).
Exercises 1–6
Exercise 1.
You know that angles on a line sum to 180°.
Prove that vertical angles are equal in measure.
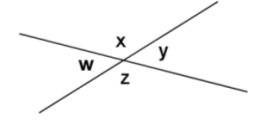
Make a plan:
→ What do you know about ∠w and ∠x? ∠y and ∠x?
Answer:
They sum to 180°.
→ What conclusion can you draw based on both pieces of knowledge?
Answer:
m∠w=m∠y
→ Write out your proof:
Answer:
m∠w+m∠x=180° Linear pairs form supplementary angles.
m∠y+m∠x=180° Linear pairs form supplementary angles.
m∠w+m∠x=m∠y+m∠x Substitution property of equality
∴ m∠w=m∠y Subtraction property of equality
Exercise 2.
Given the diagram to the right, prove that m∠w+ m∠x+ m∠z=180°.
(Make a plan first. What do you know about ∠x, ∠y, and ∠z?)
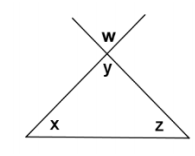
Answer:
m∠y +m∠x+m∠z=180° The sum of the angles of a triangle is 180°.
m∠y=m∠w Vertical angles are equal in measure.
∴ m∠w+m∠x+m∠z=180° Substitution property of equality
Given the diagram to the right, prove that m∠w=m∠y+m∠z.
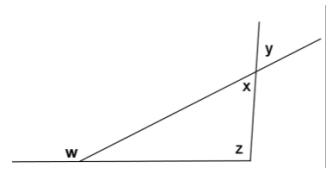
Answer:
m∠w=m∠x+m∠z The exterior angle of a triangle equals the sum of the
two opposite interior angles.
m∠x=m∠y Vertical angles are equal in
measure.
∴ m∠w=m∠y+m∠z Substitution property of equality
Exercise 3.
In the diagram to the right, prove that m∠y+m∠z=m∠w+m∠x.
(You need to write a label in the diagram that is not labeled yet for this proof.)
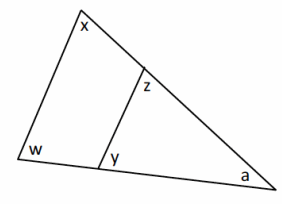
Answer:
m∠a+m∠x+m∠w=180° The sum of the angles of a triangle is 180°.
m∠a+m∠z+m∠y=180° The sum of the angles of a triangle is 180°.
m∠a+m∠x+m∠w=m∠a+m∠z+m∠y Substitution property of equality
∴m∠x+m∠w=m∠z+m∠y Subtraction property of equality
Exercise 4.
In the figure to the right, \(\overline{A B}\) || \(\overline{C D}\) and \(\overline{B C}\) || \(\overline{D E}\). Prove that m∠ABC=m∠CDE.
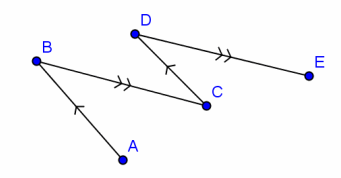
Answer:
\(\overline{A B}\) || \(\overline{C D}\), \(\overline{B C}\) || \(\overline{D E}\) Given
m∠ABC=m∠DCB When two parallel lines are cut by a transversal, the alternate interior angles are equal in measure.
m∠DCB=m∠CDE When two parallel lines are cut by a transversal, the alternate interior angles are equal in measure.
∴ m∠ABC=m∠CDE Substitution property of equality
Exercise 5.
In the figure to the right, prove that the sum of the angles marked by arrows is 900°.
(You need to write several labels in the diagram for this proof.)
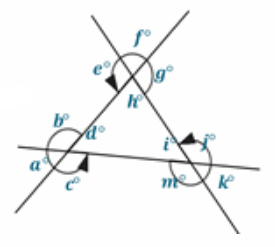
Answer:
a+b+c+d=360 Angles at a point sum to 360°.
e+f+g+h=360 Angles at a point sum to 360°.
i+j+k+m=360 Angles at a point sum to 360°.
a+b+c+d+e+f+g+h+i+j+k+m=1080 Addition property of quality
d+h+i=180 The sum of the angle measures in a triangle is 180°.
a+b+c+e+f+g+j+k+m+180=1080 Substitution property of equality
∴ a+b+c+e+f+g+j+k+m=900 Subtraction property of equality
Exercise 6.
In the figure to the right, prove that \(\overline{D C}\) ⊥ \(\overline{E F}\). Draw in label Z.
Answer:
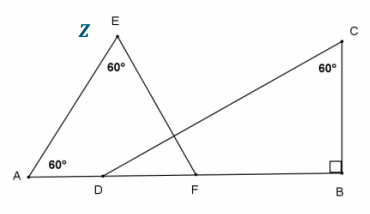
m∠E+m∠A+m∠EFA=180° The sum of the angle measures in a triangle is 180°.
m∠EFA=60° Subtraction property of equality
m∠B+m∠C+m∠CDB=180° The sum of the angle measures in a triangle is 180°.
m∠CDB=30° Subtraction property of equality
m∠CDB+m∠EFA+m∠EZC=180° The sum of the angle measures in a triangle is 180°.
m∠EZC=90° Subtraction property of equality
\(\overline{D C}\) ⊥ \(\overline{E F}\) Perpendicular lines form 90° angles.
Eureka Math Geometry Module 1 Lesson 9 Problem Set Answer Key
Question 1.
In the figure to the right, prove that m || n.
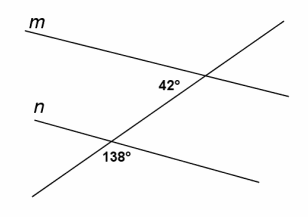
Answer:
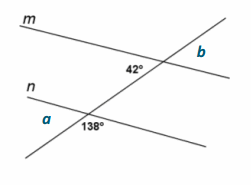
m∠a+138°=180° Linear pairs form supplementary angles.
m∠b=42° Vertical angles are equal in measure.
m∠a=42° Subtraction property of equality
m∠a=m∠b Substitution property of equality
∴ m || n If two lines are cut by a transversal such that a pair of alternate interior angles are equal in meaure, then the lines are parallel.
Question 2.
In the diagram to the right, prove that the sum of the angles marked by arrows is 360°.
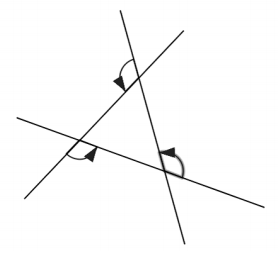
Answer:
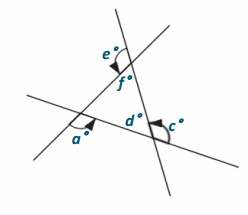
a+b=180 Linear pairs form supplementary angles.
c+d=180 Linear pairs form supplementary angles.
e+f=180 Linear pairs form supplementary angles.
a+b+c+d+e+f=540 Addition property of equality
b+d+f=180 The sum of the angle measures in a triangle is 180°.
∴ a+c+e=360 Subtraction property of equality
Question 3.
In the diagram to the right, prove that m∠a+m∠d-m∠b=180°.
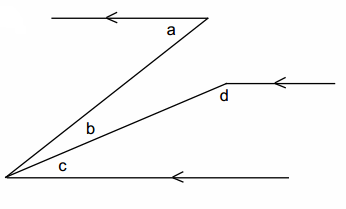
Answer:
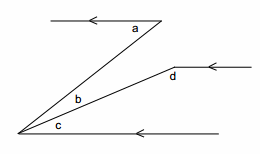
m∠a =m∠b+m∠c If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
m∠c+m∠d=180° If parallel lines are cut by a transversal, then interior angles on the same side are supplementary.
m∠a-m∠b+m∠d=180° Addition of zero/additive identity property
m∠a+m∠d-m∠b=180° Substitution property of equality
Eureka Math Geometry Module 1 Lesson 9 Exit Ticket Answer Key
In the diagram to the right, prove that the sum of the labeled angles is 180°.
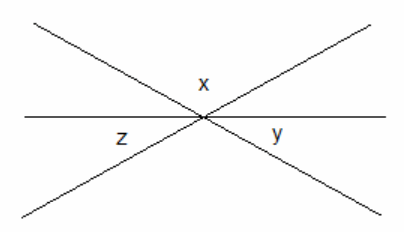
Answer:
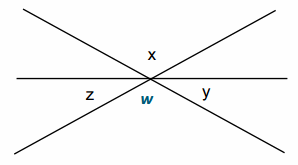
Label ∠w, vertical to ∠x.
m∠w=m∠x Vertical angles are equal in measure.
m∠z +m∠w+m∠y=180° Angles on a line sum to 180°.
m∠z+m∠x +m∠y=180° Substitution property of equality