Engage NY Eureka Math Geometry Module 2 Lesson 4 Answer Key
Eureka Math Geometry Module 2 Lesson 4 Opening Exercise Answer Key
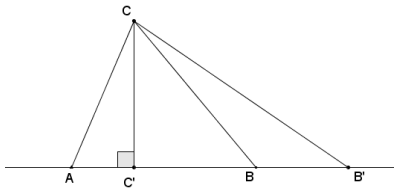
a. Suppose two triangles, ∆ ABC and ∆ ABD, share the same base \(\overline{A B}\) such that points C and D lie on a line parallel to 
. Show that their areas are equal, that is, Area(∆ ABC) = Area(∆ ABD). (Hint: Why are the altitudes of each triangle equal in length?)
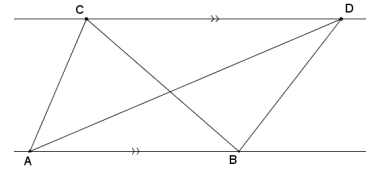
Answer:
Draw a perpendicular line to through C, and label the intersection of both lines C’. Then \(\overline{C C^{\prime}}\) is an altitude
for ∆ ABC. Do the same for ∆ ABD to get an altitude \(\overline{D D^{\prime}}\).
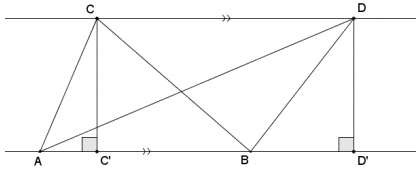
Quadrilateral CC’D ‘D is a parallelogram and, therefore, CC’ = DD’, both of which follow from the properties of parallelograms. Since \(\overline{C C^{\prime}}\) and \(\overline{D D^{\prime}}\) are altitudes of the triangles, we get by the area formula for triangles,
Area(∆ ABC) = \(\frac{1}{2}\)AB ∙ CC’ = \(\frac{1}{2}\)AB ∙ DD’ = Area(∆ ABD).
b. Suppose two triangles have different-length bases, \(\overline{A B}\) and \(\overline{A B^{\prime}}\), that lie on the same line. Furthermore, suppose they both have the same vertex C opposite these bases. Show that the value of the ratio of their areas is equal to the value of the ratio of the lengths of their bases, that is,
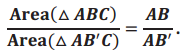
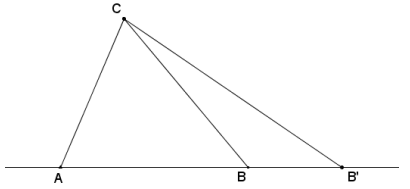
Answer:
Draw a perpendicular line to through C, and label the intersection of both lines C’.
Then \(\overline{C C^{\prime}}\) is an altitude for both triangles.
By the area formula for triangles,
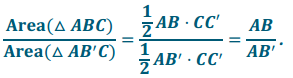
Restatement of the triangle side splitter theorem:
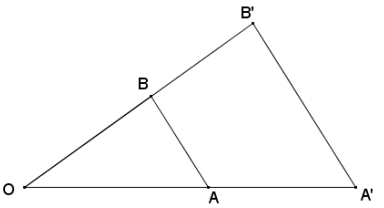
Answer:
In ∆ OA’B’, \(\overline{A B}\) splits the sides proportionally (i.e., = \(\frac{O A^{\prime}}{O A}=\frac{O B^{\prime}}{O B}\) if and only if \(\overline{A^{\prime} B^{\prime}}\) || \(\overline{A B}\).
→ Ask students to relate the restatement of the triangle side splitter theorem to the two theorems above. In order for students to do this, they need to translate the statement into one about dilations. Begin with the implication that \(\overline{A B}\) splits the sides proportionally.
→ What does \(\frac{O A^{\prime}}{O A}=\frac{O B^{\prime}}{O B}\) mean in terms of dilations?
→ This means that there is a dilation with scale factor r = \(\frac{O A^{\prime}}{O A}\) such that Do,r(A) = A’ and Do,r(B) = B’.
→ Which method (parallel or ratio) does the statement “\(\overline{A B}\) splits the sides proportionally” correspond to?
The ratio method
→ What does the ratio ⇒ parallel theorem imply about B’?
This implies that B’ can be found by constructing a line l parallel to \(\overline{A B}\) through A’ and intersecting
that line with \frac{O B^{\prime}}{O A}.
→ Since \(\overline{A B}\) || l, what does that imply about \(\overline{A^{\prime} B^{\prime}}\) and \(\overline{A B}\)?
The two segments are also parallel as in the triangle side splitter theorem.
→ Now, suppose that \(\overline{A^{\prime} B^{\prime}}\) || \(\overline{A B}[/latexas in the picture below. Which method (parallel or ratio) does this statement correspond to?
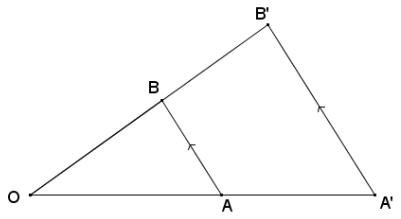
This statement corresponds to the parallel method because in the parallel method, only the endpoint A of line segment AB is dilated from center O by scale factor r to get point A’. To draw [latex]\overline{A^{\prime} B^{\prime}}\) , a line is drawn through A’ that is parallel to \(\overline{A B}\), and B’ is the intersection of that line and \(\overrightarrow{O B}\).
→ What does the parallel ⇒ ratio theorem imply about the point B’?
This implies that Do,r(B) = B’ (i.e., OB’ = r ∙ OB).
→ What does OB’ = r ∙ OB and OA’ = r ∙ OA imply about \(\overline{A B}\)?
\(\overline{A B}\) splits the sides of ∆ OA’B.
Eureka Math Geometry Module 2 Lesson 4 Problem Set Answer Key
Question 1.
Use the diagram to answer each part below.
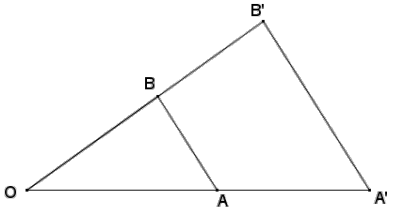
a. Measure the segments in the figure below to verify that the proportion
is true.
\(\frac{O A^{\prime}}{O A}=\frac{O B^{\prime}}{O B}\)
Answer:
Actual measurements may vary due to copying, but students should state that the proportion is true.
b. Is the proportion \(\frac{O A}{O A^{\prime}}=\frac{O B}{O B^{\prime}}\) also true? Explain algebraically.
Answer:
The proportion is also true because the reciprocals of equivalent ratios are also equivalent.
c. Is the proportion \(\frac{A A^{\prime}}{O A^{\prime}}=\frac{B B^{\prime}}{O B^{\prime}}\) also true? Explain algebraically.
Answer:
True. OA’ = OA + AA’, and OB’ = OB + BB’. So, using the equivalent ratios in part (a):
Question 2.
Given the diagram below, AB = 30, line l is parallel to \(\overline{A B}\), and the distance from \(\overline{A B}\) to l is 25. Locate point C on line l such that ∆ ABC has the greatest area. Defend your answer.
Answer:
The distance between two parallel lines is constant and in this case is 25 units. \(\overline{A B}\) serves as the base of all possible
triangles ABC. The area of a triangle is one-half the product of its base and its height. No matter where point C is located on line l, triangle ABC has a base of AB = 30 and a height (distance between the parallel lines) of 25. All possible triangles will therefore have an area of 375 units2.
Question 3.
Given ∆ XYZ, \(\overline{X Y}\) and \(\overline{Y Z}\) are partitioned into equal-length segments by the endpoints of the dashed segments as shown. What can be concluded about the diagram?
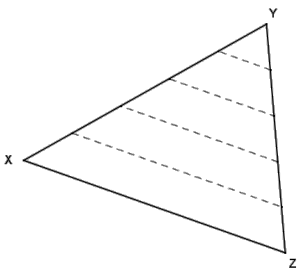
Answer:
The dashed lines joining the endpoints of the equal length segments are parallel to \(\overline{X Z}\) by the triangle side splitter theorem.
Question 4.
Given the diagram, AC = 12, AB = 6, BE = 4, m∠ACB = x°, and m∠D = x°, find CD.
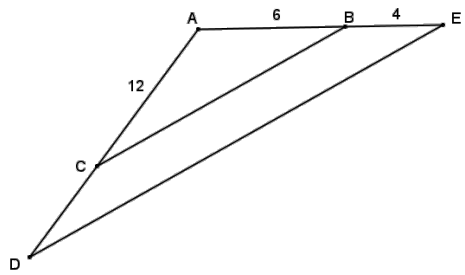
Answer:
Since ∠ACB and ∠D are corresponding angles and are both x°, It
follows that \(\overline{B C}\) || \(\overline{E D}\). By the triangle side splitter theorem \(\overline{B C}\) is a proportional side splitter so \(\frac{A C}{C D}=\frac{A B}{B E}\).
\(\frac{12}{C D}=\frac{6}{4}\)
CD = 8
Question 5.
What conclusions can be drawn from the diagram shown to the right? Explain.
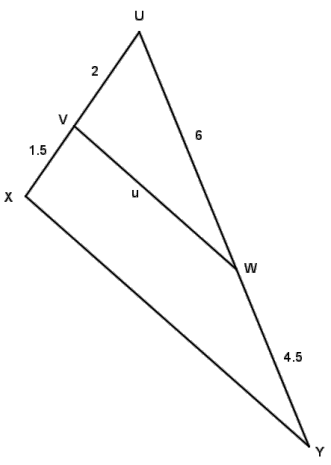
Answer:
Since \(\frac{3.5}{2}=\frac{7}{4}\) and \(\frac{10.5}{6}=\frac{7}{4}\), \(\frac{U X}{U V}=\frac{U Y}{U W}\), so the side splitter \(\overline{V W}\) is a proportional side splitter.
This provides several conclusions:
1. The side splitter \(\overline{V W}\)is parallel to the third side of the triangle by the triangle side splitter theorem.
2. ∠Y ≅ ∠UWV and ∠X ≅ ∠UVW because corresponding angles formed by parallel lines cut by a transversal are congruent.
3. ∆ UXY is a scale drawing of ∆UVW with a scale factor of \(\frac{7}{4}\).
4. XY = \(\frac{7}{4}\)u because corresponding lengths in scale drawings are proportional.
Question 6.
Parallelogram PQRS is shown. Two triangles are formed by a diagonal within the parallelogram. Identify those triangles, and explain why they are guaranteed to have the same areas.
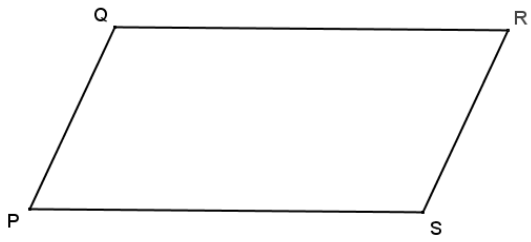
Answer:
Opposite sides oía parallelogram are parallel and have the same length, so QR = PS, and the distance between \(\overline{Q R}\) and \(\overline{P S}\) is a constant, h. Diagonal \(\overline{P R}\) forms ∆ PQR and ∆ PSR that have the same base length and the same height and, therefore, the same area.
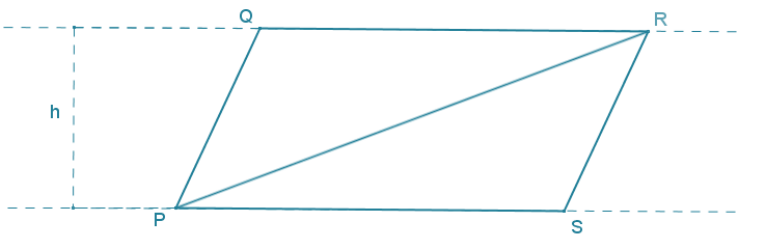
Diagonal \(\overline{Q S}\) forms ∆ PQS and ∆ RSQ that have the same base length and the same height and, therefore, the same area.
Question 7.
In the diagram to the right, HI = 36 and GJ = 42. If the ratio of the areas of the triangles is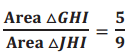 
, find JH, GH, GI, and JI.
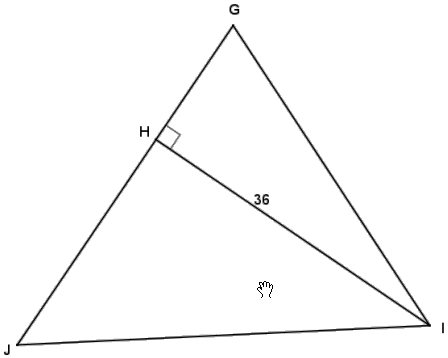
Answer:
\(\overline{H I}\) is the altitude of both triangles, so the bases of the triangles will be in the ratio of the areas of the triangles. \(\overline{G J}\) is composed of \(\overline{J H}\) and \(\overline{G H}\), so GJ = 42 =JH + GH.
\(\frac{G H}{J H}=\frac{5}{9}\)
\(\frac{G H}{42-G H}=\frac{5}{9}\)
9(GH) = 5(42 – GH)
9(GH) = 210 – 5(GH)
14(GH) = 210
GH = 15, JH = 27
By the Pythagorean theorem, JI = 45 and GI = 39.
Eureka Math Geometry Module 2 Lesson 4 Exit Ticket Answer Key
In the diagram, \(\overline{X Y}\) || \(\overline{A C}\). Use the diagram to answer the following:
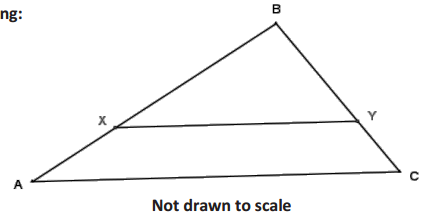
Question 1.
If BX = 4, BA = 5, and BY = 6, what is BC?
Answer:
BC = 7.5
Question 2.
If BX = 9, BA = 15, and BY = 15, what is YC?
Answer:
YC = 10