Engage NY Eureka Math Geometry Module 4 Lesson 15 Answer Key
Eureka Math Geometry Module 4 Lesson 15 Exercise Answer Key
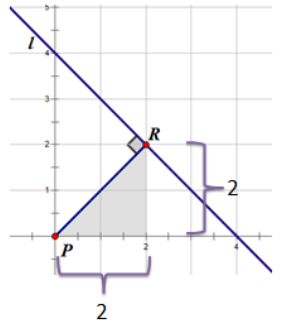
Exercise 1.
A robot is moving along the line 20x + 30y = 600. A homing beacon sits at the point (35, 40).
a. Where on this line will the robot hear the loudest ping?
Answer:
Students need to determine the equation of the line passing through the point (35, 40) that is perpendicular to the line 20x + 30y = 600. The slope of this line is –\(\frac{2}{3}\).
y – 40 = (x – 35) or y = (x – 35) + 40
There are a variety of methods available to students to use to determine the point where these two lines intersect. Using substitution is one of the more efficient methods.
20x + 30 (\(\frac{3}{2}\)(x – 35) + 40) = 600
20x + 45x – 1575 + 1200 = 600
65x = 975
x = 15
y = \(\frac{3}{2}\)(15 – 35) + 40
y = 10
The robot will be closest to the beacon when it is on the point (15, 10).
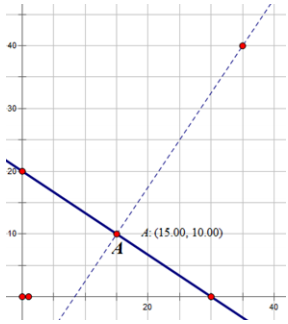
b. At this point, how far will the robot be from the beacon?
Answer:
Students need to calculate the distance between the two points B(35, 40) and A(15, 10). Encourage students to think about the right triangle that is created if one moves from A to B in two moves: one horizontal and the other vertical.
AB = \(\sqrt{(35-15)^{2}+(40-10)^{2}}\)
AB = \(\sqrt{(20)^{2}+(30)^{2}}\)
AB = \(\sqrt{1300}\) = 10√13
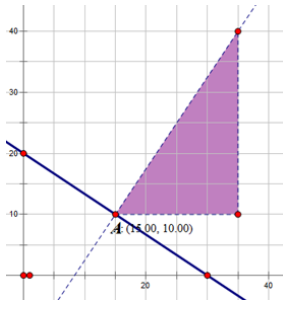
Exercise 2.
For the following problems, use the formula to calculate the distance between the point P and the line 1.
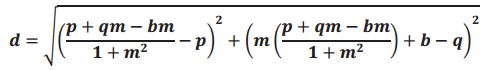
a. p(0, 0) and the line y = 10
Answer:
p = 0, q = 0, m = 0, and b = 10
d = \(\sqrt{\left(\frac{0+0-10(0)}{1+0^{2}}-0\right)^{2}+\left(0\left(\frac{0+0-10(0)}{1+0^{2}}\right)+10-0\right)^{2}}\)
d = \(\sqrt{0+(10)^{2}}\)
d = 10
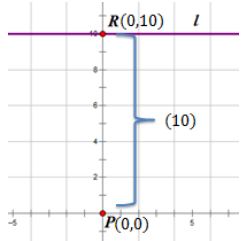
b. p(0, 0) and the line y = x + 10
Answer:
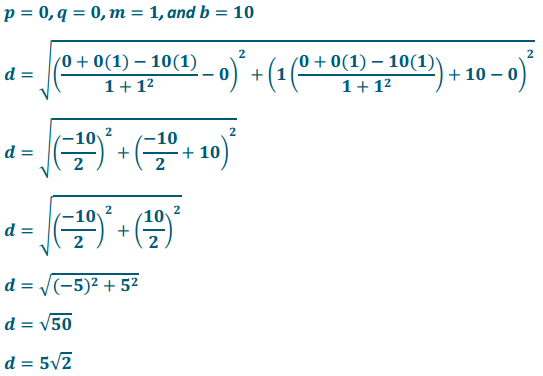
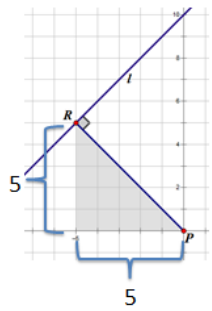
c. p(0, 0) and the line y = x – 6
Answer:
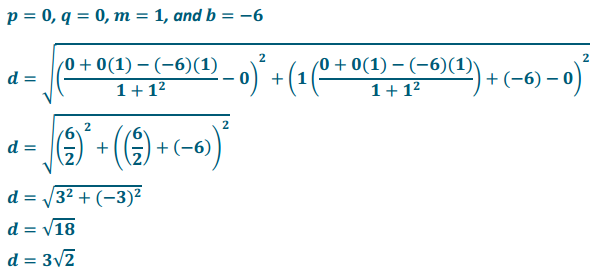
Eureka Math Geometry Module 4 Lesson 15 Problem Set Answer Key
Question 1.
Given ∆ ABC with vertices A(3, -1), B(2, 2), and C(5, 1):
a. Find the slope of the angle bisector of ∠ABC.
Answer:
The slope is – 1.
b. Prove that the bisector of ∠ABC is the perpendicular bisector of \(\overline{A C}\).
Answer:
Let \(\overline{B D}\) be the bisector of ∠ABC, where D is the point of Intersection with \(\overline{A C}\).
AB = CB = √10; therefore, ∆ ABC is isosceles, and m∠A = m∠C (base angles of isosceles have equal measures).
m∠ABD = m∠CBD by definition of angle bisector.
∆ ABD ≅ ∆ CBD byASA.
BD = CD, since corresponding sides of congruent triangles have equal lengths; therefore, \(\overline{B D}\) bisects \(\overline{A C}\).
The slope of \(\overline{B D}\) is -1; therefore, \(\overline{B D}\) ⊥ \(\overline{A C}\).
Therefore, \(\overline{B D}\) is the perpendicular bisector of \(\overline{A C}\).
c. Write the equation of the line containing \(\overline{B D}\), where point D is the point where the bisector of ∠ABC intersects \(\overline{A C}\).
Answer:
y = – x + 4
Question 2.
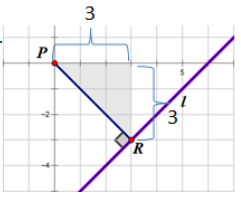
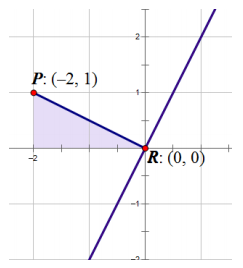
Use the distance formula from today’s lesson to find the distance between the point P(-2, 1) and the line y = 2x.
Answer:
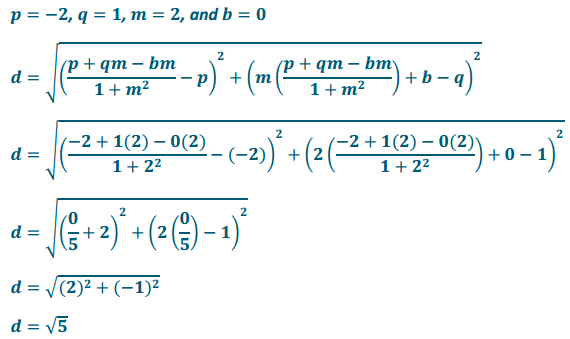
Question 3.
Confirm the results obtained in Problem 2 using another method.
Answer:
\(\overline{P R}\) is the hypotenuse of the right triangle with vertices P(-2, 1), R(0, 0), and (-2, 0). Using the Pythagorean theorem, we find that PR = \(\sqrt{2^{2}+1^{2}}\) = √5.
Question 4.
Find the perimeter of quadrilateral DEBF, shown below.
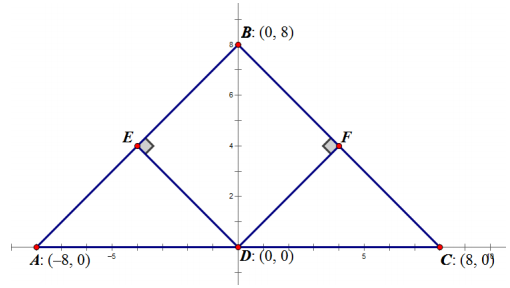
Answer:

∆ AED is a right triangle with hypotenuse \(\overline{A D}\) with length 8 and leg \(\overline{E D}\) with length 4√2. This means that ∆ AED is an isosceles right triangle (45° – 45° – 90°), which means AE = 4√2 We also know that ∆ AED ≅ ∆ DEB ≅ ∆ BFD ≅ ∆ DFC because they are all right triangles with hypotenuse of length 8 and leg of length 4√2. Therefore, the perimeter of DEBF is 4(4√2) = 16√2.
Eureka Math Geometry Module 4 Lesson 15 Exit Ticket Answer Key
Question 1.
Find the distance between the point P(0, 0) and the line y = – x + 4 using the formula from today’s lesson.
Answer:
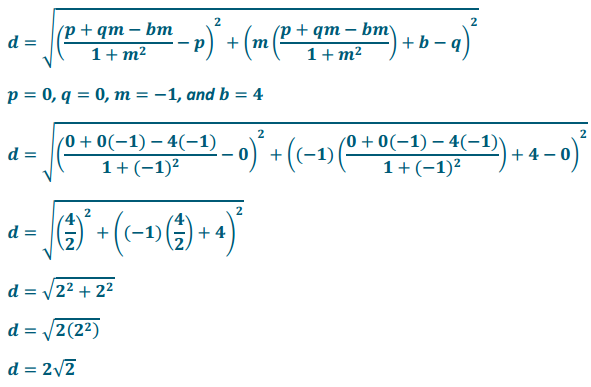
Question 2.
Verify using another method.
Answer: