Engage NY Eureka Math Geometry Module 4 Lesson 9 Answer Key
Eureka Math Geometry Module 4 Lesson 9 Example Answer Key
Consider a triangular region in the plane with vertices 0(0, 0), A(5, 2), and B(3, 4). What is the perimeter of the triangular region?
Answer:
Approximately 13.21 units
What is the area of the triangular region?
Answer:
7 square units
Find the general formula for the area of the triangle with vertices 0(0, 0), A(x1, y1), and B (x2, y2), as shown.
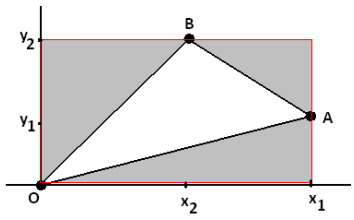
Answer:
Let students struggle with this for a while following the steps modeled above. Scaffold as necessary.
→ What is the area in square units of the rectangle enclosing the triangle?
x1 y2
→ What is the area in square units of the surrounding triangles?
Left: \(\frac{1}{2}\)
Right: \(\frac{1}{2}\)(x1 – x2) (y2 – y1)
Bottom: \(\frac{1}{2}\)(x1y1)
→ Write the general formula for the area of ∆OAB.
x1y2 – \(\frac{1}{2}\)(x2y2) – \(\frac{1}{2}\)(x1 – x2) (y2 – y1) – \(\frac{1}{2}\)(x1y1)
→ Expand the formula and simplify it.
\(\frac{1}{2}\)(x1y2 – x2y1)
Does the formula work for this triangle?
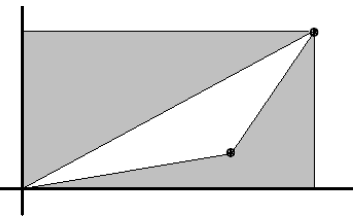
Answer:
→ Does the formula work for the triangle below?
It does, but students may get either of these formulas: \(\frac{1}{2}\)(x1y2 – x2y1) or \(\frac{1}{2}\)(x2y1 – x1y2) depending on which point they labeled (x1, y1).
These formulas differ by a minus sign. Let students compare their answer with their classmates. Make the point that the formulas depend on the choice of labeling the points but differ only by a minus sign. Students always get a positive area if they order the points counterclockwise. The method that students should follow is (1) pick a starting point; (2) walk around the figure in a counterclockwise direction doing calculations with adjacent points.
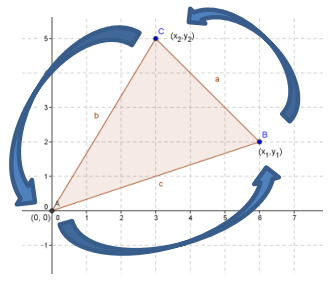
→ Do you think this formula works for any triangle with one vertex at (0, 0)? Does the quadrant matter?
Answers will vary. Yes, it always works no matter the quadrant, and the area is positive as long as (x1, y1) is the next point in a counterclockwise direction.
→ Let’s try some problems and see if our formula always works.
Eureka Math Geometry Module 4 Lesson 9 Opening Exercise Answer Key
Find the area of the shaded region.
a.
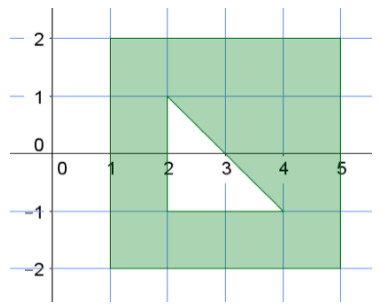
Answer:
A = 16 units2 – 2 units2 = 14 units2
b.
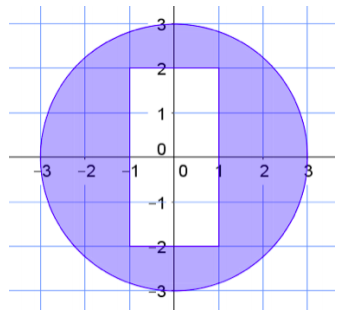
Answer:
A = 9π units2 – 8 units2 ≈ 20.26 units2
Eureka Math Geometry Module 4 Lesson 9 Exercise Answer Key
Find the area of the triangles with vertices listed, first by finding the area of the rectangle enclosing the triangle and subtracting the area of the surrounding triangles, then by using the formula \(\frac{1}{2}\)(x1y2 – x2y1).
a. 0(0, 0), A(5, 6), B(4, 1)
Answer:
9.5 square units
b. 0(0, 0), A(3, 2), B (- 2, 6)
Answer:
11 square units
c. 0(0, 0), A(5, – 3), B(- 2, 6)
Answer:
12 square units
Eureka Math Geometry Module 4 Lesson 9 Problem Set Answer Key
Question 1.
Use coordinates to compute the perimeter and area of each polygon.
a.
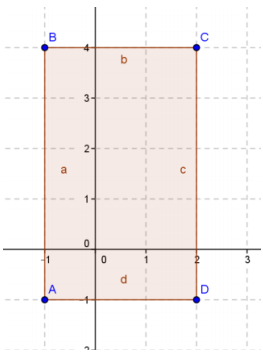
Answer:
Perimeter = 16 units
Area = 15 square units
b.
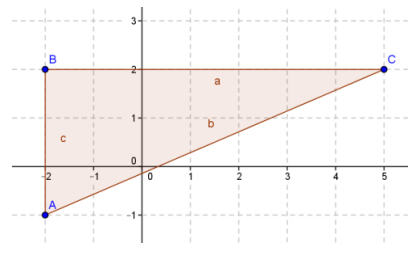
Answer:
Perimeter ≈ 17.62 units
Area = 10.5 square units
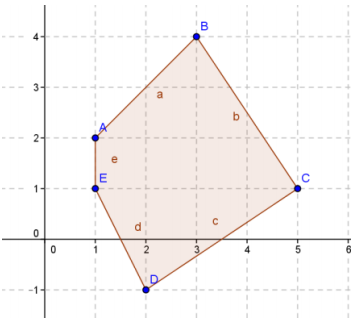
Question 2.
Given the figures below, find the area by decomposing into rectangles and triangles.
a.
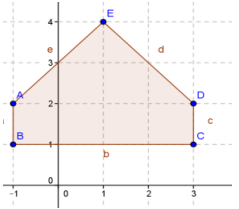
Answer:
Area = 8 square units
b.
Answer:
Area = 30 square units
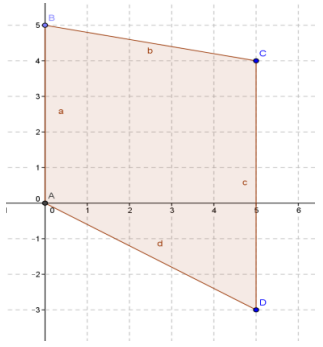
Question 3.
Challenge: Find the area by decomposing the given figure into triangles.
Answer:
11 square units
Question 4.
When using the shoelace formula to work out the area of ABC, we have some choices to make. For example, we can start at any one of the three vertices A, B, or C, and we can move either in a clockwise or counterclockwise direction. This gives six options for evaluating the formula.
Show that the shoelace formula obtained is Identical for the three options that move in a clockwise direction (A to C to B or C to B to A or B to A to C) and identical for the three options in the reverse direction. Verify that the two distinct formulas obtained differ only by a minus sign.
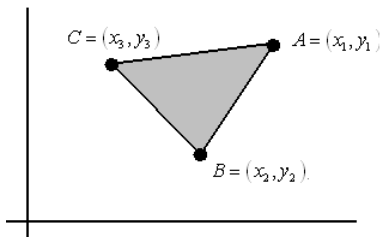
Answer:
Clockwise:
\(\frac{1}{2}\)(x1y2 + x2y3 + x3y1 – y1x2 – y2x3 – y3x1)
Counterclockwise:
\(\frac{1}{2}\)(x1y3 + x3y2 + x2y1 – y1x3 – y3x2 – y2x1)
Question 5.
Suppose two triangles share a common edge. By translating and rotating the triangles, we can assume that the common edge lies along the x-axis with one endpoint at the origin.
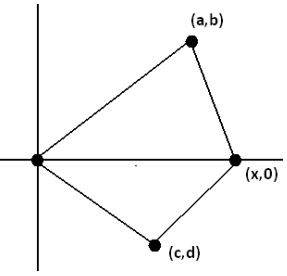
a. Show that If we evaluate the shoelace formula for each trIangle, both calculated in the same clockwise direction, then the answers are both negative.
Answer:
Top Triangle: \(\frac{1}{2}\)(0 – bx) = –\(\frac{1}{2}\)bx, where b > 0.
Bottom Triangle: \(\frac{1}{2}\)(xd – 0) = –\(\frac{1}{2}\)dx, where d < 0. Both answers are negative when calculated in the clockwise direction.
b. Show that If we evaluate them both In a counter clock wise direction, then both are positive.
Answer:
Top Triangle: \(\frac{1}{2}\)(xb – 0) = bx, where b > 0.
Bottom Triangle: \(\frac{1}{2}\)(0 – xd) = –\(\frac{1}{2}\)dx, where d < 0.
Both answers aie positive when calculated in the counterclockwise direction.
c. Explain why evaluating one in one direction and the second in the opposite direction, the two values obtained are opposite in sign.
Answer:
If two triangles share a common edge, then evaluating the shoelace formula for each triangle in a consistent direction gives answers that are the same sign; they are either each the positive areas of their respective triangles or each the negative versions of those areas.
Question 6.
A textbook has a picture of a triangle with vertices (3, 6) and (5, 2). Something happened in printing the book, and the coordinates of the third vertex are listed as ![]() . The answers in the back of the book give the area of the triangle as 6 square units.
. The answers in the back of the book give the area of the triangle as 6 square units.
a. What is the y-coordinate of the third vertex?
Answer:
8
b. What if both coordinates were missing, but the area was known? Could you use algebra to find the third coordinate? Explain.
Answer:
No, you would have an equation with two variables, so you could not solve for both algebraically unless you had a second equation with the same unknowns.
Eureka Math Geometry Module 4 Lesson 9 Exit Ticket Answer Key
Given the triangle below with vertices A(4, 3), B(-2, 3), and C(-1, -2).
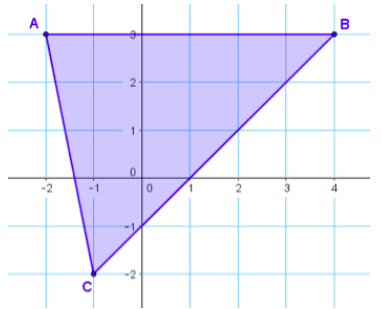
Azha calculated the area using 5 ∙ 6 – \(\frac{1}{2}\)(5 ∙ 1) – \(\frac{1}{2}\)(5 ∙ 5),
while Carson calculated the area using \(\frac{1}{2}\)(4 ∙ 3 + (-2) ∙ (-2) + (-1) ∙ 3 – 3 (-2) – 3 ∙ (-1) – (-2) ∙ 4).
Explain the method each one used.
Answer:
Azha used the decomposition method. She first determined that the area of the rectangle around the triangle is 5 ∙ 6, and then she subtracted the area of the 3 right triangles surrounding the region. Carson used the “shoelace” method that we learned in this lesson.
